基于行人位置预测的人车转向避撞路径规划*
2021-07-05李彩霞卢少波张博涵吴文娟陆嘉峰
李彩霞,卢少波,2,张博涵,吴文娟,陆嘉峰
(1.重庆大学汽车工程学院,重庆 400040;2.重庆大学,机械传动国家重点实验室,重庆 400040)
前言
《2015年全球道路安全现状报告》显示:我国行人伤亡人数约占总交通事故伤亡人数的20%,而行人过街时的伤亡人数占50%以上[1]。尤其在无信号灯、无人行横道指引的情况下,行人不遵守交通规则违规过街,导致碰撞事故发生的情况屡见不鲜。因此,在自动驾驶研究中,行人违规过街的人车避撞问题受到了广泛关注[2]。
路径规划是解决人车避撞问题的关键技术之一。常用的路径规划方法有很多,如人工势场法、基于图搜索的方法、基于采样和基于离散优化的方法等[3],但各有优劣。其中,人工势场法具有计算简单、生成的路径较平滑、实时性较好等优点,在路径规划方面得到了广泛应用。
人工势场法由Khatib[4]在1986年提出,其基本思想是在一个虚拟势场中,被控对象受到障碍物产生的斥力和目标点产生的引力,在两者合力作用下向目标位置前进。人工势场法最初应用在机器人路径规划[5],而智能车可以看作一种轮式机器人,因此可采用人工势场法为车辆规划路径。任玥等[6]根据两车纵横向相对位置构建斥力场函数,并基于模型预测控制理论建立车辆转向避撞优化目标函数,为车辆规划最优避撞路线。徐杨等[7]考虑两车纵向距离分别构建车辆前后方势场,且为构建车辆的侧向势场,在其纵向势场的基础上采用类高斯函数来计算车辆的整体势场,并将行车环境势场引入到模型预测控制目标函数中,以实现轨迹规划与跟踪的统一建模,为车辆提供安全路径。Hu等[8]根据自车与前车纵向相对距离确定障碍物速度势场,当两车纵向相对距离过小时,障碍物速度势场系数为1,否则为0。并选取一定的纵横向影响距离构建障碍物势场,为车辆规划转向避撞路径。然而,这些研究在构建势场时,未考虑车辆转向避撞需要的纵向距离lx与车辆实际避撞需要侧向距离ly的关系,当车辆和障碍物的相对位置不同时,ly不同,则lx也不同。所以,需要考虑两者之间的关系为车辆规划避撞路径,保证车辆有足够的纵横向避撞距离。
当避撞对象为行人时,就须考虑行人过街时的运动特性。Keller等[9]提出了一种集多传感器融合、车辆态势分析、决策和控制于一体的新型主动行人安全系统。通过行人检测技术实时检测行人位置,并采用七次多项式为车辆规划避撞路径。Zhuang等[10]根据行人运动状态确定行人位置,并以车辆对行人造成的威胁程度、行人位置及过街群体大小为因素评估当前危险程度,基于行人感知风险建立行人速度函数,确定行人运动速度。Iryo⁃Asano等[11]考虑过街信号灯情况、人行道位置等分析行人过街时速度变化情况,并建立行人速度突变模型,每0.5 s分析一次行人的位置和速度,以计算行人加减速的概率。上述研究大多针对有信号灯和人行横道的过街场景,重点考虑行人运动速度的变化情况,而对无信号灯且无人行横道的情况考虑不足,由于没有规范信号的指引,行人的运动具有较大的不确定性,驾驶员也难以及时做出准确判断,相对于合规的过街场景,该场景更容易导致交通事故。
因此,本文中主要针对无信号灯、无人行横道的行人过街情况,考虑行人过街的方向不确定性,建立行人过街方向概率模型,并以此预测行人位置。在人车避撞时,采用了改进人工势场法,提出了基于人车相对位置实时调节的可变长轴椭圆障碍物势场,在制动避撞无效而转向避撞可行的情况下,为车辆规划避撞路径。
1 行人位置预测与车辆安全距离
车辆正常行驶时,如果前方有行人出现,车辆就需要根据实际情况进行避撞操作。考虑到行人过街方向的不确定性,建立行人过街方向概率模型及行人位置预测模型,并建立车辆转向避撞安全距离模型。
1.1 行人过街方向概率模型
图1为人车避撞场景示意图。红色车辆为被控车辆,车速为vc,过车辆起始点处质心作垂直于道路中线的垂线,以该线与道路中线形成的交点为原点o,以车辆行驶方向为x轴正向,以指向被控车辆的方向为y轴正向,建立大地坐标系描述车辆和行人的运动状态。假设行人以速度vp匀速过街,道路为单向行驶双车道,车辆匀速行驶且邻车道可用。
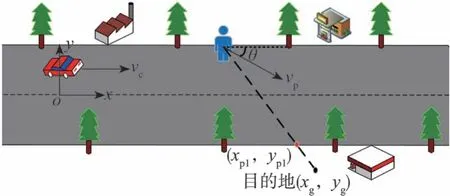
图1 人车避撞场景
行人可以自由选择过街方向,每一个过街方向都会给行人带来不同的过街收益。本文中采用效用函数来衡量不同过街方向下行人的过街收益,效用越大行人过街收益越大,则行人选择该方向的概率越大。鉴于行人选择过街方向时会受到环境因素的影响,故考虑横穿过街长度最短及距离目的地最近两种情况,建立行人过街效用函数。
不同的过街方向决定了不同的过街长度,在相同速度情况下,行人需要的过街长度越长,过街时间则越长,行人得到的效用便越低,故考虑横穿过街长度建立行人过街效用函数为

式中:θ为车辆前进方向和行人前进方向的夹角,考虑行人不会过远偏离垂直过街方向,取θ∈(30°,150°);θ=30°或150°时,λ1为行人横穿过街最长距离,取λ1=16 m;Wr为道路总宽度,取8 m。
在允许的情况下,行人会根据目的地所在位置选择前进方向,以期距离目的地更近[12]。其实际行进方向与行人和终点连线的夹角越小,行人便可以越快到达目的地,即行人得到的效用越大,故建立以目的地为导向的行人效用函数为

式中:λ2为行人到达目的地最长距离,参照λ1大小,近似取λ2=20 m;如图1所示,(xg,yg)为目标点坐标;(xp1,yp1)为行人走到另一边道路边界时的坐标;xp(0)为行人运动初始位置的x坐标。
则行人选择各运动方向的总效用函数E为

式中α为权重系数,假设行人偏向于选择以目的地为导向的方向,故取α=0.4。
在行人过街效用函数基础上,建立行人巢式logit(NL)模型[13],将行人朝向的(30°,150°)扇形区域按角度均分为121份,即为121个虚拟选择肢。Ei(i=1,2,…,121)为每一选择肢的效用项,则选择肢i的选择概率为

式中m为调节系数,可根据仿真结果确定。
假设行人起始点为(50,4),目标位置为(45,-5)。根据NL模型可得行人过街选择各方向的概率,如图2所示。可见,行人选择θ=100°的概率最大,即此时行人过街所得效用最大。

图2 行人过街方向概率分布
1.2 动态行人位置预测模型
因为行人具有运动不确定性,所以在实际驾驶过程中,动态行人是最难处理的避撞对象之一。若充分考虑行人的静止和运动状态,根据行人当前状态预测行人未来时刻的位置,由每一时刻的行人位置生成行人过街路径,则可以提前判断两者是否有可能碰撞,从而使车辆提前进行避撞操作,提高避撞成功率。
为真实反映行人横穿马路的随机性,在考虑行人过街速度[14]的基础上,进一步考虑行人的运动方向,建立的行人纵横向速度模型为

式中:vp为行人过街速度;vpx、vpy分别为行人速度在纵横向的分量;θ由行人过街方向概率模型确定。
为简化研究,假设行人方向选择在出发时根据交通情况一次性确定,则行人位置可由下式表示:

式中:yp(0)为行人运动初始位置y坐标;(xp(t),yp(t))为t时刻的行人预测位置;当行人初始位置位于车辆偏左区域过街时,其横坐标减小,即yp(t)减小,反之增大;时间t取值范围为:0≤t≤Tcp,Tcp表示预测行人未来位置的时间上限值,取车辆和行人纵坐标相等即在当前运动情况下,两者最可能发生碰撞的时间为Tcp,即

式中vc为纵向车速。
1.3 转向避撞安全距离模型
车辆避撞的方式较多,如制动、转向及制动加转向等,文中重点关注行人过街的方向不确定性,仅考虑转向避撞方式。且李霖等[15]通过对比转向和制动避撞的临界TTC(time⁃to⁃collision)值,发现转向避撞在某些工况下比制动避撞更有优势,所以在某些制动不可避撞的情况下,可以采用转向避撞。
彭涛等[16]将转向避撞分为定半径转向和直线段换道两种耦合运动,提出车辆避撞安全距离模型。该模型是在制动无法成功避撞但转向还可以避撞的情况下,计算出车辆最晚开始实施转向避撞所需纵向避撞距离。避撞安全距离的选取直接影响行车安全、乘车舒适性和道路通行效率,是自车判断是否需要采取转向避撞措施的重要依据。研究表明[17],车辆转向避撞安全距离与车速、车辆侧向加速度及需要的侧向位移等因素有关,且随着纵向车速变大而增加。当车辆避撞需要的侧向位移较大时,其预留的纵向距离较大,驾驶员往往会更早地进行转向操作,以确保在安全的前提下,减少不舒适感,即需要根据每一时刻的车速、车辆侧向加速度和其需要的侧向位移来计算车辆成功转向避撞的临界距离,避撞安全距离模型[18]表示为

式中:Sx为车辆避撞纵向安全距离;ay为车辆侧向加速度;Sy为车辆避撞所需侧向位移,与车辆和行人的相对位置有关。当车辆行驶路径与行人安全区域无重叠时,两者无碰撞危险,车辆所需侧向位移为零,无需转向。当行人位于车辆行驶中心线时,危险程度最高,车辆需要的侧向位移最大;随着行人偏离车辆行驶中心线,危险程度下降,Sy逐渐减小。所以,通过计算车辆左右转向避撞时需要的侧向位移可以选择转向方向,考虑到乘坐舒适性和避撞成功可能性,优先选择Sy较小的一方进行转向避撞。故车辆需要的侧向位移Sy为
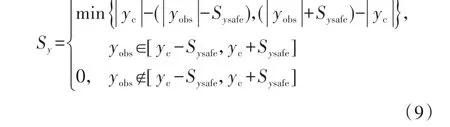
式中:yobs为障碍物横坐标;yc为车辆横坐标;Sysafe为考虑行人和自车宽度的临界侧向安全距离。
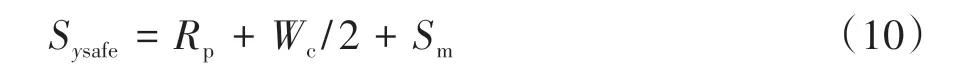
式中:Rp为行人半径;Wc为车辆宽度;Sm为两者侧向安全距离裕值。
2 考虑行人路径的人工势场
为使规划出来的路径成功避撞,结合上述分析的行人过街路径,构建引力及斥力势场,并对障碍物势场进行改进,使其长轴可以根据行人位置实时变化。
2.1 道路中心线及方向引力势场
传统人工势场法一般以固定点为目标,而对于车辆来说,目标点起着引导车辆行驶的作用,所以其目标不会是静止不动的点。而实际中,车辆主要沿车道中线行驶,故将行驶车道中心线设为横向目标位置,则中心线势场函数[19]为

式中:Kcenter为道路中心线势场调节系数;yr,i为第i条车道中心线纵坐标(i=l,r,分别表示左、右车道)。图3(a)所示为左车道中心线势场。

图3 道路中心线及方向引力势场
方向引力势场引导着车辆向前行驶,在车辆起始点处势场值最大,随着远离起始点,引力势场逐渐变小,以使车辆沿着势场下降的方向到达目标位置,其函数表达式[20]为

式中:Katt为方向引力势场调节系数,决定势场的下降速度。方向引力势场如图3(b)所示。
2.2 道路边界及车道线斥力势场
道路边界势场对车辆产生斥力,以防止其驶离道路。在该势场中,道路边缘处的势场值最大,之后势场值迅速下降,形成中间低两边高的势场分布,以保证车辆在道路上正常行驶,采用的道路边界势场函数[21]为
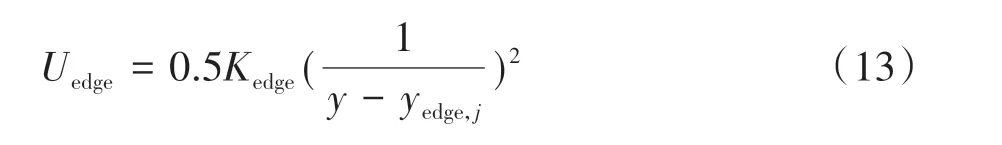
式中:Kedge为道路边界势场调节系数;yedge,j为第j条道路边界线的纵坐标。道路边界势场如图4(a)所示。
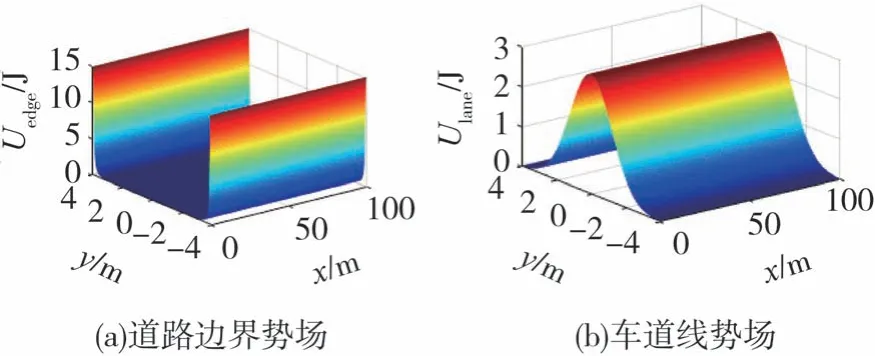
图4 道路边界及车道线势场
为避免车辆不必要的变道,构造了车道线势场函数。该势场不仅可以生成变道障碍,且可以引导车辆沿自车道行驶。车道线势场值一般较小,以便车辆遇到障碍物时可以容易克服该势场产生的阻力,安全变道。根据上述对车道线势场的功能分析,采用类高斯函数[21]建立车道线势场,故车道线势场函数为

式中:Klane为车道线势场调节系数;yc为车道线纵坐标;σ与车道宽度有关,决定了车道线势场的下降速度。车道线势场如图4(b)所示。
2.3 可变障碍物椭圆斥力势场
障碍物势场的建立,可以保证被控车辆与过街行人保持相对安全的状态。在传统人工势场法中,障碍物斥力势场以障碍物为圆心,障碍物影响距离为半径,生成圆形斥力作用范围,以保证被控对象安全避开障碍物。
而对于车辆而言,传统的圆形障碍物势场已经无法适用于其转向避撞的场景。这是因为车辆在转向避撞时,纵向速度远大于横向速度,导致纵向避撞距离远大于横向避撞距离,所以纵横向区域的危险程度分布不相同,因此将障碍物圆形斥力势场改进为椭圆形斥力势场,如图5所示,以车辆实际行驶方向即纵向为长半轴σx,其垂直方向为短半轴σy。

图5 障碍物椭圆斥力势场
纵向斥力势场作用范围较大,以满足车辆对较大纵向避撞距离的需求;而横向斥力势场作用范围较小,以便在满足横向安全的同时使车辆尽快驶出斥力势场作用范围,正常行驶。采用二维高斯分布函数[8]生成障碍物椭圆斥力势场,势场函数表达式为

式中:Kobs为障碍物斥力势场的调节系数;xobs、yobs分别为障碍物纵横向坐标。图6(a)为行人坐标(50,3)时的障碍物三维势场,σx为18.78 m,σy为1.83 m,图6(b)为障碍物势场俯视图。

图6 障碍物斥力势场
椭圆长半轴σx由车辆避撞安全距离决定,可以根据车辆及行人的运动状态实时变化。当车辆转向避撞时,存在最小转向安全距离,该距离与车辆避撞需要的侧向位移有关。当由两者相对位置计算出车辆避撞需要的侧向位移较大时,其安全距离也应增大,故障碍物斥力势场椭圆长轴也应增大,以保证安全。因此,取车辆避撞安全距离Sx为椭圆长半轴,如式(8)所示。
椭圆短半轴σy的取值与行人半径、车辆宽度、两者侧向安全裕值有关。且因为车辆侧向避撞距离随短轴增加而增加,所以椭圆短轴应在保证安全的基础上尽可能小,以减少车辆避撞需要的侧向距离,尽可能减小乘坐不舒适性,故取椭圆短轴为人车侧向安全距离Sysafe,如式(10)所示。
3 仿真验证与分析
考虑到静态行人和动态行人过街状态的不同,分别建立静态和动态避撞场景,为车辆规划避撞路径,并对其避撞可行性进行分析。
3.1 仿真场景与参数
假设道路为单向行驶双车道直路,单车道宽4 m,自车沿着车道中线匀速行驶,车速为25 m/s。行人匀速过街,速度为1.25 m/s,行人半径取为0.3 m。
根据行人过街方向不同,分别设置了行人静止,θ=30°、90°和150°的避撞场景1~4,具体数据如表1所示。在相同避撞场景下,设置了障碍物椭圆长半轴固定为15 m的对比路径规划方法,以验证改进的可变椭圆长轴势场路径规划方法的有效性。
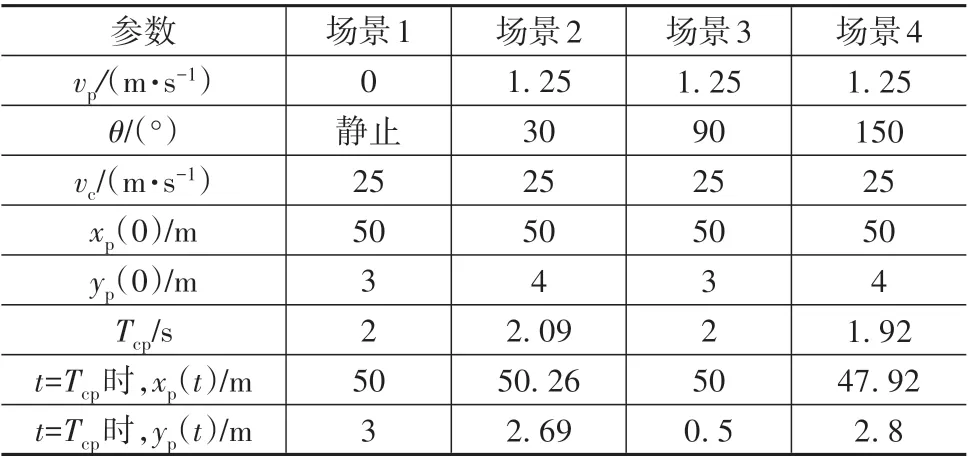
表1 路径规划主要参数
3.2 避撞路径效果对比
行人在各个避撞场景下,由初始位置向目的地行进,若车辆保持原路径行驶,将在Tcp时刻与行人发生碰撞。所以,在改进势场作用下,车辆将沿着势场梯度下降最快方向行驶,进行转向避撞操作。图7~图10为两种势场规划的避障路径结果,分别对应着场景1~场景4。其中,黑色实线为改进后人工势场(IAPF)的规划路径,红色虚线为长轴固定人工势场(APF)的规划路径。

图7 行人静止时的规划路径
表2为改进前后各场景下对应的障碍物势场长半轴数据。其中,场景1、场景2和场景4中,计算出的可变长半轴数值大于固定长半轴数值,所以与之对应的图7、图8和图10中,采用改进的可变长半轴势场规划的路径避撞操作开始较早。而场景3中的可变长半轴小于固定长半轴,所以与之对应的图9中,可变长半轴势场中避撞操作较晚,且车辆转向避撞过程中,行人已从车辆一侧穿到另一侧,此时车辆左前方势场值较小,所以车辆选择左转避撞。
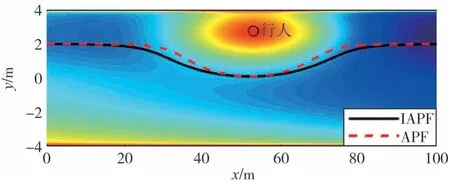
图8 θ=30°时的规划路径

图9 θ=90°时的规划路径

图10 θ=150°时的规划路径

表2 各场景长半轴数值
由图可知,改进后的障碍物势场长轴可以根据当前避撞场景实时变化,所以改进后势场的规划路径平滑性较好。为比较两种势场规划路径的平滑性,分别计算了两种方法规划的路径在各位置的曲率,图11(a)~图11(d)分别为场景1~4所对应路径的曲率,其中红色虚线代表改进前长轴固定势场(APF)规划路径的曲率,黑色实线代表改进后长轴可变势场(IAPF)规划路径的曲率。

图11 改进前后避撞路径曲率对比
整体而言,与改进前路径相比,改进后的路径曲率较小,所以路径更平滑。在图11(a)、图11(b)、图11(d)中,改进后的路径曲率变化较平缓,且其最大值小于改进前曲率最大值,故其规划的路径平滑性较好。对于车辆来说,改进后的路径可跟踪性更高,乘车舒适性也较高。图11(c)中,改进后的路径曲率稍大于改进前路径曲率,这是因为此避撞场景下车辆需要的侧向避撞距离很小,所以改进后势场长半轴小于改进前势场长半轴,为车辆提供的转向避撞距离较小,但可以保证安全避撞。这就说明改进后的路径在保证安全的基础上,减小了换道避撞距离。
3.3 改进路径的避撞可行性分析
在分析改进后规划路径的避撞可行性时,为更清楚地表示行人及车辆的运动状态,以红色封闭五边形代表间隔一定时间内9个时刻的自车位置,图形尖端表示行车方向,实线绿色圆形表示行人在对应时刻的位置。在同一时刻下的车辆和行人用线段连接,并对其编号,以便观察整个过程中两者的相对位置情况。由于横纵坐标轴单位长度表示距离不同,所以车辆宽度较短,行人外形显示为椭圆形。
图12~图15分别为上述4种避撞场景的路径可行性分析。由车辆转向避撞轨迹可见,在各对应时刻车辆始终在道路行驶,未超出道路边界,满足基本的行驶安全需求。且每种避撞场景下车辆和行人的相对距离都呈现出先减小后增加的趋势,在时刻5时车辆和行人的相对距离最小,但两者始终保持一定的安全距离未发生碰撞。故可证明,本文改进的路径规划方法可以避开静态和动态过街行人,满足人车安全需求。
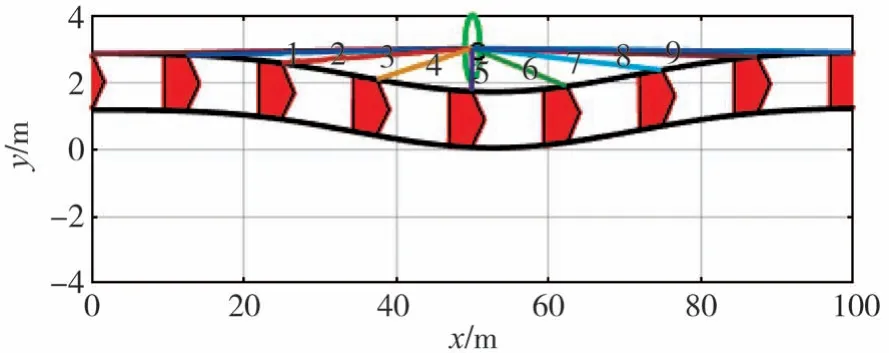
图12 行人静止时的路径分析

图13 θ=30°的路径分析
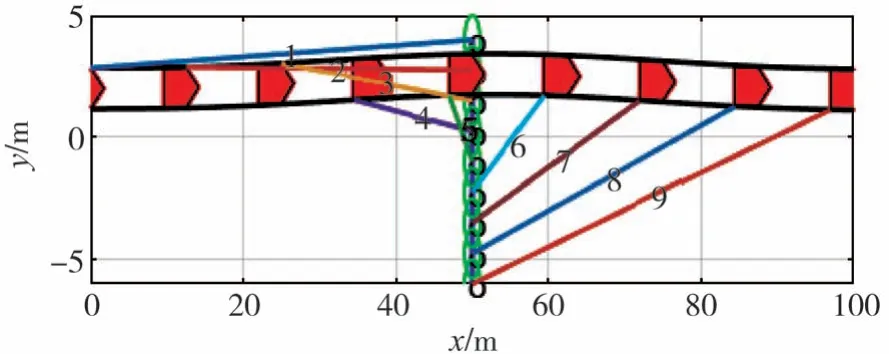
图14 θ=90°的路径分析
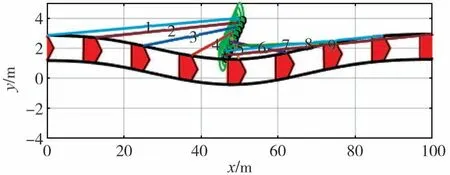
图15 θ=150°的路径分析
4 结论
(1)通过建立效用函数,分析行人选择各过街方向的概率分布,确定行人前进方向。建立了考虑行人前进方向的位置预测模型,可以根据行人当前运动情况预测未来时刻的行人位置。
(2)提出一种基于纵横向避撞安全距离的椭圆形长轴自适应变化的改进人工势场,以适应具有行为随机性的动态行人避撞路径规划需求。
(3)与改进前人工势场相比,改进后的人工势场可以实时计算障碍物椭圆长轴大小,为车辆规划避撞路径,且规划的路径平滑性更好,实用性更强。
