融合TangentBug与Dubins曲线的智能轮式车辆局部路径规划算法*

张旭东，徐福康，邹 渊，郭宁远，张 宇

（1.北京理工大学，北京 100081；2.陆军装甲兵学院，北京 100072）

前言

随着汽车智能化的发展，自动驾驶技术成为智能车辆领域研究的重要方向，而路径规划是其关键技术之一。智能车辆的路径规划是指在一定环境模型的基础上，给定起点与目标点后，按照性能指标规划出一条无碰撞、能安全到达目标点的有效路径［1］。

目前路径规划按不同算法可分为图搜索类算法［2-3］、采样类算法［4-5］、人工势场类算法［6-8］和智能仿生类算法［9-10］等。图搜索和采样类算法最为常见，运算速度较快，但需要路径平滑处理以适应车辆的运动特性，并常用于已知全局地图的情况。人工势场类算法对障碍物的适应性较好，但容易陷入局部最优解。智能仿生类算法参考了生物的行为模式和特性，相比其他算法可以得出更优的结果，其中Lumelsky等［11］参考爬虫（Bug）的行为模式，针对仅能获取局部地图和定位信息的情况，提出了具有完备性的Bug1和Bug2算法。

Bug1和Bug2面向可全向运动的机器人，解决其在二维平面上的局部路径规划问题，要求机器人装有接触式传感器以探测周围障碍物，并有精确的实时定位。Bug1和Bug2均由朝目标移动和环绕障碍物两种状态组成，但Bug2在简单场景下规划路径的总长度可能更短，而在复杂场景时Bug1更为稳健。Sankaranarayanan等［12］修改了Bug2中环绕障碍物的规则，提出了在某些场景下规划路径总长度更短的Alg1算法。Kamon等［13］使用测距传感器解决了Bug类算法必须接触障碍物的问题，并提出了基于局部切线图的TangentBug算法，其规划路径的总长度随测距传感器探测距离的增加而减小。Kim等［14］在TangentBug的基础上考虑了采用Ackermann转向的车辆存在最小转向半径的运动约束，其规划路径为预瞄算法生成的圆弧而非直线段，但路径的曲率变化较大，不利于路径跟随控制。Xu等［15］在小尺度未知环境范围内将Dubins曲线和Bug类算法思想结合，但由于中间位姿与目标点的位姿相关，其仿真结果中的规划路径出现了扭结和圆环。为保证规划路径的安全性，文献［14］和文献［15］中基于局部切线图对障碍物边界点进行扩展的方法，在实际应用中易受传感器精度的制约和环境的干扰，扩展距离往往过于保守。此外，上述算法均要求被控对象有精确的实时定位，而算法的收敛性易受定位误差的影响。

针对现有研究存在的不足，本文中面向采用Ackermann转向的智能轮式车辆，提出了一种融合TangentBug与Dubins曲线的局部路径规划算法。首先通过采样法构建规划参考点集合，然后在TangentBug算法框架下生成Dubins曲线作为规划路径，旨在满足车辆最小转向半径和目标点的航向要求，并加入了碰撞检测和考虑定位误差的状态转换规则，最后通过实车实验，验证了本文所提出算法的可行性。

1 车辆运动学建模

对于采用Ackermann转向的车辆，其运动学模型如图1所示［16］。在惯性坐标系OXY下，车辆后轴中心的坐标为（Xr，Yr），车辆的横摆角为Ψ，点C为车辆在转向过程中的瞬时转动中心，车辆后轴中心速度为v，前轮偏角为δ，车辆轴距为lw，车辆后轮的转向半径为r。以车辆坐标和横摆角为状态量q=［Xr，Yr，Ψ］T，以车速和横摆角速度为控制量u=［v，ω］T，可得车辆的运动学模型如式（1）所示。

图1 车辆运动学模型

转向半径与前轮偏角的关系如式（2）所示。当前轮偏角为最大值δmax时，有最小转向半径rmin。

2 局部路径规划算法设计

本文算法与自动驾驶系统结合的框架如图2所示。本文算法对应“局部路径规划”模块，其输入为环境感知模块的输出信息，包括障碍物信息和车辆及目标位姿，其输出为参考路径，并作为运动控制模块的输入。局部路径规划模块包含环境建模和决策规划两层，环境建模层用于接收障碍物信息以构建规划参考点集合和局部地图，之后决策规划层利用上述信息结合车辆自身和目标的位姿生成参考路径。

图2 自动驾驶系统框架图

2.1 基于采样的规划参考点集合构建

假设在二维平面R2上有一点P，其状态q=［X，Y，Ψ］T，以此构建如图3所示的车辆坐标系oxy，其中点P与点o重合。对于可以在任意方向上获取障碍物距离信息的测距传感器，在状态q和方位角φ上获得的最近障碍物距离ρ（q，φ）可用式（3）表示。

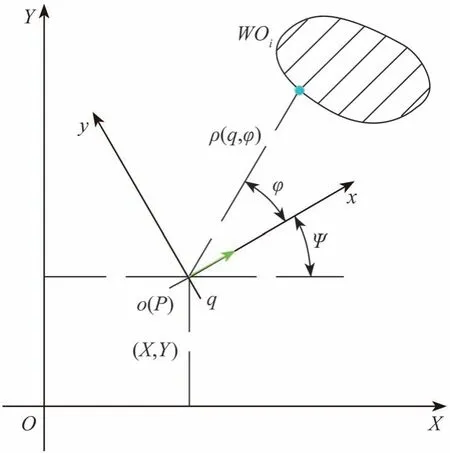
图3 车辆坐标系与障碍物信息

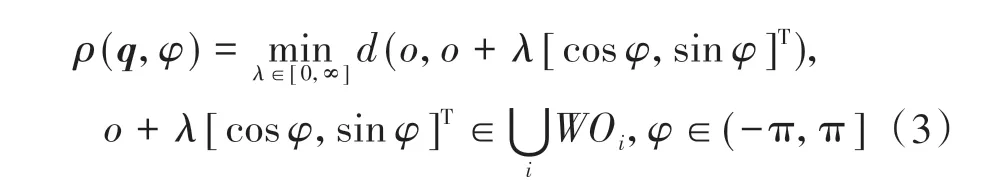
式中:d（a，b）为点a与点b在二维平面上的欧氏距离；λ为比例系数，取值范围在［0，∞］，λ[cosφ，sinφ]T表示模长为λ、辐角为φ的向量；WOi表示第i个障碍物。

在实际应用中，由于测距传感器存在角度分辨率φr，故方位角φ是离散的而非连续的，离散的角度用φn表示，此外还受最大探测距离ρmax的限制。因此重新定义测距传感器在不同方向上获取的距离ρr（q，φn），如式（4）所示。

式中atan2（a，b）表示点a相对于点b的方位角。

对于没有障碍物遮挡，位于测距传感器探测边界的点b，定义其构成的集合B为

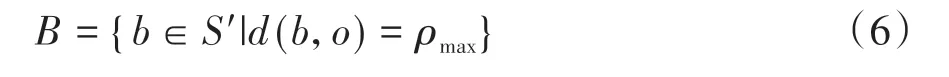
在障碍物的边界附近，距离ρr（q，φn）会发生较大的变化，因此通过对sn相邻点的距离进行分析，可得到不同类型的障碍物边界点。对于障碍物边界点的旋转采样，可分为顺时针和逆时针采样两种情况。如图4所示，点O1为顺时针采样的边界点，点O2为逆时针采样的边界点。对于集合S中的任意一点sn，令sn-1，sn-2，...，sn-m表示该点顺时针方向上相邻的m个点，令sn+1，sn+2，...，sn+m表示该点逆时针方向上相邻的m个点。设用于障碍物边界点判断的距离阈值为de，Ecw为顺时针采样的边界点集合，Eccw为逆时针采样的边界点集合，那么Ecw和Eccw可分别用式（7）和式（8）表示。

图4 障碍物边界点的旋转采样

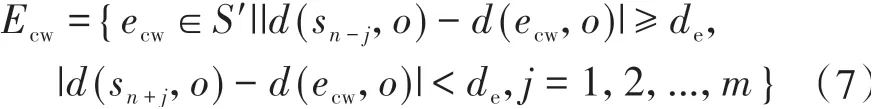
式中:ksafe为安全系数；rsafe为安全距离。

然后确定旋转角度的上限θsample，这里令θsample=ksampleθsafe，ksample为采样比例系数。采样的步长取为传感器的角度分辨率φr，那么逆时针旋转采样点的集合E′ccw为

同理可得顺时针旋转采样点的集合E′cw为

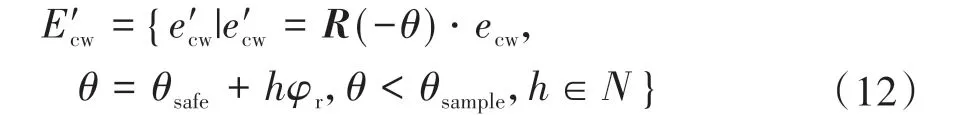
在本文的规划算法中，作为规划参考的点有3种:一是不受障碍物遮挡，位于测距传感器探测边界上的点；二是基于障碍物边界点旋转采样后的点；三是目标点T。对于集合T′，若T位于传感器探测范围内，则T′=｛T｝，否则T′=Ø。当考虑全部方向时，设规划参考点的集合为F，则

若仅考虑自身前方信息，设规划参考点的集合为F′，则

2.2 沿规划路径的碰撞检测

本文算法通过沿规划出的Dubins曲线进行严格的碰撞检测以保证规划路径的安全性。对存在最小转向半径且不能后退的车辆，在朝各个方向运动时的最短路径可用Dubins曲线表示［17］。与圆弧路径相比，Dubins曲线在满足目标点的航向要求的情况下，使规划路径最短。

如图5所示，采用覆盖圆将车辆包围，其圆心分别位于车辆中心，前轴中心和后轴中心，覆盖圆的半径为rsafe。若任意覆盖圆内存在障碍物，则认为存在碰撞的风险。从Dubins曲线起点S开始，沿曲线以固定步长选取车辆位置参考点，该参考点与车辆后轴中心点重合，参考点处切向量的方向为车辆的航向。若从规划出的Dubins曲线的起点到终点均通过了碰撞检测，那么认为该规划路径是安全的，否则认为有碰撞的风险。

图5 沿规划路径进行碰撞检测

2.3 决策规划算法

本文的局部路径规划算法基于以下假设:车辆和障碍物均位于二维平面上；障碍物的数量和周长有限；车辆配有测距传感器，可比较准确地获取探测范围内各个方向上障碍物的距离；车辆配有定位系统，可比较准确地定位；目标的位姿已知；车辆只能向前移动；车辆采用Ackermann转向。

本文的局部路径规划以TangentBug算法为基本框架，同样由朝目标移动和环绕障碍物两种状态组成，以保证本文算法的完备性。但本文算法在生成参考路径时借助规划参考点集合，生成了Dubins曲线以代替TangentBug中的直线并考虑了其安全性，在处理状态转换规则和判断目标点是否可到达时考虑了定位系统的误差，且无须提前规定环绕障碍物的方向。局部路径规划算法的伪代码如表1所示，其中:unreachable为判断目标点是否可以到达的旗标，初始化时令unreachable=false；ld为生成的Dubins曲线长度，dt为距离阈值，若规划参考点为目标点且ld＜dt，即认为车辆到达目标点附近，dt的取值可根据车辆的几何尺寸或实际需要设定；d′（P，T）用于记录车辆与目标点的距离。

表1 局部路径规划算法

2.3.1 朝目标移动状态

朝目标移动状态算法的伪代码如表2所示。其中state为状态旗标，若state=“motion toward the target”，车辆则处于朝目标移动的状态，state初始化为此值。若state=“boundary following”，车辆则处于环绕障碍物的状态。

表2 朝目标移动状态算法

在朝目标移动状态时，设目标点T在车辆坐标系下为点t，集合F中任意元素fi的代价cfi为车辆自身到该元素的距离加该元素到目标点的欧式距离，即

按代价由小到大的顺序，依次生成Dubins曲线并进行碰撞检测，一旦通过碰撞检测，则以此Dubins曲线作为局部参考路径，否则认为没有安全的路径并停车。如图6所示，在车辆坐标系oxy下，Dubins曲线的起点在原点o处，其状态可表示为:qo=［0，0，0］T。对于集合F中的元素fi，其在车辆坐标系下的坐标为（xfi，yfi），方位角φfi=atan2（fi，o），故Dubins曲线的终点状态为:qfi=［xfi，yfi，φfi］T。

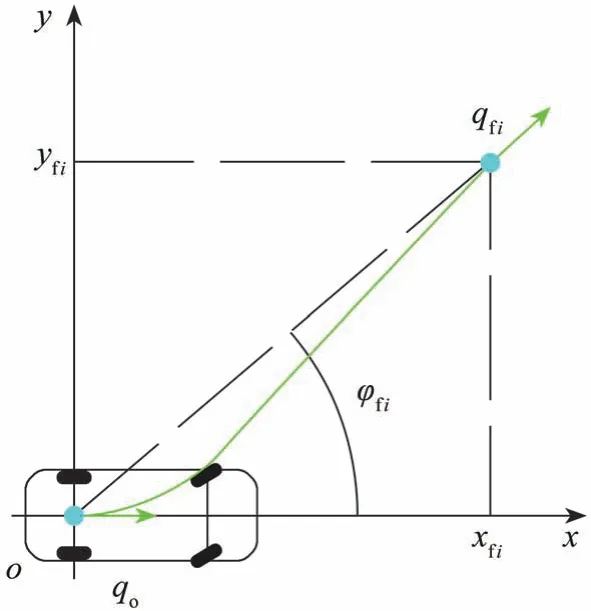
图6 生成Dubins曲线

当目标点进入传感器探测范围后，首先尝试满足目标点处的航向角要求。设目标点T在车辆坐标系下的状态为qt=［xt，yt，φt］T，那么首先尝试以qo为起点，qt为终点生成Dubins曲线，若成功，则以此为参考路径。否则，计算此时车辆坐标系下的目标点t的方位角φt′=atan2（t，o），并尝试以qt′=［xt，yt，φt′］T为终点生成Dubins曲线。

对于假设车辆可全向移动的Bug算法，在朝目标移动的状态时，一旦出现距离d（P，T）增大的情况，则认为存在局部最近点Mi，此时车辆的位置记作SWi，见图7。但对于存在最小转向半径的车辆，即使不受障碍物的影响，也会因为自身状态等原因远离目标点，如图8所示。此外，由于定位系统存在误差，即使车辆实际没有远离目标，也会出现距离d（P，T）增大的情况。而根据文献［13］可知:在TangentBug算法中，距离d（P，T）在朝目标移动状态下是非增的。因此，对于在某一时刻i的距离d′i（P，T），在朝目标移动状态时，除按目标点航向规划成功外，其取值由式（16）和式（17）确定，此时d′i（P，T）为当前时刻i之前到目标点距离的最小值。而其他情况下均为d′i（P，T）=di（P，T）。

图7 车辆轨迹示意图

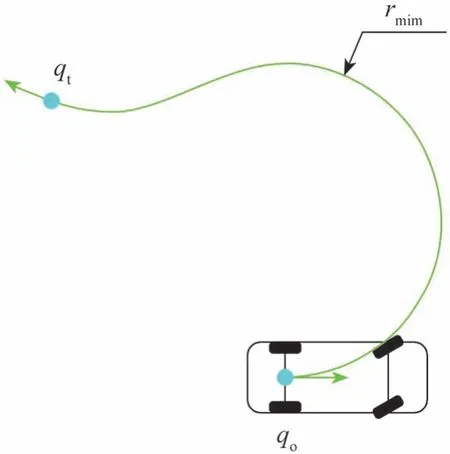
图8 车辆因最小转向半径而远离目标

设一距离阈值dm，若在某一时刻i，有式（18）成立，那么认为存在局部最近点Mi，随即切换为环绕障碍物状态。当在任何情况下均令d′i(P，T)=di（P，T），且dm=0时，对应定位系统无误差的理想情况。dm应结合定位系统的误差取一较小的正值。

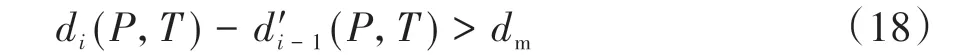
2.3.2 环绕障碍物状态

环绕障碍物状态算法的伪代码如表3所示。当处于环绕障碍物状态时，首先更新局部最近点Mi。设点Mi到目标点的距离为dmin，在初始化时令dmin=∞。若有式（19）成立，则更新dmin，并记录局部最近点Mi和车辆此时的位置SWi。

表3 环绕障碍物状态算法

设一集合L，有

若∃li∈L，使得从qo到qli=［xli，yli，atan2（li，o）］T生成的Dubins曲线通过碰撞检测，令dleave=d（li，t），那么有式（21）成立，即在集合F中存在一元素比局部最近点到目标点的距离更小，且生成的Dubins曲线通过碰撞检测。随后车辆切换为朝目标移动状态。记此时在惯性坐标系下的车辆坐标为点Li，li的坐标为LRi。在环绕障碍物状态下，dleave需要实时更新，在初始化时dleave=d（S，T）。

环绕障碍物的方向由状态转换时记录的目标方位确定，若此时atan2（t，o）＜0，则环绕方向为顺时针，否则为逆时针。以逆时针为例，如图7所示，车辆从状态转换点SWi处开始逆时针环绕障碍物，直到点Li处驶离障碍物。为防止在环绕障碍物状态下出现规划路径的局部振荡，以仅考虑自身前方信息的集合F′作为规划参考点集合。逆时针环绕时，按方位角由大到小的顺序对集合F′中的元素进行排序，而顺时针时，按由小到大的顺序排序。依次生成Dubins曲线并进行碰撞检测，一旦通过则以此作为参考路径，否则认为没有安全的路径并停车。

对于环绕障碍物一周的情况，由以下规则判断。

（1）若存在一车辆位置o，满足d（swi，o）＞dsw且|atan2（swi，o）|＞π/2，则认为车辆驶离状态转换点SWi，其中点swi为点SWi在车辆坐标系下的位置，dsw为距离阈值，可根据定位系统的误差取一较小的正值。

（2）在满足条件（1）的情况下，若存在一车辆位置o，满足d（swi，o）＜dsw且|atan2（swi，o）|＜π/2，则认为车辆再次回到点SWi。

当条件（1）和（2）均满足时，认为车辆绕障碍物一周回到了状态转换点SWi，即得出目标不可到达的结论并停车。

2.3.3 算法收敛性证明

车辆存在最小转向半径的运动约束不会影响本文算法的收敛性。如图8所示，若目标点位于测距传感器探测范围内，则车辆保持朝目标移动状态前进至目标点。若目标点位于测距传感器探测范围外，由于受最小转向半径的运动约束，车辆以朝目标移动状态远离目标，当满足式（18）后，切换为环绕障碍物状态。若在测距传感器探测范围内不存在障碍物，则距离dmin=∞；或虽然存在障碍物但未阻碍车辆运动，此时存在使规划路径通过碰撞检测的点LR，随后式（21）均成立。因此车辆的状态将在朝目标移动和环绕障碍物之间切换，直到车辆在朝目标移动的状态下不再满足式（18）。而在文献［13］中已经证明上述两种状态的组合不会导致TangentBug发散，故在有限次状态转换后车辆将保持在朝目标移动的状态到达目标点。

3 实车实验

3.1 实验平台搭建

为验证本文算法在真实环境中的表现，通过如图9所示的北京理工大学智能轮式车辆平台进行了实验。该平台为线控电动底盘，上位机可通过以太网转CAN设备（CANet）对底盘进行控制。传感器包括作为测距传感器的激光雷达和毫米波雷达，作为定位系统的惯性组合导航系统。软件算法在上位机中运行，程序指令通过CANet下发到CAN总线上，从而控制驱动电机和转向、制动执行器等设备，以实现车辆控制。

图9 实验车辆及关键零部件

实验的软件平台为Ubuntu 16.04和ROSKinet⁃ic，编程语言为C++。局部路径规划程序接收来自环境感知程序发布的障碍物信息和定位信息，并发布一条参考路径给运动控制程序。本文横向运动控制采用了预瞄控制算法，纵向运动控制采用了PID算法。本文局部路径规划算法主要参数的取值见表4。

表4 算法主要参数取值

3.2 实车实验验证

实验环境为工业园区，障碍物主要包括建筑物、花坛、货物和其他停放的车辆等。通过环境建模得到的规划参考点集合和局部栅格地图如图10所示，其中黑色的点为障碍物边界；蓝色的箭头为规划参考点集合，外围圆环为测距传感器探测边界上的点，其余为障碍物边界旋转采样后的点；红色的Dubins曲线为生成的参考路径。

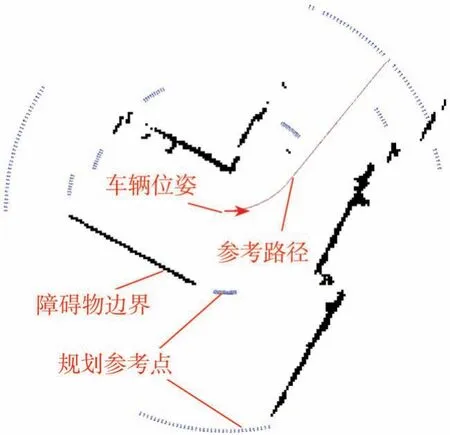
图10 实验场景下算法实时运行结果

实验测试场景有两种，场景1只包含朝目标移动的状态，场景2包含两种状态组合的情况，两种测试场景均通过了测试。场景1中车辆轨迹长度为113.248 m，场景2的轨迹长度为140.492 m。实验平台使用的上位机的配置为CPU i5⁃3450，8G内存。规划程序的控制周期固定在了0.05 s，每次循环实际计算时间如图11所示，其中场景1计算时间平均值为0.004 8 s，最大值为0.030 3 s，场景2计算时间平均值为0.006 6 s，最大值为0.030 1 s，由此可得该算法可满足实时运行的要求。

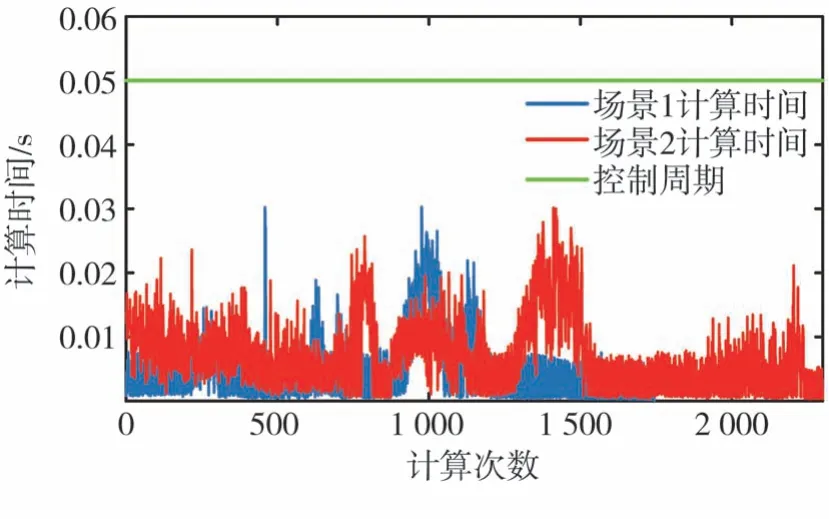
图11 每次循环算法实际计算时间

通过记录实验数据，离线运行LeGO⁃LOAM［18］分别得到场景1、2的全局地图和车辆轨迹如图12和图13所示。可以看出车辆在行驶的过程中避开了附近的障碍物，并在目标处按规定航向停止。在图12中，车辆以朝目标移动的状态避开了周围的障碍物，最终顺利到达目标点处。在图13中，车辆由于存在最小转向半径，从起点S开始远离目标点T，直到状态转换点SW1处，满足式（18）所述条件，记录下局部最近点M1后开始逆时针环绕障碍物。直到点L1处，由于存在点LR1比点M1离目标更近且生成的Dubins曲线通过了碰撞检测，故结束环绕障碍物的状态，并以朝目标移动的状态前进直到目标点处。

图12 场景1地图和车辆轨迹

图13 场景2地图和车辆轨迹

为验证本文算法对定位系统误差的鲁棒性，将式（17）改为:di′（P，T）=di（P，T），并令式（18）中的距离阈值dm=0，即不考虑定位系统的误差。重复场景1下的实验，得到的实验结果如图14所示。由于实际定位误差导致车辆与目标点间的距离增加，使得车辆由朝目标移动状态转换为环绕障碍物状态。由此可得，实际定位误差会对Bug类算法的稳定性产生影响，通过式（17）和对式（18）中距离阈值dm合理地取值，可避免因定位误差造成的状态转换问题，使得本文算法对定位误差的鲁棒性提高。

图14 定位系统误差对本文算法的影响

由于规划路径的曲率变化会直接影响运动控制程序的控制效果，故对本文算法生成的参考路径的平均曲率与文献［14］中用的圆弧作为参考路径的算法进行了对比分析。在场景1下两种算法生成的参考路径的平均曲率变化如图15所示，正值表示左转，负值表示右转。对两组数据进行分析，分别得到统计特征值如表5所示，对于参考路径平均曲率的标准差，融合圆弧曲线的算法为0.045 2，本文融合Dubins曲线的算法为0.025 3，提升了44%。对于参考路径平均曲率的最大值，融合圆弧曲线的算法为0.128 4，本文融合Dubins曲线的算法为0.068 0，提升了47%。由此可得，本文算法更有利于路径跟随控制。

图15 参考路径平均曲率对比

表5 参考路径平均曲率统计特征值

4 结论

本文中面向采用Ackermann转向的智能轮式车辆，针对仅能获取局部地图和定位信息的情况，提出了一种融合TangentBug和Dubins曲线的局部路径规划算法。首先通过采样的方法构建了规划参考点集合，无须构建局部切线图。然后以Dubins曲线作为规划路径，满足了车辆最小转向半径的运动约束和目标点处的航向要求，并通过加入沿规划路径的碰撞检测，提升了算法的安全性。结合TangentBug的证明结果，提出了适应定位系统误差的状态转换规则，并证明了车辆最小转向半径的运动约束不会影响本文算法的收敛性。最后通过实车实验证明了本文算法在真实环境下的可行性，结果表明:本文算法可规划出安全的局部参考路径，使车辆按规定位姿到达目标点，并可保证算法的实时性；本文提出的状态转换规则可有效避免定位误差的影响，提高了本文算法对定位误差的鲁棒性；相对于使用圆弧曲线，本文通过融合Dubins曲线规划出的路径更有利于路径跟随控制。