半透明胶条表面光条中心线提取

符钦伟，杜 宣，张 燕，吕 娜，陶 卫，赵 辉*

（1.上海交通大学 仪器科学与工程系，上海200240；2.上海航天技术研究院，上海201109）

1 引言

在工业生产中，自动点胶机已经广泛应用于电子零部件、印刷电路板、半导体封装等领域的黏接环节。为了防止涂覆的半透明胶条过多导致溢胶，或者过少导致松动，对其截面轮廓进行在线测量和质量评估是必不可少的环节。作为一种典型的半透明物体，胶条因其黏合特性，无法使用接触式测量方法。线结构光三角测量是一种无损检测方法，以其测量精度高、速度快、结构简单等优势［1］，可以应用于半透明胶条的实时轮廓测量。

被测物体的线轮廓是指位于物体外表面的通过面与面相交的方式构成的直线或曲线［2］。而在基于激光三角法的线结构光轮廓测量系统中，所采集图像中包含物体线轮廓信息的激光条纹具有一定宽度，为了准确测量被测物体的轮廓，必须要精确提取激光条纹的亚像素线条［3］。对于不透明表面的物体，激光条纹的理想位置近似于条纹能量中心，直接采用传统中心线提取方法就能够准确提取光条中心。目前，常见的激光条纹中心线提取算法有灰度重心法、极值法、高斯拟合法和Steger算法等。灰度重心法是利用灰度作为权重来求条纹的能量中心，适用于信噪比高且比较细的激光条纹；极值法对于出现多个极大值点的情况误差较大；高斯拟合法则是利用条纹的灰度值序列拟合成高斯曲线并把极值点作为中心位置，其缺点是不适用于半透明物体激光条纹的非高斯分布灰度值序列。Steger算法利用Hessian矩阵计算条纹法线方向，将该方向上的极值点作为中心位置，其缺点是算法时间复杂度高，无法用于在线测量［4］。贾倩倩等人利用灰度的梯度方向代替光条曲线的法线方向，减少了计算耗时［5］。田庆国等人利用轮廓多边形表示实时提取光带中心线，并设计了自适应横截面宽度变化的灰度重心法计算亚像素中心坐标［6］。刘振等人以互相关极大值对应的条纹作为初始光条纹中心，并通过曲线拟合法定位条纹中心，能够降低噪声的干扰［7］。杨毅等人通过预处理和灰度重心法先提取条纹中心线的初始值，先用均值法一次平滑初始值，然后采用Savitzky-Golay滤波算法二次平滑，提高了灰度重心法的速度以及精度［8］。蔡怀宇等人用主成分分析（PCA）法代替Steger算法中利用Hessian矩阵求条纹法线的过程，提高了测量速度［9］。刘剑等人通过Hessian矩阵和区域增长相结合的方法提取激光条纹中心线，降低均方差的同时，提取速度相比于Steger算法提高了40倍［10］。但是对于半透明胶条而言，激光条纹成像受到次表面散射的干扰，灰度值序列并非高斯分布，理想位置也并非能量中心位置。若采用上述中心线提取算法提取半透明物体的激光条纹理想中心位置，提取精度会大幅下降，提取结果也会出现错误。本文提出一种基于线结构光的半透明胶条表面光条中心线提取算法，通过分析激光条纹成像机理和灰度分布特征，得出灰度序列中直接反射分量区别于次表面散射分量的特征，再从灰度序列中分离出直接反射分量，最后采用灰度重心法处理直接反射分量得到亚像素中心位置坐标。

2 激光条纹图像的灰度分布特征分析

2.1 激光条纹成像机理

相比于不透明物体，半透明胶条具有一定的透射率，而不同材料的表面透射率会导致激光条纹成像的差异。如图1所示，不透明胶条的激光条纹图像信噪比高，条纹较细，光条中心线容易提取；而半透明胶条的激光条纹图像信噪比低，条纹较粗，光条中心线提取难度大。

图1 不同胶条的激光条纹图像Fig.1 Laser stripe images of different glue strips

相比于不透明胶条，半透明胶条会发生次表面散射现象，这是造成激光条纹成像质量严重下降的主要原因。如图2所示，对于不透明胶条，线结构光束在物体表面发生漫反射，光线朝不同方向反射，在一定反射方向范围内的光线入射到镜头中，光线最终聚焦在光电传感器平面上成像。线结构光只照射在物体表面的一个截面上，理想的激光条纹成像应该只包含该截面上的轮廓信息。而对于半透明胶条，线结构光照射在半透明胶条表面，一部分光线在胶条表面直接反射进入镜头聚焦成像；另一部分光线垂直透射进入半透明胶条的内部，与一些不规则形状的微粒发生碰撞，经过单次散射或者多次散射从非入射点的其他截面出射，并经过镜头聚焦到光电传感器平面上成像。因此，相机采集到的光线包括直接反射分量和次表面散射分量两部分，即激光条纹不仅包括线结构光入射截面上的物体表面轮廓特征，还包括次表面散射而产生的其他非入射截面的轮廓特征，从而导致半透明物体激光条纹图像的信噪比降低。

图2 激光条纹成像原理Fig.2 Principle for laser stripe imaging

2.2 灰度分布特征分析

光条中心线提取通常是将激光条纹图像的每一列或行（取决于激光条纹方向）作为独立信号来分析［11］。为了准确提取光条中心线，需要在灰度序列中分离直接反射分量与次表面散射分量，明确光条中心在条纹中的分布位置。

对于理想的不透明目标漫反射表面，线结构光在单个截面上的灰度值呈高斯分布，如图3所示。此时，理论上的中心位置坐标就对应于灰度值最大点的坐标［12］。

图3 理想激光条纹的灰度值分布Fig.3 Gray value distribution of ideal laser stripe

对于实际的不透明胶条，其激光条纹图像的截面灰度类似高斯分布，如图4（a）所示，集中为单峰，两侧灰度值较小且近似对称分布。对于此类激光条纹，采用灰度重心法能够准确提取中心位置。但是对于半透明胶条，激光条纹图像截面的灰度值分布出现了很大的差异。如图4（b）所示，可以看出截面灰度序列不再为高斯分布，最高峰灰度值较小，且在最高峰的两侧灰度也不是对称分布。

图4 激光条纹的一维灰度值分布Fig.4 One-dimensional gray value distribution of laser stripes

为了从灰度值序列中分离出直接反射分量，本文对半透明胶条的表面直接反射和次表面散射分布进行了建模分析。如图5所示，在直射式激光三角测量系统中，线激光器发射出一定宽度并且呈高斯分布的光束，垂直照射在半透明胶条的表面，镜头和相机组成的成像模组倾斜一定角度拍摄激光条纹图像。假设原始激光束功率为l，相机视场角为α，半透明胶条的透射率为λ，表面法线和激光方向的夹角为β，忽略光束在空气中传播的能量损耗。那么，对于反射截面上所有角度的光，只有在相机视场角范围内才能成像，在表面发生直接反射后入射在成像平面上的光线功率为l1，则有：

直接反射分量与高斯分布的激光束直接相关，在灰度序列上表现为独立的波峰。若激光方向垂直于物体表面，即β=0，公式（1）可以表示为：

其余的光线垂直透射进入胶条内部，遇到微粒发生次表面散射，分为单次散射和多次散射。单次散射是指光线在物体内部和微粒发生一次碰撞后出射，多次散射则是指光线在物体内部和微粒发生了两次及以上的碰撞后出射。其中，发生单次散射的光线直接从胶条表面出射。由于半透明胶条介质的折射率大于空气，非相机一侧（图5左侧）的单次散射分量不可能入射到相机的成像平面上，只有部分偏相机一侧（图5右侧）的单次散射分量最终入射到相机成像平面上。在单次散射模型中，出射光线的功率与入射光线的功率、介质吸收系数σt、散射系数σs、单次散射传播距离d，以及表示散射分布的不对称性的相位函数p(θ)有关，其中θ是指单次散射光线与入射光线的夹角［13-14］。因此，入射到成像平面上的单次散射分量功率l2为：

相对于表面直接反射分量，入射到成像平面上的单次散射分量偏向相机一侧（图5右侧）移动。单次散射分量也与高斯分布的激光束直接相关，在灰度序列上表现为独立的波峰，且与直接反射分量的波峰位置不同。在图4（b）所示的灰度序列中，即直接反射分量波峰的横坐标（行像素坐标值）小于单次散射分量波峰。另外，多次散射分量在胶条内部经过多次碰撞反射后从胶条表面出射，左右两侧都存在多次散射分量，相互叠加后的部分多次散射分量入射到成像表面。根据式（3）可知，多次散射随着散射次数的增加呈指数衰减，因此相比于直接反射分量和单次散射分量，最终入射到成像表面的多次散射分量功率最小。而且多次散射分量从胶条表面一个范围内均匀出射，因此在灰度序列中表现为一个范围内灰度值的增加，没有形成独立的波峰。

图5 半透明胶条的光线反射和散射分布Fig.5 Light reflection and scattering distribution on trans⁃lucent glue strip

3 光条中心线提取算法

上述分析表明，半透明胶条激光条纹的每一列都可以作为独立的一维灰度信号来分析。由于激光光束本身具有一定宽度且呈高斯分布，直接反射分量和单次散射分量均形成一定宽度的独立波峰且位置不同，波峰灰度值的相对大小则与半透明胶条的材料参数有关。因此，本文首先通过数学形态学方法提取出一维灰度信号中满足一定宽度的波峰特征，然后根据波峰灰度值的相对大小及位置提取直接分量波峰，最后在直接分量波峰位置开窗利用灰度重心法提取中心位置坐标。具体算法流程如图6所示。

图6 一维灰度值信号中心位置坐标提取算法流程Fig.6 Algorithm flow chart of center position coordinates extraction for one-dimensional gray value signal

数学形态学中的基本运算包括腐蚀和膨胀两种操作。在一维信号处理中，设一维信号序列f(n)，n=0，1，...，N-1，其 中 的 结 构 元 素 可 以用k(m)，m=0，1，...，M-1表 示，且N＞M。那么结构元素k(m)对信号f(n)的腐蚀定义为：

其中i=0，1，…，N-M。

结构元素k(m)对信号f(n)的膨胀定义为：

其中i=M-1，M，…，N-1。

这两种基本运算又可以组合为开运算和闭运算，开运算是指对信号先进行腐蚀运算然后进行膨胀运算：

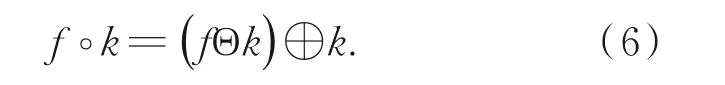
闭运算则指对信号先进行膨胀运算然后进行腐蚀运算：

开运算可以削掉波峰，从底部平滑信号；而闭运算则可以用于填充波谷，提取信号的波峰包络线［15］。为了不破坏波峰的几何特征，需要选择合适长度的零振幅水平结构元素。通过如下的处理流程，可以得到感兴趣的波峰特征：（1）通过闭运算滤除像素宽度较小的突变波峰，得到包含感兴趣波峰特征的包络线；（2）然后对包络线进行开运算得到波峰的基线；（3）用闭运算提取的包络线和开运算提取的波峰基线做差，即可提取到感兴趣的波峰特征。提取过程如图7所示，根据激光线宽及本测量系统的设置，结构元素与激光成像宽度一致，最终选择长度为21的零振幅结构元素，提取有效波峰特征。

图7 波峰特征提取过程Fig.7 Extraction process of peak characteristics

波峰包络线和基线差分提取到的多个波峰特征中，不仅包含了直接反射分量波峰，还包含了部分次表面散射分量波峰，根据波峰灰度值进一步确定中心位置。根据2.2中的分析，次表面散射分量的波峰分布在与激光束入射点不重合的位置，只有直接反射分量代表的是入射点位置的轮廓信息。零振幅结构元素的开闭运算没有改变波峰所在的位置，通过差分结果确定了波峰所在的行坐标，原始信号中已知波峰对应的灰度值。直接反射分量的波峰灰度值跟线激光功率、半透明材料透射率和表面粗糙度等有关，而且它与次表面散射分量波峰灰度值的相对大小跟半透明材料本身有关，不同材料差异很大［16］。由于多次散射的功率最小，直接反射分量波峰和单次散射分量是灰度值最高的两个波峰，两者的相对大小不确定，但是根据相对位置可以判断出直接反射分量波峰。因此，针对上一步采用数学形态学方法提取出来的多个特征峰，选取出波峰灰度值最大的两个波峰，其中行坐标较小的波峰代表直接反射分量，其坐标值作为直接反射分量的所在位置x。

根据零振幅结构元素的长度M，在原始一维灰度值信号的波峰处开窗[x-M/2，x+M/2]。针对该窗范围内的一维灰度值序列采用灰度重心方法提取到亚像素坐标值，作为该列条纹的中心位置。图8给出了中心位置提取过程，逐列扫描处理一维灰度值信号，最终得到整个半透明胶条激光条纹的中心线。

图8 中心位置坐标提取过程Fig.8 Extraction process of center position coordinates

4 实验

4.1 实验装置

本实验采用的线结构光直射式轮廓测量系统如图9所示。其中，线激光器的管芯功率为30 mW，激光波长为405 nm，工作距离100 mm处的最小线宽为0.1 mm；物方远心镜头选用大恒图像的GCO-260611，工作距离为65 mm，景深为2.99 mm；数字相机选用水星相机MER-310-12UC，靶面尺寸为1.27 cm（1/2 inch），分辨率为2048×1536。被测物体为半透明胶条，其高度约为1～2 mm，宽度约为3～4 mm。

图9 线结构光直射式轮廓测量示意图Fig.9 Schematic diagram of line-structured light direct incident contour measurement

4.2 实验结果及分析

使用夹具将半透明胶条所涂覆的手机背板固定于光学平台上，保证其稳定性。

通过对比半透明胶条同一截面灰化前后的激光条纹图像，验证了2.2中对直接反射分量和次表面散射分量在灰度序列上相对位置分布的分析。图10（a）是灰化后的激光条纹，图10（b）是半透明胶条的激光条纹，图10（c）中获得灰化后胶条表面光条中心线，图10（d）将理想光条中心线叠加在半透明胶条激光条纹上，验证了在该激光条纹图像中次表面散射分量的主要组成部分即单次散射分量分布于直接散射分量的下侧。

图10 半透明胶条激光条纹及理想光条中心线Fig.10 Laser stripe images and ideal laser stripe center line of translucent glue strip

针对同一截面条纹图像，分别采用灰度重心法和本文方法提取半透明胶条表面光条中心线，提取结果如图11所示。针对该截面灰化后的激光条纹图像，采用灰度重心法获得光条中心线，由于半透明胶条的表面轮廓近似二次曲线，采用二次曲线拟合获得理想的光条中心线。该条纹图像属于典型的半透明胶条激光条纹图像，条纹粗大，直接反射分量特征不明显，提取难度大。灰度重心法求得的光条中心线偏条纹下侧，与理想光条中心线偏差大，提取结果出现错误。本文方法较为准确地提取得到半透明胶条表面光条中心线，偏差较小，更接近理想光条中心线，并且经过二次曲线拟合后中心线更加平滑。

图11 不同光条中心线提取方法对比Fig.11 Comparison of different laser stripe center line ex⁃traction methods

将不同方法提取到的光条中心线数据与理想的光条中心线数据做差并求平均，得到各个方法的平均误差，并以此作为评判提取方法好坏的量化判据。从表1可以看出，灰度重心法的平均误差约为35.72 pixels，本文方法有效降低了提取平均误差，达到3.197 pixels，说明本文方法基本去除了次表面散射干扰。在本文方法的基础上进行二次曲线拟合，平均误差达到0.714 pixels。误差量化分析表明，灰度重心法等传统中心线提取方法不适用于提取受到次表面散射干扰的半透明激光条纹光条中心线，本文从灰度序列中提取出直接反射分量并求得亚像素中心位置坐标，经过拟合后平均误差能达到亚像素级别。

表1 不同光条中心线提取方法的平均误差Tab.1 Average errors of different laser stripe center line extraction methods （pixel）

实验还采集了一种其他形状和材质的半透明胶条，灰化前后其激光条纹如图12所示，提取光条中心线的平均误差达到3.708 pixel，由此验证了本文方法的普适性。

图12 其他形状半透明胶条的激光条纹Fig.12 Laser stripes of translucent strip in other shape

5 结论

针对半透明胶条次表面散射导致的图像信噪比显著下降且灰度分布严重变化等问题，本文分析了灰度序列中直接反射分量和次表面散射分量的波峰大小及位置分布，并提出一种半透明胶条表面光条中心线提取算法。首先选择一定宽度的零振幅水平结构元素，使用闭运算获得一维灰度信号中有效波峰的包络线，再通过开运算获得波峰包络线的基线；然后通过差分运算，获得包含了直接反射波峰的多个波峰特征，确定波峰所在行坐标；最后根据波峰灰度值及位置分布，提取得到直接反射分量波峰，在其坐标位置开窗使用灰度重心法进一步获得亚像素中心位置坐标，扫描处理获得半透明胶条的表面亚像素光条中心线。针对同一条纹图像，传统的无预处理的灰度重心法提取的中心线结果误差很大，本文方法提取结果的平均误差较小，为3.197 pixel，二次曲线拟合平均误差为0.714 pixel。本文方法有效排除了次表面散射分量的干扰，能够准确提取半透明胶条表面光条中心线。