基于最小二乘配置的地面三维脉冲激光扫描仪自检校

郭献涛，贾 燕

（南京邮电大学 地理与生物信息学院，江苏 南京210023）

1 引言

地面激光扫描（Terrestrial Laser Scanning，TLS）技术又称实景复制技术，它是测绘领域中继GPS之后的又一次技术革命。该技术通过极坐标法扫描测量激光到对象表面的距离、水平角及垂直角，可以快速、高精度、免棱镜式地获取对象表面的高密度三维数据，得到对象的离散化表示；但TLS测量精度较大程度上受仪器系统误差影响，为保证数据质量，须在实际扫描测量前对仪器实施检校［1］。

目前，关于TLS仪器的检校还没有通用的方法与评价体系，主要有分项检校和整体检校两种模式。分项检校主要采用误差分析法对测距测角等模块实施单独检校，需精确建立仪器的误差模型，受扫描仪专利设计影响，这方面的知识通常较为有限［2］。此外，该类检校还需检校基线等特殊检校设施，因此难以普及。整体检校是将扫描仪所有组件作为一个整体，直接与标准检校场比较测量来获取系统改正数。该类检校无需精确已知仪器的误差模型，检校场建立也不复杂，目前可通过自检校实施整体检校［3］。

近年来，自检校已逐渐成为TLS检校的流行方法，它可以确定扫描仪所有系统误差及其他系统参数。基于使用的检校标志类型，TLS自检校可分为两种类型［4］：（1）基于点的自检校，即利用可提取中心坐标的标志实施检校。Lichti给出了一个自由网平差法，以同时估计外方位参数、对象点坐标与检校参数［5］，检校了Faro 880、Trim⁃ble GS200、Trimble GX等扫描仪，并分析了检校参数的时序行为，文献［6］详细描述了上述数学模型。Krzysztof对扫描仪FARO 880实施了一系列自检校实验，较好地识别了TLS仪器误差［7］。此外，Soudarissanane等人给出了一个全景相机扩展传感器模型作为TLS误差模型，使用扫描强度图像代替点云对激光扫描仪Imager 5003实施建模和检校［8］。目前这些研究主要集中于相位式扫描仪，且检校参数间存在高相关性导致参数估计不确定性的问题。（2）基于平面的自检校，即利用平面模板反射坐标实施检校，该方法由Gielsdorf提出，并被应用于扫描仪Imager 5003与PoMeS的实验室检校［9］。Chow改进了该方法，利用室内墙壁、地板和天花板代替专门的检校面板实施了扫描仪FARO880的自检校，改善了自检校残差标准差的观测精度。Dorninger等人使用平面特征进行自校准，主要专注于现场闭合差估计［10］。此外，Mahbaz建议采用连续分段线性改正函数替代谐波函数和多项式函数［11］，该改正函数不需要对检校模型做假设，但需要更多的参数。相比于点检校法，基于平面的自检校法无需做大量的单点测量，但结果却与基于点自检校方法相差较大，使系统的误差识别复杂化。

本文基于点自检校法提出一种脉冲TLS扫描仪检校方法，以降低参数估计的相关性，保证参数估计的可靠性。

2 建模与优化设计

2.1 自检校建模

TLS检校的首要步骤是解决扫描仪几何建模的问题。由于扫描仪的专利设计，用户通常难以了解其内部构造，需要对仪器模型做一定的假设［12］。TLS在测量原理（见图1）上类似于免棱镜测量的全站仪［13］，本文拟采用全站仪的误差模型作为自检校的基础模型。

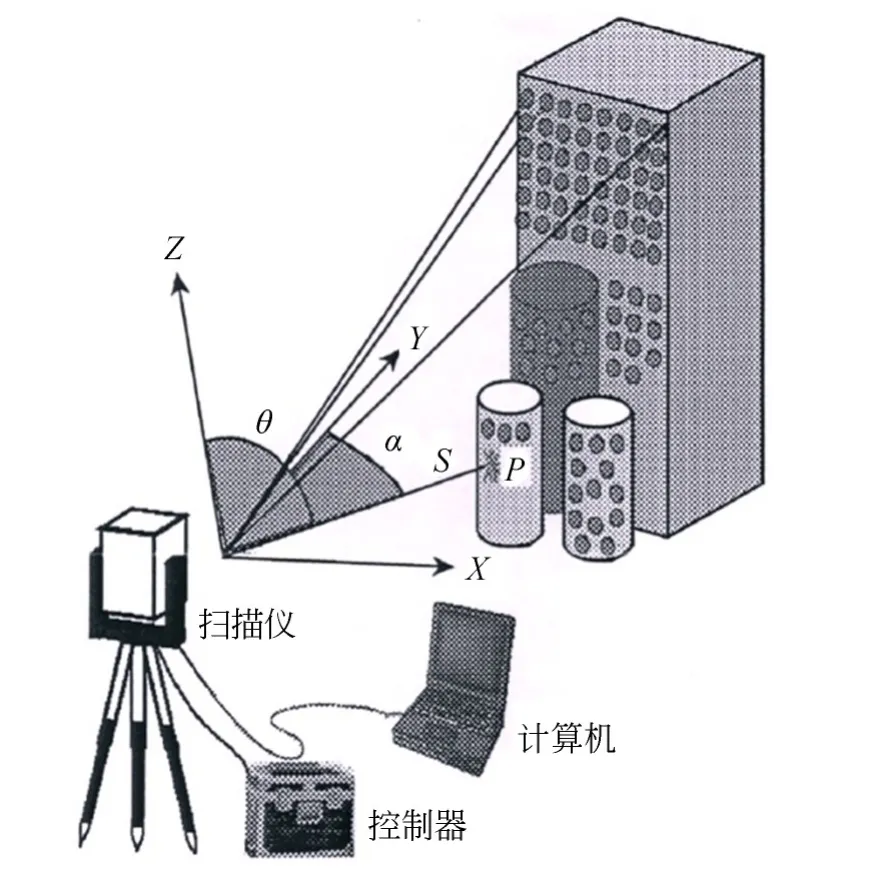
图1 地面三维脉冲激光扫描测量的基本原理Fig.1 Basic principle for terrestrial laser scanning

参考全站仪的误差模型，拟定该模型的主要检校参数（Calibration Parameters，CPs）为激光测距仪的零误差（加常数）、水平轴误差、视准轴误差、竖盘指标差以及尺度误差。采用这些参数实施检校后，残差中可能还会残留一些系统趋势。对这些趋势进行分析以确定其他的CPs。

2.2 检校网优化设计

TLS检校网的最优设计应能保持与其他系统参数较低相关性的前提下，提供CPs的可靠估计［14］，主要分为零类设计和一类设计两部分。

2.2.1 零类设计

检校网零类设计又称检校网基准设计，可基于最小化约束或内部约束定义TLS检校网基准。常见的内部约束是通过对象点坐标（Object Point coordinates，OPs）实施基准约束，其约束参数精度较好，但会导致一些系统参数间（主要是外 方 位 参 数（Exterior Orientation Parameters，EOPs）与CPs间的高相关性。

最小化约束通常是固定TLS测站的方位和位置，或固定非共线的3个对象点的坐标，但该约束易增加一些CPs和OPs间的相关性［15］。所以，以上约束都不是TLS检校网基准设计的最佳选择。本文摒弃此类强制约束，采用最小二乘配置先验随机信息柔性定义检校网基准。

2.2.2 一类设计

检校网一类设计，即检校网结构图形设计。基于前人实施相机检校以及TLS检校的成果与经验，为得到CPs的低相关高精度估计，本文拟采用以下检校网配置：

（1）使用两个或两个以上扫描仪位置估计测距仪加常数；（2）使用大量的点状标志提供平差观测的高冗余度，确保有效检测非模型系统误差导致的残差趋势；（3）检校标志在垂直方向均匀分布，保证垂直角依赖误差（如水平轴误差、视准轴误差）的可靠估计；（4）从同一标称位置实施正交扫描，以降低EOPs和CPs间的相关性。

3 方 法

传统利用参数化模型或混合最小二乘平差模型实施TLS自检校，通常把一部分变量视为观测值，其他视为参数。伴随观测值的是以标准差或方差-协方差（Variance-Covariance，VCV）矩阵形式存在的先验随机信息，而对于参数并没有给出这些信息。

本文提出的方法通过最小二乘配置对检校平差中的所有参数配置先验权重，把模型中的全部变量作为观测值。对TLS自检校来说，其主要优势是易于引入EOPs先验随机信息。同时，通过“随机约束”定义检校网基准，从而避免了强制约束易导致参数间高相关性的不足。

3.1 检校模型

本文方法的底层数学模型是附有检校参数与外方位信息的扫描仪坐标系统与外部坐标系统之间的刚性变换。假设在检校场中利用点状检校标志进行检校，且每站实施一次扫描，则从第i站扫描测量第j个检校标志的条件方程为：

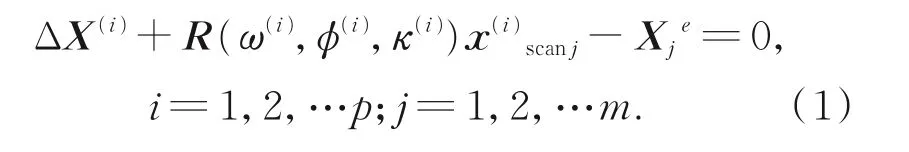
式中：p为扫描仪测站数，m为检校标志数，ΔX(i)表示第i个扫描站的平移向量，R(ω(i)，ϕ(i)，κ(i))表示坐标系统间的旋转矩阵，X je为第j个检校标志的外部坐标向量，x(i)scanj为在第i站上扫描第j个检校标志校正扫描仪CPs影响后的扫描仪坐标向量，ΔX，ΔY，ΔZ，ω，φ，κ为扫描仪外方位参数。其中：

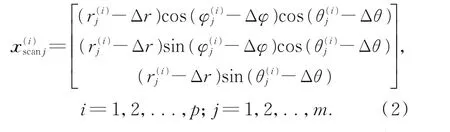
式中r，φ，θ分别为斜距、水平角与垂直角。误差项 Δr，Δφ，Δθ的 建 模 为 ：Δr=a0，Δφ=b1/cosθj(i)+b2tanθj(i)，Δθ=c0，而a0，b1，b2和c0分别表示测距仪加常数、视准轴误差、水平轴误差与竖盘指标差。由于检校场尺寸通常较为有限，尺度参数估计较弱，本文检校模型中没有包含该误差参数。

由于参数和观测隐性相关，选择线性化混合平差模型。式（1）线性化可得：

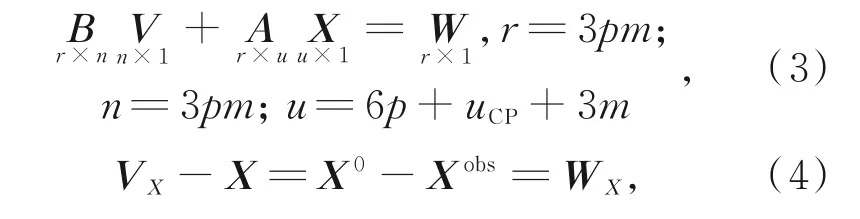
式中：A，B分别为式（1）关于参数和扫描观测的衍生矩阵，W与W X为闭合差向量，X为参数向量，其近似值为X0；Xobs，V X分别为参数“观测”值与“观测”参数有关的残差向量，uCP为CPs数量。式（3）和式（4）联立得到：

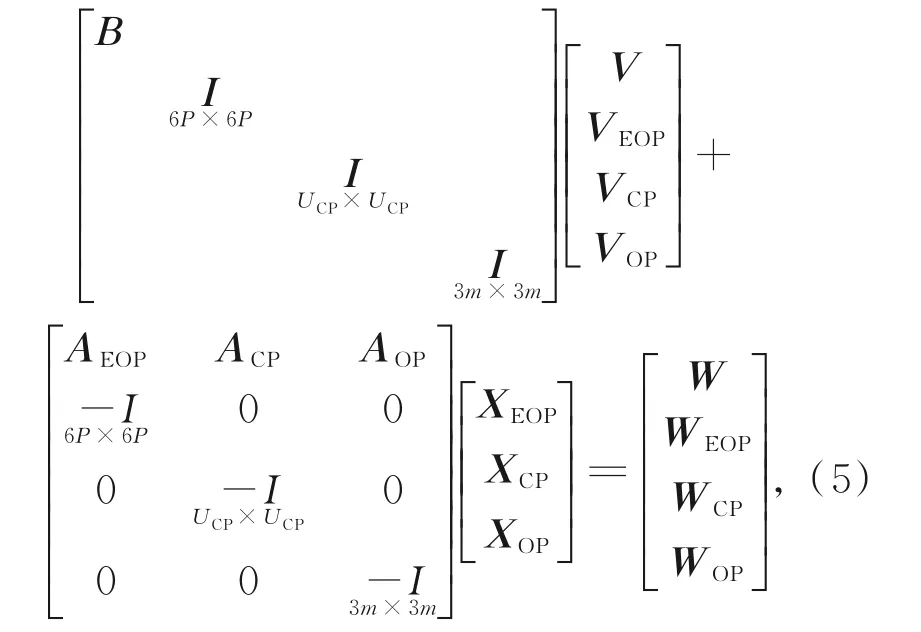
式中：向量X，W X，V X及矩阵A被分解为三部分，分别对应扫描站EOPs(AEOP，XEOP，WEOP，VEOP)、扫 描 仪 CPs(ACP，XCP，WCP，VCP)与 OPs（AOP，XOP，WOP，VOP）。

其平差先验VCV矩阵计算如下：

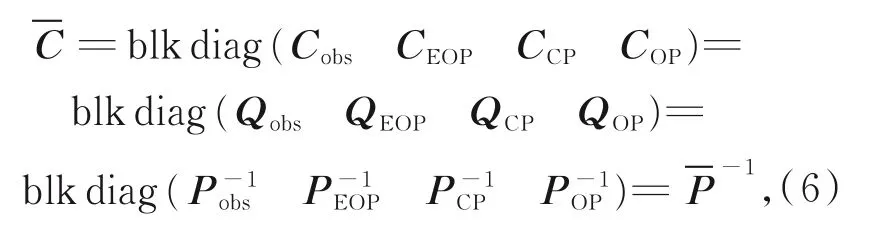
式中：C为VCV矩阵，Q为辅因子矩阵，P为权重矩阵。在平差开始，假设先验方差因子σ20=1.0，并假设式（6）中系统参数各不相关。VCV的子矩阵Cobs为：

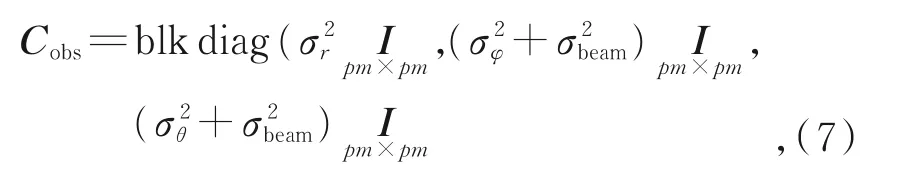
式中：σr，σφ，σθ分别表示测距、水平方向与垂直角的先验信息（标准差），参考仪器说明书设定；σbeam表示激光光斑内测距位置的不确定性，约等于波束宽度的1/4。

X的法方程系统表示为：

式中：

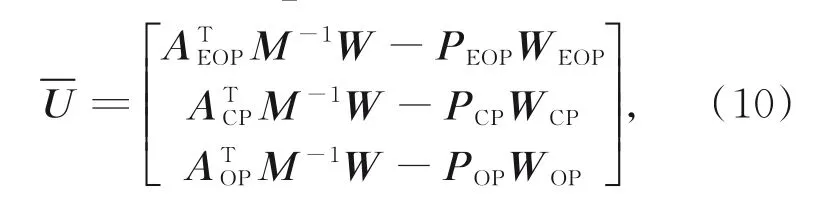
式中：

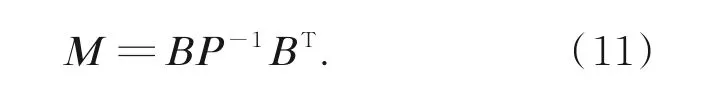
则解变为：

为消除设计矩阵基准秩亏及应对传统约束导致的高相关性，代替引入OPs作为观测值，对其坐标引入内部约束。该模型中随机内部约束为：

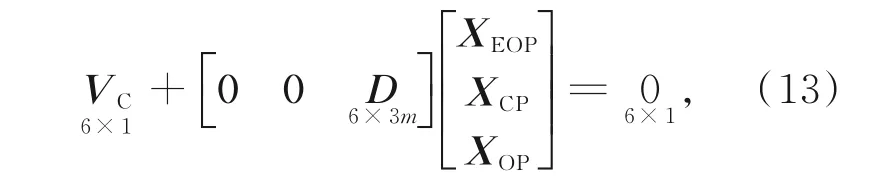
式中：VC是约束下的残差向量，D为内部约束矩阵。本文估计的不是OPs，而是其近似值的改正（XOP）。将式（5）转变为下列矩阵方程：

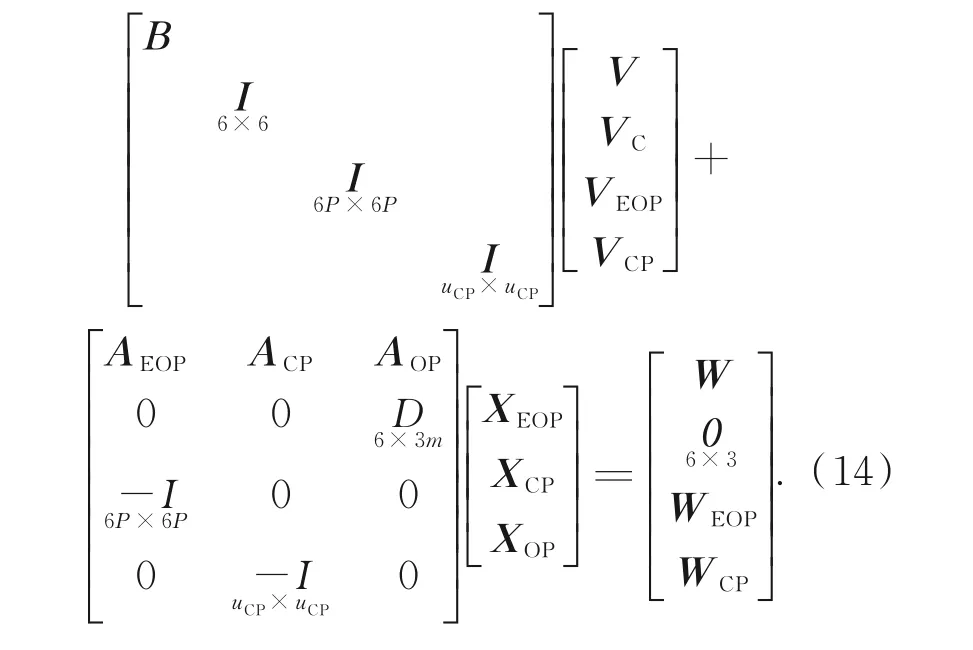
其约束平差的先验VCV矩阵为：

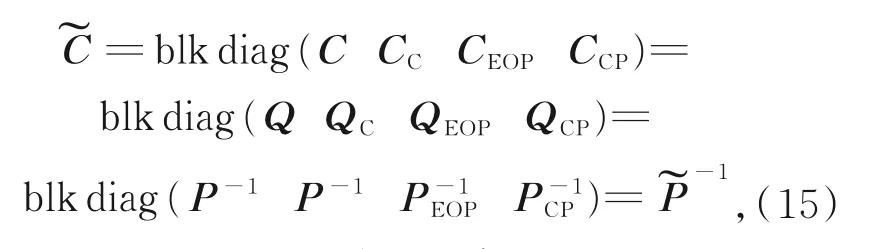
式中：CC，QC和PC分别为约束下“观测”的VCV矩阵、辅因子矩阵与权重矩阵。具体实施中，矩阵CC和QC可设置为单位矩阵乘以一个极小数，矩阵PC中对角元素趋向无穷大。同式（12）求解内部约束的平差解。

3.2 方差分量估计与粗差检测

在TLS自检校过程中需要利用后验方差分量估计观测精度，以评估检校平差中使用的先验观测权重是否合理。此外，为了成功实施后验方差分量估计须剔除粗差，而要有效检验粗差，观测VCV矩阵应正确无误，因此，需同时实施方差分量估计和粗差检验。

本文采用Forstner法同时实施方差分量估计和鲁棒估计［16］。首先利用检校模型中计算的方差-协方差矩阵实施最小二乘平差，然后通过以下权重基于平差残差计算新的等价权矩阵，即有：

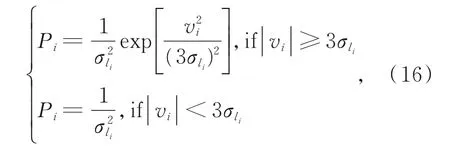
式中σl i和v i分别为第i站观测的先验标准差和残差。根据以上加权法则，具有较大残差的观测被视为异常值，使用残差指数函数降低其权重，持续迭代直至收敛。

最后，估计观测方差分量，并利用F测试检验它是否与先验值存在显著差异，若不显著，则接受平差结果；若显著，则计算新的后验权矩阵，并重复上述检校流程。

4 实验

为了测试本文方法的性能以及找到CPs之间以及CPs和其他系统参数间低相关性的最优检校网设计，利用扫描仪Leica Scan Station（具有直接地理定位功能）在一个12 m×9 m×3 m的室内检校场中实施自检校实验（见图2）。

图2 检校场设计平面图Fig.2 Schematic diagram of self-calibration field

该实验场包含144个均匀分布于检校场空间（墙壁、地板和天花板上）的点状检校标志，其垂直分布范围为-45°～83°，几乎覆盖了整个垂直维扫描视场，分别采用2站和4站扫描设置实施两个系列的模拟自检校实验（具体设计见表1）。

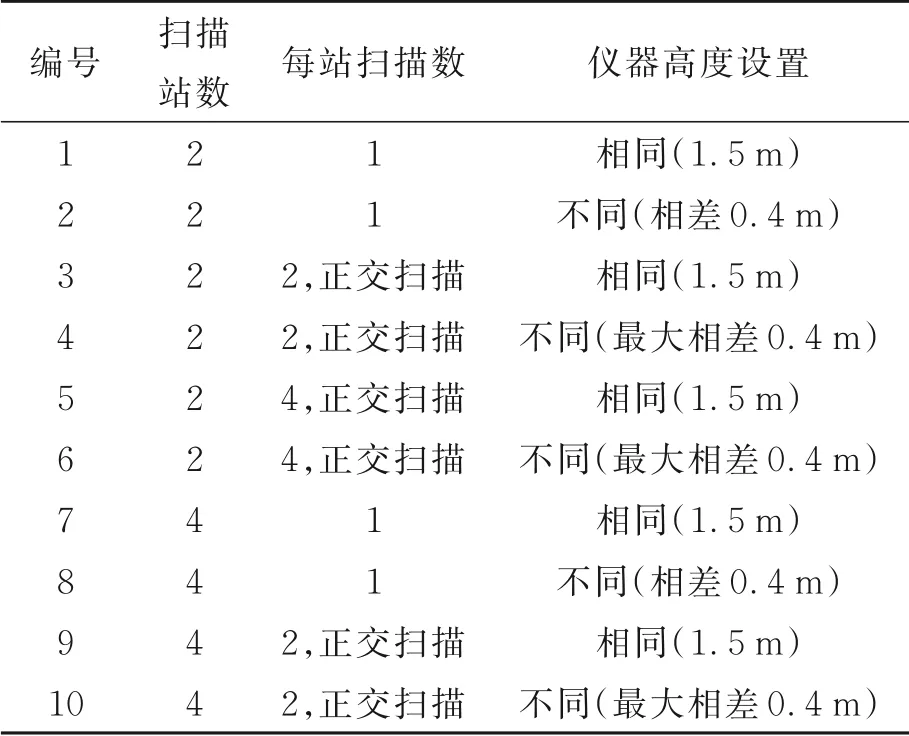
表1 自检校模拟设计Tab.1 Specific indexes of self-calibration test

实验中采用的扫描仪观测先验标准差从仪器说明书中获取，误差项σbeams忽略不计，扫描仪CPs先验标准差参考前人研究成果设置（见表2）；OPs先验标准差基于假设“其中一站扫描的检校标志坐标可作为OPs的先验值”；EOPs先验标准差参考扫描仪可实现的对中整平精度；扫描方位先验精度可设为一较大值，以实现该参数的完全自由。最后，加入随机噪声（对应于各个观测的标准差）到扫描仪观测、扫描仪中心坐标和“倾”角中。

表2 自检校中模拟CPsTab.2 Simulation of CPs in self-calibration test

根据表1中的实验设计，分别实施两个系列的检校实验。在第一个系列实验中不加入任何已知点，在第二个实验系列中加入3个位置分布良好的已知检校标志（XYZ坐标先验标准差约为1 mm），以研究已知点对模拟结果的影响。

5 结果与分析

5.1 实验结果

检校实验结果见表3与表4（篇幅所限，仅给出部分扫描站检校数据）以及图3和图4（图中无已知点参与的结果以黑色表示，包含3个已知点的模拟结果以灰色表示）。表3和表4中给出了估计的CPs以及其标准差信息、EOPs和OPs的相关系数（最大绝对值）以及平均标准偏差信息。由于扫描仪自检校中主要关注CPs的精确估计，所以表中仅给出了CPs和其他系统参数间的相关系数。这里用ρ表示相关系数。

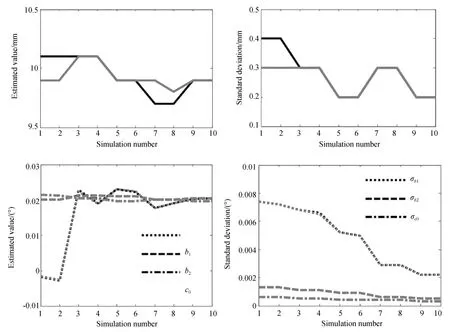
图3 自检校模拟得到的CPs估计和标准差Fig.3 Estimation and standard deviations of CPs in self-calibration simulation

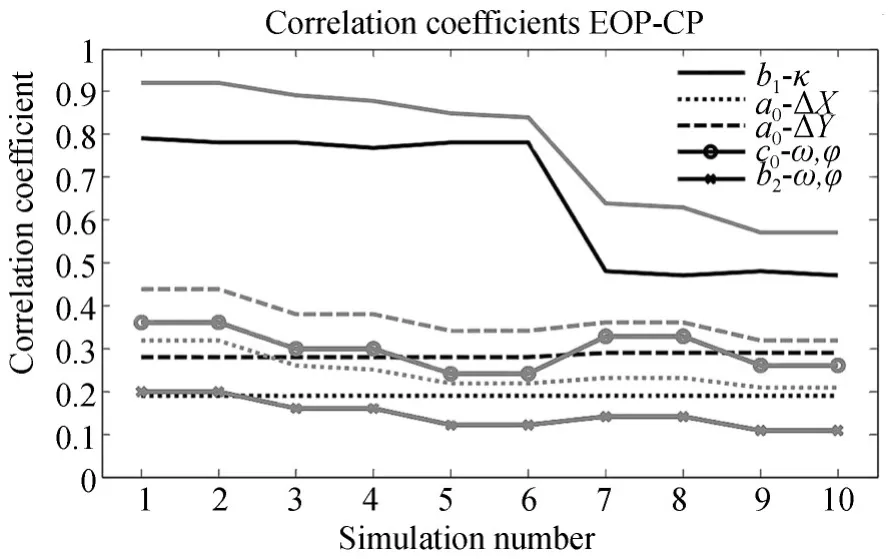
图4 自检校模拟中不同参数间最大（绝对值）相关系数Fig.4 Maximal correlation coefficients（absolute value）between different parameters

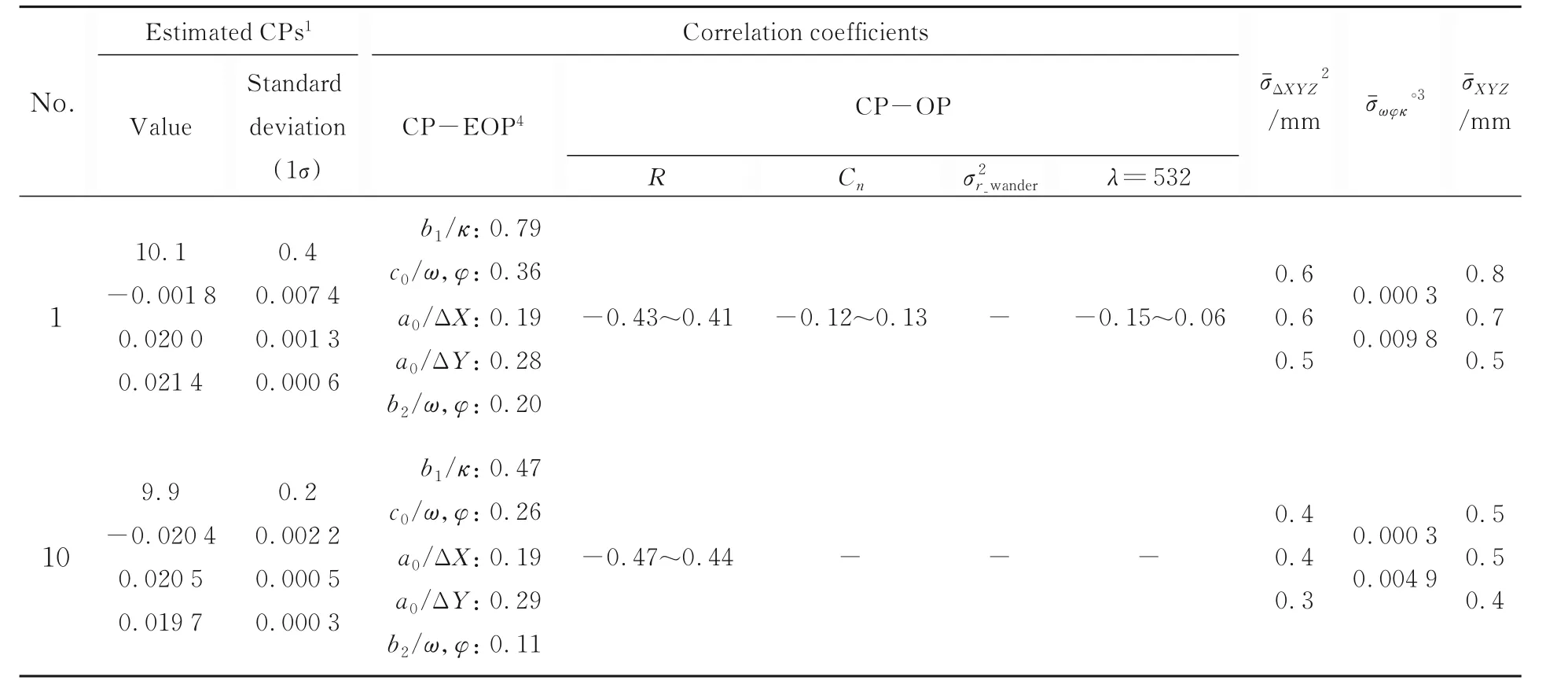
表3 无已知点参与的自检校模拟结果Tab.3 Simulation results of self-calibration without points （°）

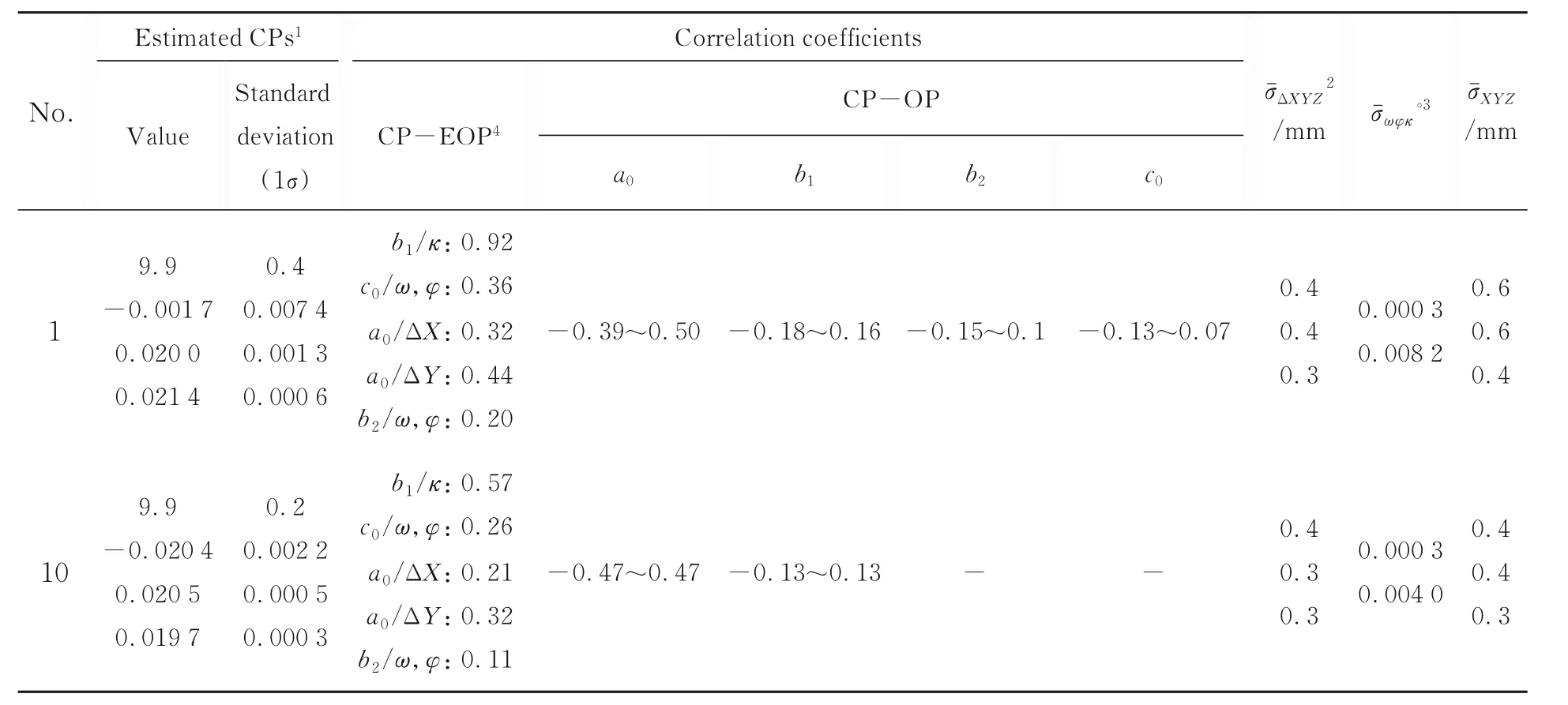
表4 包含3个已知点的自检校模拟结果Tab.4 Simulation results of self-calibration with 3 points

5.2 结果分析

由表3～表4和图3分析可知，扫描仪加常数、水平轴误差和竖盘指标差等CPs在所有模拟设计下都得到了高精度估计，其估计标准差约为其估计值的1/10，且估计值与模拟值吻合较好；在2站扫描设计下，视准轴误差b1与扫描仪方位κ高度相关（ρ约为-0.8），导致这两个参数估计结果较差。虽然通过多次扫描，b1的标准差有所下降，但并没有降低b1和κ间的相关性，同时采取不同测站高度扫描未发现对参数估计有显著影响。除b1与κ间的高相关性外，所有CP-EOP间的相关性都相对较低，且在检校中影响不显著。采用4站扫描设计显著改善了b1的估计结果（其估计标准差比2站配置下改善约2倍），且ρ下降到0.5。

分析图4可知，扫描仪中心位置的已知有助于降低a0和ΔX及ΔY间的相关性（ρ最高约为0.3）。a0和ΔY间的相关性高于它和ΔX间的相关性，这可能与外部坐标系统的Y轴沿检校场长尺寸方向有关；此外，CP-OP相关性非常低，观测到的最大相关性（0.4～0.5）存在于加常数a0和X，Y标志点坐标间。无已知点检校的最大相关系数为0.28，使用3个已知点检校的最大相关系数为0.39，以上相关性对TLS自检校而言并不算高；而OPs估计的平均标准差处于亚毫米水平，由于加常数a0和标志点X，Y轴向间的相关性相对较高，OPs平面标准差稍差于高程标准差。

最后结合图3可知，检校网中已知点的存在对CPs估计无显著影响，但对参数相关性有较大影响，如b1和κ间的相关性以及a0与ΔX，ΔY间的相关性。相对于无已知点检校实验，其相关性变大，CP-OP间的相关性也略有增加，而EOPs和OPs的标准差却略有下降。

6 结论

本文以全站仪误差模型为基础提出了一种脉冲TLS仪器系统误差自检校方法，通过对估计参数配置先验权重信息以及对检校网进行优化设计，降低了脉冲TLS自检校平差中大多数CPs和其他系统参数间（尤其是与外方位参数EOPs间）的相关性，从而提高了估计参数的可靠性。检校实验结果表明，4站扫描检校配置的设计结果显著优于2站扫描设计，而扫描仪设站的高度差异、同一测站多次扫描、正交扫描等措施并未对参数估计产生显著影响。此外，为可靠估计扫描仪加常数，需以约1 mm的高精度测定扫描仪站坐标，由此显示出采用随机内部约束方法定义检校网基准的优势。