双波长干涉显微镜波长的双约束标定
2021-07-03黄小津李璐璐
刘 乾,黄小津,李璐璐,张 辉
(中国工程物理研究院 机械制造工艺研究所,四川 绵阳621999)
1 引言
作为表面微观形貌检测的有效手段,干涉显微镜广泛应用于制造、微电子、生物等多个领域。由于干涉条纹的周期性,所得到的相位压缩在[0,2π]区间,干涉显微镜无法分辨干涉条纹的级次,因而不能分辨表面上大于半波长的高度差异。为确定干涉条纹级次,研究人员提出了相干扫描干涉和双波长(或多波长)干涉方法。前者通过扫描表面全高度范围,利用相干包络确定零级条纹而展开相位[1];后者通过比较不同波长的相位差异,采用合成较长的拍波拓展了高度范围限制[2]。这两种方法的本质都是确定条纹的级次。相较于相干扫描干涉,双波长干涉显微镜无需在表面全高度范围内扫描,具备速度快、效率高的优势。
在高度重构过程中,光波长的标定精度是双波长干涉显微镜的精度来源,因此必须对光波长进行标定。一种直接的标定方法是采用光谱仪测量光波长。对于激光光源来讲,由于激光线宽非常窄(通常在0.1 nm以下),能够很精确地确定单个光波长的平均波长,甚至可以直接以名义波长作为实际波长[3-4]。而对于宽光谱的照明(如LED作为光源),则需要采用光谱仪对波长测量后并计算中心波长[5]。此外,在数值孔径较大的干涉显微镜中,物镜出射的聚焦光线会引起倾斜效应,在标定照明波长之外还需要根据物镜的数值孔径计算倾斜因子,得到等效波长[6]。为直接溯源到长度基准上,也可以采用标准件或标准长度对波长进行标定。Liang等在三波长干涉中采用461 nm的标准台阶对三个等效波长进行严格标定,并认为滤光片带宽越窄,波长的校准精度越高[7]。郭彤等以压电陶瓷扫描器的步长作为长度基准,利用小波方法分别确定三个等效波长,可以达到1 nm的标定精度[8]。上述标定方法利用了长度基准与波长的关联,以长度整体误差的最小化为目标。然而,当前的标定方法没有考虑光波长之间的关系,而这种关系的缺失会给表面高度重构带来局部误差(如跳变点),在光滑表面测量时产生不可接受的误差,严重影响标定结果。
本文基于双波长干涉表面的高度重构误差分析,在波长与长度基准建立关联之外,增加了对光波长之间的关联,提出了一种双约束的波长标定方法。首先理论分析了高度重构方法及波长误差对表面高度重构的影响,然后介绍双约束的波长标定方法,最后以计算机仿真和实验对标定方法进行了验证。由于多波长干涉可以视为双波长干涉的拓展,因此本文主要以双波长干涉为例展开研究。
2 光波长误差对高度重构的影响
2.1 表面高度重构
两个光波长λ1,λ2对应的相位分别为φ1,φ2,假设λ1<λ2。将两个相位相减,得到差分位相ΦD′=φ1-φ2,其 对 应 的 拍 波 波 长 为ΛD=λ1λ2/(λ2-λ1)。若 表 面 总 高 度 大 于ΛD/4,则 需 要 对ΦD′在空间展开,展开后的相位记为ΦD。差分相位对应ΛD的级次为:

条纹级次MD由整数I和小数部分F组成,即M=I+F。式(1)得到级次包含了整数部分和小数部分。光相位φ2在0~2π之间,其小数部分可以简单地计算为F2=φ2/2π,但其整数部分是未知的。根据相位与波长之间的理论关系:M2λ2=MDΛD=h/2,计算表面光相位的整数部分为I2=MDΛD/λ2-F2。由于相位中含有误差,则计算的I2未必是整数,但可以通过四舍五入将它近似为整数。加上已经得到的小数部分F2,λ2相位的级次可以计算为:

这样就可以通过M2计算表面高度:

式(3)计算的表面高度是直接从光波长相位得到的,能够避免差分相位误差随波长放大。更进一步地,为了减小表面高度重构误差,可以构建波长更短的和频相位[5],即ΦS=φ1+φ2,其对应的波长为ΛS=λ1λ2/(λ1+λ2)。和频相位条纹级次的小数部分为FS=φS/2π。从光波长估算和频相位的级次:

计算表面高度为:

利用式(5)从和频相位重构的高度能够获得比单波长干涉更低的噪声[5]。
2.2 光波长误差的影响
光波长误差对表面高度重构最主要的影响体现在相对高度的缩放上,如式(3)和式(5),表面上不同点之间的高度误差与波长误差成正比。实际上,在采用式(2)和式(4)估算级次时,波长误差也会导致级次估算误差。假设光波长λi的误差为Δλi,相对误差为εi=Δλi/λi。光波长误差相互独立,通过偏微分可以计算两个合成波长的误差分别为:

根据式(2)和式(4),λ2相位、和频相位的级次估算误差e2,eS分别为:

若级次估算误差e的绝对值小于1/2,则在式(2)和式(5)的四舍五入计算时会被忽略,不会导致跳变误差;否则,将会产生级次估算误差,表现为重构表面上半波长整数倍的跳变点。为保证重构表面高度不因波长误差出现跳变点,需保证式(7)中ε1-ε2=0。该约束的物理意义是,允许标定的光波长存在一定的误差,但波长误差之比需要与真实波长比例相等,即λ1/λ2的比值应当与真实波长比值相等。
从和频相位重构表面高度的误差,对式(5)进行微分可得:
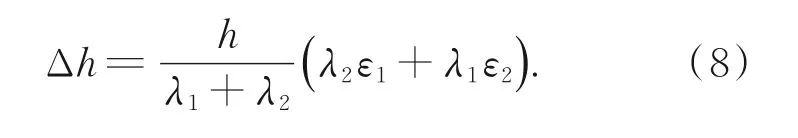
为 保 证 高 度 的 准 确 性,应 使λ2ε1+λ1ε2=0。该条件的物理意义是,若波长的相对误差与波长成反比且符号相反,则高度误差为零。
考察式(7)和式(8)发现,式(7)要求波长误差同号,而式(8)则要求二者反号。因此,跳变误差与高度误差的限定能够对光波长形成足够的约束条件,进而获得确定的波长值。
3 双约束标定方法
3.1 方法原理
为兼顾整体高度精度并抑制跳变点,本文提出一种双约束的光波长标定方法。其基本思想是:以跳变点最少的重构结果约束光波长比值,以基准长度约束光波长算术值(以和频波长为约束对象),如图1所示(彩图见期刊电子版)。该方法只需要一个台阶高度标准件(台阶高度h0应小于ΛD/2)。具体流程为:

图1 波长双约束标定原理示意图Fig.1 Principle diagram of two-wavelength constraints calibration
第1步:分别以两种光波长照明,测量标准件平面部分的光波长相位;
第2步:两个光波长在预先估计的区间λi∈[λi,min,λi,max]内变化,按照式(1)、式(2)、式(4)和式(5)进行表面高度重构,将重构平面校平,判断跳变点(高度绝对值大于ΛS/4的点),统计每种波长组合下的跳变点数量;
第3步:从跳变点最少的波长组合确定光波长的比值:

这样可以确定波长比值的约束(图1红色直线)。
第4步:分别以两种光波长照明,测量标准件台阶部分的光波长相位;
第5步:式(2)和式(4)可以转换成:

因此,根据式(10)得到的相位级次与波长无关,仅由相位和波长比值决定。按照式(5)、式(10)进行表面高度重构,得到以和频波长级次为计量单位的台阶高度M0。由此可确定和频波长的数值为:

此时,通过和频波长约束了光波长的数值(即图1的蓝色曲线)。
第6步:求解式(9)和式(11)组成的二元方程组,得到光波长的数值(图1中的交叉点)。
通过上述步骤得到的两个光波长数值具有双重约束,能够保证精确的高度溯源,同时也能避免波长标定误差。
3.2 仿 真
对光波长的标定方法在操作层面进行仿真。光源为绿光和红光,波长分别为λ1=0.523 μm,λ2=0.625μm,λ1/λ2=0.8368,合成拍波波长ΛD=3.2μm,和频波长ΛS=0.285μm。生成的相位中加入了标准差为0.03 rad的随机相位噪声。
3.2.1 确定波长比值
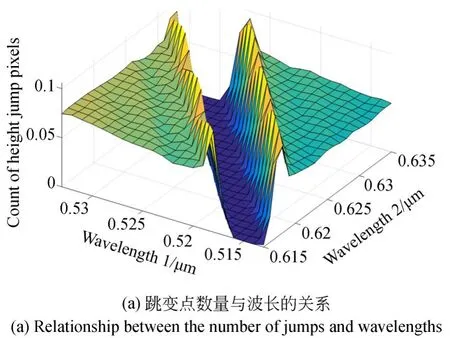
生成平面的整体高度约为7μm。在波长数值±10 nm区间内进行波长组合并重构表面高度。由于被测面为一个平面,理论上校平的平面上每点残差都应接近于零值。然而,当波长误差导致表面上存在跳变点时,校平后的表面上存在高度明显大于ΛS/2的点。作为示例,(λ1,λ2)组合分 别 为(0.515μm,0.615μm)、(0.523μm,0.622μm)时,重构并校平后的表面如图2所示。对于(0.515μm,0.615μm)的波长数值,比值r=0.8373,接近准确值,因此校平后的表面残差呈现纳米量级的随机分布,不存在跳变点。对于(0.523μm,0.622μm)的波长数值,比值r=0.8408,表面残差存在大于ΛS/2的跳变点,数量约为3.6%。得到跳变点的归一化数量与两个波长的关系如图3(a)所示。可以看出,跳变点数量最小的波长组合存在一个明显的线性关系,与理论分析完全相符。从图3(a)中寻找每一行的最小值(即跳变点数量最少的点)对应的波长组合。此例中共21个组合数据,其比值分布如图3(b)所示。虽然波长的比值有所变化,但变化不超过0.5%。此21个波长组合的波长比值平均为0.8371,与真实值0.8368相差小于0.001,表明该方法确定的波长比值具有很高的可信度。
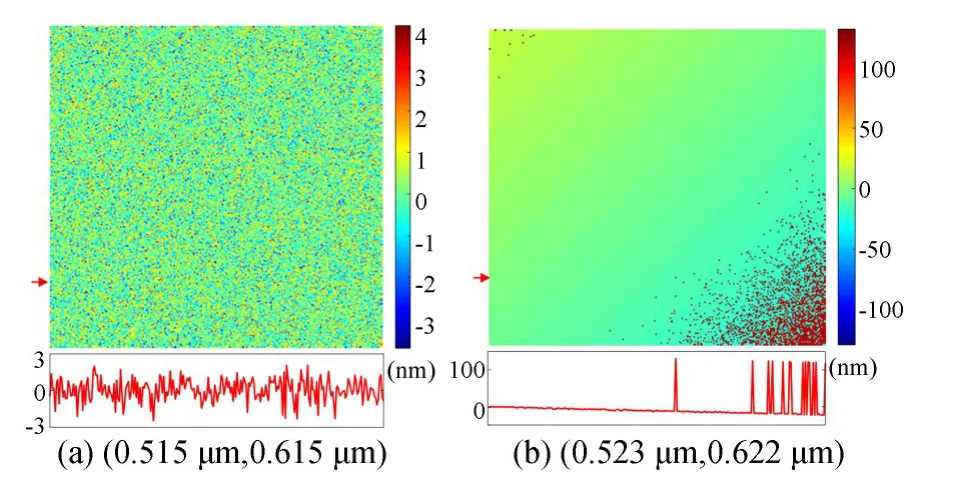
图2 两种不同波长组合重构表面的误差分布。图中轮廓为箭头所指行的数据Fig.2 Error maps of reconstructed surface with different wavelengths values.Profiles are extracted from the row indicated with arrows

图3 波长比值的仿真结果Fig.3 Simulation results of wavelength ratio
3.2.2 确定波长
以高度为0.7μm的台阶为测试表面,加入倾斜项模拟实际情况。生成光波长对应的相位,并加入标准差为0.03 rad的高斯白噪声。如果以估计的光波长数值进行表面重构,可能会因为估计的偏差导致台阶表面存在跳变点,从而影响重构的台阶高度。本方法中首先确定了波长的比值,在表面重构时不依赖具体的波长数值,从而避免台阶表面发生跳变。按照式(11)从光波长相位中重构表面,得到以和频相位级次为单位的表面高度分布,台阶的表面没有跳变点,如图4(a)所示。对台阶底面进行校平,如图4(b)所示,进行台阶上下表面高度分析,得到台阶高度为4.917。根据已知的台阶高度,通过式(11)反算和频相位波长为0.285μm。加上波长比值的约束,可以计算两个波长为λ1=0.5231μm,λ2=0.6249μm。该标定的数值与真实值仅相差0.1 nm,具有非常高的精度。

图4 重构的台阶表面Fig.4 Reconstructed step surfaces
为验证本方法的鲁棒性,通过仿真研究了波长标定结果与相位噪声的关系。标定时采用12次结果的平均值。相位噪声为高斯随机分布,以噪声的标准差表征噪声强度,得到波长相对误差与噪声强度的关系如图5所示。虽然波长标定误差随着噪声的增加而变大,但对于干涉测量来讲,0.05 rad的噪声强度已基本达到上限,此时的标定误差仍小于0.1%。这表明本方法能够容忍噪声的影响。
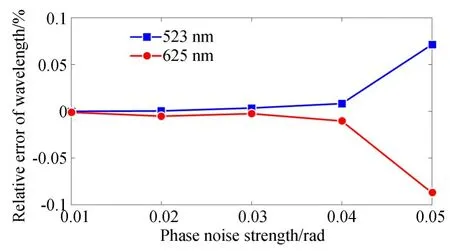
图5 波长标定误差与相位噪声的关系Fig.5 Wavelength calibration error as function of phase noise
双约束波长校准方法的精度高,其主要原因在于:(1)建立了两个约束条件限定光波长数值;(2)以更短波长的相位重构表面,有效抑制了相位误差的放大;(3)重构表面时以波长比值带入运算,避免了因波长估计偏差引起台阶表面的跳变点,保证了重构的台阶精度。
4 实验
4.1 实验条件
实验使用一台配有多光源的干涉显微镜对提出的标定方法进行了验证。干涉显微镜配有绿光和红光LED。选用20×的Mirau型干涉物镜,测试范围约为0.85 mm×0.71 mm。单个光波长照明下,每次采集9幅π/2相移干涉图。选用一种可补偿相移误差算法从单波长干涉图中提取相位,该算法能够抑制扫描器误差和环境振动对测量的影响[9]。这里将两种光波长照明下采集9×2幅干涉图并重构表面称为一次测量。作为对比,先采用光谱仪测量LED的光谱如图6所示。绿光LED光谱的半高宽约为31 nm,红光LED光谱的半高宽约为14.5 nm。采用重心法计算其平均波长分别为λ1=532.69 nm,λ2=610.92 nm。根据重心法得到波长数值,其合成的拍波波长约为4.16μm。

图6 干涉显微镜的绿光与红光光谱Fig.6 Spectra of green and red LEDs in interference mi⁃croscope
4.2 波长标定
选用一个标称1.8μm的台阶作为标定长度基准。台阶计量的高度为1.768μm±10 nm(k=2)。首先,对台阶的平面部分进行8次测量,计算得到两个光波长的相位。分别在λ1为(533±15)nm,λ2为(611±7)nm的范围内,以1 nm为间隔的波长组合对表面高度进行重构,并计算表面跳变点数量。其中一次重构表面的跳变点数量如图7(a)所示,其对应的波长比值如图7(b)所示。8次波长比值的检测结果平均值为0.8719。

图7 波长比值的标定结果Fig.7 Calibrated wavelength ratios
然后,对台阶部分进行12次测量,用于确定和频波长的数值。重构表面以和频相位的级次表示,其中一组校平后的台阶表面如图8所示。为避免台阶交界处局部不平整导致的台阶高度误差,对台阶交界处1/3之外的平面进行高度分析。12次测量得到台阶高度的平均值为11.96,那么对于式(11),M0=11.96。结合波长比例和波长算术值的约束关系,计算得到λ1′=552.9 nm,λ2′=636.6 nm。该结果与光谱仪得到的光波长偏差较明显,此偏差主要源于物镜的倾斜效应。

图8 校平后的台阶表面(a)及轮廓(b)Fig.8 Leveled surface(a)and profile(b)of step
为获得高精度结果,共标定12次并取标定结果的平均值。12次标定得到的台阶高度如图9(a)所示,除了其中一次带有明显差别(仍在3σ范围内)外,其他11次标定结果的吻合度相当高。12次得到的台阶高速平均值为11.96倍的和频波长级次。12次波长标定结果如图9(b)所示,取12次平均值得到λ1=553.5 nm,λ2=634.8 nm,标定结果的标准差均在亚纳米范围,具有非常高的精度。该标定结果与光谱仪测定的等效波长具有约2~3 nm的偏差,由此表明直接采用光谱仪进行波长标定存在明显的误差。

图9 台阶高度(a)与波长数值(b)的12次标定结果Fig.9 Calculated step heights(a)and wavelength values(b)of 12 calibrations
4.3 刻线深度测量验证
为验证波长标定效果,采用双波长干涉显微镜对一个刻线板的沟槽进行测量。对沟槽进行8次测量,采用4.2节标定的波长数值对表面高度进行重构,其中一次测量的表面高度如图10所示。在刻线板的特征标记位置处(图10(a)的箭头所指部分),沟槽的标称深度为0.7μm,其轮廓如图10(b)所示。按照3W原则对底部区域取平均,此次测量的高度为0.7533μm。8次测量结果的平均值为0.7530μm,标准差为0.38 nm,如图11所示。同时采用干涉显微镜的白光垂直扫描干涉(VSI)模式与扩展相移干涉(ePSI)模式对沟槽进行了16次平均测量,标记处的深度分别为0.7535,0.7481μm。本方法测量的沟槽深度值与两种模式测量结果的最大偏差分别为0.5,4.9 nm,表明所标定的波长数值具有非常高的准确性。

图10 测量的沟槽表面(a)与特征标记处的轮廓(b)Fig.10 Measured grooved surface(a)and profile(b)in⁃dicated with symbols

图11 沟槽深度的8次测量结果Fig.11 Measured groove depth in 8 measurements

5 结论
本文基于表面跳变误差与高度误差的约束,提出了双波长干涉测量的双约束标定方法。通过确定波长比值与波长算术关系对波长数值进行约束求解,进而得到准确的等效波长,为表面高度重构提供基础参数。标定只需要一个标准高度的台阶即可完成,但比传统的台阶高度检测多了一个约束,提高了波长标定精度。仿真与实验结果表明,波长标定精度可达到亚纳米量级,实际测量表面高度的精度优于0.5%或更高。虽然本方法只对双波长光干涉展开讨论,但也可拓展到三波长干涉,或者应用于数字全息技术。
