三维多点交会点位空间分布优化与精度分析

丁克良，靳婷婷，蒋志强，李 甜，陈昊旻

（1.北京建筑大学 测绘与城市空间信息学院，北京102616；2.中国科学院 上海高等研究院，上海201210；3.北京普达迪泰科技有限公司，北京100083）

1 引言

随着大型科学工程的不断发展，大尺寸精密工程三维控制网的测量精度越来越高［1-2］。为了保证布设的点位可以完全控制建筑的施工和移动模块的安装，测量点数量要达到数万个，而常用的三点交会法已不能满足大规模复杂工程的测量精度要求，需要对测量点和测站进行加密处理。多点交会法却可以选取有利的点位位置，有效地提高点位交会精度，从而提高整体网型的测量精度。

近年来，国内外研究人员就空间三维坐标测量精度进行了多方面的研究。张皓琳等根据最小二乘不等精度估计理论，分析得出坐标转换精度主要受测量精度及点位几何分布的影响［3］。刘湛基等提出结合最小二乘法的RANSAC快速转换算法构建公共点拟合变换模型，再利用评判模型选定最优的公共点分布结构［4］。李辉等分析了激光跟踪仪受公共点分布影响的系统误差，构建了转站参数误差补偿模型，提高了多基站转站精度［5］。王强和Bergen等利用精度因子（Dilu⁃tion Of Precision，DOP）分别研究了到达角交汇定位系统（Activity On Arrow，AOA）基于距离测量和角度测量时仪器的最佳布设位置和数量［6-7］。熊芝等比较分析了基于空间测量定位系统(workshop Measurement Positioning System,w MPS）网络布局中几种经典测站布局方式对测量精度的影响，获得了最佳站位分布结构［8］。周娜等根据激光雷达及iGPS系统的测量特性，对飞机数字化测量网络的布站进行了优化设计，有效提高了测量精度［9］。贾庆莲等基于三维几何分布 模 型（Geometrical Dilution of Precision，GDOP）分析了多个布站模式下周视搜索系统对目标的定位误差及分布规律，选定了最佳的布站模式［10］。Konchenko等通过DOP和圆误差概率（Circular Error Probability，CEP）优化了机场多边监测系统的仪器布设位置［11］。范百兴等通过构建激光干涉测量三维点坐标的几何精度因子（Position Dilution of Precision，PDOP）模型，有效避免了测量点及测站的不利测量位置［12-14］。此外，研究人员还针对全球导航定位系统中卫星分布的空间三维坐标测量精度进行了研究［15-17］。所以，对多种测量方法的点位空间分布结构的研究，是提高空间三维坐标测量精度的重点。

由于测量点的数量和空间位置分布是影响测量精度的主要因素，本文基于激光跟踪仪测量系统，在分析三维平差模型的基础上，对测量点数据进行量化分析，构建了加权精度因子模型（Weighted Dilution Of Precision，w DOP），通过多方向多距离的点位交会插点精度实验分析，选取有利的点位位置，获得了满意的测量精度。

2 多点交会的计算方法

2.1 函数模型

如图1所示，多点交会的观测值为待定点P点到n个测量点的斜距S1～Sn，天顶距β1～βn，水平方向α1～αn，观测值个数为3n，必要观测数为6。其中n为测量点个数，测量点T i的坐标为(X i，Y i，Zi)，假 定 待 定 点P改 正 坐 标 为(X p，Y p，Zp)，近似坐标为(X0p，Y0p，Z0p)，近似坐标的改正数为(δXp，δY p，δZp)。经推导，各观测值的误差方程如下［18-19］：

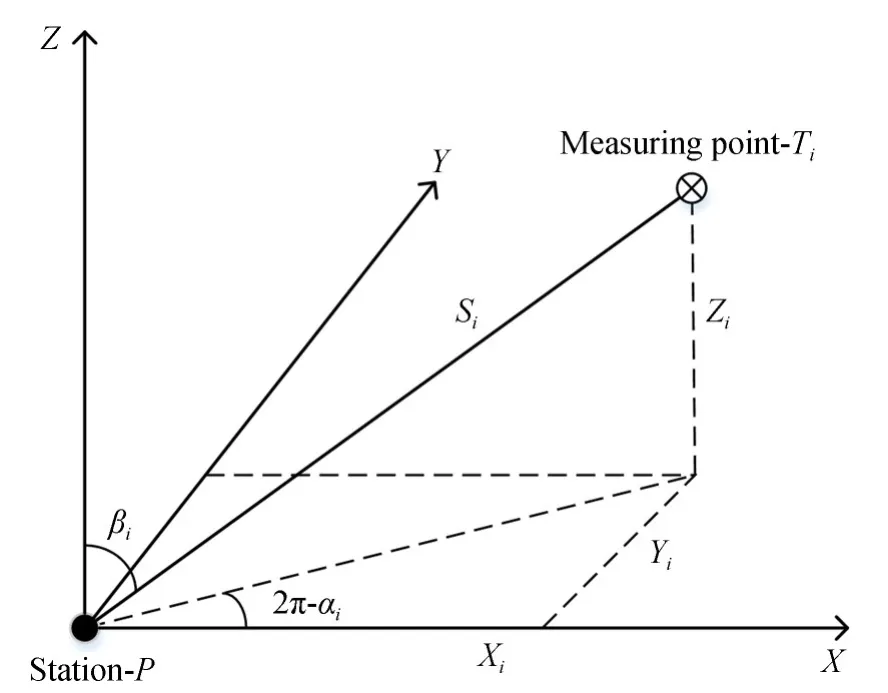
图1 激光跟踪仪测量原理Fig.1 Measurement principle of laser tracker

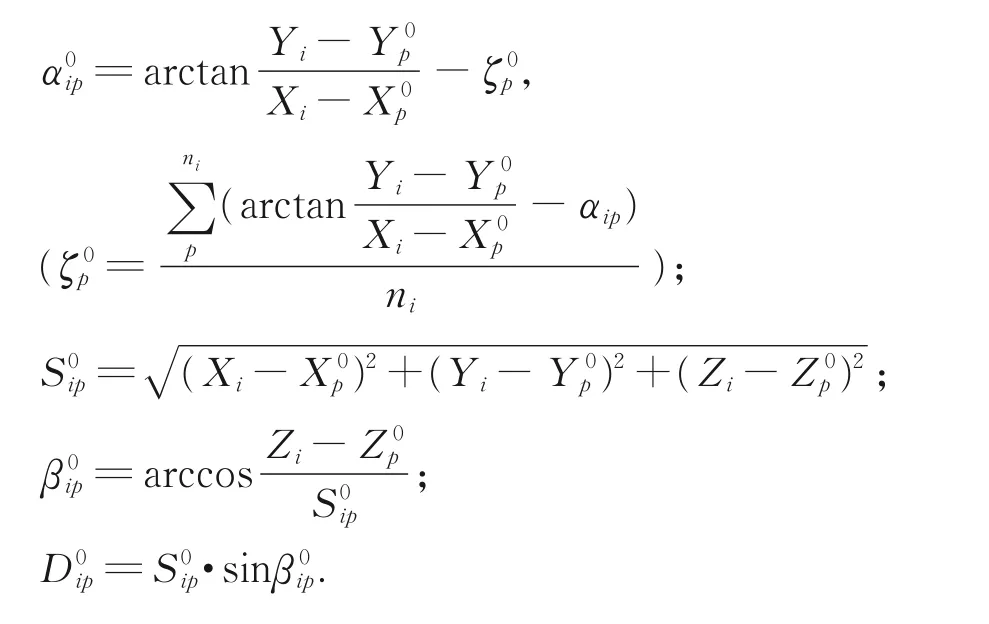
上述误差方程式表达成矩阵形式为：

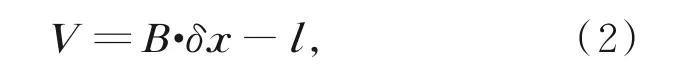
其中：

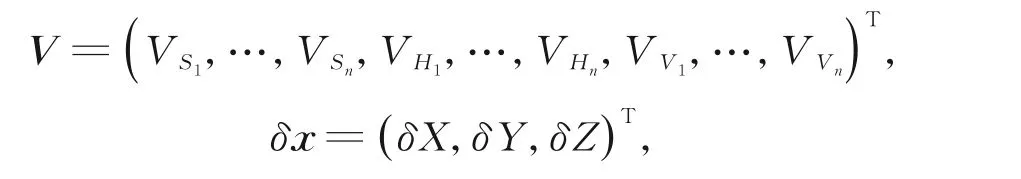
计算B，l矩阵时，ρ=206265。

2.2 观测值的权矩阵确定

以激光跟踪仪的测量数据为例，激光跟踪仪的测角误差随着测量距离的增大而增大［14］，其测角的标称方式一般采用±（a+b×S）的形式，其中a为固定误差，单位为μm，b为比例误差，单位为μm/m。以AT 960激光跟踪仪为例，其角度标称精 度 为±（15μm+6μm/m）。因 此，角 度权为［20］：

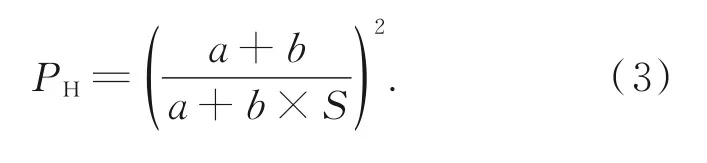
激光跟踪仪的天顶距测量精度与水平角的标称值相同，但实际测试表明，激光跟踪仪的一测回水平方向中误差要小于一测回垂直方向中误差，因此在平差解算时，可按照如下原则赋权［21］：

其中k为小于1的系数，参考AT 960激光跟踪仪的测角精度检测结果，k一般取0.7～0.8比较合适。

激光跟踪仪的距离观测值的权可以表示为：

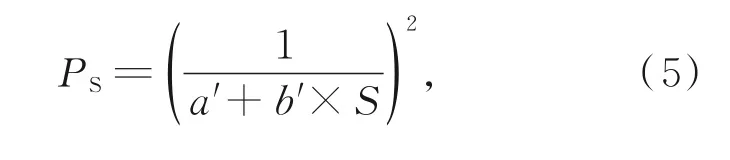
其中：a′为测距固定误差，b′为测距的比例误差，但是激光跟踪仪的测距固定误差一般都很小，因此其标称误差一般都忽略固定误差，只给出比例误差。AT 960的距离标称精度为±0.5μm/m。

2.3 加权精度因子构建

由误差方程及观测值权阵列出法方程并解算得到未知数［19，22］：

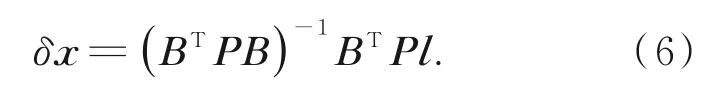
则待定点坐标为：

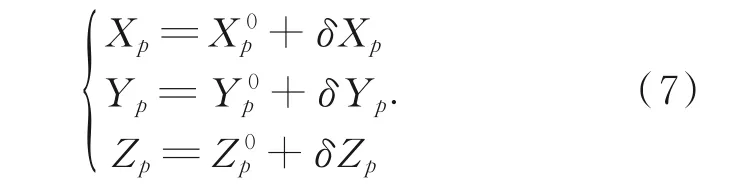
单位权中误差估值为：

式中：n为观测量个数，t为必要观测量个数。

待定点P点坐标改正数的协因数阵为：

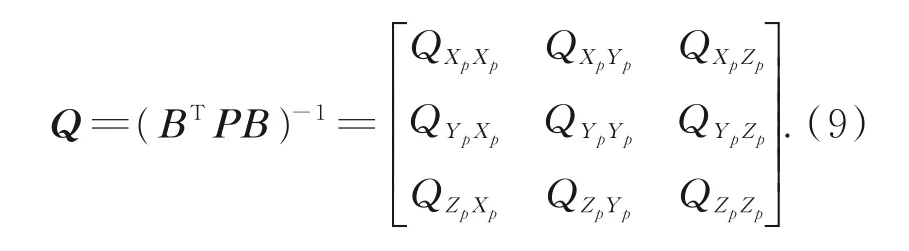
则待定点的点位中误差为：

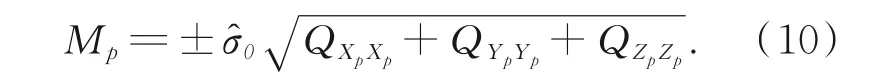
系数矩阵是测站点和测量点空间位置的反映，则加权精度因子的w DOP模型如下［16，23-24］：

其中：w PDOP为加权空间位置的精度因子，w H⁃DOP为加权水平位置的精度因子，w VDOP为加权高程的精度因子。

3 实验

3.1 实验方案

以3个测量点T1，T2，T3及测站P为基准构建四面体，由于激光跟踪仪测角误差会随距离的增大而增大，则控制水平角和天顶距固定的情况下，在P和T3的测线上，移动T3的位置，让T3方向上的距离成倍增加，分别构建T3-0～T3-15，共16个点位置，T1，T2点保持不变，如图2所示。

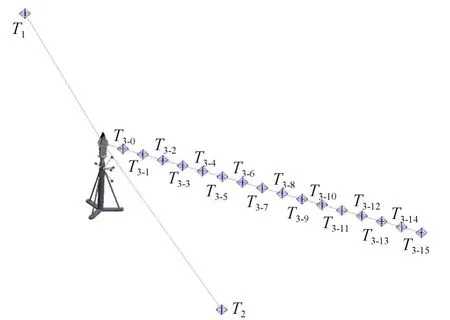
图2 点位分布Fig.2 Point distribution

对变化的四面体进行连续测量和精度计算，XOY，YOZ，ZOX面内w PDOP值的分布情况如图3所示。从图3可以看出，在3个平面内，四面体的w PDOP值均随着离测站点距离的增加而增加。所以在水平角和天顶距相当的情况下，为保证点位交会精度，测量点到测站的距离应尽量短。

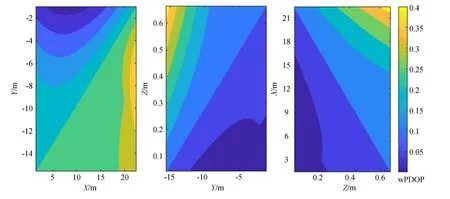
图3 XOY，YOZ，ZOX三面内的w PDOP等值线分布Fig.3 Contour distribution of w PDOP value in XOY，YOZ and ZOX planes

以某工程为例，根据已知测量点坐标，自由布设测站，以测站为原点建立坐标系，对测量点进行测量，实际布设情况如图4所示。为保证点位交会精度，剔除水平角与天顶距近似但距离较长的点，剩余点位分布如图5所示。

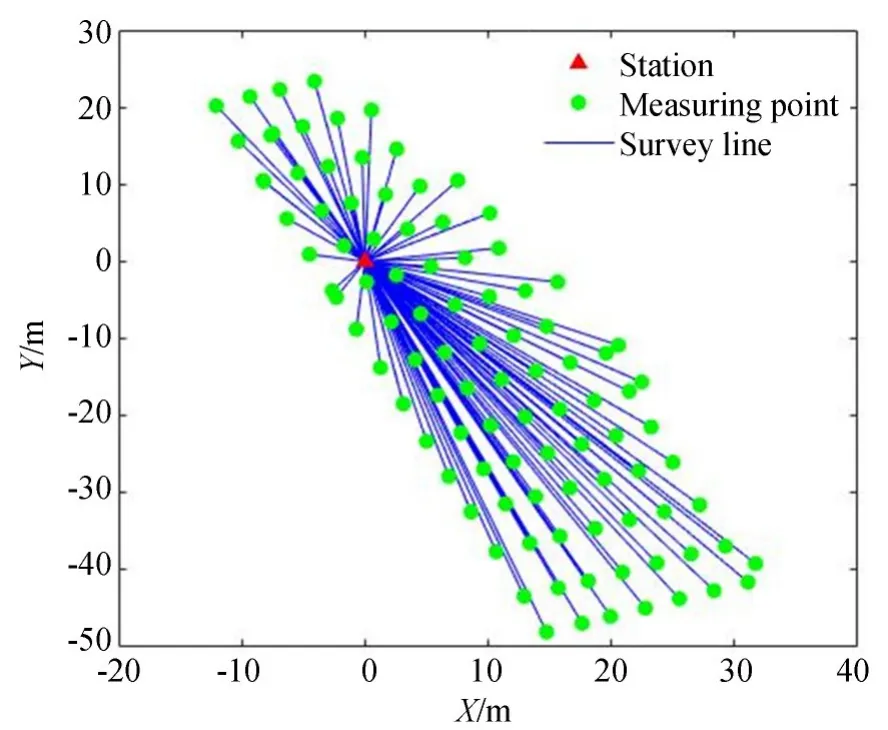
图4 原始点位分布Fig.4 Original point distribution

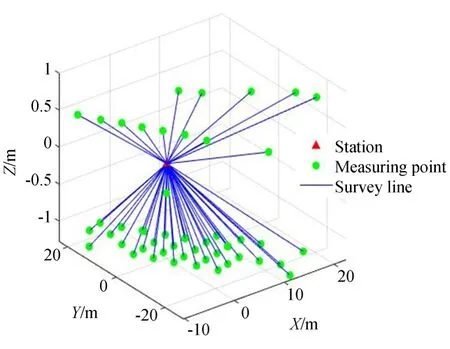
图5 抽稀后点位分布Fig.5 Point distribution after thinning

以每3个测量点为一组，对所有测量点进行排列组合，循环计算，提取其w PDOP，w VDOP，w HDOP及点位交会中误差Mp。通过实验证明w PDOP与Mp的数值分布情况基本一致，相关性达0.67，具体情况如图6所示。

w PDOP与w VDOP，w HDOP的相关性分别为0.99和0.6。从图7（a）可知，w PDOP与w V⁃DOP不仅具有良好的相关性，且w VDOP与w P⁃DOP的数值基本一致；w PDOP与w HDOP的相关性明显低于w PDOP与w VDOP的相关性，且如图7（b）所示数值上w HDOP远小于w PDOP，所以在考虑测量点的几何分布情况时，主要考虑高程方向的影响因素，即可得到较好的测量点分布结构。

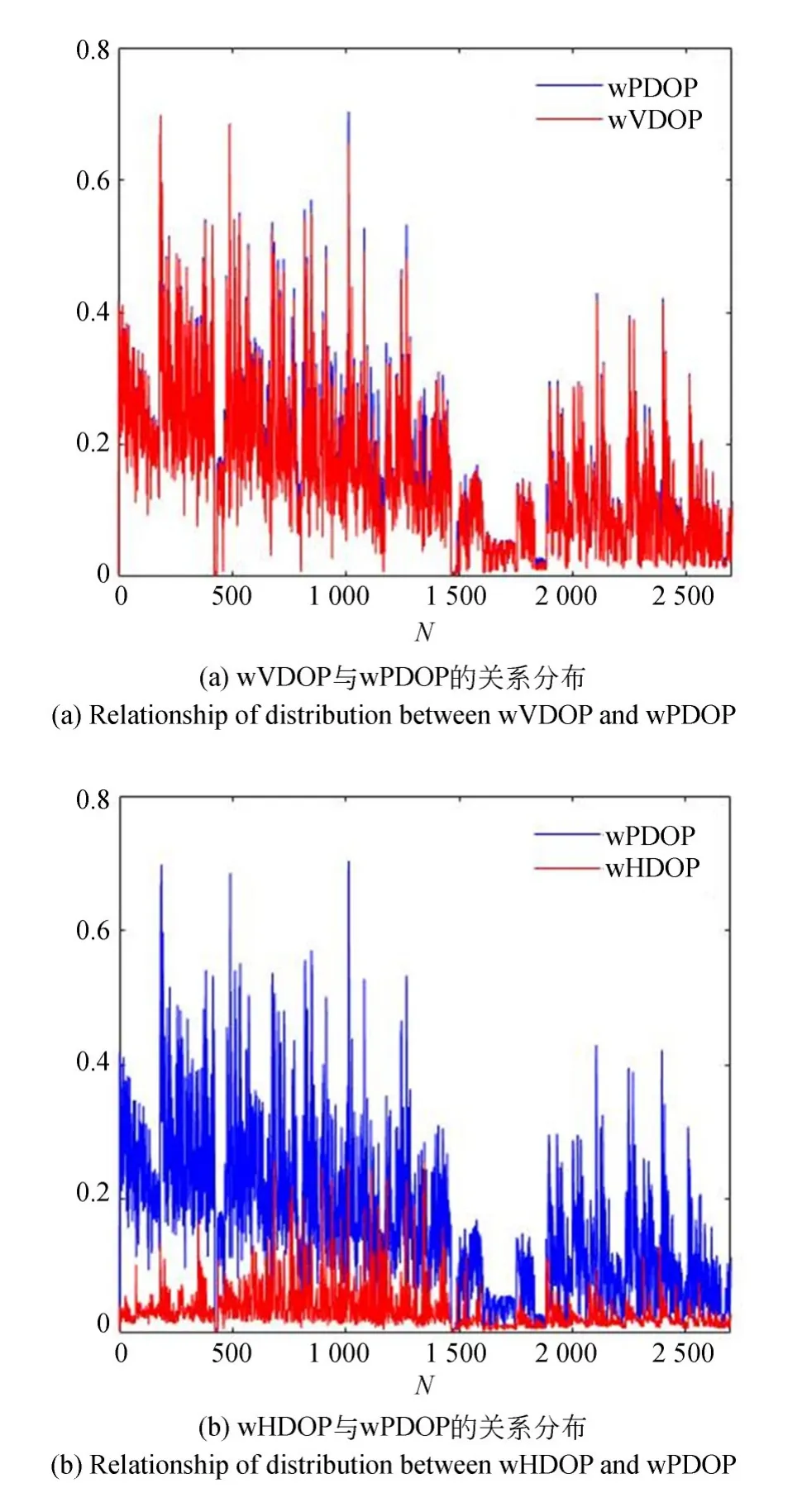
图7 w HDOP，w VDOP与w PDOP的关系Fig.7 Relationship between w HDOP，w VDOP and w P⁃DOP

w VDOP主要受天顶距和距离的影响，同组合中测量点间最大天顶距差值与w VDOP负相关，相关性达-0.60，同组合中最短距离与w V⁃DOP值呈正相关，相关性高达0.87。具体情况如图8所示，距离相同时，随着天顶距差值的不断增大，w VDOP值逐渐减小；天顶距差值相同时，w VDOP随着距离的减小而减小。所以在选择测量点时，尽量选择天顶距差值较大，测量距离较小的点组合进行点位交会，可以有效地提高点位交会精度。

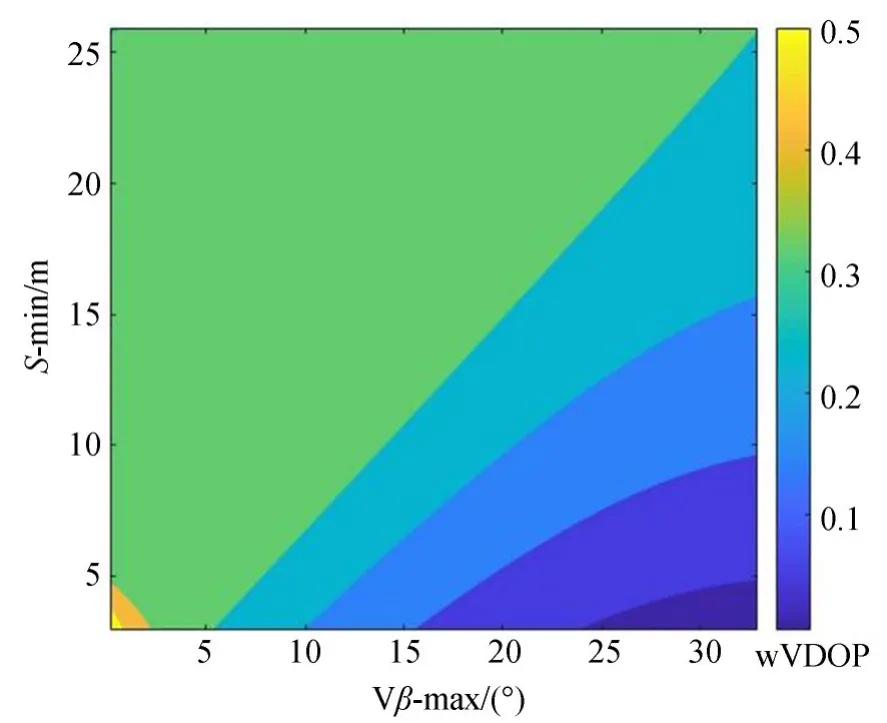
图8 距离-天顶距差值的w VDOP等值线分布Fig.8 Contour distribution of w VDOP for distance-ze⁃nith distance difference

3.2 点数及空间分布对精度影响分析

理论上，对空间点进行三维交会测量时，测量点数与测量点分布都直接影响w PDOP值。选择上述测量点较为分散的四面体组合作为基准，增加一测量点，分别计算新增测量点增加在已有四面体内部、面上、外部（增加/不增加天顶距最大差值）时对点位交会精度的影响，然后依次在4，5，…，8多面体的4个位置分别增加测量点，从而得到点位交会精度，如图9所示。整体而言，当测量点增加在多面体内部时，w PDOP值及点位交会中误差Mp最小；随着测量点数的增加，w P⁃DOP值与点位交会中误差都逐渐减小。实验证明：随着测量点的增加，点位交会精度逐渐提高；在已有多面体的内部增加测量点能更好地提高多点交会精度。

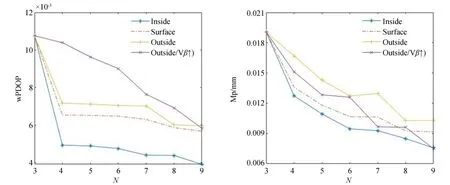
图9 多面体新增点位置与精度关系Fig.9 Relationship between accuracy and position of new points in polyhedron

在已知四面体内增加测量点，控制测量点的水平角和天顶距近似相同，增加斜距，分析结果如图10（a）所示，随着距离的增加，w PDOP值随之下降；控制测量点的距离和天顶距近似相同，改变水平角，分析结果如图10（b）所示，w PDOP值与水平角的分布没有直接关系；控制测量点的距离和水平角近似相同，改变天顶距，分析结果如图10（c）所示，w PDOP值随着天顶距的增大而减小。实验证明：在多面体内增加测量点时，在水平角一定的情况下，应尽可能地减小测量点到测站的距离、增加测量点的天顶距，从而提高点位交会精度。

图10 w PDOP与内插点位置的关系Fig.10 Relationship between w PDOP and interpolation point position

在已知四面体内依次插入1，2，…，16个点，16个点分别进行随机ξ排序，按照水平角α、天顶距β、斜距S大小降序排列，对4种排序数据进行分析，分析结果如图11所示。w PDOP值、w H⁃DOP值、w VDOP值及点位交会中误差Mp均会随着测量点数的增加而减小，在5个测量点以后数值的减小幅度逐渐降低，6个测量点时均可得到一个较稳定数值。所以，在点位交会中，使用6个点进行交会计算，即可得到较高、较稳定的点位交会精度。

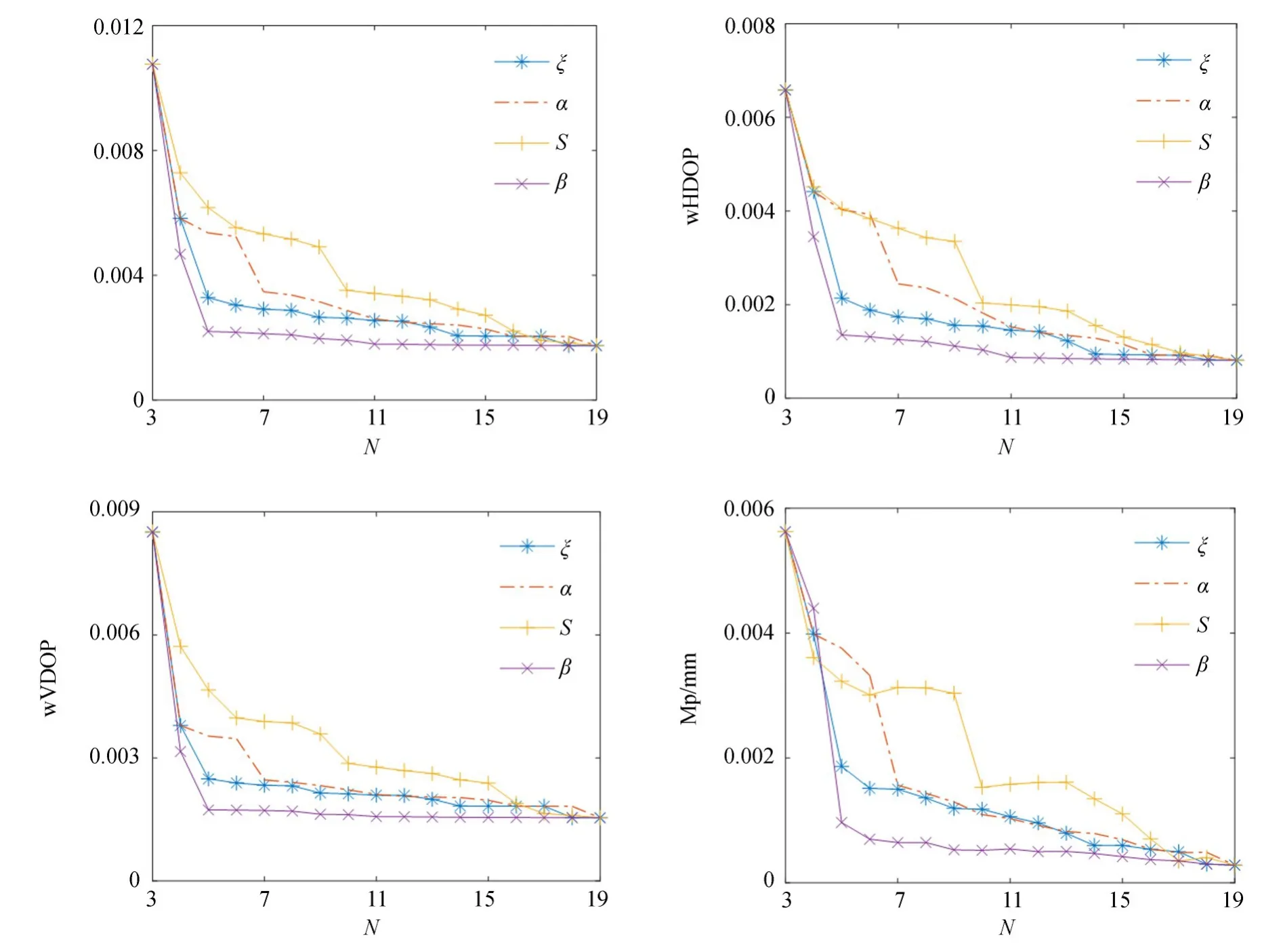
图11 多测量点交会精度分析Fig.11 Accuracy analysis of multi-measurement point intersection

4 结论

由于测站的点位交会精度主要受测量点空间几何分布的影响，本文构建了基于激光跟踪仪测量系统的w DOP解算模型，从测量点在水平面和高程方向的点位分布、测量点数量对空间点位交会精度的影响进行了比较分析。理论分析和实验表明，三点交会测量时，测站交会精度主要受点位高程方向的分布影响，高程精度因子w VDOP与空间位置精度因子w P⁃DOP值的相关性高达0.99，交会精度随着测量点间最大天顶距差值的增大和最短距离的减小而提高。当新增测量点在原有四面体之内时，对减小测量点的w PDOP值具有显著作用，且新增测量点的距离越短、天顶距越大，点位交会精度越高。增加测量点可以有效提高点位交会精度，当测量点达到6个时，点位交会精度可达到一个较稳定、较高的状态；随着测量点的增加，点位精度提高的幅度逐渐减小。

根据本文构建的几何精度因子模型w DOP值的空间分布影响因素，可以指导大尺度精密工程三维控制网布设和测量，优化最佳测站位置，最大限度地提高点位交会精度。