基于改进MOEA/D的复杂制造过程关键质量因素识别*

李岸达，张 阳,b，刘晓杰,b

(天津商业大学 a.管理学院；b管理创新与评价研究中心，天津 300134)

0 引言

复杂产品结构复杂、零部件众多，其复杂制造过程包含大量影响产品质量的潜在因素(包括过程参数、零部件尺寸参数等)。从大量潜在因素中识别显著影响产品质量的关键因素，是复杂产品质量改进和控制[1-2]前中的关键步骤。近年来，智能传感器、智能制造等技术的应用极大降低了制造过程数据的收集难度，为识别关键质量因素奠定了数据基础[3]。如何构建针对大规模、高维制造过程数据的关键质量因素识别方法成为近年来质量工程领域关注的热点问题。

特征(变量)选择是数据挖掘和机器学习领域的重要降维方法，该方法能够有效识别影响类标签的关键特征(变量)[4-6]。由于能够有效处理高维数据，近年来部分学者构建了基于特征选择的关键质量因素识别方法[7-12]。特征选择模型可构建为最大化特征对类标签预测性能和最小化特征数的多目标优化问题。基于该思路，文献[10]构建了最大化质量因素对产品质量预测精度和最小化质量因素数的关键因素识别模型。然而，该模型没有考虑制造过程数据的非平衡性(生产线收集的不同质量水平产品的数量不平衡)。针对此，文献[11]将识别模型构建为最大化分类性能指标“G-mean”和最小化质量因素数的优化问题，并采用改进多目标直接搜索(Improved Direct Multisearch, IDMS)算法求解模型。然而，IDMS算法收敛速度较慢，如何针对识别模型构建快速高效的多目标优化算法值得进一步研究。

基于分解的多目标进化算法(Multi-Objective Evolutionary Algorithm Based on Decomposition, MOEA/D)[13]具有收敛速度快、所得非支配解集分布均匀等优点。同时，与经典的多目标进化算法NSGA-II相比，其时间复杂度更低。因此，构建基于MOEA/D的复杂制过程关键质量因素识别方法值得研究。

基于以上分析，本文拟构建基于改进MOEA/D算法的关键质量因素识别方法。该方法采用了针对非平衡制造过程数据的关键质量因素识别模型，并采用改进MOEA/D算法求解模型。改进MOEA/D采用了一种新的基于信息增益(Information Gain, IG)的种群初始化方法和一种平衡的变异方法，以改进算法针对特征选择问题的优化性能。

1 关键质量因素识别模型

假定DM×(D+1)为生产线收集的一组复杂制造过程数据。该数据包含M个产品(样本)、D个质量因素(特征)Q={q1,q2,...,qD}，以及一个质量水平变量(类标签)C∈{-1,+1}。其中“-1”和“+1”分别表示多类产品(如一般质量/合格)和少类产品(如高质量/不合格)对应的质量。关键质量因素识别可以定义为选择一个特征子集Qs⊆Q，以最大化Qs对产品质量的预测效果和最小化质量因素数的多目标特征选择问题。通常，制造过程数据是非平衡的。因此，本文采用文献[11]所用G-mean指标度量Qs对产品质量的预测性能。在二分类问题中，敏感性(Sensitivity)和特异性(Specificity)分别衡量对少类样本和多类样本的分类效果。G-mean指标为敏感性指标和特异性指标的几何平均，定义如下：

(1)

由于低敏感性或低特异性都会显著降低G-mean值，因此该指标能够有效衡量非平衡数据条件下的产品质量预测性能。

基于以上分析，本文将关键质量因素识别构建为最大化G-mean指标和最小化质量因素数的多目标优化问题，具体如下所示：

minf1=1-G-mean(Qs)
minf2=|Qs|/D
s.t.Qs⊆Q,Qs≠∅

(2)

其中，G-mean(Qs)表示质量因素集Qs所得G-mean指标值，|Qs|/D表示所选质量因素数占所有质量因素的比例。在对式(2)进行优化时，本文采用特征选择包裹(Wrapper)框架中常用的内部5折交叉验证法[5]估计G-mean(Qs)的值。

2 改进MOEA/D算法

2.1 算法总体步骤

本文提出改进MOEA/D算法求解式(2)所示识别模型。改进MOEA/D算法流程如图1所示。MOEA/D的总体思路是将原多目标优化问题，分解为N个子单目标优化问题gte(X|λi,z)(i=1,...,N)，各子优化问题由权重向量λi和理想点z决定，通过优化子问题，群体在迭代过程中能够不断进化。根据图1，算法总体步骤如下：首先，初始化N个个体(解)，并基于初始群体得到一组初始非支配解Ω。其次，针对每个权重向量λi计算规模为K的权重索引集合Bi，该集合确定了与该权重向量最近的K个权重向量和对应个体。接着，在算法迭代过程中，从各集合Bi所确定的个体中，选取两个个体并基于遗传算子(交叉、变异)产生新的个体X′。新个体X′能够对理想点Z、集合Bi确定的一组个体、以及非支配解集Ω进行更新。其中，对Bi确定的个体Xj(j∈Bi)的更新基于子优化问题gte(X|λj,z)。若新个体X′取得更小的目标函数值，则用X′替换当前个体Xj。 最后，在算法达到迭代次数T之后，输出最终非支配解集Ω。

与传统MOEA/D相比，改进MOEA/D使用了一种基于信息增益的群体初始化方法，该方法能够基于信息增益得到更高质量的初始群体。此外，针对关键质量因素识别问题，改进MOEA/D采用一种平衡变异算子，以提高算法过滤非关键质量因素的效率。

输入：群体规模N，迭代次数T，N个均匀分布的权重向量λ1，…，λN，近邻权重向量规模K；

输出：非支配解集Ω；

1 初始化群体X1,X2,…,XN并计算目标函数值(f1(Xi)，f2(Xi))，i=1,2，…，N，将群体中的非支配解添加到Ω，；

2 计算权重向量之间的距离，针对每个权重向量λi，令Bi={ii，…，ik}，其中λi1，…，λik为与该权重向量最近的K个向量；

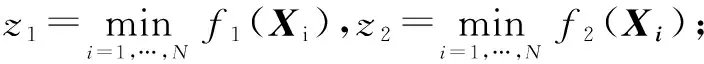
4 fori←1，…，Ndo

5 随机选择两个个体Xia和Xib(ia∈Bi，ib∈Bi)并使用遗传算子产生新的解X′；

6 更新理想点z=(z1,z2)，z1=min(z1，f1(X′))，z2=min(z2，f2(X′))；

7 foreachj∈Bido

8 if gte(X′ | λj，z)≤gte(Xj|λj，z)then

9 令Xj=X′；

10end

11 end

12 使用X′对Ω进行更新；

13 end

14 return 非支配解集Ω；

图1 改进MOEA/D算法流程

2.2 问题分解方法：切比雪夫法

令λ1,...,λN为N个权重向量，z=(z1,z2)为理想点，则切比雪夫法(Tchebycheff Approach)将多目标优化问题分解为N个子单目标优化问题。对于第j个单目标优化问题，其定义如下：

(3)

其中，X表示解，λj ,o表示权重向量λj的第o个分量，fo表示原多目标优化问题中的第o个目标函数。

2.3 解的编码

采用二进制编码，将Qs编码为一个D维向量X=(x1,x2,...,xD),其中D为原质量因素数。X中的每个元素xi(i=1,...,D)取值为1或0，其中1表示第i个质量因素qi被选择，0表示第i个质量因素未被选择。

2.4 基于信息增益的初始化方法

信息增益是基于信息熵理论的一种重要指标，该指标能够度量两个随机变量之间的相关程度[14]。假定X和Y为两个随机变量，则给定Y之后X的信息增益定义为:

(4)

其中，xi和yj为随机变量X和Y的观测值。式(4)前一项表示X的信息熵，后一项表示给定Y后的条件信息熵，信息增益被定义为两者之差。

令式(4)中的X和Y分别为质量因素qi和质量水平变量C，则可以计算每个质量因素给定质量水平变量后的信息增益IG(qi,C)。因此，信息增益能够度量质量因素与产品质量水平的相关程度。基于此，本文提出基于信息增益的群体初始化方法。该方法的思路是基于信息增益值初始化解X=(x1,...,xD)中的xi(i=1,...,D)。若IG(qi,C)较大则以较大概率初始化xi为1，反之亦然。该初始化方法具体步骤如下。

首先，计算各质量因素的信息增益IG(qi,C)(i=1,...,D)。接着，采用最大最小归一化方法将各因素的信息增益值转换为0～1之间的权重值wi(i=1,...,D)。再次，将各权重值转化为取值为[βl,βu]的初始化概率值pi，定义如下：

pi=βl+wi(βu-βl)

(5)

最后，以概率pi初始化xi为1(否则为0)。

采用以上方法，MOEA/D中个体X的每个元素不再以0.5的概率被设置为1或0。拥有更高信息增益的元素能够以更高概率设置为1。该设置有助于提高初始群体的质量，进而提高算法收敛速度。参照分位数的划分规则，本文设置 [βl,βu]=[1/4,3/4]。另外，群体多样性也是影响 MOEA/D性能的关键要素。为了在提高初始群体质量的同时保证群体多样性，群体中N/2个体基于信息增益方法初始化，其他个体仍然采用传统随机初始化的策略。

2.5 遗传算子

MOEA/D采用遗传算子产生新的个体。遗传算子包括交叉算子和变异算子。改进MOEA/D中仍采用常用的单点交叉算子。传统变异算子中，个体中每一元素以相同概率pc随机进行变异，如果该元素当前为1，则变异为0，反之亦然。然而，当个体中取值为0的元素多于取值为1元素时，传统变异算子会倾向于将更多0变异为1，导致个体选择质量因素数的增加。这种趋势不利于算法高效过滤非关键质量因素。

针对以上问题，本文提出平衡变异算子用于改进MOEA/D，该变异算子流程如下。给定个体X=(x1,...,xD)，ρ1和ρ0为两个集合，分别存储X中取值为1和取值为0的元素序列号，即xi=1(∀i∈ρ1)，xj=0(∀j∈ρ0)。平衡变异算子首先以概率pc确定个体是否变异。如果变异，则以0.5的概率从集合ρ1或ρ0选择元素进行变异，将个体变异为Xm，定义如下：

(6)

其中，r为[0,1]之间的随机数，i和j为从ρ1和ρ0随机选择的两个值。可以看到，基于平衡变异算子，个体元素“由0变异为1”和“由1变异为0”的概率是相等的，总体上该变异算子能够保证群体中的解更加平稳变异，能够解决传统变异算子的缺点。

3 实验设置

选取3组常用复杂高维制造过程数据验证改进MOEA/D，分别为SPIRA、LATEX和ADPN[7, 10]。3组数据的具体信息如表1所示。同时，选取5个特征选择算法作为对比方法，包括NSPSOFS[6]、CMDPSOFS[6]、NSGAII-IPM[10]、SFS[5]、SBS[5]。SFS和SBS为基于序列向前和向后搜索的经典特征选择算法。NSPSOFS和CMDPSOFS是最近提出的基于多目标粒子群优化的特征选择算法。NSGAII-IPM为近期提出的基于改进NSGA-II的关键质量因素识别算法。该算法在用NSGAII识别出一组非支配解之后，基于理想点法(Ideal Point Method, IPM)选择最终解。为了便于比较，改进MOEA/D、NSPSOFS和CMDPSOFS同样采用IPM选择最终解(关键质量因素集)。改进MOEA/D、NSPSOFS、CMDPSOFS和NSGAII-IPM中使用相同的群体规模N=100和迭代次数T=100以保证实验公平性。改进MOEA/D采用的交叉和变异概率为pc=pm=0.9，参数K=10[13]。SFS和SBS使用Weka[15]数据挖掘工具中的默认设置。NSPSOFS、CMDPSOFS和NSGAII-IPM中的其他设置与原文献保持一致。

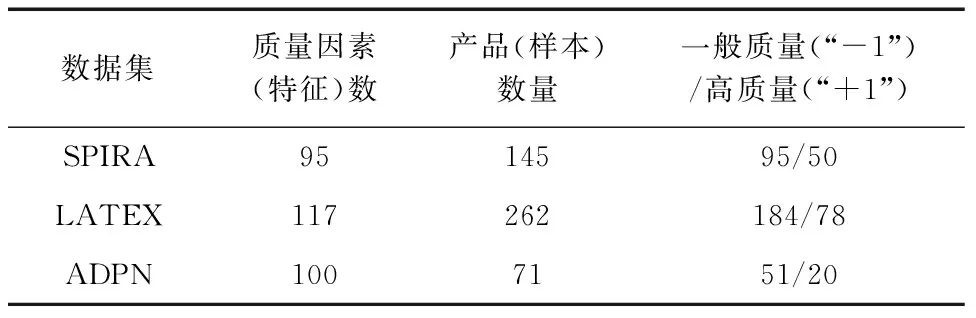
表1 数据集信息

采用分层10折[16]交叉验证法进行实验。该方法基于原数据集生成10对训练集(Training Set)和测试集(Test Set)。各特征选择算法基于训练集识别关键质量因素，所识别质量因素对测试集中产品质量的预测效果可以用于验证算法性能。重复3次10折交叉验证以产生30组实验结果，30组实验的平均结果用于比较算法性能。所有特征选择算法使用一种简单、高效的分类器——朴素贝叶斯[17]。实验所用设备为一台具有3.6 GHz的CPU和16 GB内存的个人计算机。SFS、SBS和朴素贝叶斯分类器从Weka工具调用，其他算法在MATLAB中实现。采用三类指标验证各算法有效性，分别为预测性能指标、特征过滤性能指标和运行时间指标。预测性能指标采用分类精度、敏感性和特异性综合度量所识别关键质量因素对产品质量的预测性能；特征过滤性能指标采用所选质量因素数；运行时间指标能够反映各算法的时间复杂度。

4 实验结果

表2所示为各算法识别关键质量因素基于测试集所得的分类精度结果，平均行所示为各算法在三个数据集的平均结果。可以看到，在SPIRA数据集SFS得到最高分类精度82.81%，改进MOEA/D得到略低于SFS的分类精度79.64%，其他对比算法所得结果都低于改进MOEA/D。在LATEX和ADPN数据集，改进MOEA/D能够得到高于其他各算法的分类精度，分别为80.93%和81.40%。平均结果同样表明MOEA/D得到高于对比算法的分类精度结果。综合来看，改进MOEA/D能够取得不错分类精度结果。

表3和表4所示为各算法所得敏感性、特异性结果。敏感性和特异性分别反映质量因素对少数的“高质量”产品和多数的“一般质量”产品质量的预测效果。根据表3，在SPIRA数据集，改进MOEA/D(68.00%)获得略低于SFS(74.00%)和高于其他算法的敏感性精度。在LATEX和ADPN数据集，改进MOEA/D所得敏感性精度显著高于对比算法。此外，改进MOEA/D得到高于对比算法的平均敏感性结果。根据表4，尽管改进MOEA/D在三个数据集都未能得到最高特异性精度，但总体能够得到较高水平的特异性结果。此外，改进MOEA/D得到83.58%的平均特异性精度，略低于NSPSOFS取得的最佳结果86.64%。综合来看，改进MOEA/D能够取得显著高于对比算法的敏感性结果和接近对比算法的特异性结果。这表明改进MOEA/D显著提高了对少数“高质量”产品的预测效果，意味着其能够更为准确识别关键质量因素。

表2 各算法所得分类精度结果(%)

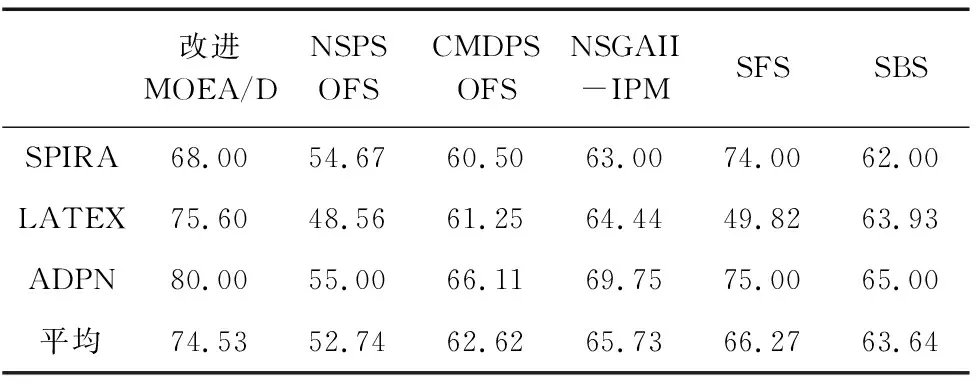
表3 各算法所得敏感性结果(%)

表4 各算法所得特异性结果(%)

表5所示为各算法30次实验所得平均关键质量因素数。可以看到，在SPIRA数据集改进MOEA/D识别了4.1个质量因素，略多于 NSGAII-IPM(3.6)和SFS(3.5)。在LATEX和ADPN数据集，改进MOEA/D分别识别4.5和2.4个关键质量因素，少于各对比算法。综合来看，改进MOEA/D在三个数据集能够得到较少质量因素，表明该算法能够有效过滤无关质量因素。

表6列出了各算法30次实验的平均CPU运行时间。综合来看，SFS整体上需要最少的运行时间，而SBS所需运行时间显著多于其他算法。这与SFS和SBS的序列向前、向后搜索策略有关。由于搜索过程中SFS逐步正向添加质量因素，算法运行过程中所需评估的质量因素集通常较小，这就明显降低了质量因素重要性评估过程所需时间。而SBS需从完整的质量因素集开始逐步剔除因素，因而在运行过程中所需评估的质量因素集通常明显大于其他算法，导致需要最多运行时间。比较基于多目标优化策略的各识别算法，改进MOEA/D的运行时间显著低于NSPSOFS、CMDPSOFS和NSGAII-IPM，表明了其具有较好的时间效率。

表5 各算法所识别关键质量因素数

表6 各算法CPU运行时间(s)

综上所述，改进MOEA/D能够有效针对非平衡制造过程数据识别关键质量因素。算法在高效过滤质量因素的同时，获得了高水平的产品质量预测效果。同时，实验结果也表明改进MOEA/D具有不错的时间复杂度。

5 优化性能分析

本节将传统MOEA/D应用于式(2)所定义关键质量因素识别问题，对比改进MOEA/D和传统MOEA/D的优化性能。对比实验仍采用表1所示数据集。两个算法在30次实验中所获得的非支配解集被用来进行性能对比。性能指标选用逆世代距离(Inverted Generational Distance, IGD)和超体积(Hypervolume, HV)[18]。IGD越小越好，HV越大越好。

表7所示为改进MOEA/D与传统MOEA/D在30次实验中所得平均IGD和HV结果。可以看到，改进MOEA/D在三个数据集都能得到比传统MOEA/D更低的IGD值。同时，改进MOEA/D在三个数据集得到比传统MOEA/D更高的HV值。以上结果表明改进MOEA/D同时获得更好IGD和HV结果。因此，针对所提多目标关键质量识别模型，改进MOEA/D具有比传统MOEA/D更好的优化性能。

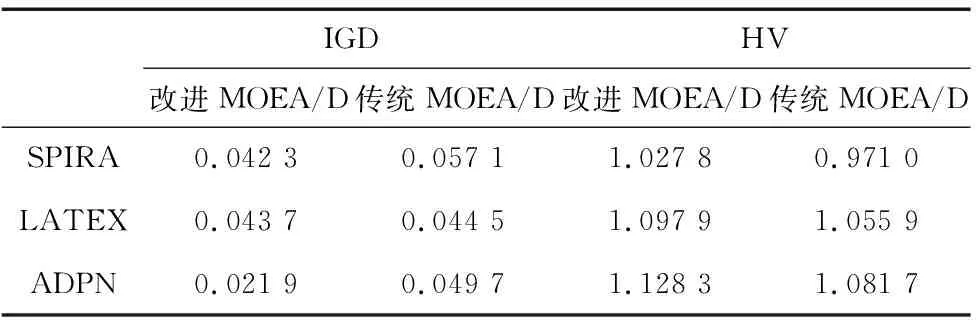
表7 改进与传统MOEA/D算法优化性能对比

6 结论

识别复杂制造过程中影响产品质量的关键因素是质量控制和改进前的关键步骤。本文构建了针对非平衡制造过程数据的关键质量因素识别模型，并提出多目标优化算法“改进MOEA/D”求解模型。实验结果表明所提改进MOEA/D能够有效识别关键质量因素，同时算法具有较低时间复杂度。进一步性能分析表明改进MOEA/D具有比传统MOEA/D更佳的优化性能。实际制造过程反映产品质量的变量可能为连续变量。因此，针对输出为连续质量水平变量的制造过程，构建关键质量因素识别方法是未来研究方向。