基于改进量子遗传算法的机械臂轨迹优化
2021-07-02周晟
周 晟
(武警士官学校基层后勤管理系被装教研室,杭州 310000)
0 引言
工业化生产的日益精进使得机械臂在日常生产、生活中的使用越来越宽泛,合理优化机械臂末端执行器运行轨迹利于提高机械臂整体工作效率,降低运行过程中的振动冲击,保障运行的稳定性和准确性。
文献[1]选取线性插值法优化四足机器人路径空间,抽取关节特征数据后,采用粒子群智能优化算法进行自适应性优化设计,提升全局路径运行空间的轨迹平稳性[1]。文献[2]立足于控制准确性和稳定性,合理设置插补算法提升末端执行器轨迹运行平稳性,降低末端执行器实际运行轨迹与理论运行轨迹的偏差数值,提升控制准确率[2]。文献[3]构建七自由度冗余机械臂虚拟样机模型,以机械臂运行过程中振动冲击最低,运行速度最高,消耗能源最少为目标,选取异类粒子群算法完成优化设计,获取单目标优化和综合优化结果[3]。
文中在量子遗传算法基础上,引入多算子协同变异机制,逐渐增加个体的变异概率促使算法跳出局部最优解。设定自适应动态旋转角步长调整机制,保障量子旋转门旋转角θi实时更新迭代,确保算法优化全程阶段具有良好的种群多样性,提高算法搜索全局最优解的稳定性。文中借助MATLAB工具箱,以串联机械臂为对象,获取光滑平顺的关节角位移、角速度、角加速度,验证改进量子遗传算法轨迹优化的有效性和可靠性。
1 机械臂轨迹规划
1.1 模型构建
文中选取串联机械臂为优化对象,合理设置相关参数,以运动学理论为基础绘制D-H参数,如表1所示[4-5]。

表1 D-H参数表
其中,αi表示连杆扭曲;ai表示连杆长度;di表示连杆偏置;θi表示关节转角。
借助MATLAB工具箱,编写串联机械臂轨迹规划平台,其控制界面如图1所示。
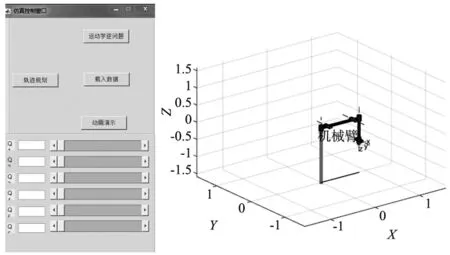
图1 串联机械臂轨迹规划平台
依据串联机械臂轨迹规划平台,验证正、逆解求解的正确性,保障轨迹规划的合理性有效推动末端执行器运行轨迹优化设计。
1.2 多项式插值
任意曲线段节点之间可运用五次多项式样条插值函数拟合构造,对构造函数求解一阶、二阶导函数可获取末端执行器关于时间t的速度、加速度表达式如式(1)所示。

(1)
式中,与起始时间点和终止时间点t0、tf对应的角位移θ0、θf为已知,且满足条件如式(2)所示。
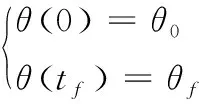
(2)
依据式(3)合理设置轨迹运行初始点、终止点的速度、加速度。

(3)
已知每个点的角位移值,设定其角速度和角加速度为0,由两点可获取6个已知条件,借助式(1)可求解所需未知系数。
机械臂连杆模型在满足无碰撞条件下,运用五次多项式插值方法结合MATLAB模拟平台,构建机械臂末端执行器运行轨迹如图2所示:
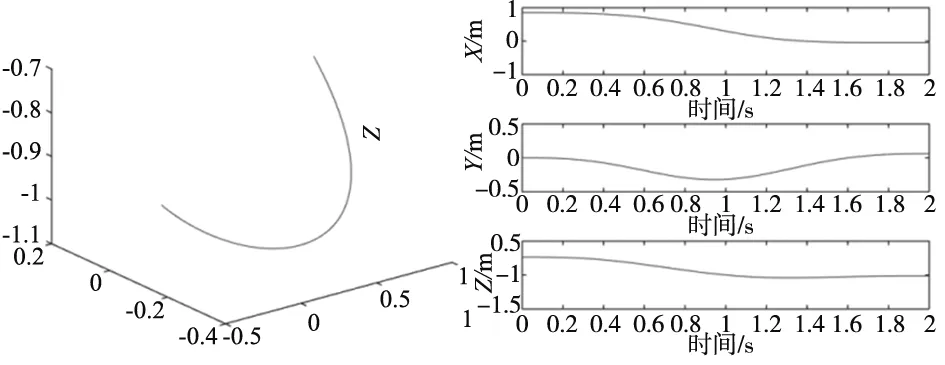
图2 机械臂末端执行器运行轨迹
1.3 目标函数
机械臂末端执行器在满足运动学约束、动力学约束和负载约束件下,以工作时间最优化为目标,其目标函数与约束条件束设计如下:
(4)
式中,tij为第i个关节运行轨迹的第1、2、3段的运行时间;h(t)为第i个关节完成运行轨迹总时间;j=1,2,3。
(1)运动学约束

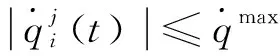
(2)动力学约束
假定机械臂未发生碰撞,则τf=0
负载约束:Fgmin≤Fk≤Fgmaxk=1,2
式中,Fk为末端执行器夹持力;Fgmin为最小夹持力;Fgmax为最大夹持力;
2 算法原理及步骤
2.1 原始算法
在算法优化时,引入量子位和量子叠加这两个概念后,构造出量子遗传算法。量子位为量子计算表达式中最小的信息计算单位。一个量子位具有三种状态表示方式,如式(5)所示[6]。
|φ>=α|0>+β|1>
(5)
式中:α,β表示相应状态出现概率幅值的2个复数。

每个长度为m个量子位的q染色体表示如下:
(6)

(7)
(8)
(9)
由此一个完整的染色体可以表示为:
Xq=[UqTqNq]
(10)
2.2 自适应动态旋转角步长调整机制
量子旋转门旋转角θi,其大小和方向取决于选定的调整策略,θi过大,则染色体更新幅度增加,易导致未出现全局寻优即收敛。θi过小,则染色体更新幅度减小,易导致局部寻优[7-8]。
文中引入自适应动态旋转角步长调整机制,算法优化设计时,面对多样化的适应度值,能够及时调整个体进化所需的旋转角Δθ,确保及时跳出局部最优,并在全局阶段具有良好的寻优性能。旋转角查找表如表2所示。
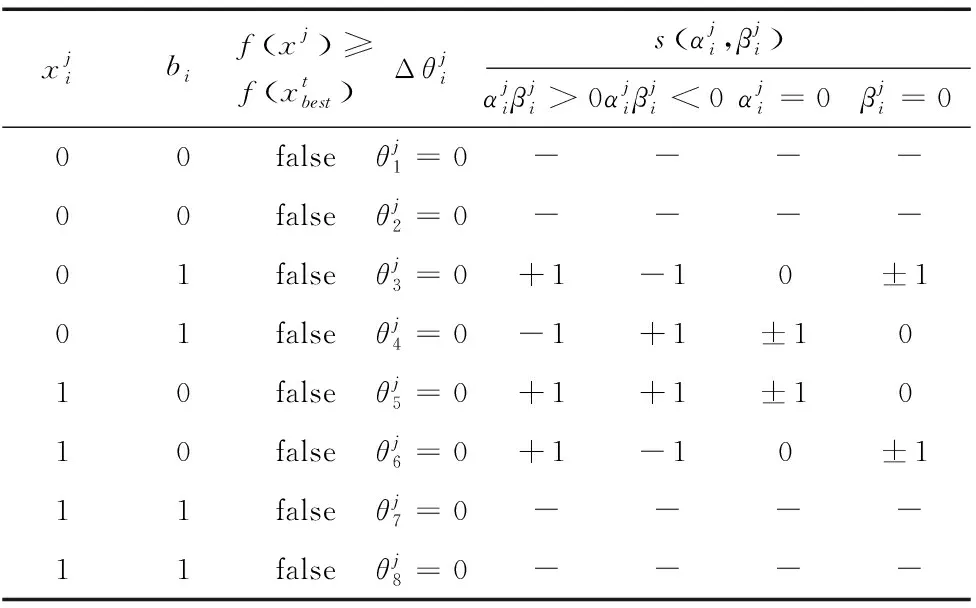
表2 自适应量子遗传算法旋转角步长查找表
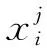

(11)
当前种群中,第j个个体的第i位的进化旋转角步长和旋转方向可由式(12)计算:
(12)
2.3 多算子协同变异机制
算法优化设计时,合理参考多个评价算子的求解结果,协同确定迭代计算时的变异概率,利于提高后期优化时种群多样性和搜索全局最优解的稳定性。因此,文中引入多算子协同变异机制,即设定个体相似度评价算子、个体适应度评价算子和种群变异调整算子。
个体相似度评价算子xsim用以评价当前种群内个体差异情况,其定义如式(13)所示:

(13)
式中,dmax和dmin分别表示当前种群中与最优个体之间汉明距离最大和最小的个体,davg表示当前种群所有个体与最优个体之间汉明距离的均值。
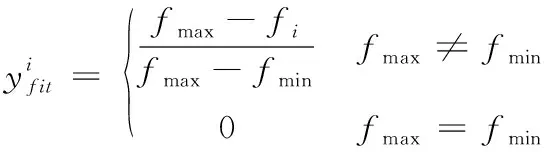
(14)
式中,fmax和fmin分别表示当前种群中最优适应度值和最差适应度值,fi表示当前种群中第i个个体的适应度值。
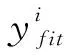
种群变异调整算子Facc(n)如式(15)所示,为当前进化代数n的表达式,算子逐步提升个体变异概率,推动算法优化设计时能够跳出局部最优解,避免陷入早熟。
Facc(n)=
(15)
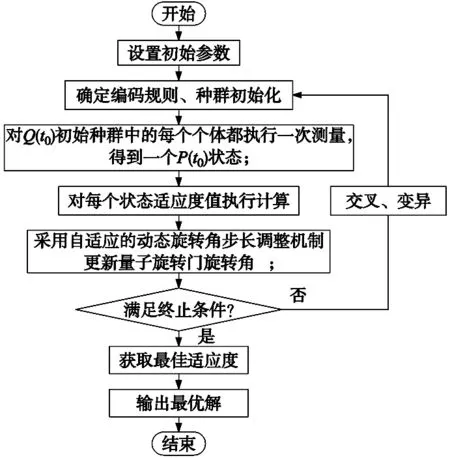
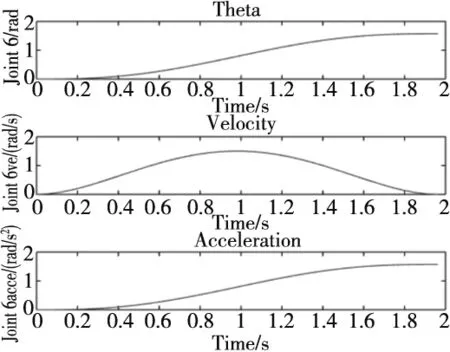
式中,n表示当前进化代数,s表示算法定义的最大进化代数,常数T表示算法迭代过程中,种群最优解连续不发生变化的迭代次数,C(0 当种群中的最优适应度值连续T代未发生变化并且未达到最大进化代数s的时候,则在T+1代的时候,Facc(n)会在第T代的基础上增加一个变异概率值,增加的值由s、n和C确定。 此外,在算法的执行过程中可以通过设定阀值使Facc(n)趋于固定值。 改进量子遗传算法流程如图3所示,具体步骤如下: (2)对Q(t0)初始种群中的每个个体都执行一次测量,得到一个P(t0)状态; (3)求解计算不同状态下的函数适应度值; (4)依据自适应的动态旋转角步长调整机制更新量子旋转门旋转角θi; (5)判断是否满足结束条件,若满足,则进入步骤(6),否则,迭代次数t=t+1继续步骤(8); (6)记录最优个体,输出最佳适应度值; (7)输出最优解,算法流程结束; (8)在量子交叉中,以轮盘赌方式拣选个体。 图3 改进量子遗传算法流程图 选取三种具有不同特征的典型基准测试函数进行分析,验证改进量子遗传算法的优化性能[9-10]。 (1)Sphere model函数: (16) 式中,-100≤xi≤100;min(f)=f(0,0,…,0)=0。 图4 Sphere model函数图像 (2)Generalized rosenbrock函数 (17) 式中,-30≤xi≤30;min(f)=f(1,1,…,1)=0。 图5 Generalized rosenbrock函数图像 (3)Geneealized rastrigin函数 (18) 式中,-5.12≤xi≤5.12;min(f)=f(0,0,…,0)=0。 图6 Geneealized rastrigin函数图像 合理设置初始参数,依据上述基准测试函数进行仿真测试,结果如图7~图9所示。 图7 Sphere model函数收敛曲线 图8 Generalized rosenbrock函数收敛曲线 图9 Geneealized rastrigin函数收敛曲线 图7~图9为基准测试函数在在不同优化算法下的收敛曲线,对比可知,改进量子遗传算法使得基准测试函数更加迅速趋于收敛,计算结果稳定效率更高。结果表明量子遗传算法引入多算子协同变异机制和自适应动态旋转角步长调整机制后,提高了全局搜索能力,能够在较短时间内跳出局部最优。获取最优解所需进化代数较少,缩短收敛周期,优化求解结果提升解的质量,具有较强的实用性。 文中以串联机械臂为验证对象,设置改进量子遗传算法初始参数后,对机械臂运行轨迹进行优化设计,算法优化时函数适应度曲线如图10所示,所得机械臂各关节角位移、角速度、角加速度变化曲线如图11所示。 图10 函数适应度曲线 (a) 关节1变化曲线(b) 关节2变化曲线 (c) 关节4变化曲线(d) 关节5变化曲线 (e) 关节6变化曲线 由上图可知,在满足各约束条件的前提下,通过改进量子遗传算法以轨迹运行时间为目标,将初始运行时间2 s优化为1.956 s,且优化后各关节角位移、角速度和角加速度变化曲线平滑、稳定、连续,无突变现象产生。通过改进量子遗传算法有效缩短机械臂末端执行器轨迹运行时间的同时,保证运动过程没有很大的振动,实现了机械臂的平稳运行。 本文以六自由度机械臂仿真模型为例,借助MATLAB工具结合五次多项式样条插值函数,构造机械臂末端执行器轨迹运行三维图。提出一种改进量子遗传算法,以轨迹运行时间为目标进行优化设计,将运行时间2 s优化为1.956 s,最终得到结论如下: (1)文中面向优化过程中不同个体的适应度值,选用自适应动态旋转角步长调整机制,实时更新子旋转门旋转角θi,保障全局设计时具有良好的搜索性能。 (2)文中设定多个评价算子协同确定种群中不同个体的变异概率,增加了算法进化后期的种群多样性,提高算法搜索全局最优解的稳定性。 (3)文中以轨迹运行时间为目标进行优化设计,将运行时间2 s优化为1.956 s,验证算法优化性能同时,提高串联机械臂的整体工作效率,为后续研究与分析奠定理论基础。2.4 改进量子遗传算法流程
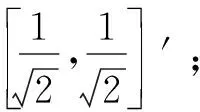
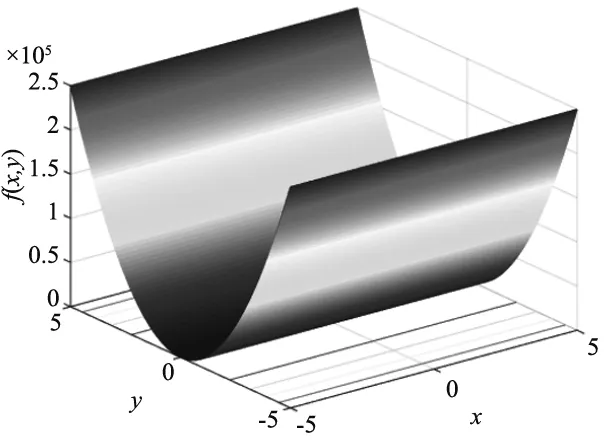
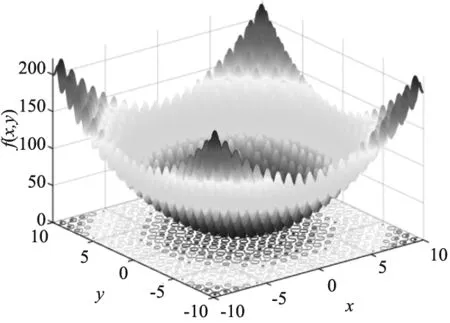
3 函数验证


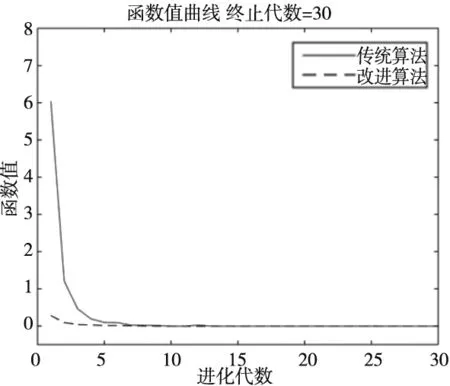
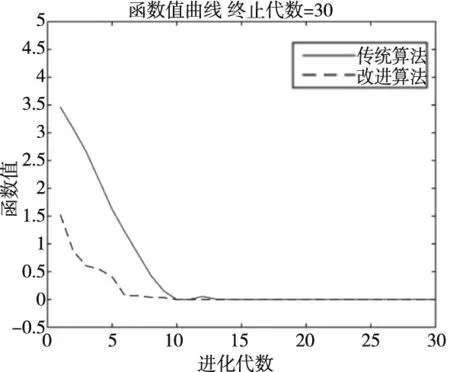
4 优化结果
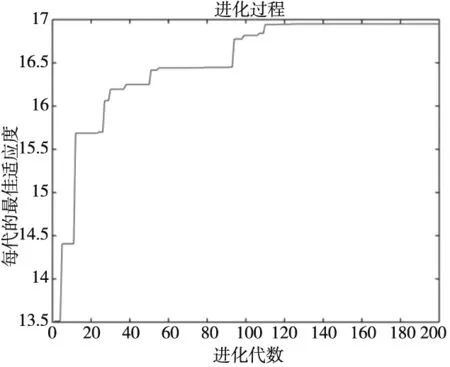

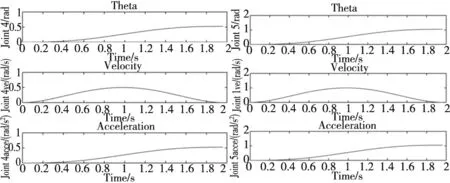
5 结论
