考虑工人分配的多目标装配线平衡优化*

邓 超，胡瑞飞，蒋捷峰，殷国富

(四川大学机械工程学院，成都 610065)

0 引言

装配线平衡问题(Assembly Line Balancing Problem, ALBP)主要是研究在满足各类约束的条件下，如何将各装配工序合理分配入工位，达到减少人力和设备资源浪费、降低成本和提高装配效率等目的。

近年来，学者们对于装配线的研究主要集中于改进数学模型和算法，使数学模型能有效反应实际情况，算法求解效率和精度更高。如李爱平等[1]提出了装配复杂性的测度方法，并建立了考虑装配复杂性的ALBP数学模型，应用改进的遗传算法求解变速箱实例，结果表明了方法的有效性。王共冬等[2]定义了能力因子，用于修正工人和设备对装配线的影响，采用改进后的Memetic算法求解，通过对比说明了该方法求解结果更符合实际。徐立云等[3]建立了考虑作业人员疲劳的多目标优化数学模型，利用改进的粒子群优化算法求解轴承座分装线，验证了方法的有效性。Pereira J等[4]为了解决以成本为导向，考虑任务分配和设备决策的机器人ALBP，提出了一种结合遗传算法和其他优化方法的混合式算法，通过实验证明了算法的优越性。刘雪梅等[5]考虑工位复杂度对装配线的影响，提出工位复杂性测度方法，建立ALBP模型，以某变速箱装配线为例，采用改进的遗传算法有效求解了该问题。

目前很多装配线依然以人工为主，工人作为装配线中最具能动性的因素，应充分考虑其带来的影响[6]。大部分学者从人机工程学角度出发，如曹婧华[7]提出考虑工人心理承受和疲劳恢复的ALBP模型，应用遗传算法求解，求解结果更具使用价值。Bortolini M等[8]提出了最小化节拍和人机工程学风险的多目标ALBP模型，以某厨房电器装配线为例验证了多目标模型。Battini D等[9]提出装配线平衡和零件供给的综合问题，考虑人机工程学，建立了整数混合模型。少部分学者研究了ALBP中的工人分配问题，如Sungur B等[10]将工人技能等级排序，根据任务技能需求不同进行工人合理分配，建立总成本最小为优化目标的数学模型。Oksuz M K等[11]根据不同工人对不同任务的绩效不同，从作业绩效均衡性角度，建立了装配线工人分配和平衡问题的非线性模型，使用人工蜂群算法和遗传算法求解该类问题。上述从工人角度出发的ALBP研究，以工人会所有工序操作为前提，未考虑工人技能水平不一，工序难度等带来的影响。实际中，工序重新分配后，工人上岗可能会需要学习部分工序操作，给企业带来培训成本，且学习的时候，装配线不能正常运行，会给企业造成重大损失。因此需要对工人进行合理分配，使得全部工人需要学习的总时间尽可能最少。

目前文献缺乏对这一角度的工人分配方法和数学模型研究，本文为此提出了一种基于匈牙利算法的工人分配方法，建立了考虑工人分配的多目标优化模型。并针对此模型，设计了多目标鲸鱼优化算法，最后应用于某公司连接器实例。

1 装配线优化模型构建

1.1 工人分配

装配线工人指派问题可描述为：已知n个工位中的工序内容、m个工人及其会操作的工序情况和工人学习各工序操作所需的平均时间sti(i=1,2,…,n)，按照一个工位只需要一个工人，一个工人不能被重复分配的原则，合理从m个工人中分配n个工人至n个工位，使工人学习总时间最少。

工人学习时间情况矩阵WSn×m，行代表工位，列代表工人，WS(i,j)=k，代表工人j去工位i需要学习k分钟。根据工人分配原则，问题转化为从矩阵WS中的不同行不同列选取n个数，使其总和最小。本文采用匈牙利指派算法求解此问题，该算法基于如下性质：

设指派模型的效益矩阵为Ci,j(本文为WS)，若Ci,j某行或列减去同一个常数，得到新矩阵Bi,j,以Bi,j或Ci,j为效益矩阵的指派模型具有相同的最优解(相同的指派方式)[12]。

算法步骤如下：

步骤1：用0元素补全矩阵WSn×m为方阵WSm×m；行归约：每行所有元素减去该行元素最小值；列归约：每列元素减去该列元素最小值。

步骤2：用最少的直线覆盖方阵中的0，若直线数小于方阵维度m，则转至步骤3，若等于则转至步骤4。

步骤3：找出未被直线覆盖的数中的最小值min，未被画线的行减去min，画线的列加上min，移除直线，转至步骤2。

步骤4：移除补全方阵时的0元素，找出n个不同行不同列的0元素，被选择的0元素代表最终分配方案。

1.2 考虑工人分配的装配线多目标优化模型

(1)模型将会涉及的符号说明如表1所示。

表1 符号说明表

(2)确定目标函数：

(1)

(2)

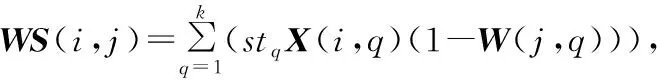
(3)

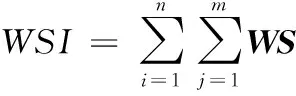
(4)

minf=[CT(x),SI(x),WSI(y,z)],
(x∈X,y∈WS,z∈WA)

(5)

式(1)为生产节拍计算方法；式(2)为平滑指数计算方法；式(3)表示WS中元素的计算方法；式(4)为工人学习总时间计算方法；式(5)表示优化目标为生产节拍CT、平滑指数SI和工人学习总时间WSI，综合考虑了生产效率、装配线平衡和工人技能情况，其中x，y，z为决策变量。

(3)约束条件：

(6)

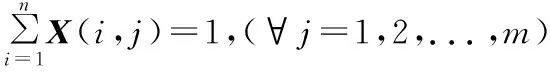
(7)

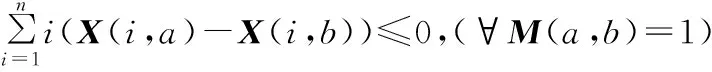
(8)

(9)

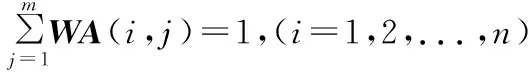
(10)

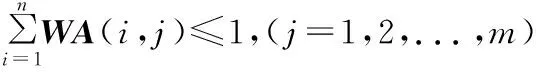
(11)

式(6)～式(8)为工序分配约束，表示每一个工序都被分配入了工位中、未被重复分配和满足优先关系；式(9)为工位作业时间约束，表示各工位作业时间应不大于节拍；式(10)和式(11)为工人分配约束，表示各个工位需要一个工人，且工人未被重复分配。

2 多目标鲸鱼优化算法(MOWOA)

2.1 鲸鱼优化算法(WOA)

Mirjalili S等[13]在2016年提出了WOA。该算法具有参数少，原理简单，求解精度高等优点[14]。WOA实质是模拟鲸鱼捕食行为，鲸鱼更新位置方式有3种：包围捕食、泡网攻击和随机搜寻猎物。

(1)包围捕食

此方式是模拟鲸鱼找到并包围猎物的捕食行为，在WOA中，假定最优候选解是猎物(头鲸)所在位置，其他鲸鱼将靠向头鲸进而更新自己的位置。位置更新的数学表达式为：

D=|C·X*(t)-X(t)|

(12)

X(t+1)=X*(t)-A·D

(13)

式(12)和式(13)中，X*(t)代表第t代头鲸的位置，X(t)代表第t代中鲸鱼个体的位置，t为迭代次数，A和C为系数变量A和C定义如下：

a=2-(2t/M)

(14)

A=2a·r1-a

(15)

C=2·r2

(16)

式(14)为收敛因子a更新公式，其中M为最大迭代次数，表示a随着迭代从2线性递减到0。式(15)和式(16)为A，C更新公式，其中r1和r2为[0,1]之间的随机数。

(2)泡网攻击

此方式是模拟鲸鱼气泡捕食行为，分为两种策略，描述如下：

1)摇摆包围捕食

此阶段鲸鱼位置根据式(13)更新，此过程A取值范围为[-a,a]，若A在[-1,1]之间，鲸鱼将会更新到当前位置和头鲸位置之间。

2)螺旋式气泡捕食

此阶段，鲸鱼计算出自身到头鲸的距离，接着螺旋式移动靠近头鲸，数学模型如下：

D′=|X*(t)-X(t)|

(17)

X′(t+1)=D′·ebl·cos(2πl)+X*(t)

(18)

式(17)和式(18)中D′为第i头鲸鱼到头鲸的距离，b为螺旋形状常数，l为[-1,1]之间的随机值。

假定鲸鱼执行两种捕食策略的概率各为50%，则此阶段鲸鱼位置更新公式为：

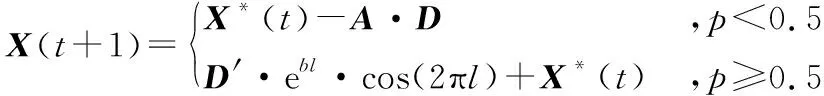
(19)

式中，p为[0,1]之间的随机数。

(3)随机搜寻猎物

此方式是模拟鲸鱼随着伙伴随机搜寻猎物的捕食行为。鲸鱼更新位置是以A值为基础，当|A|>1时，鲸鱼不再跟着头鲸更新位置，而是全局随机搜寻猎物，跳出局部最优。位置更新公式如下：

D=|C·Xrand-X(t)|

(20)

X(t+1)=XrandT-A·D

(21)

式(20)和式(21)中，Xrand为当前鲸鱼种群中一个随机个体所在的位置。

2.2 鲸鱼位置的编码与解码

本文采用基于权重的鲸鱼位置编码解码方式，得到工位信息矩阵X，为后续计算决策变量值提供数据支持。

鲸鱼个体位置由N(工序总数)个随机数排列组成，编码时，随机数的索引值代表工序，数值大小代表对应工序的权重，权重大的工序会优先得到分配。

在上述编码方式下，解码分为3个步骤：

步骤1：生成工序顺序集合R，该集合满足工序优先顺序，并符合权重优先规则。

步骤2：将集合中的工序分配入各个工位中，得到工位信息矩阵X。

步骤3：求出各工位作业时间、工人学习时间和工人分配方案。

2.3 多目标鲸鱼优化算法设计

(1)外部备选解集paretoSet更新机制

paretoSet中解的个数确定为n。合并上一代paretoSet和当前鲸鱼种群为待选解集allSet。对allSet进行层级划分、拥挤度排序和删除部分重复解等操作，从中选取n个备选解，更新paretoSet。

层级划分方法：从allSet中选出非支配鲸鱼个体，加入nonbadSet集合，剩余鲸鱼个体加入badSet集合。其中非支配鲸鱼个体代表其目标函数值不全劣于其他个体。

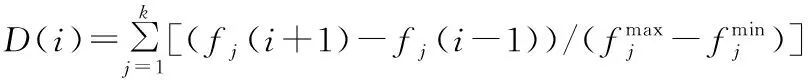
(22)

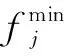
具体更新算法伪代码如下：

图1 pareto解集更新算法流程图

算法在paretoSet最后一次执行解添加操作时，对当前层的非劣解集进行拥挤度排序和删除重复解操作，适当增加解的多样性的同时，保证解的优越性。

(2)头鲸选择方式

合并当前种群和paretoSet为allSet，从中选出头鲸备选个体，并加入集合selectSet，从selectSet中随机选取一个鲸鱼个体作为头鲸，使算法较均衡地往各个目标函数值最优方向搜索，提高解的优越性。头鲸选择算法伪代码如下：

图2 头鲸选择算法流程图

(3)多目标鲸鱼优化算法

综上所述，MOWOA伪代码如下:

图3 MOWOA算法流程图

3 应用实例

3.1 连接器实例介绍

本文实例来源为某公司连接器，如图4所示，其内部结构复杂。经过现场实地调研，收集和整理相关数据，得到连接器装配线工序信息、工人技能情况和工序学习时间等数据。工序作业时间如表2所示，装配工序顺序如图5所示，工人已会工序情况如表3所示，工序学习时间如表4所示。

图4 连接器产品图

表2 工序作业时间

续表

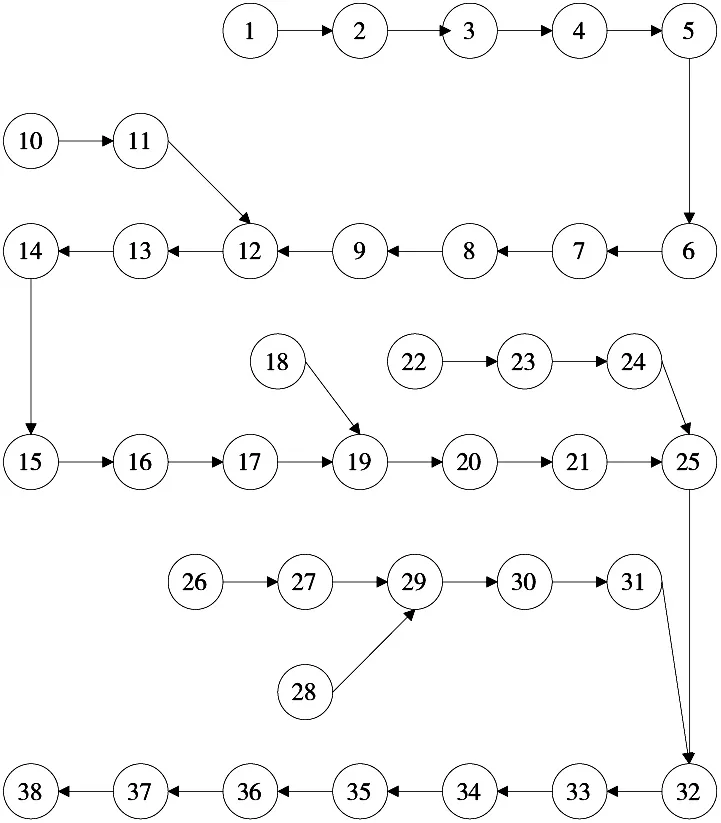
图5 装配顺序图

表3 工人技能情况表

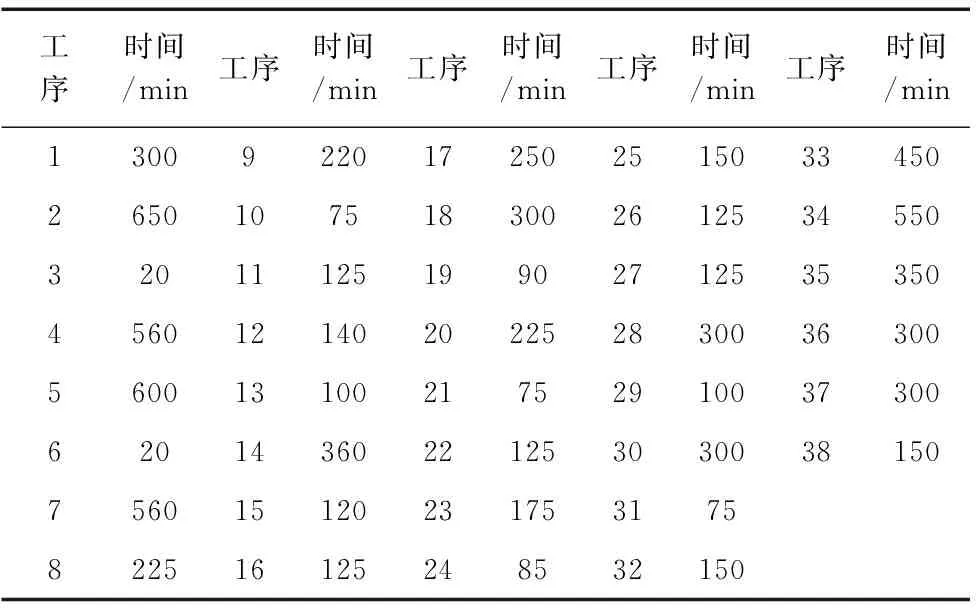
表4 工序学习时间表

3.2 结果分析

本文装配线实例给定工标题系位数为12，根据前文建立的数学模型，在Windows10 64位操作系统、内存8G处理器Intel(R)Core(TM)i5-8400的计算机配置下，采用MATLAB编程，算法参数设置如表5所示。

表5 算法参数表

图6～图8为节拍、平滑指数和工人学习时间3个目标的优化过程，表示每代鲸鱼种群中各目标的最优值。由图可知，3个目标经过多次迭代后都到达一个较低的值收敛，证明了算法能有效优化3个目标。

图6 CT优化过程图

图7 SI优化过程图

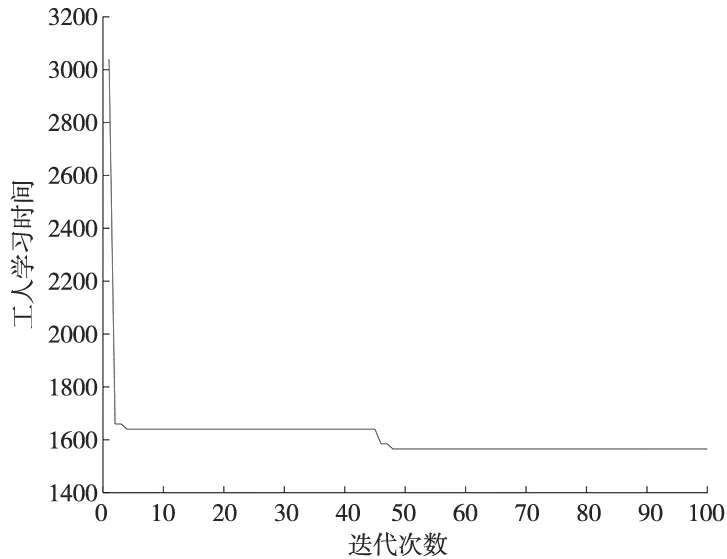
图8 工人学习时间优化过程图

图9 由最后的pareto解集得来，以工人学习时间优化目标为x轴，节拍和平滑指数为y轴。由图9可知，整体上节拍和平滑指数与工人学习时间呈负相关，说明CT/SI更优的工序分配下，工人分配后，工人学习时间更多，三者难以同时保证最优，决策者可根据倾向从pareto解集中选择相应解。

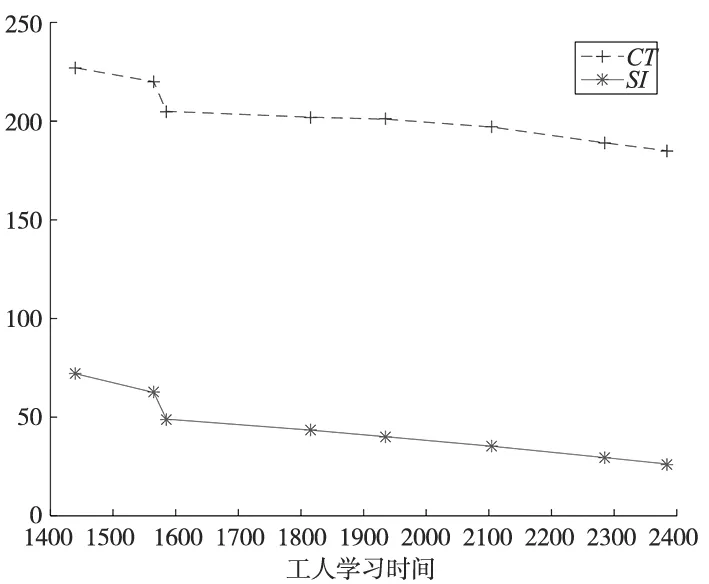
图9 优化目标关系图

从最后解中选择了4种具有代表性的分配方案，如表7～表9所示，符号说明见表6。

表6 符号说明表

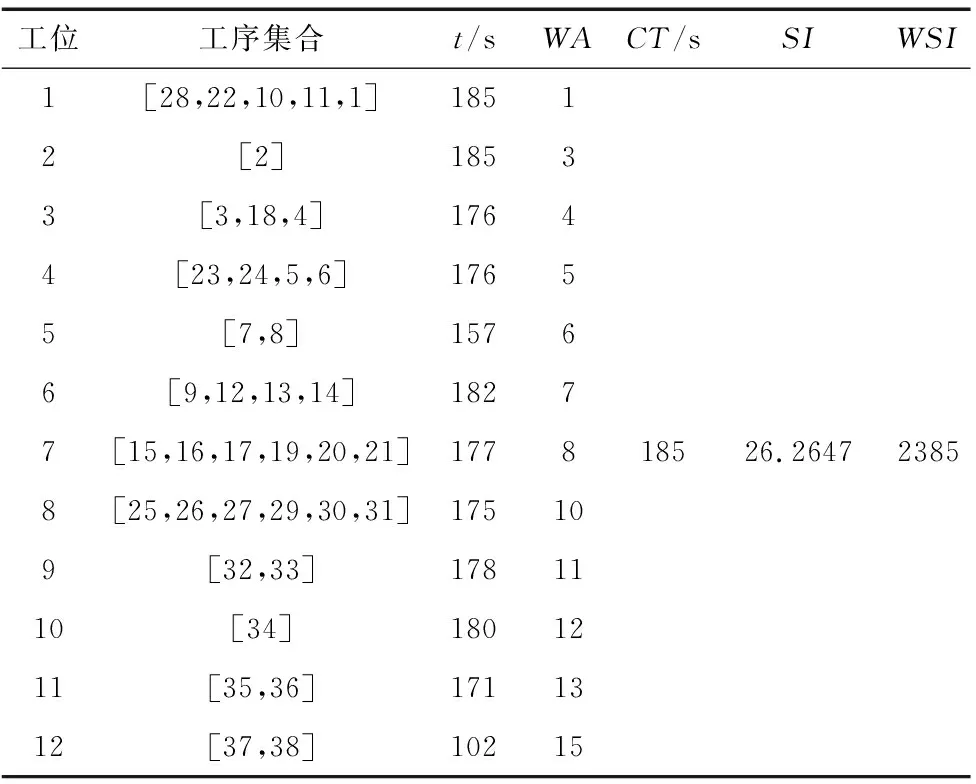
表7 工序分配方案1

表8 工序分配方案2

表9 工序分配方案3

由表7～表9可知，工序分配符合装配顺序，未出现重复分配和少分配的情况；工人安排也符合分配原则，说明算法求解结果符合模型所定约束。由表8可知，不同的工序和工人分配，优化目标值可能相同。这使得企业决定方案时灵活性更大。

4 结束语

本文分析了目前ALBP中对工人研究的不足，为提高装配效率和降低成本，提出了工人分配方法、多目标优化模型和多目标鲸鱼优化算法。以匈牙利算法进行工人分配的方式，能使工人学习时间最少，从而降低工人学习带来的影响。以某公司连接器为例，验证所提模型与算法，发现算法求解结果符合模型所定约束，且优化效果明显，说明算法能有效解决该类模型问题；生产节拍和平滑指数降低时，工人学习时间呈上升趋势，优化目标间呈明显博弈；同一优化结果下，工序和工人分配方案可能不同。本文方法能提供多组优秀解，企业决策者可根据实际情况选择分配方案。接下来将继续探索符合实际的优化目标，设计更具效率的优化算法。