基于深度学习的冗余机械臂无碰运动规划*
2021-07-02季晓明文怀海
季晓明,文怀海
(1.江苏安全技术职业学院电气工程系,江苏 徐州 221011;2.大连理工大学机械工程学院,辽宁 大连 116024)
0 引言
工业机器人是智能制造领域的重要构成单元,被广泛应用于3C行业、汽车制造、食品包装及航空航天等领域,在国民经济与社会发展中起着重要作用。在机器人技术中,冗余机械臂无碰运动规划问题一直是国内外的研究热点[1-2]。该问题研究的是在避免碰触到周围环节障碍物的前提下,寻找从初始位形到目标位形的机械臂运动,其中避碰是核心。
机械臂的避碰研究一般分为全局避碰法与局部避碰法两种[3]。前者需预先获得机械臂周围环境信息,再对机械臂进行离线规划,常见的方法有A*搜索[4]、马尔科夫决策法[5]、随机树形搜索法[6]等。这些方法虽能有效解决机械臂的避碰运动规划,但也会带来诸如关节位姿无法约束、算法极易陷入局部最优值、实时性较差等问题,故不易得到推广。局部避碰法中含有碰撞检测环节,可根据机械臂运动状态与障碍物信息实时作出避碰决策,这也是目前最受学者青睐的方法。例如,曹博等采用改进人工势场法分别在任务空间和关节空间内建立势场引导7自由度机械臂的无碰运动,该算法的可行性在仿真和试验下得到了验证[7]。Shen H Y等采用主从任务转化法实现了避碰运动与机械臂末端执行器运动的主从优先级转化,降低了计算量和减少了运动奇异性出现的概率[8]。Chen Y J等用椭球模型近似描述障碍物与机械臂连杆,提出了基于虚拟力的避碰运动规划方法[9]。然而,上述方法大都将障碍物简化成一个质点或球形,忽略了机械臂连杆与障碍物原有的三维几何信息,这样会导致关节速度激变、末端执行器运动精度变差。
本文提出了一种基于深度学习的冗余机械臂避碰运动规划方法,该方法的核心算法是基于天牛须搜索机制的循环神经网络算法(Beetle Antennae Olfactory Recurrent Neural Network,简称BAORNN),这属于位置级而非速度级的运动规划,即规划过程中不要求末端执行器的初始位置处于参考轨迹上,可避免雅可比矩阵的计算、提高计算效率。另外,本算法中碰撞检测策略选择的是Gilbert Johnson Keerthi (简称GJK)算法,它能有效描述两个多面体之间的距离[10]。最后,通过仿真算例对本文所提算法的可行性和有效性进行了验证。
1 问题描述
考虑冗余机械臂跟踪一条光滑曲线,其实质是将关节空间的运动轨迹投影到任务空间末端执行器的运动轨迹中,即可通过正向运动学来实现上述功能[11]:
x(t)=f(θ(t))
(1)
式中,t为时间,x(t)∈Rn为末端执行器位形,θ(t)∈Rm为关节角序列,m>n代表了机械臂构型上冗余。基于式(1),可获得冗余机械臂逆向运动学的描述形式为:
θ(t)=f-1(x(t))
(2)
在机械臂实际操作中应预先规划好末端执行器的运动轨迹xr(t)。为了跟踪该轨迹,关节角序列必须满足[12]:
θ(t)=f-1(xr(t))
(3)
根据冗余机械臂的结构特性可知,式(3)存在关节角的多组解,即存在冗余性。为解决上述问题,需从关节空间中找出一组合适解,进而可将轨迹规划问题转化成如下函数优化问题:
(4)
这里的gtr(·)是轨迹规划目标函数,其具体形式为:
(5)
在轨迹规划问题中考虑避碰条件以保证冗余机械臂安全作业。选择最大化末端执行器与障碍物之间的最小距离作为避障目标函数,并将其添加到式(4)中,有:
(6)
式中,O是障碍物顶点的笛卡尔坐标,gOI(·)是避障函数,即:
(7)
式中,β是超参数,di(O,θ(t))是第i根连杆到障碍物顶点的距离,由GJK算法计算获得,具体形式如下所示:
(8)
式中,VA∈RnA×3和VB∈RnB×3分别为三维空间中不规则体A与B的顶点集合,nA和nB是最大顶点数。
由式(8)可知,GJK算法需要连杆和障碍物的几何信息。定义连杆顶点函数为Mi(θ)∈Rni×3,即:
Mi(θ)=Ri(θ)Mi(0)+Ti(θ)
(9)
式中,ni是第i根连杆的顶点数,Ri(θ)和Ti(θ)分别为第i根连杆的转动矩阵和移动矩阵。
2 BAORNN算法
冗余机械臂的避障控制包含三部分:轨迹规划、避碰及关节角约束。综合这些要求并将其转换成函数优化问题,即:

(10)
式中,g(·)是总优化目标函数,其具体形式为:
g(O,xr(t),θ(t))=ω1gtr(xr(t),θ(t))+ω2gOI(O,θ(t))
(11)
式中,ω1和ω2为权重因子。
本文用BAORNN算法来求解上述优化问题。其中,BAO算法模拟的是天牛在未知环境下搜寻食物的过程,即天牛根据两个触须获得的气味大小来确定下一步的走向[13]。在这个过程中,天牛不会在任何方向上随机移动,而是用嗅觉判明方向后,再做出下一步的计算决策,这可保证算法的多样性。算法的数学机理为:
假设在第k次迭代时,机械臂的关节位置为θk,用标准正态分布函数b∈Rm模拟天牛左右两个触须接收到的气味信息,即:

(12)
式中,λk是模拟两触须间距离的超参数,θkL和θkR分别为第k次迭代时左右关节角(对应两个触须气味信息),该位置应满足如下约束:
ΩθkX=PΩ(θkX)
(13)
式中,X∈{L,R}。PΩ是关于集合Ω的投影函数,其数学描述为:
(14)
集合Ω的数学描述为:
Ω={θ∈Rm|θ-<θ(t)<θ+,di>dmin}
(15)
式中,di=di(O,θ(t))。
结合式(10)与式(13),可得到用来评价当前关节位置的目标函数:
gkX=g(O,xr(t),ΩθkX)
(16)
进而,设计第k+1次迭代时关节预测位置为:
Ωθk + 1=PΩ[θk-δk(λk)sign(gkL-gkR)b]
(17)
式中,sign(gkL-gkR)b为符号函数,能保证天牛向着目标函数较小的触角方向移动。δk(λk)为超参数,用来计算θ(k+1)X与θkX间的欧氏距离。上式可在预测的左右关节角中抉择出较优值。
第k+1次迭代时预测关节角对应的目标函数为:
(18)
更新冗余机械臂的关节角与目标函数,即:
(19)
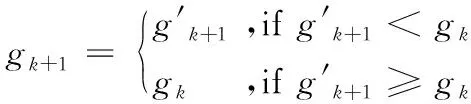
(20)
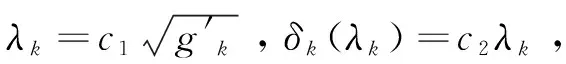
进而,将BAO算法添加进RNN中形成BAORNN算法,去解决冗余机械臂的避碰运动规划问题,算法的流程如图1所示。
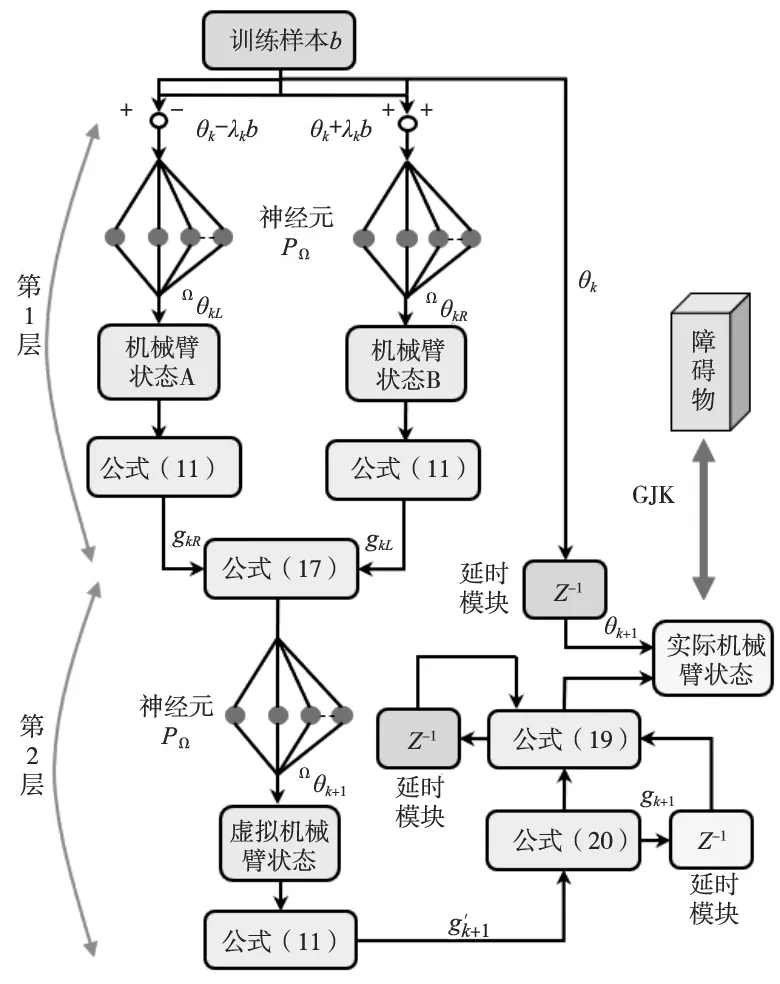
图1 BAORNN算法流程图
其中,RNN是一种常见的深度学习策略,其包括输入层、隐藏层和输出层,它将冗余机械臂关节角预测问题转换为前后有依赖性的两层时间序列问题,整个结构包括3m+6个神经元。在每个隐藏层中,用投影函数PΩ作为每个神经元的激活函数,并通过目标函数g(·)来判断信号流向。根据上述分析可知BAORNN算法的计算复杂度为O(m),即计算复杂度为关节数的线性函数,故可在普通计算机上高效率运算。
3 仿真算例
为验证本文所提避障算法的合理性,选取文献[14]提出的7-DOF冗余机械臂作为分析对象,该机械臂类似于肩腕关节偏置的仿人手臂,具有灵活性高、柔顺性好的特点,如图2所示。相应的DH参数也在表1中给出。另外,BOARNN算法的参数设置为:c1=0.6,c2=0.7,Tmax=500,ω1=0.7,ω2=0.3。仿真环境为Inter Core i7-4720 PC,MATALAB 2020a。
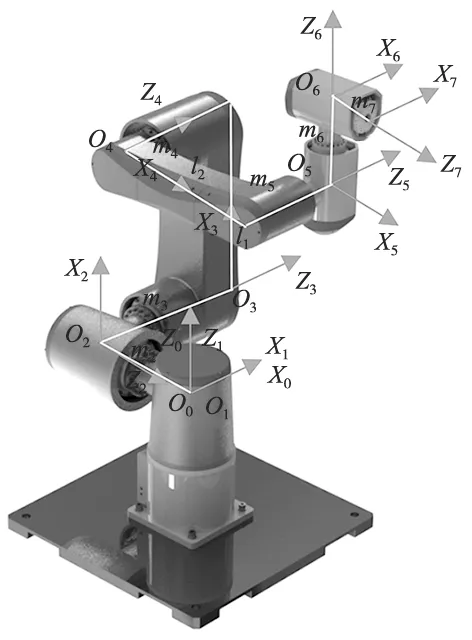
图2 7-DOF冗余机械臂

表1 冗余机械臂的DH参数
仿真中,利用蒙特卡罗法[15]按照标准正态形式随机生成机械臂的可达工作位形,并作为训练样本来训练网络。蒙特卡罗法的计算公式为:
θi=θimin+(θimax-θimin)·randn(0,1)
(21)
式中,randn(·)为呈正态分布的随机函数。将生成的随机关节角代入到正向运动学公式(1),便可获得冗余机械臂末端执行器的位形。这里的训练样本由1000个位形构成(如图3所示),取其中700作为训练集,300作为测试集。

图3 冗余机械臂的随机位形
为了评价预测结果的优劣,选取单次预测的精度评估公式为:
(22)
式中,Ωθ是预测关节角,θ是参考关节角,δ为预测精度。对双隐藏层的BAORNN算法,分别选取神经元数为15、21、27、33和39进行训练,其预测精度如图4所示。从图中可以看出,随着隐藏层神经元数目的增加,BAORNN算法的预测精度也随之增加,当数目逾27后,预测精度却开始下降,故选择隐藏层的神经元数目为27。
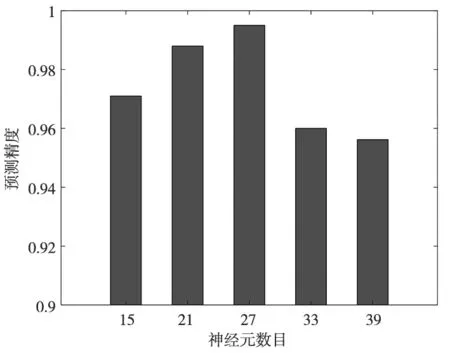
图4 预测精度
用训练好的网络预测测试集中的末端执行器位形,并计算其相对误差,结果在图5中给出。从图中可以看出,在BAORNN算法的帮助下,测试集的相对预测误差均小于5%,这说明了本文所提算法预测准确性较高。
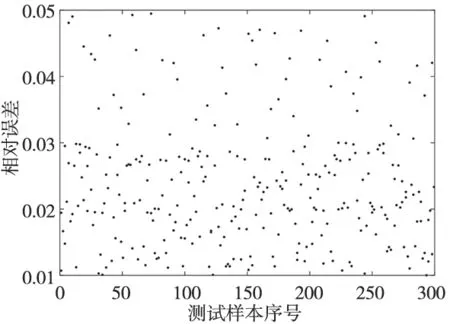
图5 BAORNN相对预测误差
接着选取四面体的一个面作为待加工面,机械臂的末端执行器需沿着其三个顶点运动,此过程可模拟机器人焊接、喷涂等过程。假设工作环境中有一长方体障碍物,要求机械臂绕开障碍物并依次达到三个目标点位置。表2给出了待加工面和障碍物的坐标信息。为了比较BAORNN算法的性能,引入改进人工势场法[7]进行比较,结果如表3所示。

表2 待加工面与障碍物的信息
从表3中可以看出,BAORNN算法的预测精度比改进人工势场法平均高出10.89%、算法时间节约2.44 s。同时,基于BAORNN算法的冗余机械臂的无碰运动规划效果如图6所示。从图中可以明显看出机械臂的避碰过程和运动过程。图7给出了7个关节角的响应,过程中没有出现严重的关节突变,变化过程较为平滑、柔顺。上述结果验证了本文所提算法的可行性与优越性。

表3 两种算法预测能力的对比
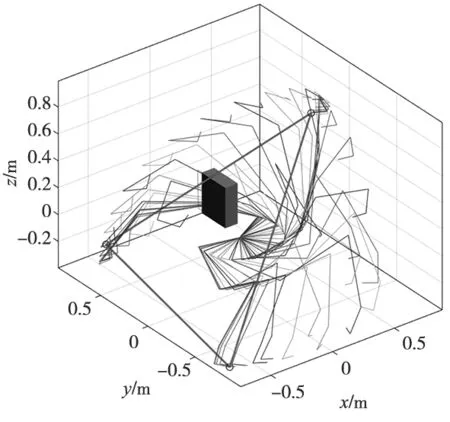
(a) 三维轨迹图
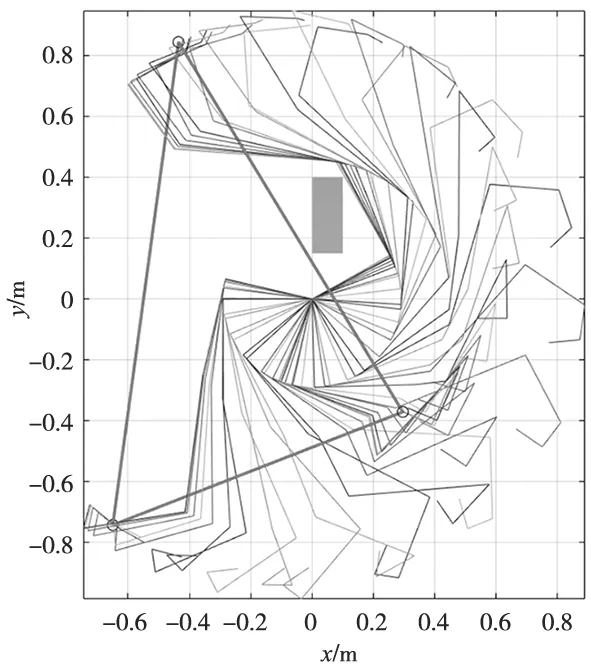
(b) XY平面内的轨迹 图6 冗余机械臂的运动规划结果

图7 关节角的响应
4 结束语
本文针对冗余机械臂无碰运动规划问题,提出使用BAORNN算法进行预测,主要结论如下:
(1)BAORNN算法的预测精度与神经元数目有关,仿真中最佳神经元数目为27,此时算法的预测精度最高。
(2)BAORNN算法的相对预测误差小于5%,基本上能满足本文冗余机械臂无碰运动规划的需求。
(3)与改进人工势场法相比,BAORNN算法的平均预测精度要高出10.89%,运算时间节约2.44 s。
(4)BAORNN算法具有较高的预测精度,能够较好地解决冗余机械臂避碰运动规划问题。
