基于改进遗传算法的机翼装配序列智能规划*

郝 博，徐东平，王明阳，王建新

(1.东北大学机械工程与自动化学院，沈阳 110819； 2.东北大学秦皇岛分校控制工程学院，河北 秦皇岛 066004)

0 引言

在世界经济飞速发展和竞争日益激烈的今天，制造业迎来了巨大的挑战。对于制造业企业而言，产品从设计、加工到装配过程，其效率和成本是今后发展的重点，也是提高竞争力的关键。研究表明，产品的装配过程占总体生产工作所需时间的20%～70%[1]。同时，装配过程消耗了总体制造成本的大部分，适当的装配顺序可以减少装配时间和工作量，从而提供较高的生产率。在产品的装配工艺规划过程中，装配序列规划(Assembly SequencePlanning，ASP)是其核心部分，其优劣对产品的装配质量有直接影响[2-3]。因此，对于结构复杂、零部件数量众多的机翼来说，寻求一组较优的序列使得装配零部件组装在一起尤为重要。

目前，运用智能化方法装配体进行装配序列规划，已经成为装配工艺规划领域的热点问题。针对装配序列规划，国内外众多学者通过不同的智能化方法进行了研究。Wang D等[4]在天线反射板的装配中，通过遗传算法进行了装配序列规划；Mishra A等[5]提出了一种基于花授粉算法(FPA)的智能装配序列优化方法，该方法在满足各种优先约束条件下，通过最小化方向变化和刀具变化的次数，自动生成多个唯一的最优装配序列；Wu Y J等[6]利用粒子群算法完成了偏心铣床的装配序列规划；曲兴田等[7]提出一种混合循环算法，实现快速全局寻优，而后结合虚拟现实技术，增强人机交互性，从而对所得序列进行优化；L Xin等[8]采用一种新的编码方式，利用遗传算法完成卫星部分结构的装配序列规划，提高了全局搜索能力；Bala Murali Gunji等[9]提出了一种新的混合人工智能技术，该技术结合遗传算法实现人工免疫系统(AIS)，从而找到一种最优可行的算法从可能的装配序列中提取装配序列；Gunji A B等[10]提出基于TLBO的装配子检测方法来优化机器人装配序列规划。

上述方法对于具有曲面结构较多的飞机机翼的装配来说，并不能依照机翼的结构特点完成装配序列规划。本文在充分考虑飞机机翼组成特点以及零部件的设计，建立装配优先矩阵以及非正交干涉矩阵，增加装配方向完成装配的可行性分析。通过改进遗传算法的搜索策略，实现快速的全局寻优，完成机翼装配序列规划。

1 基装配序列规划矩阵模型

1.1 装配优先关系矩阵

在装配过程中，各零部件在空间存在一定的位置关系以及在工艺要求上存在一定的相互联系的逻辑关系，根据位置和工艺要求，零件的装配需要按照一定的优先顺序进行，零件间的这种关系即为装配优先关系。以矩阵Mp=[Rij]n×n的形式表达各零件间的关系有利于后续通过智能化算法进行求解。

(1)

其中，矩阵中元素的值分为两种情况：0和1。当Rij=0时，表示零件i和零件j之间不存在优先关系，即在装配过程中i不优先与j；当Rij=1时，表示零件零件i必须优先装配零件j。

1.2 装配非正交干涉矩阵

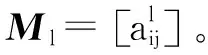
(2)

其中，l={±x，±y，±z，dk}((k=1，2，3…)为新增加的装配方向)。式中元素a的取值为0和1，若零件i与零件j按照装配方向l装配时不产生干涉，则取值为0；否则取值为1。

2 优化目标函数的建立

在求解的装配序列中，若该序列符合装配矩阵模型的约束，即视为该序列是有效的，但可行的装配序列并不一定是最优的，所以需要进一步的进行适应度值的计算。因此，需要建立一个满足装配任务的适应度函数，该函数需满足以下要求：

(1) 装配工具的变化

在产品装配过程中，不同的零件间的安装需要使用相对应的工具，往往在装配过程中需要根据零件进行更换。频繁的更换工具会影响装配进度，消耗时间，因此要尽量减少变更工具，减少时间浪费。

(3)

(2) 装配方向的变化

在产品装配过程中，零件间的装配应尽量减少装配方向的改变，频繁的改变装配方向会造成时间的浪费。因此在同一方向上，应尽可能的进行更多的装配操作。

(4)

结合式(3)和式(4)得到目标函数如下：

f=ω1ft+ω2fd

(5)

在式(5)中ω1、ω2是权重系数，且满足ω1+ω2=1。

3 遗传算法的改进

在标准的遗传算法中，初始种群的产生是随机的，并且在寻找最优目标的过程中，其搜索模式也是随机的。这样的操作没有针对性，较为浪费时间，而且算法的效率较低，使算法易陷入局部最优解。因此本文针对初始种群的生成进行改进，以及改进算法的搜索策略，以提高算法的搜索速度，得到最优的装配序列。

3.1 初始种群的生成

在算法中，初始种群的生成是依据装配序列的矩阵模型。根据装配优先矩阵和非正交干涉矩阵对初始种群进行筛选，求解出一些符合可行要求的装配序列。

(6)

式中，当Ft=0时，此装配序列符合要求，是可行的；当Ft≠0时，此装配序列不可行。

(7)

式中，当Fd=0时，此装配序列符合要求，是可行的；当Fd≠0时，此装配序列不可行。

通过式(6)和式(7)完成最后可行的装配序列的确定，以减少初始种群的随机性与盲目性，提高算法效率，初始序列的可行性判断过程如图1所示。

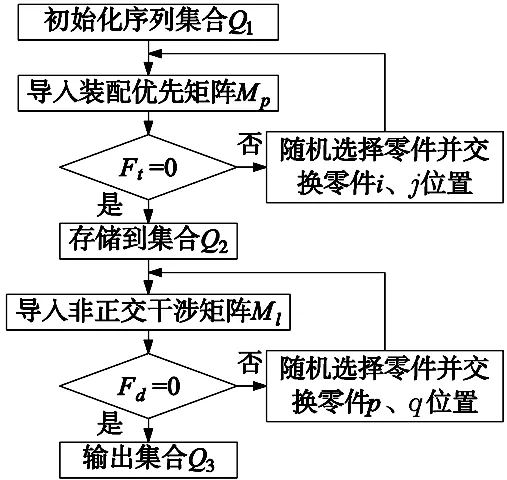
图1 初始种群获取流程图

3.2 搜索策略的改进

在传统的遗传算法中，每进行一次迭代寻找最优解的过程中，交叉和变异过程都是随机的，致使每次寻优都会产生大量重复和无用的解，浪费了求解的时间。如果不能有效的找到最优的解，还会导致算法陷入局部最优，因此重新设计了算法的交叉方式和变异形式，以增加算法寻优的搜索速度以及能力。

(1)交叉

在装配序列的交叉方式中，首先在可行的装配序列里选取两个个体作为父代p1、p2，在两父代上随机生成一个交叉点，将父代序列分别分为两个部分。然后，将p1的左部分直接作为子代序列c1的部分，再将p2序列中的基因未出现在c1里的按照顺序依次给予c1，从而生成完整的子代序列c1。最后子代序列c2也按照相同的方法生成。其操作过程如图2所示。

图2 交叉过程示意图

(2)变异

在变异过程中，变异点的位置是随机产生的，而在该位置是否产生变异是依据在变异点前后的零件装配是否存在约束关系。若二者存在约束关系，则向后顺延，并将其移至变异点后，其余零件依次排列。具体操作如图3所示。

图3 变异过程示意图

3.3 改进遗传算法的实现步骤

在产品的装配过程中，通过矩阵模型约束下得到初始种群，并利用改进的交叉模式和变异方式完成最有序列的输出，具体的求解步骤如下：

(1)初始化参数的设定：包括种群的大小、迭代次数以及交叉、变异的概率和产品零件的数量；

(2)根据遗传算法，随机产生初始种群；

(3)根据装配序列矩阵模型进行初始种群序列的可行性判断，筛选出符合条件的可行序列；

(4)计算每条序列的适应度值，并将值较小的序列存储，再进行交叉、变异操作。而值较大的序列则直接进行交叉、变异操作；

(5)判断是否达到预设的迭代终止条件，若没有则跳回步骤(3)；

(6)输出符合要求的最有装配序列。

4 实例验证分析

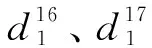
1,2.墙 3.梁 4,5,6,7,8.肋 9,10,11.连接板 12,13.桁条 14.油箱连接板 15.油箱盖板 16.机翼蒙皮1 17.机翼蒙皮2 图4 机翼结构图

对图4所示的机翼零件进行优先约束确定，并进行干涉分析，生成装配优先矩阵Mp和非正交干涉矩阵Ml。设置算法参数进行装配序列规划，种群大小M=100，迭代次数为100，交叉概率Pc=0.7，变异概率Pm=0.05。权重参数ω1=0.7，ω2=0.3。通过改进的算法进行求解，所得的最优装配序列为：{1，4，6，9，3，10，5，7，11，2，8，12，13，14，15，16，17}。

如图5所示是标准遗传算法和改进的算法对比图。由此分析可得到，通过建立矩阵模型，在种群初始化过程中可以有效的对装配序列进行优化，提高初始种群质量。对算法交叉和变异方式的改变，有效提高了算法搜索能力，加快了收敛速度。

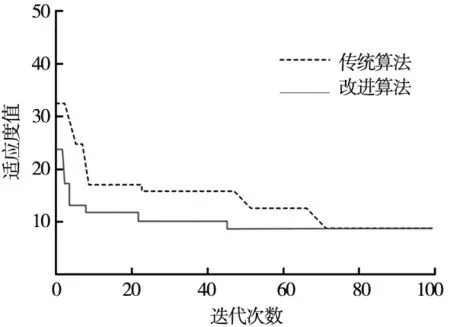
图5 算法结果对比图

5 结论

本文以飞机机翼为研究对象，分析机翼结构特点，通过建立机翼装配过程中零部件的装配优先约束关系，以及增加装配方向，扩大了装配过程的搜索范围，解决了机翼零部件在装配过程中受到具有曲面特征而影响装配干涉的问题，也减少了冗余的运算。同时，在装配中，以零部件的装配方向改变和装配工具为目标函数，通过建立新的交叉和变异方式，使传统的遗传算法在搜索效率上得到了较大的提升，从而可以高效的对最优的装配序列进行快速搜索。