回撤通道直接顶下沉量计算及其影响因素分析
2021-06-30王树帅王志强黄鑫苏泽华
王树帅,王志强,黄鑫,苏泽华
1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;
2.中国矿业大学(北京)能源与矿业学院,北京 100083
综采工作面的设备回撤是矿井生产的重要环节,目前设备回撤工艺主要有无预掘回撤通道、预掘单回撤通道和预掘双回撤通道3种[1]。回撤通道直接顶下沉量对设备回撤具有重要影响,因此确定回撤通道直接顶下沉量及分析其影响因素,对保证工作面贯通和设备回撤期间的安全具有重要意义[2]。
巷道围岩变形的形成机制一般分为3种[3-5]:一是上覆岩层传递给围岩的自重应力;二是由工作面回采导致围岩应力场的叠加;三是岩体本身强度较低。目前确定直接顶变形主要有理论分析、数值模拟和现场实测3种方法。
关于直接顶变形,公认的观点为基本顶对直接顶的给定变形[6-7]。钱鸣高等[6]推导了直接顶变形压力公式,分析了直接顶变形规律,得出直接顶变形与支架作用力无关,是基本顶作用其的给定变形;高峰等[7-8]、杨慧斌等[9]建立了回撤通道基本顶给定变形条件下直接顶的力学模型,运用能量原理及变分法对通道直接顶下沉量进行了求解,并探讨了顶板下沉量、支架工作阻力、直接顶高度、直接顶弹性模量及基本顶回转角之间的相互关系;万镇[10]建立了基本顶在支架后方断裂时直接顶力学模型,将其简化为一端固定的悬臂梁,建立梁的挠曲线近似微分方程并积分,求解出直接顶的转角和挠度;马新根等[11]对切顶卸压自成巷不同区域(煤体支撑区、动压承载区和成巷稳定区)的巷道直接顶,分别建立不同的梁力学模型,得到了不同类型的直接顶下沉变化量;王博楠[12]分别建立了贯通前基本顶三种不同断裂形式的直接顶简化力学模型,求解出了回撤通道顶板中心线处的下沉量,并对其影响因素进行了分析。
除理论分析外,数值模拟及现场实测[13-17]也是确定直接顶变形的重要手段。李全生等[13]、李永亮等[14]利用FLAC3D对煤层上覆岩层的变形及破坏规律进行了分析,并提出相应的支护方案;郝登云等[15]、单仁亮等[16]对巷道变形量进行了现场实测,总结了巷道变形规律,并制定了巷道变形监测评价体系;程占博等[17]结合现场实测、固支梁模型及数值模拟对顶板破断特征进行了分析。现场实测[15-18]准确度高,可参考性强,但所使用仪器结构复杂,现场操作烦琐,且使用环境条件要求较高,部分方法周期长、劳动强度大,因此并未全面推广。在现场条件限制下,理论分析及数值模拟成了很多学者选择的研究方法。
关于直接顶下沉量理论计算研究成果众多,但是基于基本顶断裂位置来分析回撤通道顶板下沉量的研究目前尚少,文献[12]虽建立了基本顶断裂后直接顶挠度力学模型,但是计算方法过于简单,考虑因素不全面。因此,本文采用直接顶梁理论,基于基本顶断裂位置,建立工作面贯通后回撤通道直接顶挠度力学模型,将支承应力简化为与其拟合的关于x的抛物线,利用悬臂梁挠度理论求取回撤通道顶板中心线处直接顶下沉量,并对其影响因素进行系统分析。
1 工程概况
1.1 研究对象
梧桐庄煤矿2号煤层三采区在末采阶段,只剩下182312(简称312)走向工作面,如图1所示。
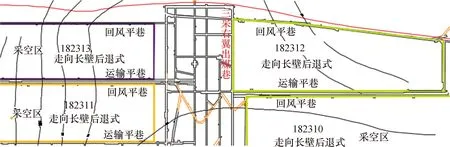
图1 182312工作面布置
在末采阶段,将312工作面直接贯通三采右翼出煤巷(简称出煤巷),将出煤巷作为312工作面支架的回撤通道。
1.2 基本顶断裂位置
工作面在贯通前,根据基本顶断裂位置与出煤巷的位置关系,基本顶最后一次断裂主要有图2所示的3种形式[19-20]:①基本顶在出煤巷左侧实体煤上方断裂;②基本顶在出煤巷上方断裂;③基本顶在工作面与出煤巷之间的剩余煤柱上方断裂。
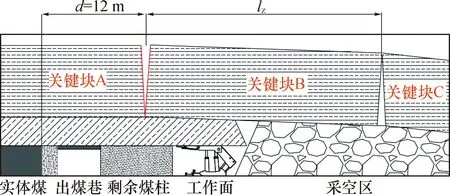
lz—基本顶周期断裂步距,平均为20 m;d—基本顶断裂位置与实体煤破碎区内边缘的距离,m
312工作面在贯通出煤巷前,基本顶最后一次实际断裂位置位于剩余煤柱上方,即d在12 m左右。
2 直接顶下沉量计算
建立工作面贯通后出煤巷直接顶挠度力学模型如图3所示[12]。由于支架后方采空区为矸石破碎区,破碎的矸石未接触直接顶,因此将直接顶简化为左端固支在实体煤帮的悬臂梁,利用悬臂梁挠度公式对顶板中心线处的直接顶下沉量进行计算。
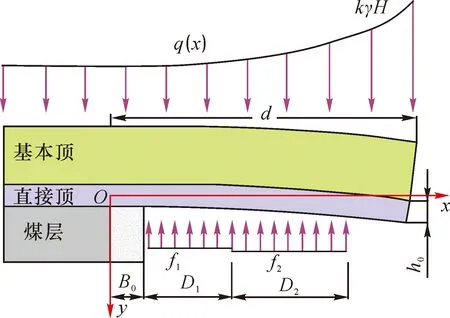
图3 回撤通道直接顶挠度力学模型
图3中,以出煤巷实体煤帮部塑性区左侧边缘为原点O;q(x)为支承压力,MPa;应力峰值为kγH,k为应力集中系数,γ为岩石容重,MPa/m;H为煤层埋藏深度,m;f1为出煤巷支护阻力,MPa;f2为支架工作阻力,MPa;D1为出煤巷跨度,m;D2为支架控顶距,m;h0为直接顶厚度,m;B0为实体煤帮部破碎区宽度,m。
支承应力q(x)表达式[21]为
(1)
式中,f为煤层内摩擦力;M为工作面采高;β为侧压力系数。
式(1)中q(x)函数形式比较复杂,对其进行积分和求解力的作用重心时,工作量大,且其重心不容易确定。因此,将支承压力q(x)简化为均匀荷载q1和连续递增到q2的n次抛物线形荷载。并将q2表达式简化为与其拟合的x的n(n取整数)阶函数,也即将q2应力曲线简化为关于x的n次抛物线,如图4所示。当d及n取不同值时,关于x的n阶函数通式可表达为
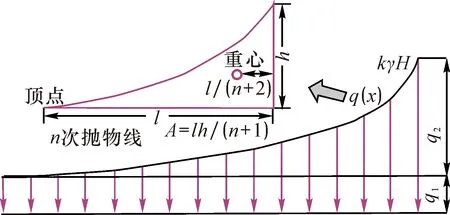
图4 支承应力拟合曲线
q2(xn)=λn(d-x)n
(2)
(x=0,1,2…d)
(3)
(4)
(5)
图4中,A、l及h分别表示抛物线的面积、长度和高度。
直接顶挠度由支承应力q(x)、出煤巷巷内支护力f1及支架支护力f2共同决定。x轴上任一点的弯矩及挠度公式由以下4部分决定:
(1) 均匀荷载q1作用下任一点弯矩M1为
(6)
由M1引起的任一点挠度w1为
(7)
(2) 连续变化荷载q2作用下任一点的弯矩M2为
(8)
由M2引起的任一点挠度w2为
(9)
(3) 出煤巷巷内支护力f1对任一点的弯矩M3为
(10)
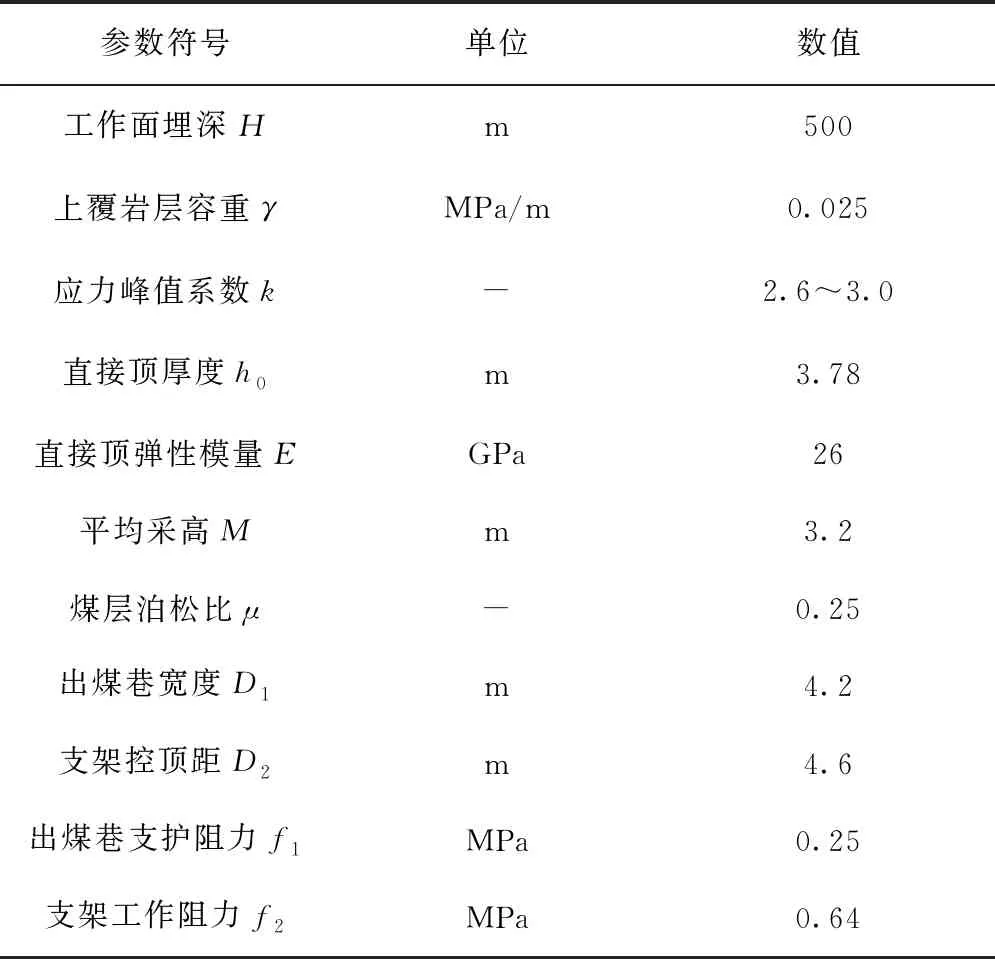
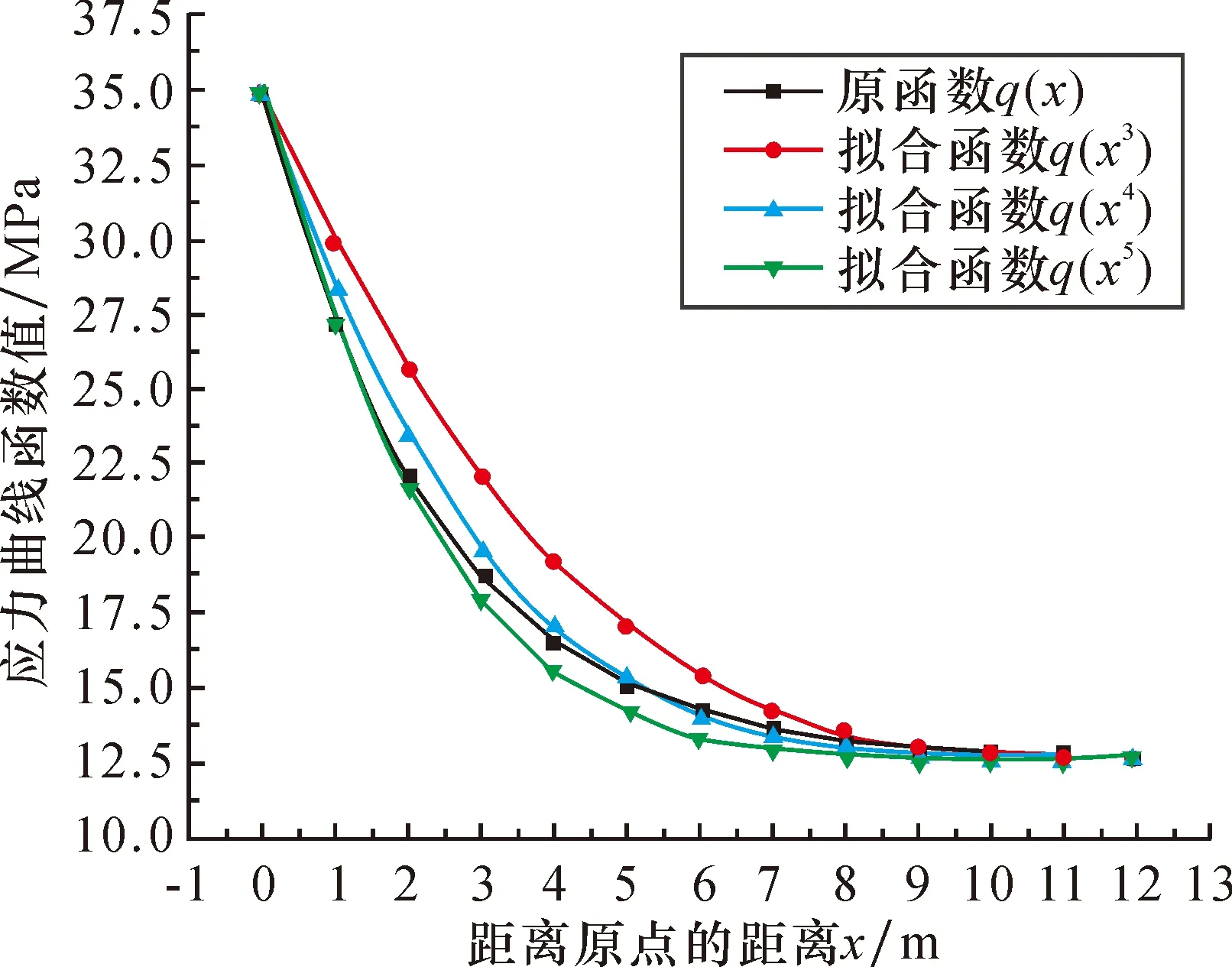
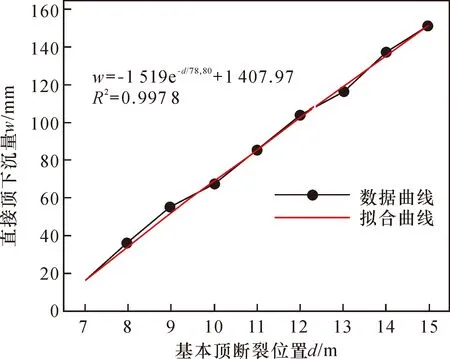
B0 由M3引起的任一点挠度w3为 (11) (4) 支架支护力f2对任一点的弯矩M4为 (12) 由M4引起的任一点挠度w4为 (13) 因此,直接顶任意位置的挠度w为 w=w1+w2+w3+w4 (14) 取x=(B0+D1)/2,即可得到出煤巷顶板中心线处直接顶挠度。 312工作面各地质及工程参数见表1。 表1 312工作面地质及工程参数 由上述各地质及工程参数计算得 B0=htan(45°-φ/2)=2.43 mf=tanφ=0.34β=μ/(1-μ)=0.33I=bh03/12=4.05 m4 支承应力q(x)曲线所对应x的抛物线的次数n随着断裂位置d的不同而发生变化。取d=(7~15,只取整数)。经拟合后发现:当d=7、8、9时,n=3;当d=10、11、12时,n=4;当d=13、14时,n=5;当d=15时,n=6。限于篇幅,结合基本顶贯通前最后一次断裂的位置,即d=12时,原函数与n次抛物线的拟合曲线对比如图5所示。 图5 应力曲线与抛物线拟合曲线对比 由图5知,当d=12时,与支承应力q(x)拟合效果最好的为x的4次抛物线,即n=4,q(x4)=12.628+1.08×10-3(12-x)4。因此根据式(14),计算得312工作面贯通后出煤巷顶板中心线处直接顶的下沉量为105 mm。在现场实际中,出煤巷在回撤期间,围岩未发生显著变形,为防止出煤巷发生局部冒顶或片帮等事故,在末采期间对出煤巷采取了一定的巷内补强支护措施。 本文直接顶挠度力学模型是基于基本顶不同断裂位置d建立的,d不同,支撑压力q(x)所拟合的x的n次曲线的n值也不同,则计算结果也就不同。绘制直接顶下沉量随d变化的数据曲线,并利用单相指数衰减函数对数据曲线进行拟合,基本顶断裂位置d的影响规律如图6所示。 图6 基本顶断裂位置d的影响规律 由图6可以看出,随着d增大,即随着基本顶断裂位置远离出煤巷,出煤巷直接顶下沉量随之增大,d在7~15 m区间内,下沉量由15.63 mm增加到151.67 mm,且呈近似直线趋势增加。基本顶断裂位置d对直接顶下沉量的影响非常显著,在实际生产过程中,应根据基本顶预断裂位置,采取合理的让压调节措施,使基本顶在合理位置断裂。 由第2章分析得,影响回撤通道顶板中心线处直接顶下沉量的因素主要有2类: (1) 地质因素。包括直接顶厚度h0;直接顶弹性模量E;煤层埋藏深度H;应力集中系数k;侧压力系数β煤层内摩擦角φ。 (2) 工程因素。包括出煤巷跨度D1;支架控顶距D2;巷内支护阻力f1;支架工作阻力f2;采高M。 图7、图8分别分析了地质因素和工程因素对回撤通道顶板中心线处直接顶下沉量的影响规律。实线表示直接顶下沉量,虚线表示直接顶下沉量随影响因素变化的单位变化量。 3.3.1 地质因素分析 由图7可知,影响出煤巷顶板中心线处直接顶下沉量的6种地质因素中,直接顶厚度h0、直接顶弹性模量E、煤层埋深H和应力集中系数k对直接顶下沉量的影响显著,影响程度分别为-685.886 mm(-96.95%)、-102.17 mm(-60.00%)、59.90 mm(80.04%)、57.13 mm(72.48%),其中直接顶厚度h0和直接顶弹性模量E的影响最为显著,煤层埋深H和应力集中系数k影响较为次之;侧压力系数β和煤层内摩擦角φ的影响较小,分别为-20.24 mm(-19.32%)和8.97 mm(9.36%)。 煤层埋深H和应力集中系数k的影响规律相似,随着两者的增大,顶板下沉量都增加;顶板下沉量单位变化量随着两者的变化几乎呈一条水平直线,无明显变化。因此,顶板下沉量随着煤层埋深H和应力集中系数k呈近似直线增加;而直接顶厚度h0、直接顶弹性模量E和侧压力系数β的增加,对顶板的下沉量均呈抑制作用,随着三者的增加,单位变化量分别呈“前期快速减小、后期无明显变化”“逐渐减小”和“前期无明显变化、后期突然增大”的趋势。随着煤层内摩擦角φ的增大,顶板下沉量呈现先迅速增加后缓慢减小的趋势,但整体表现为增加趋势,单位变化量由9 mm迅速减小至0 mm附近,且后期无明显变化。 综上所述,各地质因素对直接顶下沉量均具有一定的影响,其中直接顶厚度h0和弹性模量E对顶板下沉量影响最大,也即直接顶自身性质对直接顶的下沉量起着关键性作用。 3.3.2 工程因素分析 由图8可知,在本文中影响顶板下沉量的5种工程因素中,只有回撤通道跨度D1的影响效果显著,随着D1的增加,顶板下沉量逐渐增加,增加了65.02 mm(80.68%),且单位变化量逐渐增加。其余4种因素的影响效果非常微弱,顶板下沉量的总变化量均在5 mm以内。 相比而言,地质因素较工程因素对顶板下沉量的影响更加显著,也即地质因素是决定顶板下沉量的根本因素;而工程因素中,回撤通道跨度D1的影响较为明显,因此在设计掘进回撤通道时,在保证设备顺利回撤的前提下,可适当减小回撤通道跨度。在本文中,出煤巷作为回撤通道,跨度已确定。结合地质因素和工程因素的影响效果可知,回撤通道顶板直接顶变形是给定变形,通过巷内支护和支架来改善直接顶变形,效果是微弱的,但可以控制顶板局部冒顶。 工作面在末采阶段,采用“十字布点法”,对出煤巷的变形量进行实时监测。测站布置如图9所示。 图9 测站位置布置示意图 在出煤巷布置3个测站,分别距312工作面运输平巷30 m、130 m、230 m,监测回撤通道顶底板和两帮相对移近量以及通道底鼓量。监测结果如图10所示。 图10 测站数据曲线 由图10可知,测站1顶底板最终移近量为0.293 m,两帮最终移近量为0.382 m,底鼓量最终为0.168 m;测站2顶底板最终移近量为0.312 m,两帮最终移近量为0.408 m,底鼓量最终为0.184 m;测站3顶底板最终移近量为0.276 m,两帮最终移近量为0.357 m,底鼓量最终为0.153 m。 巷道变形量随着工作面与出煤巷距离的减小而变大,在20 m之前,巷道变形量几乎无变化,说明此过程中出煤巷未受到工作面超前应力的影响,煤柱及出煤巷相对稳定;在20~7.5 m之间,巷道变形量开始较小量地增加,说明此过程中出煤巷与工作面应力开始叠加,出煤巷受到工作面超前应力影响,变形量开始增加,但增加量较小,增加速度缓慢,此过程煤柱仍处于弹性状态;在距离7.5 m处出现拐点,变形量突增,可推断在此处出煤巷与工作面应力峰值开始叠加,应力达到峰值,煤柱开始进入塑性状态,承载力变低,出煤巷变形量明显增加。且测站2变形量大于其他两个测站的,说明工作面中部应力对巷道影响最严重。理论计算与现场实测结果相吻合,说明了直接顶挠度力学模型具有一定的可靠性。顶底板及两帮最大移近量分别为0.312 m和0.408 m,变形量均在巷道尺寸的10%以内,顶板下沉量在0.123~0.128 m之间,未出现强烈矿压显现,整个贯通阶段回撤通道比较稳定。 (1) 本文基于基本顶断裂位置d建立了312工作面贯通后回撤通道直接顶挠度力学模型,计算得三采右翼出煤巷顶板中心线处的直接顶下沉量为105 mm,且下沉量随着d的增大呈近似直线增加,基本顶断裂位置d对直接顶下沉量具有关键性影响。 (2) 分析了直接顶下沉量随影响因素的变化规律,即直接顶厚度h0、弹性模量E、煤层埋深H、应力集中系数k及回撤通道跨度D1的影响效果显著,其余因素影响甚微。 (3) 结合各因素对直接顶下沉量的影响结果,地质因素是影响其变化规律的主控因素。同时,验证了直接顶变形是给定变形,通过巷内支护和支架来控制直接顶变形,效果是不明显的,但可以控制顶板局部冒顶。 (4) 采用“十字布点法”对三采右翼出煤巷变形量进行了现场监测。在整个贯通阶段,顶底板和两帮最大变形量分别为0.312 m和0.408 m,顶板下沉量在0.123~0.128 m之间,未出现较严重的矿压显现。理论计算与现场实测具有一定的吻合性。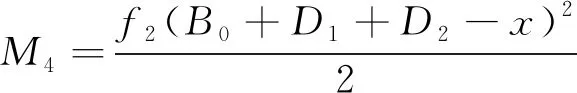
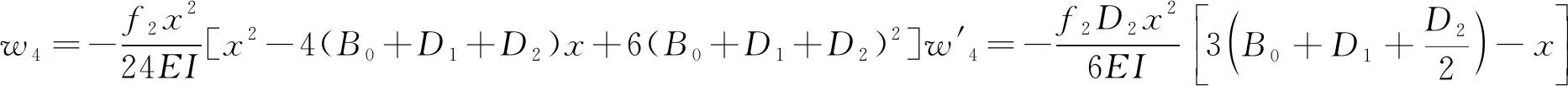
3 工程计算及影响因素分析
3.1 工程计算
3.2 基本顶断裂位置d的影响
3.3 回撤通道顶板下沉量影响因素分析
4 回撤通道位移监测


5 结 论
