考虑微观孔隙几何的砂岩自发渗吸理论模型
2021-06-30董川龙滕腾李志虎张文涛
董川龙,滕腾,李志虎,张文涛
1.中国矿业大学(北京)能源与矿业学院,北京 100083;2.山西大同大学煤炭工程学院,山西大同 037003
自发渗吸是普遍存在于岩石、土体、水泥、陶瓷、电极、砖体等材料[1]微观孔隙结构中的一种水动力现象,驱动力来源于微小孔隙(10-2~102μm)产生的毛细管压力,属于非饱和渗流研究的范畴。多数情况下,自吸的水分以及内部的离子会降低材料的力学特性或间接地渗透污染地下水源,需要防止或减弱渗吸行为;少数情况下,能源开发中富集于储层微小孔洞内的油气多通过自发渗吸将其驱替出来,需要增强或促进渗吸行为。因此,研究岩石自吸机理对于岩体工程具有重要意义。
岩石自发渗吸的研究手段主要有理论模型与室内实验。室内实验仅能观察吸水过程的一些表象规律,并不能揭示渗吸过程的内在机理。据此,众多研究者基于一定的简化模型与条件假设,从内在机理出发建立了可以描述自吸行为的理论模型,目前比较经典的理论有Lucas-Washburn(LW)模型[2-3]、Terzaghi 模型[4]、Handy模型[5]。后期大量学者对上述模型做了修正。
LW模型由于其从毛细管水动力学特征出发描述多孔介质的吸水特性,同时其认为吸水表征量与时间平方根成正比,比较符合实验室尺度所观测到的规律现象以及孔隙结构吸水的动力学特征,因此被众多研究者应用。LW模型将孔隙结构简化为不同尺寸直线延伸且等圆截面的毛细管束,而大量研究者通过微观成像发现,实际孔隙结构中存在通道弯曲、截面极不规则和随处变化、孔隙尺寸分布不均等特征(图1),因而LW模型在实际应用中有较大局限性。针对上述问题,Dullien等[6]考虑孔隙结构的孔吼特征,引入孔隙迂曲度的概念,定义了描述自吸水力特性的表观孔隙直径。Lundblad等[7]在研究电极材料自吸特性时,定性地引入包含孔隙迂曲特性的有效孔隙半径的概念。Benavente等[8]和Cai等[9]引入孔截面形状因子与孔隙结构迂曲度对LW模型进行了修正,二者不同的是,Benavente等[8]仅仅靠经验直接引入修正因子,而Cai等[9]进行了严格的数学推导,其他学者也有类似修正[10]。值得注意的是,Cai模型中认为孔隙几何形状修正因子大于1,与实际物理意义不符。
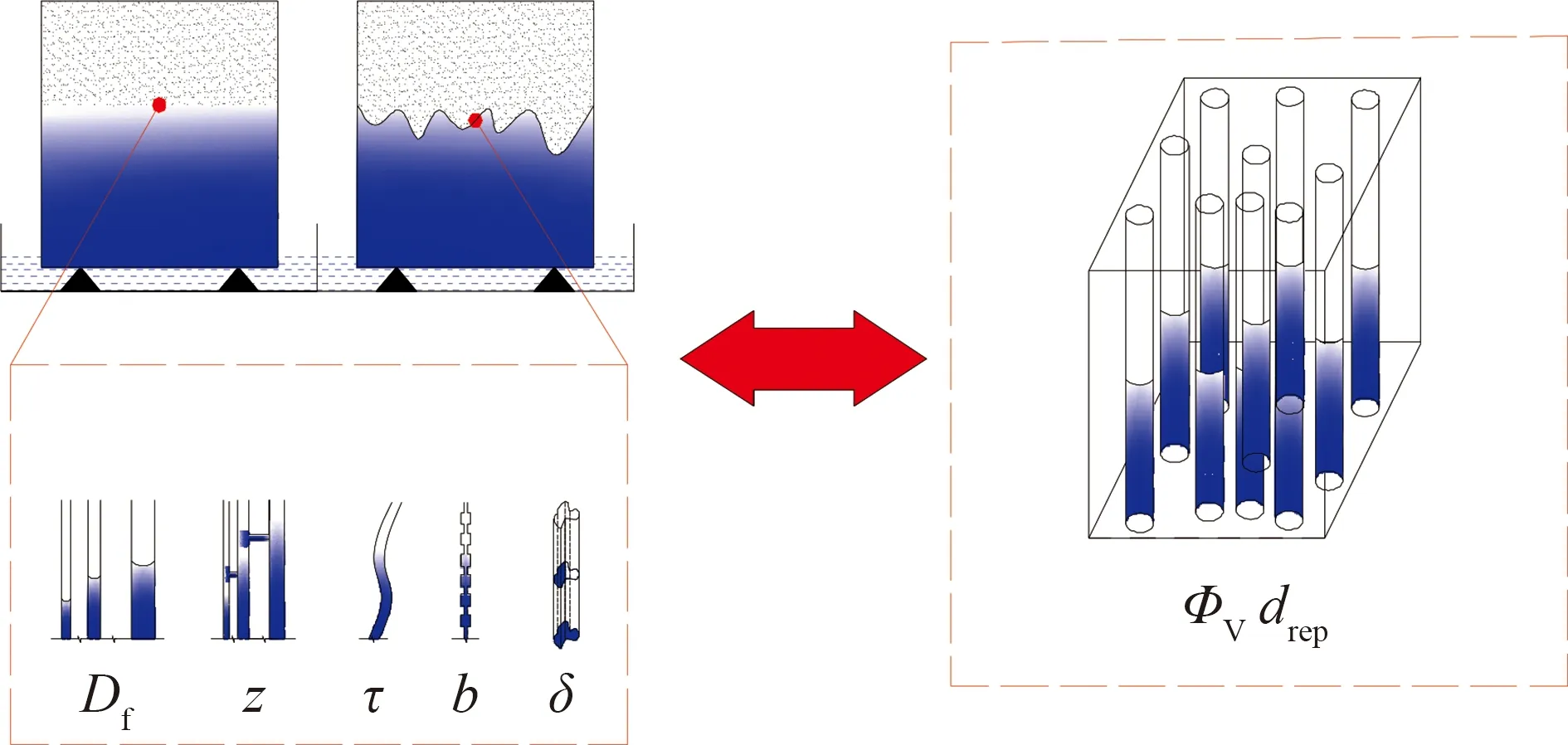
Df—孔隙尺寸分布分形维数;z—孔隙拓扑结构配位数;τ—孔隙结构迂曲度;b—孔吼单元体孔吼比;δ—孔隙截面不规则形状几何因子;ΦV—孔隙结构体积孔隙率;drep—等效毛管束水力直径。
本文针对上述模型中的缺陷,引入孔隙形状修正因子与孔隙结构迂曲因子,经数学推导得到以平均几何与分形几何分别表征的砂岩吸水理论模型,并应用前人的实验数据对模型的有效性与适用性进行了验证和分析,对孔隙结构几何参数影响吸水敏感性进行定量分析,对比了2种模型的优缺点。本研究成果可为砂岩型油气储层采用自发渗吸进行二次增强型回采提供理论指导。
1 修正的H-P方程及L-Y方程
天然多孔介质微观孔隙结构较复杂,孔隙几何常呈现不规则形态,且连通孔隙曲折迂回。为真实建立描述多孔介质吸水性的动力学方程,首先引入描述不规则孔隙的定量指标形状因子δ对Hagen-Poiseuille (H-P)方程、Laplace-Young (L-P)方程进行修正;其次引入描述连通孔隙曲折迂回的定量指标迂曲因子τ对H-P方程进一步修正。
1.1 考虑形状因子的H-P及L-Y方程修正
直线延伸且截面为圆形的毛细管吸水动力学行为可由H-P方程描述如下:
(1)
式中,q为毛细管体积流率,m3/s;d为毛细管直径,m;μ为动力黏度系数,N·s/m2;Ls为毛细管直线长度,m;Δp为水力压差,Pa。
对于两端开口的毛细管,式(1)中水力压差Δp可表示为
Δp=pc-ph=pc-ρgh
(2)
式中,pc为毛细管压力,Pa;ph为静水压力,Pa;ρ为吸入液相密度,kg/m3;g为重力加速度,m/s2;h为管中弯液面所在位置的垂直高度,m。
根据L-Y方程,圆管中毛细管压力为
(3)
式中,σ为气-液界面张力,N/m;θ为固-液接触角,(°)。
文献[11-14]考虑非圆形几何形状对H-P方程进行了通道截面的修正,Franken等[15]引入几何因子修正了不规则形状孔隙的L-Y方程。
水力直径的概念已经被用于描述非圆截面管道的水力特性,即
(4)
式中,dh为管道水力直径,m;A为管道横截面积,m2;P为管道截面周长,m。
Benavente等[8]定义孔隙几何形状因子为不规则形状截面水力直径与其等效圆形截面(二者面积相等)水力直径的比值:
(5)
式中,δ为孔隙几何形状因子;dih为不规则截面水力直径,m;dch为圆截面水力直径,m。
δ位于0到1之间,用于描述不规则截面偏离圆形的程度;越不规则的截面,δ越小;对于圆形、正方形、等边三角形,截面δ分别取1、0.776、0.886。此外,表征岩石孔隙尺寸的物理手段(MIP)与图像手段(X-Ray CT),一般是将孔结构等效为规则圆形截面的毛细管或者球棒模型,因而,所测得孔隙尺寸实则是等效圆形截面或球形立体的直径de。而对多孔介质进行吸水特性研究时,完全视孔隙结构为圆形通道是不合理的。需要对所测得等效直径de乘以几何形状因子δ代入式(1)和式(3)中进行必要修正,使其能更加准确地描述岩石孔隙结构的吸水特性。即
(6)
(7)
截面不规则的毛细管产生的黏滞阻力较圆截面毛细管要大,消耗能量较多,导致体积流量减少。截面几何形态越不规则,偏离圆形程度越大,即几何形状因子δ越小,体积流量越小,这从物理意义上解释式(6)中δ在0到1之间是合理的。
不规则截面几何形态一般存在内角,且形状越不规则,内角越多。圆形截面管壁上液面处于同一高度,而不规则形态内角附近液面比壁面其他部位偏高,导致不规则截面平均曲率大于圆形截面[17],驱动液体流动的毛细管压力相应较大,这也从物理意义上解释式(7)中δ在0到1之间合理。
1.2 考虑迂曲因子的H-P方程修正
岩石等多孔介质微观孔隙通道是弯弯曲曲的,可用迂曲度定量表征连通孔隙的弯曲程度,即
(8)
式中,τ为毛细管迂曲度;Lf为毛细管实际迂曲长度,m;Ls毛细管两端直线距离,m。
Dullien等[6]认为各种岩石孔隙结构具有相同迂曲度经验值为3,而Comiti和Renaud[16]基于颗粒填充床渗流实验得出,平均迂曲度与孔隙率之间满足如下关系式:
τav=1-Flnφ
(9)
式中,τav为颗粒填充床平均迂曲度;F为实验拟合常数,在0.5~1之间,对于球形颗粒与立方颗粒分别取0.41、0.63;φ为颗粒填充床孔隙率。
考虑管道迂曲特征,引入迂曲度τ进一步修正式(6)得
(10)
迂曲的毛细管产生的黏滞阻力较直毛细管要大,上升到相同高度消耗的能量较多,导致体积流量减少。孔隙通道越迂曲,即毛细管迂曲度τ越大,体积流量越小,这从物理意义上解释式(10)中τ取值大于1合理。
2 修正的LW吸水模型
Lucas与Washburn将多孔介质孔隙结构简化为毛细管束,发展了被后来学者广泛应用的描述多孔介质吸水行为的LW方程:
(11)
式中,Wsp为单位面积累积吸水质量,kg/m2。
LW方程仅考虑孔隙尺寸与孔隙率2个与孔隙结构相关的参量,与真实孔隙结构偏差较大,因而预测结果偏高实验值。针对该问题,本文应用平均几何与分形几何两种方法,引入几何因子与迂曲因子对LW方程进行了改进。
2.1 平均几何表征的吸水模型
根据管道流质量守恒定律,有
(12)
根据式(8),有
(13)
式中,vf为弯曲毛细管内实际速度,m/s;vs为毛细管内直线速度,m/s;vfav为考虑迂曲特征的实际流线平均运移速度,m/s;vsav为流体垂直侵入的平均表观速度,m/s。
联立式(2)、式(7)、式(10)、式(12)、式(13),可得单根毛细管垂直自发渗吸水动力学控制方程如下:
(14)
假设孔隙结构是由n根不同尺度且迂曲的毛细管组成,且各毛细管横截面形状是一致的,则水分平均速度可以表示为
(15)
式中,ni为直径dei孔隙的数量;vsi为直径dei孔隙内的水分移动速度,m/s。
将式(15)代入式(14),应用均一化思想,可得多孔介质内水动力学控制方程:
(16)
式中,deav为平均有效孔隙直径,m;Lsav为水头深度,m。
假设毛细管模型润湿端面后孔隙完全饱和,且介质润湿为活塞式驱替[24],则有
Wsp=φpρLsav
(17)
式中,φp为面积孔隙率。
将式(17)两边对时间进行求导,然后代入式(16),可得单位面积质量流率表达式如下:
(18)
Cai等[18]认为迂曲毛细管束体积孔隙率φV与面积孔隙率φp之间需满足:
φV=τavφp
(19)
一般平均迂曲度τav大于1,而直毛细管束有体积孔隙率等于面积孔隙率。
多孔介质渗吸初期,毛细管压力远大于重力,对自发渗吸起控制作用,忽略式(16)、式(18)右端重力项,并引入式(19)进行积分运算,可得考虑孔隙几何形态的修正LW自吸模型。
(20)
(21)
式中,C为比例系数,定义为毛细管系数,m/s0.5;S为比例系数,定义为吸水性系数,kg/(m2·s0.5);δ、τav均是无量纲量。
进一步引入用于描述水力特性的代表性孔隙直径drep(drep=ξdeav)的概念,drep综合反映了截面形状、迂曲程度、孔隙分布等微观几何特征对自发渗吸的影响程度,截面形状越不规则,孔隙通道越迂曲,drep越小,孔隙介质越难吸入润湿相。
2.2 分形几何表征的吸水模型
众多研究者发现沉积岩在一定观测尺度ε内,孔隙尺寸分布具有统计自相似性,即孔隙尺寸分布具有分形特征。假设孔隙结构具有分形特征,尺寸越小的孔隙数量越多,而尺寸越大的孔隙数量越小。引入形状因子δ,有如下关系式成立:
-dN=Df(δλmax)Df(δλ)-(Df+1)d(δλ)=Df(λmax)Df(λ)-(Df+1)dλ
(22)
式中,-dN为位于λ~λ+dλ之间的孔隙数量,负号表示孔隙数量随孔隙尺寸增大而减少;Df为孔隙尺寸分布的分形维数;λmax为最大孔隙尺寸;λ为任意孔隙尺寸;dλ为孔隙尺寸微增量。
结合式(2)、式(7)、式(10)可得考虑截面形状与弯曲程度的修正单根毛细管体积流量表达式:
(23)
式中,q(δλ)为不规则截面迂曲毛细管体积流量,m3/s。
结合式(22)、式(23),从最小孔隙尺寸λmin到最大孔隙尺寸λmax积分,用孔隙结构平均迂曲度τav代替单根毛细管迂曲度τ,用润湿端平均侵入孔隙介质深度Lsav代替单根毛细管侵入深度Ls,总体积流量表达式为
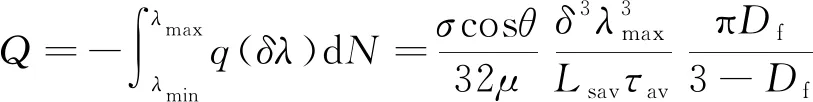
(24)
式中,β为最小孔隙尺寸与最大孔隙尺寸比值。
对于分形孔隙结构,有[21]
(25)
横截面总孔隙面积表达为
(26)
结合式(24)、式(26),应用质量守恒定律,可得多孔介质吸入水分垂直运移的平均速度表达式为
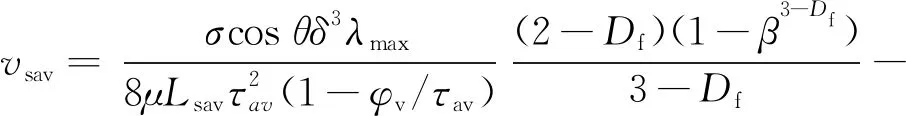
(27)
根据式(17),单位面积多孔介质累积吸入质量速率表达式为
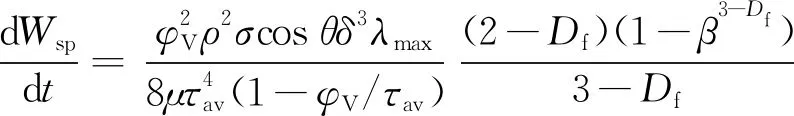
(28)
同理,渗吸初期毛细管压力起主要控制作用。忽略式(27)、式(28)右边的重力项,简化并积分,可得描述自吸水动力学的分形控制方程如下:
(29)
(30)
2.3 综合分析
对于同一种多孔介质吸入同一种液相,式(20)、式(29)的比例系数是相同的,联立式(20)、式(29)得等效平均孔隙直径的物理表达式如下:
(31)
式(31)表明,等效平均孔隙直径deav与二维分形维数Df、孔隙尺寸分布β、体积孔隙率φV、孔隙通道平均迂曲度τav、最大孔隙尺寸λmax有关。可以看出,最大孔隙尺寸越大的孔隙结构,其等效平均孔隙直径deav相应越大。
孔隙结构迂曲度与其介质孔隙率有关,孔隙率越小,迂曲度越大,孔隙结构各向异性越强,对应比值φV/τav越小,则等效平均孔隙直径deav越小。二维分形维数Df为面积分形维数,在1~2之间,可以定量表征孔隙结构的非均质特性。Df越大,孔隙结构非均质性越强,则等效平均孔隙直径deav越小。
3 结果与讨论
3.1 模型与实验的验证和分析
本吸水模型是在Benavente模型与Cai模型的基础上,考虑孔隙形状不规则性以及孔隙通道弯曲特性,对LW模型做了更为详细和全面的改进后的模型。
(1)本模型严格区分了体积孔隙率与面积孔隙率之间的差异,仅仅在孔隙结构平均迂曲度等于1的情况下二者是相同的。多数情况下因平均迂曲度大于1,使得体积孔隙率偏大于面积孔隙率。
(2)本模型导出初始,用小于1的孔隙几何形状因子修正了H-P方程与L-Y方程,其物理意义明确,完全能解释孔隙截面几何不规则性对其水力特性的影响效果,且后续数学导出过程更为严谨。
(3)本模型认为孔隙结构平均迂曲度与其固体颗粒排列方式、固结多孔介质孔隙率有关,不同种类的岩石其孔隙率以及颗粒胶结组合方式千差万别,并不能取固定经验值3。
下面应用实验数据对本模型的有效性、适用性、准确性加以验证分析,并论证本模型与已有模型的差异性、优缺点,以及需要进一步改进的地方。
3.1.1 Benavente模型所用实验数据分析
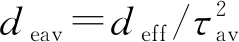
(32)
式中,rav为孔隙空间平均半径,m。
将上述参数分别代入式(21)和式(30)中,计算吸水性系数Spg与Spf。根据已有研究经验[8],模型中接触角取0°,σ、μ分别取0.0728 N/m、0.001 N·s/m2(下同)。同时将Benavente模型计算所得吸水性系数SB以及其实验所测得吸水性系数Sex同时列出,与本模型所获得的吸水性系数做对比分析(表1和图2)。需要注意的是,对于试样BR-1求Spf时取迂曲度拟合值τav=3,其余试样计算Spg与Spf均取F=0.6。Re为理论预测值的相对误差(下同)。
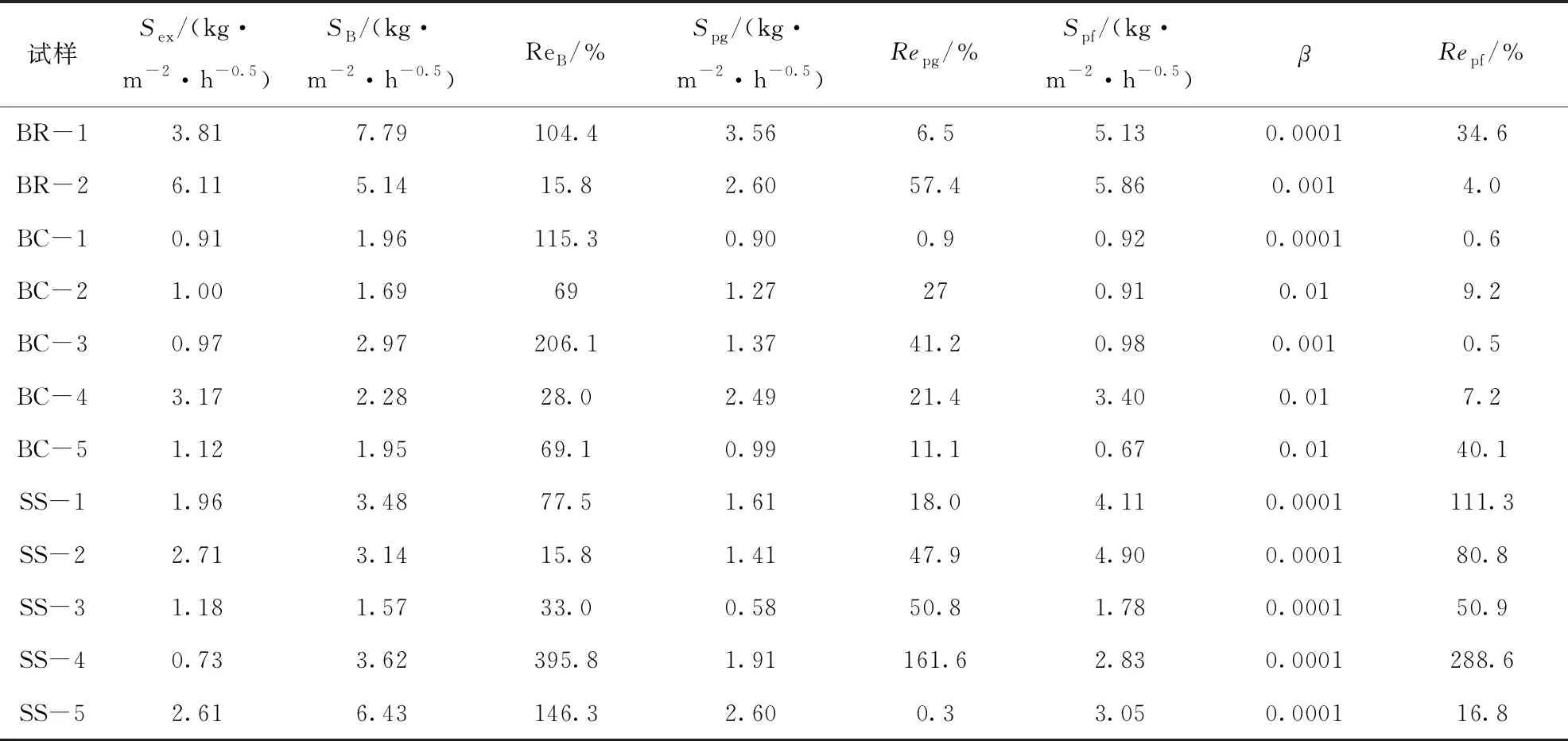
表1 模型计算参数以及计算所得吸水性系数
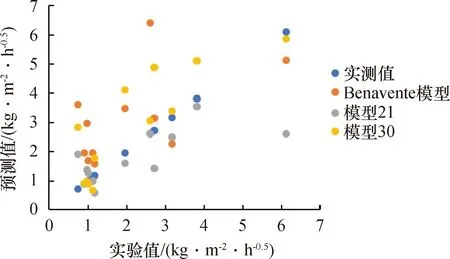
图2 模型预测值与实验值的对比
由表1和图2中可以看出,Benavente模型总体上除试样SS-2、SS-3以外,理论预测的吸水性系数与实验的吸水性系数偏差较大,试样BR-1、BC-1、BC-3、SS-4、SS-5相对误差均超过100%。相比而言,式(21)、式(30)对于10种岩石试样理论预测的吸水性系数相对误差要优于Benavente模型,试样BC-1、BC-3、SS-5相对误差小于1%,预测值基本与实验值相同;试样BR-1、BR-2、BC-2、BC-4相对误差小于10%;试样BC-5、SS-1相对误差小于20%。另外,试样SS-4的3种模型预测相对误差均超过100%,但是本模型预测值更接近于实验值。
综上所述,本模型对于所选取的12种不同矿物质地、不同矿物组分、不同孔隙结构岩石试样中的10种试样的吸水特性预测比较准确,且相对误差均在20%以内,验证了本模型的可靠性与普适性。Benavente模型理论预测值高估吸水性系数,可能是由于其没有严格区分体积孔隙率与面积孔隙率的差异,且直接引入修正系数,也没有严格的数学推导,结果是表征孔隙结构的等效水力直径与迂曲度的一次方成反比且与形状因子一次方成正比。而本模型与迂曲度的四次方成反比,且与形状因子三次方成正比。Benavente模型取孔隙结构迂曲度为经验值3,这在一定程度上可能高估某些岩石试样孔隙的实际迂曲程度。
3.1.2 Pia模型所用实验数据分析
本模型计算参数孔隙截面形状因子δ取Benavente模型中12种岩石试样实测平均值0.531,体积孔隙率φV、平均孔隙半径rav取Pia模型[22]中实测值,迂曲度、分形维数、最大孔隙尺寸是通过式(9)、式(25)、式(32)计算获取。将以上参数分别代入式(21)、式(30)计算吸水性系数Spg与Spf。同时,将Pia模型计算所得吸水性系数SIFU以及其实验所测得吸水性系数Sex同时列出,与本模型所获得的吸水性系数做对比分析(表2和图3)。所有试样δ=0.531,试样S7取τav=3,试样S5求取Spg取τav=3,其余情形均取F=0.6。
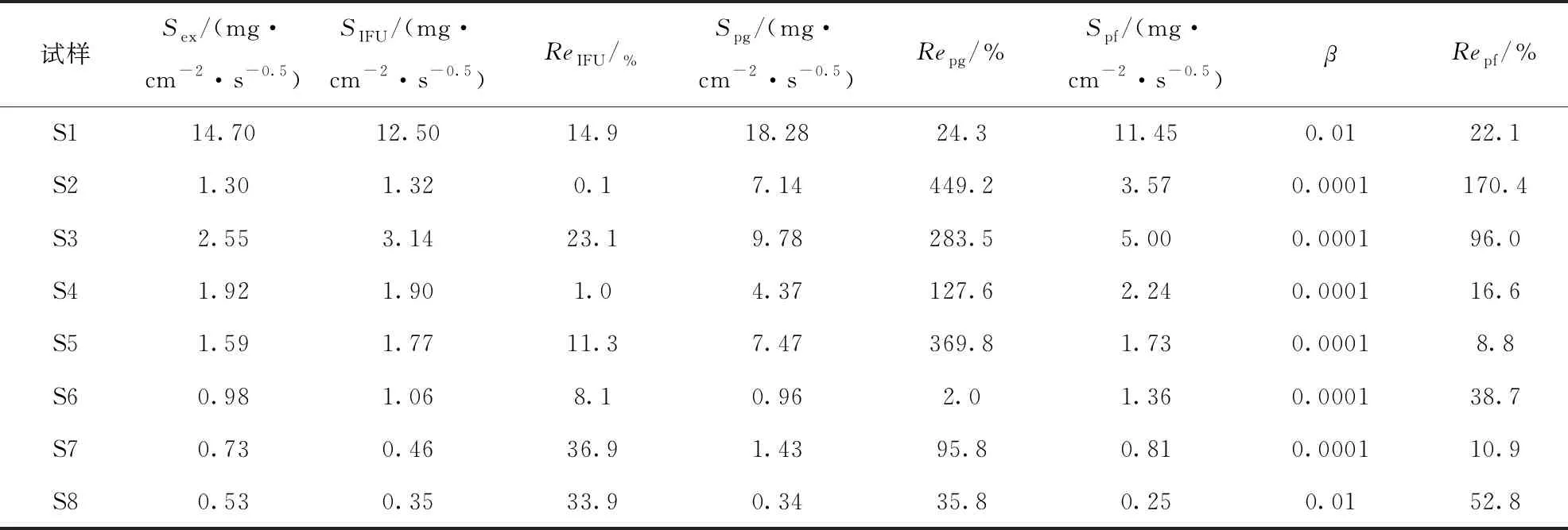
表2 模型计算参数以及计算所得吸水性系数
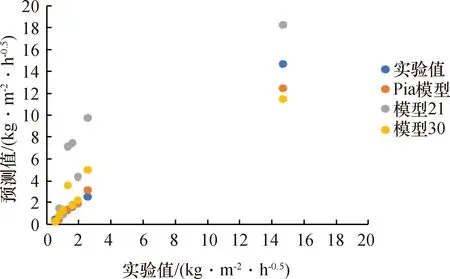
图3 模型预测值与实验值的对比
由表2和图3可以看出,除试样S1、S6、S8以外,相比实验值与Pia模型预测值,本模型理论预测值均高估了吸水性系数值,试样S2、S3相对误差均超过100%。可能原因是:一方面MIP法因汞压力的限制所测最小孔隙尺寸有限,而大多研究者认为微观孔隙结构中小孔隙数量占比多,实际可能高估了孔隙结构的平均孔隙半径;另一方面,孔隙形状修正因子取经验值0.531,有可能会低估实际孔隙截面几何形状的不规则程度。试样S8,本模型预测值低于实验值,取0.531可能高估了孔隙形状的不规则性;试样S6、S7,本模型比Pia模型更能精确预测吸水性系数;试样S1、S5、S8,本模型理论预测值基本接近Pia模型的;试样S4,本模型理论预测值相对误差控制在20%以内。
综上分析,8种岩石试样有6种岩石试样吸水性系数可以通过本模型加以准确预测,验证了模型的可靠性与普适性。值得注意的是,Pia模型[22]计算程序相对烦琐,需要借助计算机程序进行计算,而本模型相比Pia模型具有优越性,其几何解析方程简单明了,便于理解与应用。
3.2 孔隙结构几何参数敏感性分析
取孔隙率为0.2,平均等效孔隙直径分别为0.05 μm、0.5 μm、1 μm、5 μm,研究孔隙截面几何形状、孔隙通道弯曲程度对其吸水特性的影响规律,将相关参数代入式(21)中,可得反映截面形状与通道迂曲对孔隙结构吸水性系数的影响规律(图4)。其中,图4(a)图注为(孔隙直径,形状因子),图4(b)图注为(孔隙直径,迂曲因子)。

图4 孔隙迂曲因子与形状因子影响吸水性系数规律
由图4看出,孔隙截面几何形状与孔隙通道迂曲程度对孔隙结构吸水特性有重要影响。吸水性系数随迂曲度增加呈现非线性减小的趋势,且减小幅度逐渐降低,如图4(a)所示。吸水性系数随形状因子增加呈现非线性增加的趋势,且增加幅度逐渐增大,如图4(b)所示。孔隙截面越不规则,即形状因子越趋近于0,孔隙结构吸水性系数越小,越难吸入水分。同样,孔隙通道越迂曲,即迂曲度越大于1,孔隙结构吸水性系数越小,越难吸入水分。
平均等效孔直径从0.05 μm到5 μm跨越两个数量级,相同迂曲程度、截面形状下吸水性系数大约增加了10倍,而迂曲程度、截面形状从最小值变化到最大值,同等数量级下吸水性系数变化约25倍与31倍。可见,在孔隙截面极不规则、孔隙极其迂曲的孔隙结构中,孔隙空间尺寸对吸水特性影响较小,这也证实了实验观察到平均孔径较大的孔隙结构,吸水性系数反而较小。
取孔隙率为0.1,最大可渗孔隙直径分别为0.1 μm、3 μm、10 μm、40 μm,研究孔隙结构非均质性、各向异性对孔隙结构吸水特性的影响规律,将相关参数代入式(31)中,可得非均质性(Df)、各向异性(τav)对孔隙结构平均等效孔隙直径deav的影响规律(图5)。其中,图5(a)图注为(孔隙直径,分形维数),图5(b)图注为(孔隙直径,迂曲因子)。
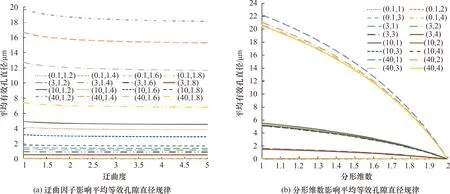
图5 孔隙迂曲因子与分形维数对平均等效孔隙直径影响规律
取最大可渗孔隙直径为10 μm,孔隙率分别为0.15、0.20、0.30、0.40,研究孔隙结构非均质性、各向异性对孔隙结构吸水特性的影响规律,将相关参数代入式(31)中,可得非均质性、各向异性对孔隙结构平均等效孔隙直径deav的影响规律(图6)。其中,图6(a)图注为(孔隙率,分形维数),图6(b)图注为(孔隙率,迂曲因子)。
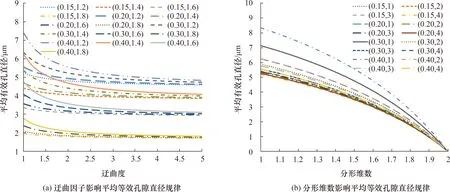
图6 孔隙迂曲因子与分形维数对平均等效孔隙直径影响规律
由图5、图6看出,孔隙结构非均质性与各向异性对其吸水特性均有影响。平均有效孔直径随迂曲度增大而呈非线性减小,且减小幅度逐渐呈现减少的趋势;平均有效孔直径随分形维数增大同样呈非线性减小,而减小幅度逐渐呈增大的趋势,即孔隙结构非均质性与各向异性越强,吸水能力越弱。值得注意的是,非均质性比各向异性对孔隙结构吸水特性影响更多,在低孔隙率与孔尺寸情况下,孔隙结构各向异性对平均有效孔直径基本无影响;随着孔隙率与孔尺寸逐渐增大,影响逐渐增强,但效果不是很显著。
最大可渗孔直径与体积孔隙率同样影响孔隙结构吸水特性。平均有效孔直径均随最大可渗孔直径、体积孔隙率的增大而增大。体积孔隙率对平均有效孔直径影响较小,孔隙率从0.15变化到0.4,平均有效孔直径仅增加了1.5倍,而最大可渗孔直径对平均有效孔直径影响显著,最大可渗孔直径从0.1 μm变化到40 μm,平均有效孔直径约增加了3个数量级。但需要注意的是,非均质性较强的孔隙结构,虽然具有大的孔隙率,但是平均有效孔直径可能较小,如图6(a)所示,这说明多孔介质自吸水力特性受孔隙微观几何特征多重因素的影响,并不是单个几何因素所能确定的。
4 平均几何与分形几何表征的模型对比分析
平均几何表征模型中的参数平均等效孔隙直径deav物理意义不甚明确,对其定量表征有一定难度,如果直接用压汞法测量的平均孔隙直径代替参数deav代入模型计算,往往计算结果偏高,分析原因可能有如下两方面:①压汞法由于汞压力的限制所得孔隙下限尺寸有限,而孔隙结构中微小孔隙数量较多,所测得平均孔隙直径可能偏大;②压汞法仅从几何空间上表征了平均孔隙直径,而孔隙结构实际水力特征尺寸还与孔隙结构的拓扑有关。
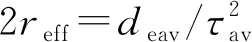
分形几何表征模型中的参数分形维数Df、最大孔隙尺寸λmax、平均迂曲度τav、体积孔隙率φV、最小孔隙尺寸与最大孔隙尺寸比值β物理意义明确,其中前三个参数可以通过X-Ray CT层析成像法借助一定的图像处理软件(如Avizo)进行精确表征,而φV可以借助MIP物理法进行精确测量,虽然λmin难于测量,但是Feng等[23]认为具有分形特征的孔隙结构比值β一般在10-2~10-4之间,可近似取β=0。一般情况下,掌握不好有效介质近似理论或二元孔隙分布理论等精确表征孔隙结构水力特征参数的方法,很难应用常规的压汞数据代入平均几何表征模型中得到准确的吸水性系数值。而分形几何表征模型可以直接应用物理法或图像法表征的平均孔隙半径与最大孔隙半径,结合分形维数对孔隙结构吸水特性加以准确描述。相比平均几何表征模型,将deav视为压汞法所测得平均孔隙直径代入所得预测结果偏大的情况,分形几何表征模型,不仅预测结果优于平均几何表征模型,而且与较为烦琐的求解模式IFU有同等精度。
另外,通过分形几何表征的模型可以间接得知,平均等效孔隙直径与孔隙结构非均质性、各向异性以及最大可渗孔隙直径、体积孔隙率有关联。对于孔隙连通以及孔吼特征较弱的孔隙介质,为获取参数deav提供了一种新方法。
5 结论与展望
(1) 本文考虑孔截面的不规则形态以及孔隙结构的迂曲特征将微观孔隙等效为毛细管束,基于H-P方程、L-Y方程、分形几何理论,经过数学推导分别获得平均几何与分形几何分别表征的修正LW吸水模型,并为间接确定描述孔隙水力特性的平均等效孔隙直径deav提供了一种新方法,一定程度上解释了其物理意义。
(2) 本模型认为表征孔隙结构吸水特性的参数S与孔隙结构几何参数(δ,τ,φ,Df,λmax)密切相关,其中参数δ、τav、Df、λmax对孔隙结构吸水特性影响较为敏感,孔隙结构吸水特性受孔隙几何多因素的影响,解释了平均孔隙空间几何尺寸较大反而吸水性较弱的原因。
(3) 平均几何表征的模型中参数deav物理意义不明确,而将有效介质理论确定的有效孔隙半径代入模型可以得到比Benavente模型更接近真实值的结果,分形几何表征的模型中各参数物理意义明确,直接可利用实测孔隙数据代入得到与实验相近的结果,相比前一种模型有其优越性。
(4) 本模型假设毛细管束单根毛细管之间是相互独立的,水分迁移过程中没有相互影响,而且毛细管沿纵向截面是统一不变的。本模型采用了均一化思想,认为各孔隙截面形状相同且迂曲度取平均值。同时,毛细管束模型中单根毛细管尺寸也相同。未来有必要针对岩石结构的非均质性、各向异性、三维拓扑等特征,构建更加精细化的孔隙结构几何模型。
