煤粒瓦斯定压吸附数学模型及数值解算

2021-06-30徐浩秦跃平毋凡刘佳褚翔宇刘晓薇

矿业科学学报 2021年4期

徐浩，秦跃平，毋凡，刘佳，褚翔宇，刘晓薇

中国矿业大学(北京) 应急管理与安全工程学院，北京 100083

掌握瓦斯在煤体中的流动规律对预测煤层气抽采产量、分析储层成藏机理和优化生产策略具有重要意义[1-2]。目前，针对煤基质中瓦斯吸附解吸的流动机理并没有统一和清楚的认识，学术界也一直对此展开了深入的研究和探讨[3-5]。

有学者认为瓦斯在煤基质中吸附解吸是受浓度差驱动的，可以用菲克扩散理论来描述。但是菲克定律中常扩散系数只能描述刚开始较短时间甲烷的扩散过程，其理论预测结果与整个解吸时间尺度上的实验值存在显著的偏差[6-9]。后续有研究人员提出了基于菲克定律的动扩散系数数学模型[10-15]，并验证了该模型可以表征气体在煤粒中的运移全过程。虽然将扩散系数变成与时间有关的函数表达式能够保持模拟和实验结果的一致性，但是它却违背了菲克定律最初设定的常扩散系数的假设条件，这可能会造成所建模型的物理意义与理论基础不明晰。另外，动扩散系数存在一些待定参数，会导致计算过程复杂化。文献[7-9，16]基于菲克和达西定律建立了在变压、定压条件下的煤粒瓦斯吸附和解吸数学模型，并通过大量的实验结果验证了数值解算结果，发现煤粒中瓦斯的流动是符合达西定律而不是菲克定律。达西定律认为瓦斯在煤粒中的流速(体积流量)与压力梯度成正比，它是基于较大尺寸孔隙内的流动。然而煤粒中存在大量的微孔隙，学者们大都认为达西定律在微孔隙中是不成立的。因此，将达西定律用来描述瓦斯在煤粒中的流动过程也受到一些争议。文献[8-9]指出煤粒的微孔隙中存在大量的吸附态瓦斯，煤粒中的瓦斯流动主要是游离瓦斯的运动。煤粒中的瓦斯无论是何种状态，其本质均可以理解为传质。

基于此，本文首先设计了定压情况下的煤粒瓦斯吸附实验。提出了瓦斯在煤粒中的流动是受游离瓦斯密度梯度驱动的理论模型，即瓦斯质量流量与游离瓦斯密度梯度成正比。之后建立了以新理论模型为基础的煤粒瓦斯定压吸附数学模型，并重新构建了基于达西定律的瓦斯吸附数学模型。通过将两种模拟解算结果与实验数据对比，直观判断所提出的理论模型是否与实验相符。详细讨论了理论模型中的关键比例系数与时间和压力的关系，旨在进一步了解煤粒中瓦斯流动的基本规律。

1 煤粒瓦斯定压吸附实验

1.1 煤样制备

煤样取自山西水峪煤矿。将从煤矿井下现场采集的煤样密封保存，运回实验室后将其置于真空烘箱中，在105 ℃下烘干2 h。之后取出煤样放入干燥器中进行冷却达到室温，再将煤样放入破碎机中破碎，并用实验筛进行筛分。根据本实验要求，最终得到的煤粒为60～80目，粒径范围为180～250 μm。实验前还需要把煤粒放入真空干燥箱中，在105 ℃的温度下干燥8 h以除去煤粒中的水分。

每组实验选取6.5 g的煤粒来测定干煤样对瓦斯气体的吸附情况。

1.2 实验系统

实验仪器采用高温高压气体吸附分析仪H-Sorb 2006，实验系统主要包括温度控制系统、等温吸附系统和数据采集系统等三部分，如图1所示。每次实验均将温度控制在35 ℃，以保证是在恒温条件下开展的煤粒瓦斯吸附实验。

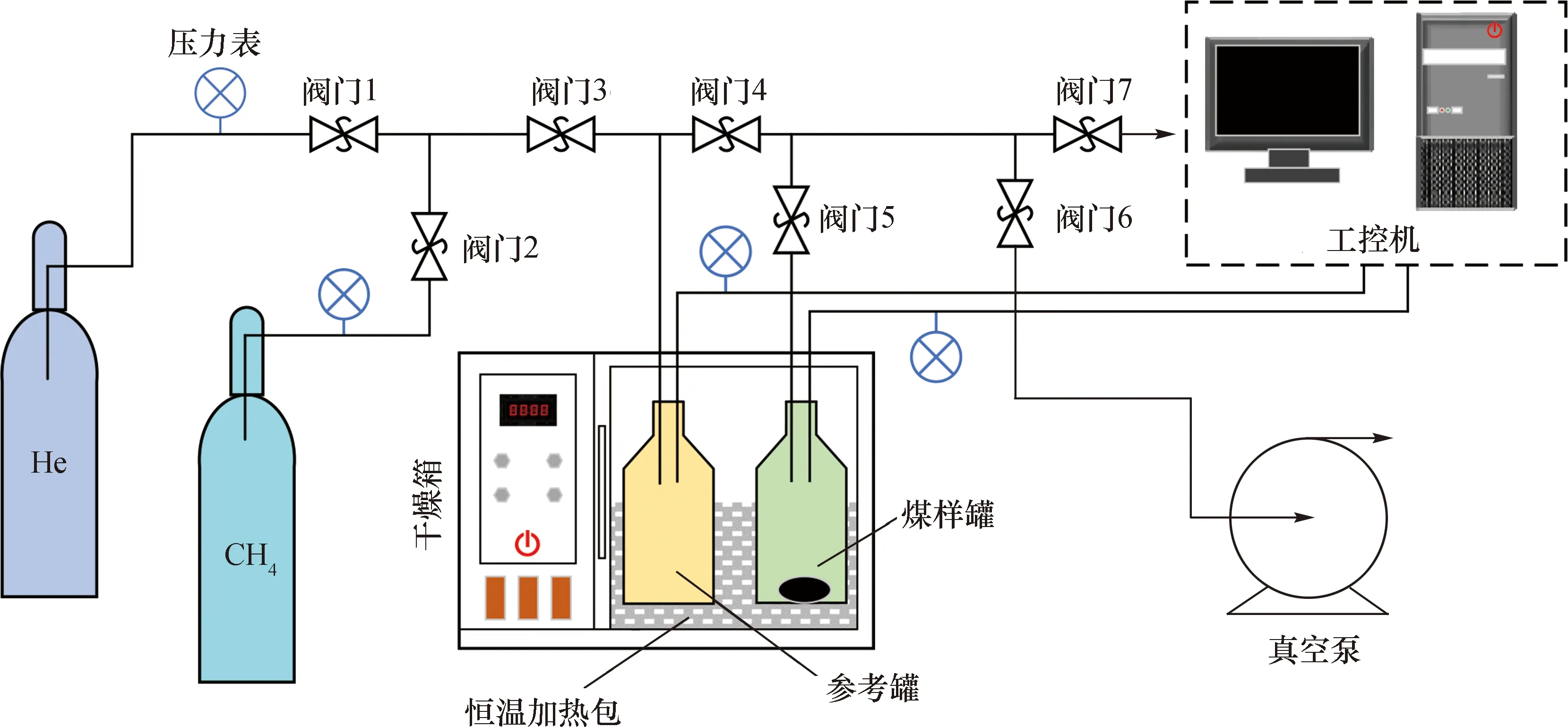
图1 实验系统

1.3 实验步骤

实验之前检测系统的气密性是否良好，必须在气密性良好的情况下开展实验，而且每组实验均需重新检测气密性以保证结果的准确性。利用真空充氦的方法测定样品罐和参考罐的实际体积，并计算出样品罐的自由空间体积。用真空泵对系统进行抽真空处理，之后向参考罐中通入瓦斯，待压力平衡后连接参考罐和样品罐。使样品罐中的煤粒在初始压力为0.5 MPa、1 MPa、2 MPa、4 MPa的4种情况下吸附瓦斯。在这过程中样品罐的压力会不断降低。为保证瓦斯在定压环境下进行吸附实验，需要不断地贯通样品罐和参考罐，使样品罐始终保持在设置的恒定压力值上，当吸附解吸平衡时实验停止；工控机的数据采集系统可以记录每秒样品罐压力的具体数值，并通过前后时间点的压差来计算样品罐中的煤粒累计瓦斯吸附量[16]。

2 达西数值模型

2.1 数学模型

文献[16]的研究结果表明，定压边界条件下煤粒中的瓦斯解吸吸附过程符合达西定律(压力梯度驱动)。本文在此基础上建立了球坐标下的煤粒瓦斯定压吸附的流动方程：

(1)

式中，a，b为朗格缪尔吸附常数，m3/t，1/MPa；ρs为煤视密度，t/m3；P为瓦斯压力p的平方，MPa2；t为吸附时间，s；A为与游离瓦斯含量有关的系数，m3/(t·MPa)；f为孔隙率；λ为瓦斯透气性系数，m2/(MPa2·d)；r为煤粒中心到其他位置的距离，m。

系数A的计算公式[17]为

(2)

式中，Tn为标准情况下的温度，K；pn为标准情况下的压力，取0.101 325 MPa；T为实验温度，K。

流动方程的初始和边界条件为

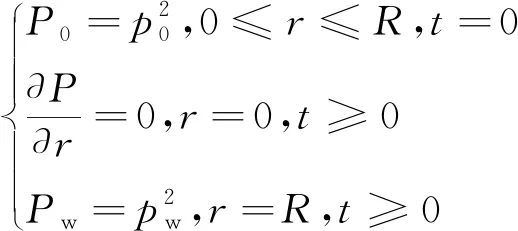
(3)

式中，p0为吸附前的煤粒中的初始压力，MPa；pw为煤粒外表面的压力，MPa；P0为初始压力的平方，MPa2；Pw为煤粒外表面压力的平方，MPa2；R为煤粒半径，m。

煤粒吸附实验前对煤粒脱气处理，所以初始时刻煤粒中的瓦斯压力约为0。与煤粒瓦斯变压吸附过程不同的是，在定压吸附实验过程中，煤粒外部空间的压力始终保持设定值。因此，煤粒外表面压力的平方Pw是不变的。

2.2 有限差分数值解算

相对于解析解，数值解可以不用设定诸多的假设，准确性也更高[18]。本文使用有限差分的数值方法求解2.1节中的数学方程[7-9]。将球形煤粒沿球的半径从球心到球表面划分为N个节点，节点间距等比变小，编号为0，1，2，3，…，N，如图2所示。

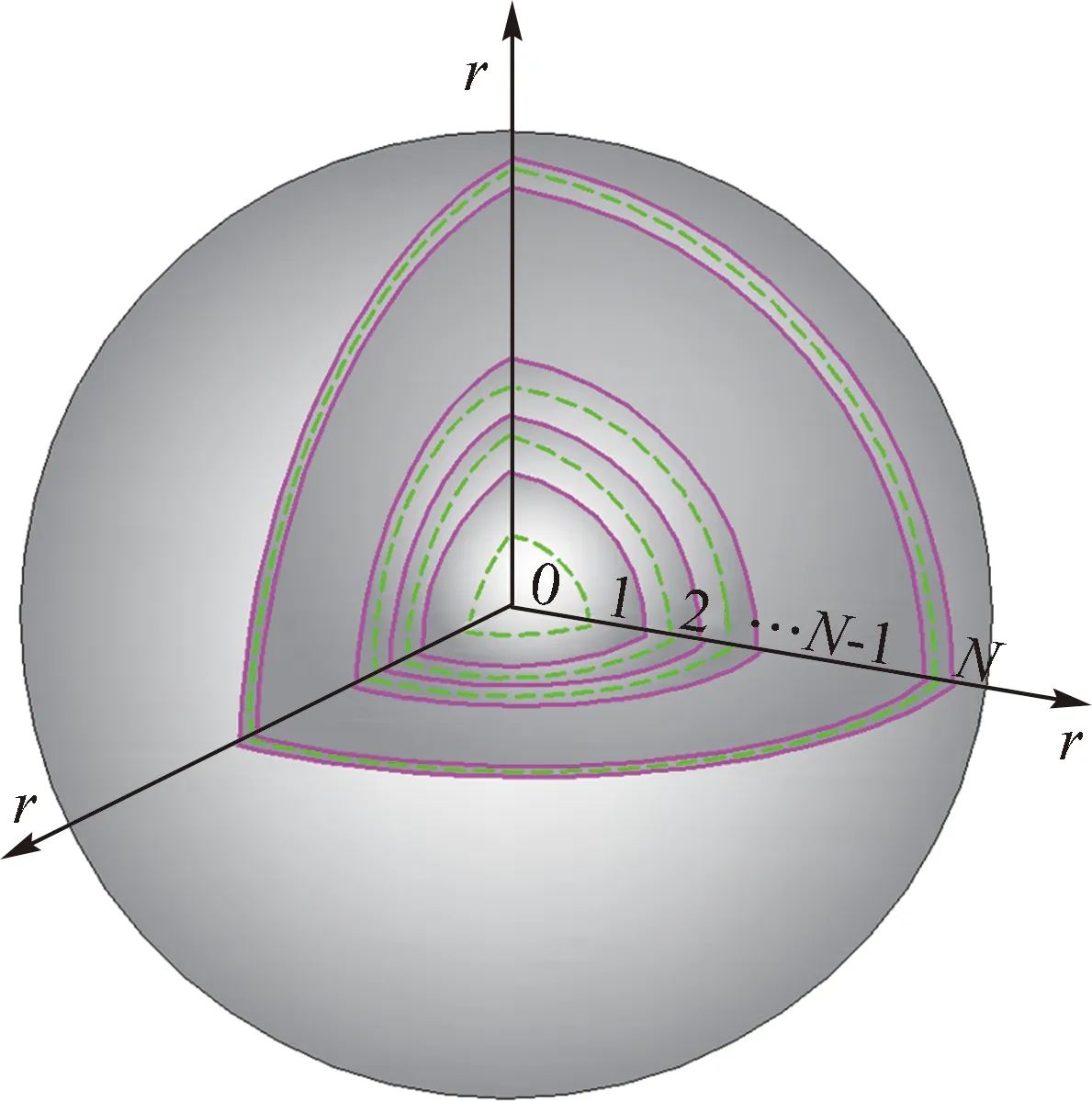
图2 球形煤粒节点划分

节点所在的球面用图2中的洋红色实线表示。以两个相邻节点间的中心作同心球面，得到绿色虚线所示的球面。相邻虚线球面之间形成球壳，而在中心处形成一个实心球体，每一个球壳或小球包含一个节点。这样可以得到以0点为中心的实心球和包含各节点的N个球壳。

根据质量守恒定律，节点1到N-1所形成的各自的球壳的非稳态瓦斯流动差分方程为

(4)

(5)

式中，i，i-1，i+1为划分节点编号；j为时间节点编号；Δtj为第j个时间步长。

节点0处的非稳态瓦斯流动的差分方程为

(6)

(7)

节点N处的非稳态瓦斯流动的差分方程为

(8)

由式(4)至式(8)构成了第j时刻以N个节点瓦斯压力为未知量的完备方程组。已知一个时间步长以及上一时刻的压力，可以计算下一时刻的压力。在此基础上，可以得到任意时间煤粒内的瓦斯压力。计算的步长采用等比步长，这样可以在保障精确度的情况下尽量节省计算时间。式(5)和式(7)的右边为第j时刻节点瓦斯压力的非线性表达式，需采用高斯迭代的方法进行求解。具体参照文献[7-9]中的解算步骤。

依据N节点和N-1节点的压力值，计算j时刻单位质量煤粒累计吸附的瓦斯体积含量：

(9)

式中，QV为单位质量煤粒累计吸附瓦斯体积，cm3/g。

3 游离瓦斯密度梯度驱动的扩散模型

3.1 数学模型

煤粒中吸附态的瓦斯数量与煤粒表面积有关；游离态的瓦斯分子能自由移动，其数量与空间有关。原始煤体中瓦斯的游离态与吸附态是处在动态平衡的环境中，一旦外部卸压，游离态的瓦斯便向外运移，而气态瓦斯的扩散与其密度梯度成正比[8]。在此基础上，提出了煤基质中瓦斯质量流量与游离瓦斯密度梯度成正比的新模型，其比例系数为瓦斯微孔道扩散系数。数学表达式如下：

(10)

式中，Jm为煤基质中瓦斯质量流量，即单位时间内通过单位面积的瓦斯质量，g/(m2·s)；Dm为微孔道游离瓦斯扩散系数，m2/s；ρg为游离态瓦斯密度，g/m3；l为等密度线外法线方向的长度，m。

游离瓦斯可视为理想气体，根据理想气体状态方程，则有

(11)

式中，p指瓦斯气体压力，MPa；Rs为通用气体常数，8.314 J/(mol·K)；M为瓦斯的摩尔质量，16 g/mol；Km为煤粒的微孔道扩散系数，g/(MPa·m·s)。

达西模型中的流动方程表示的是体积流量，而游离瓦斯密度梯度模型描述的是质量流量，则新模型下的煤粒瓦斯沿径向流动的连续方程为

(12)

式中，ρc为标准情况下的瓦斯密度，取7.17×102g/m3。

初始和边界条件为

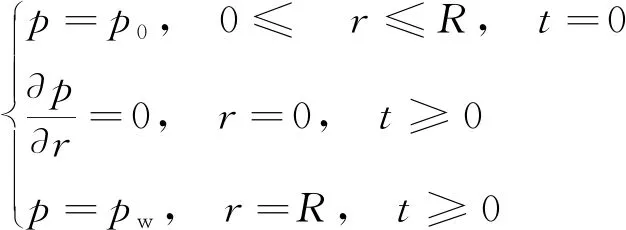
(13)

与定压吸附实验条件保持一致，煤粒内部的初始压力p0为0，外表面的压力pw始终不变。

3.2 有限差分数值解算

节点还是按照图2划分，节点1到N-1所形成的各自球壳的非稳态瓦斯流动的差分方程为

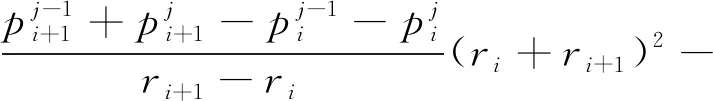
(14)

节点0所形成的各自球壳的非稳态瓦斯流动差分方程为

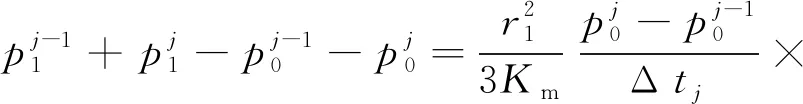
(15)

节点N所形成的各自球壳的非稳态瓦斯流动差分方程为

(16)

式(14)至式(16)构成了第j时刻以N个节点瓦斯压力为未知量的完备方程组。同样需要采用高斯迭代的方法，求解式(14)和式(15)中关于瓦斯压力的非线性表达式。基于Visual Basic程序编写相应的解算代码，程序结构流程如图3所示。

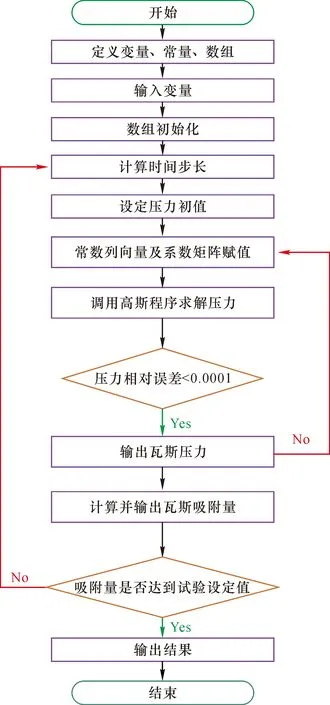
图3 程序结构流程

依据N节点和N-1节点的压力值，计算j时刻单位质量煤粒累计吸附瓦斯的质量：

(17)

式中，Qm为单位质量煤粒累计吸附瓦斯质量，g/g。

4 实验与模拟结果的对比

为了便于比较两种理论模型解算的结果，这里将基于游离瓦斯密度梯度理论模型得到的煤粒累计吸附瓦斯质量含量Qm转换为吸附体积含量QV。二者的转换关系为

(18)

数值模拟中参数的选取见表1。其中，a、b、ρs、f等均由实验手段测取，λ和Km是在解算程序中不断调试确定的。实验和模拟得到的是累计瓦斯吸附体积含量QV与时间t的变化关系。由于程序解算中的时间步长是采用等比方式，导致时间数据的波动情况太大，因此取时间(h)的对数值为横坐标，吸附量为纵坐标，分别绘制了不同初始压力情况下的曲线趋势，如图4所示。

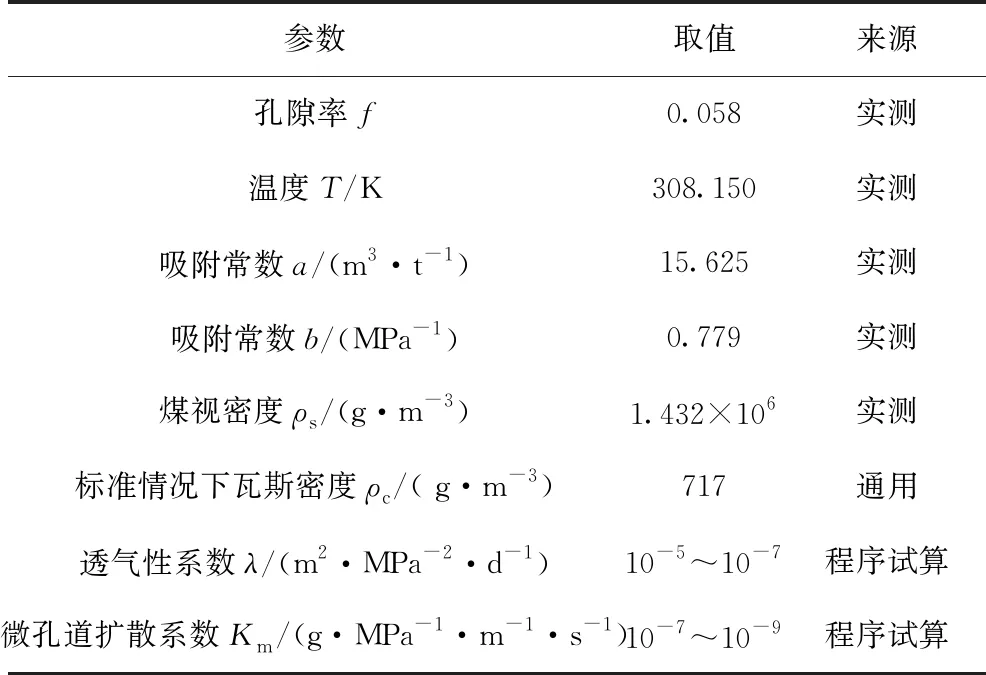
表1 模拟参数取值

由图4可以看出，在不同初始压力情况下，基于达西理论和游离瓦斯密度梯度理论模型得到的煤粒瓦斯吸附模拟结果的变化趋势，均与实验数据保持一致。由于数值模拟理想化的假设条件，导致一些模拟数值点和实验点存在些许误差，但从整体上来看也是可以接受的。这在一定程度上说明新提出来的理论模型能够用来描述煤粒瓦斯的流动过程。另外，通过模拟结果和实验数据进行匹配，可反演出两种关键系数(λ和Km)的具体值，它们随压力的变化关系如图5所示。

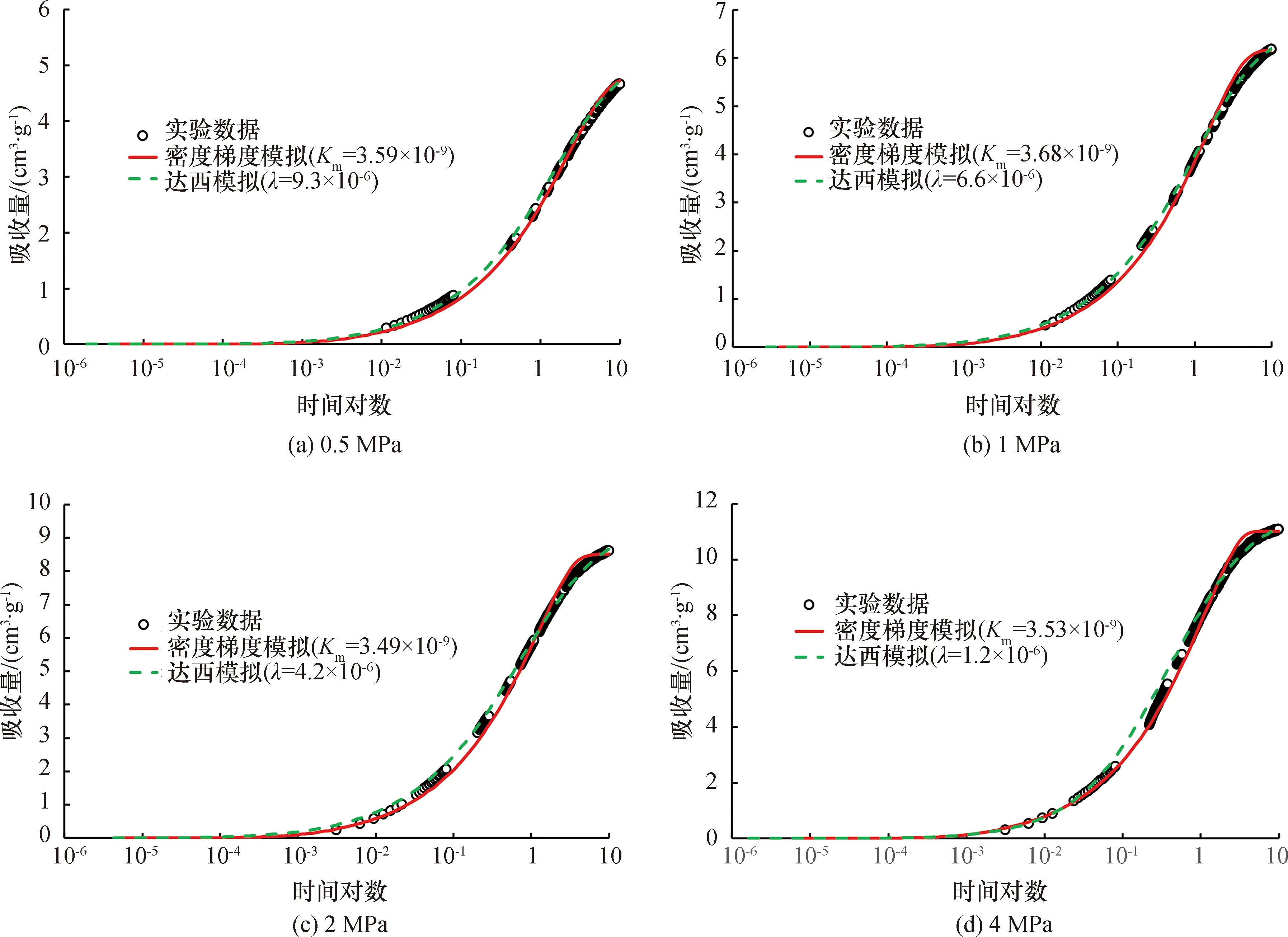
图4 模拟与实验结果对比

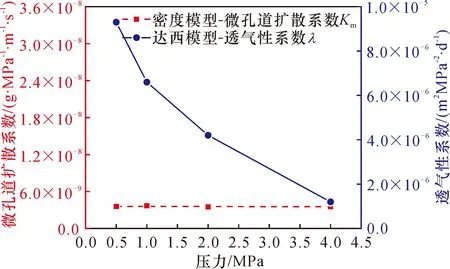
图5 关键系数随压力变化趋势

由图4可以看出，λ和Km均不随时间的变化而改变；图5则显示出λ随初始压力的增大而减小，且变化幅度较大，从0.5 MPa到4 MPa透气性系数下降了将近8倍；而Km在不同压力情况下几乎保持不变，微孔道扩散系数受压力影响很小。众所周知，从理论上计算瓦斯抽采量时，需要清楚地认识到瓦斯在煤基质中的流动规律。要保证计算结果的准确性，达西模型中的透气性系数必须随压力的增大而减小，而本文新提出的游离瓦斯密度梯度理论模型中的微孔道扩散系数则不受此限制。通常，开采煤层中各处的瓦斯压力分布不均匀，且受扰动的影响不断变化，此种情况下新假说的优势显而易见。

5 讨论

学术界针对瓦斯在煤粒中的运输机制还没有统一的认识，大都认为煤粒中的瓦斯流动符合菲克扩散定律(浓度梯度驱动)[19-21]。本课题组也对此作了深入研究，发现基于菲克定律的瓦斯流动模型所预测的结果与实验值存在明显的偏差，只有当菲克定律的扩散系数随时间不断减小时才能与实验结果相吻合[7-9，22-23]。之后经过变压、定压下的煤粒瓦斯吸附和解吸等多种条件下的大量实验证明：基于达西定律(压力梯度驱动)建立数值模型的模拟结果与实验数据相一致，其中的透气性系数是不随时间变化的，因此认为瓦斯在煤粒中的流动机理服从达西定律而不是菲克定律。

然而后续的研究中却发现，在不同初始压力条件下，根据实验数据反演出的煤粒透气性系数却出现很大的差别，透气性系数与试验初始压力近似成反比关系[23]。但实际上，如果菲克和达西理论模型是正确的，则其中的关键比例系数不应随时间或压力的变化而变化。故而无论是菲克定律还是达西定律都不能很好地描述煤粒中的瓦斯流动过程。根据达西定律只能推出瓦斯的体积流量与压力梯度成正比，而不是质量流量(单位时间单位面积上通过的瓦斯质量)与压力梯度成正比，这可能是在不同压力条件下透气性系数出现巨大差异的根本原因。

本文提出的煤粒中瓦斯质量流量与游离瓦斯密度梯度成正比的新理论模型得到了较好的验证。通过将模拟结果与实验数据匹配可知，其中的关键比例系数(微孔道扩散系数)与压力、时间等参数无关。