浅谈初中数学解应用题中的“列式”技巧

邹显慧

摘 要：应用题的教学是激发学生学习兴趣，提高学生数学应用意识，培养学生学数学、用数学的很好手段和途径。因此，应用题教学的目标分为两个阶段：第一阶段是能够从具体问题中找出数量关系并用数学的方式表示数量关系;第二阶段是解数学问题并能验证所得结论是否符合数学意义和生活意义。其中第一阶段是应用题教学的核心，也是应用题教学的重点和难点，有效突破第一阶段的教学才能让应用题列式问题迎刃而解。

关键词：初中数学;解应用题;列式技巧

利用数学知识解决实际问题是中考重点之一，不仅有填空题、选择题和解答题，而且覆盖代数、几何等各类题型。如何从繁杂的条件中找到等量或不等量关系，一直是教师教学中的难点。因此，我们在教学中可以尝试用以下三种技巧来解决“列式”难题。

一、直译法

“直译法”就是根据题目中含有“比”和“是”的语句，直接翻译成数学的符号语言，形成方程或不等式。

例：到2011年底，我国风力发电机容量为4500万千瓦，比2005年底的43倍还多6.5万千瓦。求2010年底我国风力发电装机容量是多少？

分析：设2005年底我国风力发电装机容量为x万千瓦，“比”→“=”，“倍”→“多”→“+”，“4500万千瓦比2010年底的43倍还多6.5万千瓦”→“4500=x×43+6.5”

直译法来源于题目条件，不需要学生走弯路就能轻松列式。因此一定要注重让学生找出题目中“比”“是”“多”“小”“倍”“不超过”这样的关键词。

二、转化法

应用题文字一般较多，学生在读题中会存在审题不清的问题，“转化法”是帮助学生寻找“数量关系”的一种方法和手段，在代数应用题中基本步骤为：逐句阅读寻找数字条件;结合实际明确生活含义，用简单文字和数学符号表示存在关系;设出未知字母或运用题中变量字母，并用字母取代简化式中有关文字;确定数量关系式，判断数量关系的合理性和准确性。

例：某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台，电视机进价2000元/台，售价2100元/台;冰箱每台进价2400元/台，售价2500元/台;洗衣机进价1600元/台，售价1700元/台。在不超出现有资金的前提下，若购进电视机的数量和冰箱的数量相同，洗衣机数量不大于电视机数量的一半，商场有哪几种进货方案？

分析：第一步“简化”：①32400元→不超过这么多钱的前提下，买三种商品→数量关系：电视机费+电冰箱费+洗衣机费≤32400;②15台→意义：三种商品的总数量→数量关系：电视机数+电冰箱数+洗衣机数=15;③电视机的数量和冰箱的数量相同→电视机数=电冰箱数;④洗衣机的数量不大于电视机数量的一半→洗衣机数≤0.5电冰箱数;⑤数量关系→购买商品总费用=商品的进价×商品的数量。

第二步“转化”：由③④都包含电视机数量可设电视机的数量为x台，将x分别取代②③中“电视机的数量”，则可得出：冰箱的数量为x台，洗衣机的数量为（15-2x）台。再将字母取代④中文字可得数学关系：15-2x≤0.5x，结合①⑤用字母取代文字可得：2000x+2400x+1600（15-2x）≤32400，分别解这两个不等式问题即可解决。

此种方法不用过多思考，按程序进行简化、转化就能达到目标。特别要注意的是所有应用题中存在着的生活中的等量关系应首先写明。

三、表格法

“表格法”第一步：找一个等量关系设元，另一个等量关系来列式。第二步：设计表型。问题中通常涉及两者之间的各种数量的比较，如“骑自行车与乘汽车”“原计划与实际”等。列表时表格横向表示数量，纵向表示两个对象。第三步：填表。边读题边将已知量填入表中，再填数量关系，最后填未知量及含未知量的代数式，填过后一定会有一个等量关系供列方程或不等式使用。

例：某校九年级学生由距景点10千米的学校出发前往参观，一部分同学骑自行车先走，过了20分钟后，其余同学乘汽车出发，结果他们同时到达，已知汽车的速度是骑自行车同学速度的2倍，求骑车同学的速度。

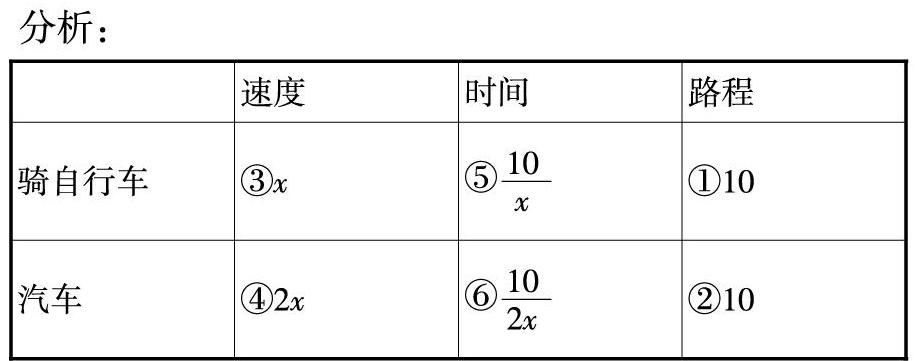
分析：

由骑自行车和乘汽車所走的路程相同都为10千米填得①②，设骑自行车同学的速度为x千米/时填得③，由汽车速度是骑自行车同学速度的3倍填得④，根据基本公式：时间=路程÷速度填得⑤⑥，最后根据骑自行车的同学先出发20分钟，乘汽车的同学出发，结果同时到达可列方程。

可以看得出，用列表法解应用题可以分散难点，表格中不仅能容纳所有数量关系，且容易填写，易于学生掌握和运用。列表法降低了问题的难度，激发了学生的解题兴趣，做到了良性循环，从根本上解决了学生对解方程应用题的顾虑。

代数应用题的特点是文字语言叙述比较多，生活信息量大，学生在阅读的过程中容易受到生活中概念因素的影响，给学生“列式”造成障碍，运用以上技巧，则可以帮学生更清楚地列出方程或不等式，规范学生正确的数学思维过程，进而提高学生解决应用题的能力。以上只是应用题教学中“列式”的一些手段和方式。实际应用时要根据具体情况，把以上方法有机结合起来，合理选择、灵活运用会更好提高效率，取得成绩。

参考文献：

[1]苏小霞.初中数学应用题教学策略研究[D].兰州：西北师范大学，2009.

[2]马侃.初中应用题“懂而不会”现象的原因分析与对策研究[D].济南：山东师范大学，2014.