一种半主动自参数吸振器的设计与分析研究*

田 缀

（西安电子科技大学，陕西西安710071）

引 言

无论是生产中还是生活中，振动都是一种常见的现象。随着机械设备运行速度的提高，相关的振动问题越来越受到人们的关注。振动不仅容易引起结构的疲劳损伤，加速机器老化，影响设备寿命，而且还会降低仪器仪表的测量精度。除此之外，针对敏感设备面临的日益苛刻的振动环境适应性要求，开展减振设计方法和应用研究成为无法规避、必须解决的关键技术之一[1]。

国内外学者对机载电子设备的减振设计方法进行了大量的研究。长期以来，结构振动控制的发展很多都局限于线性振动控制的研究。通常，对机载设备进行减振一般有如下几种方法：1）从优化设备结构形式上进行减振设计[2–3]；2）通过安装阻尼器、涂覆阻尼材料等措施增加系统阻尼来减小系统振动响应[4]；3）安装吸振器将电子设备的振动响应转移到吸振器的振子上[5]。其中安装吸振器的方式具有实施简单、减振效果明显的优点，受到大量设计师的青睐，特别是在机载电子设备领域应用最为广泛。

然而，随着科学技术的不断进步，仅用线性理论分析非线性系统的动力学行为还显得很不够，在某些特定情况下，非光滑和不连续因素对机械工程问题的影响越来越引起人们的关注，考虑系统中非线性因素对系统动力学行为的影响已成为非线性动力学研究的热点之一[6]，应用非线性吸振器进行振动能量的衰减和吸收也开始引起学者们的兴趣[7–8]。非线性吸振器具有多种吸振原理，如非线性能量阱、自参数共振等。自参数吸振器（Auto-parametric Vibration Absorber,AVA）是较为常见的一种非线性吸振器。在工程应用中，为了减小主系统的振动，通常给主系统增加一个摆或类似摆作用的辅助机构[9]，而把原先的振动系统转变为自参数振动系统。由于自参数共振产生内作用而使摆开始摆动，吸收主系统的部分能量，从而减弱主系统的振动。自参数动力吸振器就是利用该原理制成。

众所周知，线性动力吸振器（Tuned Mass Damper,TMD）是机械结构中常用的线性动力吸振器，在工程中得到了广泛的应用，对其加入主动控制策略从而引入了主动TMD、半主动TMD和混合TMD的概念，可以实现对结构振动更好的减振效果以及鲁棒性。而自参数吸振器是一种典型的非线性吸振器，尤其适用于机械结构的非线性振动控制，其减振效果已经被很多学者证实[10]。除此之外，为了扩大自参数单摆的有效带宽，文献[11]还研究了一系列固有频率略有不同的单摆。然而，如果采取被动控制的方式抑制结构振动，吸振器一旦设计制作完成，将不能适应系统、环境等不断改变的要求，其性能将发生改变[12–13]。这些因素均会使得被动装置结构振动控制的鲁棒性不尽如人意，而半主动控制可以解决这一问题，尤其适用于中等振幅和大振幅。本文以单摆自参数吸振器为研究对象，详细研究了其解的形式以及半平凡解的稳定性，通过对单摆摆长的主动控制，提出了时变摆长的概念，对半主动单摆自参数吸振器进行研究设计。最后利用数值仿真的方法验证了半主动自参数吸振器较好的减振效果。

1 单摆自参数吸振器

考虑一个带有粘性阻尼摆的自参数动力吸振器的自参数耦合动力系统（图1）。其中，t为时间；m1,c1,k1为线性主结构的质量、阻尼和刚度系数；m2,c2为摆的质量和阻尼系数；l为其摆长；x为主结构在外力Fcos(ωt)作用下的垂直振动响应；ω为激励频率；θ为非线性耦合项ml¨xsinθ对单摆自参数吸振器进行参数激励而产生的摆幅。

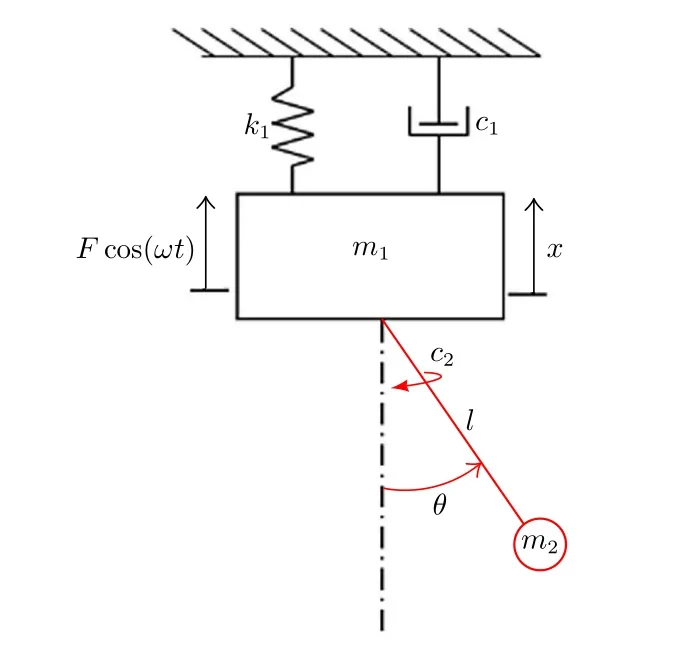
图1 带有单摆自参数吸振器的主结构

根据Hamilton原理，该耦合系统的控制方程为：

利用表1定义的符号，式（1）的控制方程可以转换为无量纲形式：

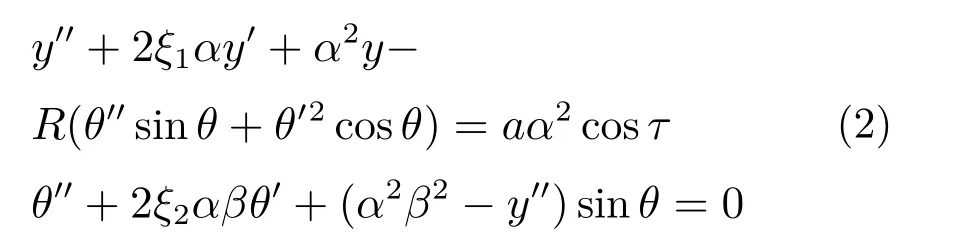
表1 文中的无量纲符号定义

1.1 半平凡解与非平凡解

本文讨论由外力引起的自参数耦合系统的谐波运动。通常情况下，有两种解。一种是半平凡解，即单摆不摆动，主结构受外力激励而进行谐波振动。即：

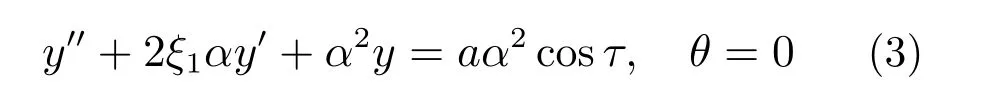
主系统的响应幅值A0可表示为：

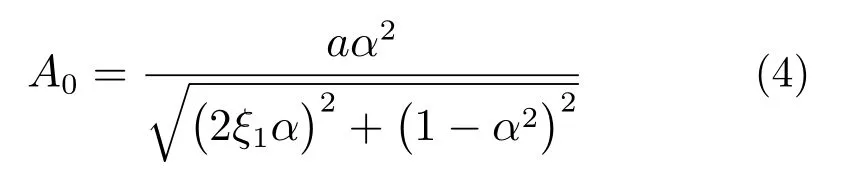
另一种是非平凡解。单摆AVA平衡位置由于2:1的内共振而变得不稳定，从而引起单摆的摆动，进而导致主结构的振动减小。这时，施加在主结构上的力不仅包括外激励，还包括由于单摆AVA的振动而产生的反作用力。假设耦合系统的非平凡解为：

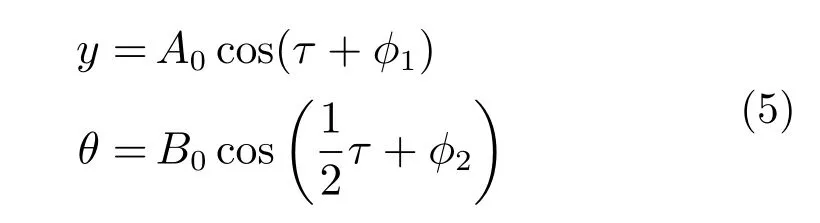
式中：ϕ1,ϕ2分别为响应y,θ的相位差；B0为响应θ的幅值。将式（5）代入式（2），主系统的响应幅值A0可表示为[9]：

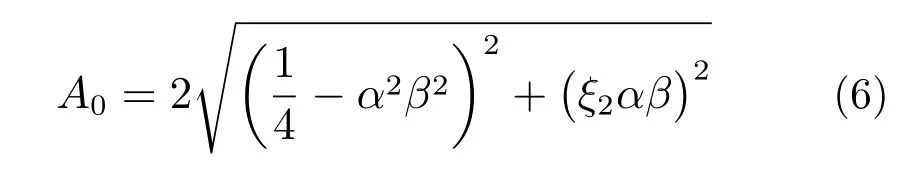
由式（6）可以看出，当αβ=1/2（ω2/ω=1/2）时，A0可以得到最小的响应。此外，和线性TMD相似，单摆AVA的减振效果主要取决于自身参数的合理设计。本文主要利用变刚度的方法使主结构在耦合系统自参数共振区域[ωa,ωb]的响应A0最小，即在定义为[ωa,ωb]的自参数共振区域中一直有ω2/ω≈1/2。因此，为了减小主结构的振动响应，应首先得到式（2）中耦合系统的非平凡解。

1.2 半平凡解稳定边界

自参数耦合系统半平凡解和非平凡解之间的稳定边界的寻找最终归结于经典的Mathieu方程的稳定性边界研究。假设ε为无穷小量，Mathieu方程是最简单的具有参数不稳定性的方程，其中有无穷多个频率是不稳定的，而最不稳定的是第一次谐波频率：

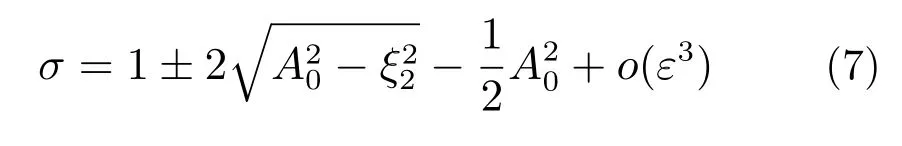
图2给出了不同阻尼比下非线性耦合系统第一次谐波频率的稳定边界。不稳定区域为非半平凡解的频率区域。可以看到：随着阻尼比的增大，不稳定区域有缩小的趋势。也就是说，对于较小的阻尼比，半平凡解更容易变得不稳定，单摆吸振器也更容易被激励，从而吸收主结构的振动能量。

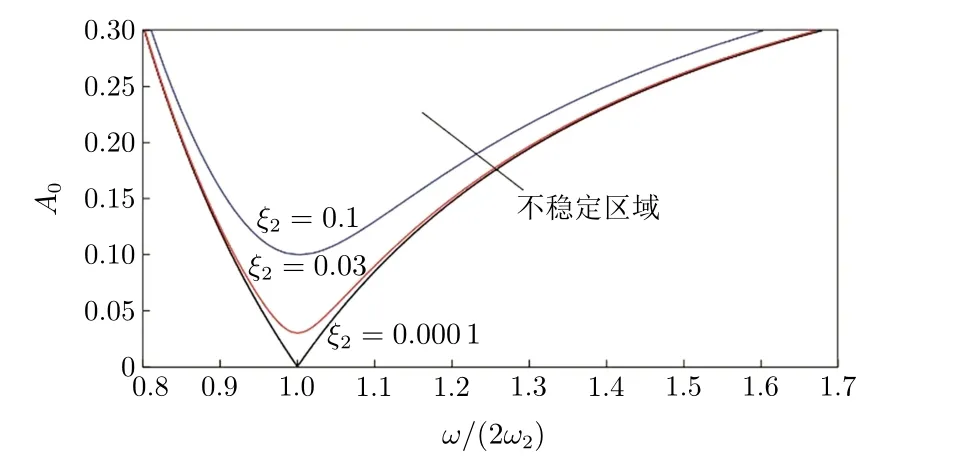
图2 自参数系统半平凡解的稳定边界

随着自参数激励幅值A0的增大，次谐波频率附近的不稳定区域呈不对称趋势。在不稳定区域的非对称区域，文献[14]发现存在两个非平凡解的Hopf分岔，唯一的非平凡解将失去稳定性。因此，为了避免非平凡解的进一步不稳定，进而发生混沌现象，本文研究在小幅激励下的半主动自参数吸振器的减振性能。

2 半主动单摆自参数吸振器

半主动单摆自参数吸振器的实现主要是通过向单摆增加控制，进而根据外界激励频率来主动控制单摆的固有频率，使主结构在自参数共振区域响应最低点处相应的αβ始终等于或接近1/2。

2.1 半主动自参数单摆数值建模

为了用相应的精确αβ来跟踪最低点，用不同的频率比β计算了一系列的幅值响应曲线，然后确定每个幅值响应曲线对应的最低点（对应的α）。图3显示了在每个最低点选择的α和β的值，并给出了α与β的线性拟合曲线。可以看出，在小激励幅度下与解αβ=1/2的拟合曲线吻合较好。

使用图3自参数共振区中的精确值进行计算，图4是主结构和分别带有被动和半主动单摆自参数吸振器的主结构的频响曲线。可以看出：与被动自参数吸振器相比，半主动方法改善了单摆自参数吸振器的阻尼效果，增大了耦合系统的自参数共振区域（有效带宽）。图5是单摆的相应频响曲线，表明了主结构和被动、半主动自参数吸振器的自参数共振区域[ωa,ωb]。值得一提的是：在自参数共振区域[ωa,ωb]内，单摆的频率随激励频率而变化；而在该区域之外，摆的频率是固定的，频率比β设定为0.5。

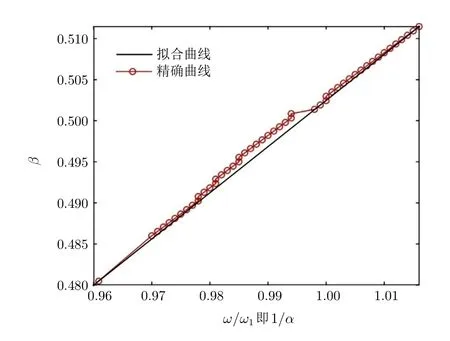
图3 在幅值响应最低点的α和β的关系图

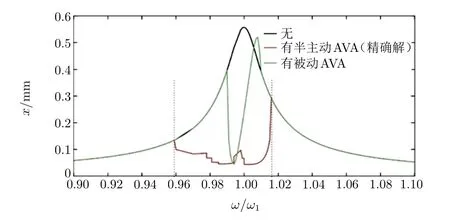
图4 主结构和主结构带有被动、半主动单摆AVA的频响曲线（精确值见图3 ）

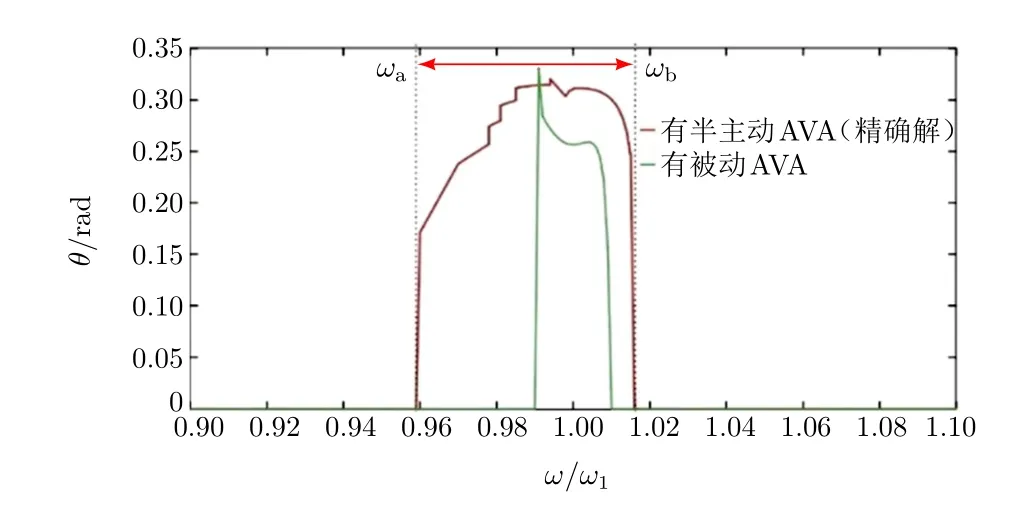
图5 被动和半主动单摆AVA的频响曲线

图6和图7将利用自参数共振区域中的精确值和拟合值计算得到的半主动自参数吸振器的减振效果进行了比较。可以看出：在耦合系统自参数共振区域[ωa,ωb]，依据ω2/ω=1/2，半主动单摆自参数吸振器在工程中可以线性实现。

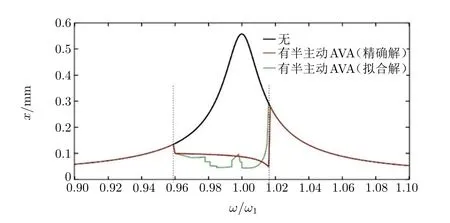
图6 主结构和主结构带有半主动单摆AVA的频响曲线

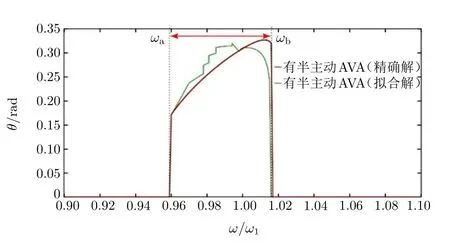
图7 半主动单摆AVA的频响曲线（精确值和拟合值见图3 ）

2.2 时变摆长设计

众所周知，单摆的固有频率可以很简单地根据其长度来调整。因此，在一定的扫频速度下，本文设计了一个单摆长度随扫频激励频率ω变化的半主动自参数吸振器。单摆长度可以根据每个频响曲线的最低点αβ的值来调整，其变化规律如下：

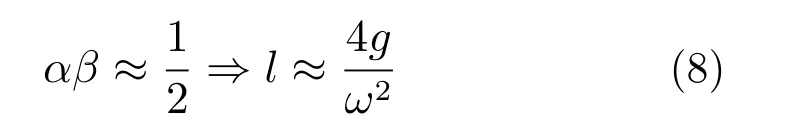
图8是式（8）中的扫频激励频率与单摆长度之间的关系图。摆长随激励频率的增加呈抛物线型变化。可以看出：基于分段线性化方法，可以在自参数共振区域[ωa,ωb]进行线性化处理，因此可以得到一个便于工程应用的时变摆长的半主动自参数吸振器。

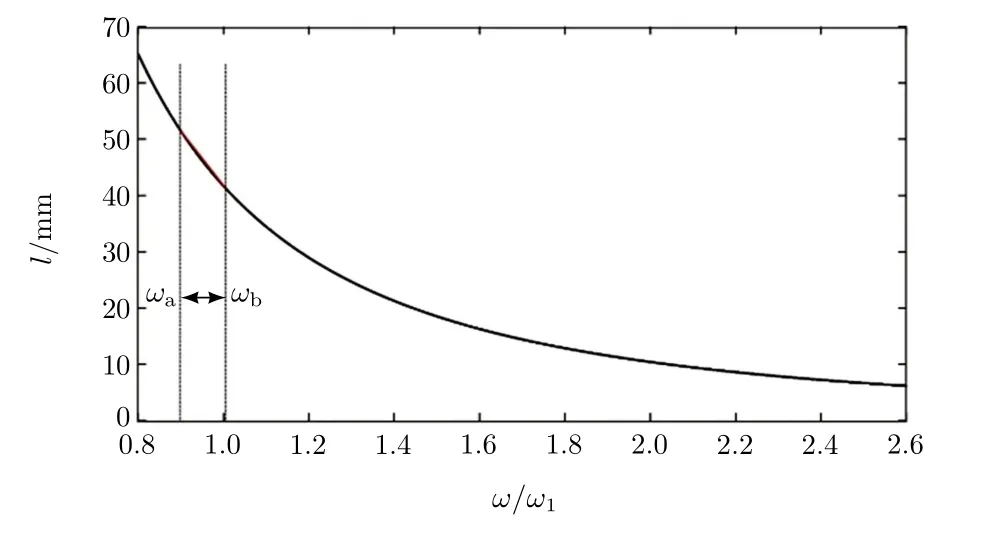
图8 摆长与激励频率的变化规律

然而，在工程应用中，实现时变长度是一个有待解决的问题。一方面，可以使用带有记忆元件的智能材料来实现。例如，形状记忆合金允许从温度变化引起的相变中恢复高达5%的应变[15]。摆的时变长度应通过在线识别信号进行动态补偿[16]。另一方面，如果将由永磁体组成的刚度调节装置连接到单摆上，可以根据所产生的磁力直接调节单摆的固有频率[17]。

3 数值仿真

利用Simulink对图1的自参数耦合系统进行仿真分析，其主结构有量纲参数为：ξ0=1%，Ω=4.8 Hz，m1=5 kg。在工程应用中，为了不改变主结构的动力学行为，被动TMD的质量通常为主结构的1%∼3%。对于自参数吸振器的被动装置也同样如此。假设单摆自参数吸振器的质量为主结构的3%，激励振幅为0.35 N，为了便于得到自参数吸振器的非平凡解，将其单摆阻尼比设定为0.1%，接近于零。给单摆施加主动控制后，单摆自参数吸振器的减振性能可通过其长度来调节。单摆摆长通过扫频速度进行线性调节。

图9是带有被动和半主动单摆自参数吸振器的主结构的频响曲线。可以看出：在线性扫频激励下，采用半主动方式提高了被动单摆自参数吸振器的减振性能。需要注意的是，当单摆自参数吸振器在自参数共振区域内振动时，由于其非线性效应，主结构的频响曲线会出现微小的振荡现象。此外，在恒定扫描速度0.03 Hz⁄s下，在自动参数共振区域内的单摆长度可从48 mm线性变化到39 mm。

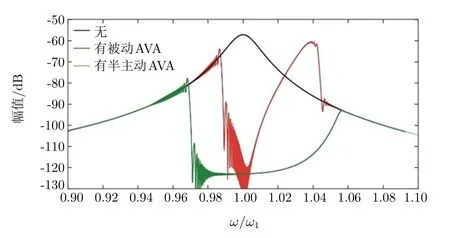
图9 带有被动AVA和半主动AVA的主结构的频响曲线

4 结束语

本文提出了一种半主动自参数吸振器的数值设计方法；通过对带有吸振器的线性主结构的自参数耦合系统半平凡解稳定性边界的探讨，找出了在自参数共振区域半主动单摆自参数吸振器频率的线性变化规律；进而基于分段线性化方法，提出了便于工程应用的时变摆长的设计方法。数值仿真结果表明：在相同质量的条件下，半主动单摆自参数吸振器很好地改善了被动自参数吸振器的减振性能。受目前条件所限，不能对该半主动单摆自参数吸振器进行试验验证，仅用数值仿真的办法对其有效性进行了验证。关于半主动单摆自参数吸振器的实验模型的建立及其减振效果的实验验证，将是后续工作中的研究重点。