一道抛物线切线问题的多种解法赏析

四川省德阳中学校 李代辉

笔者在实际教学中发现涉及直线与抛物线相切问题时，同学们的得分都很低，究其原因在于思路不明晰，无处下手。下面我以一道例题为例，介绍涉及直线与抛物线相切问题的解题思路。

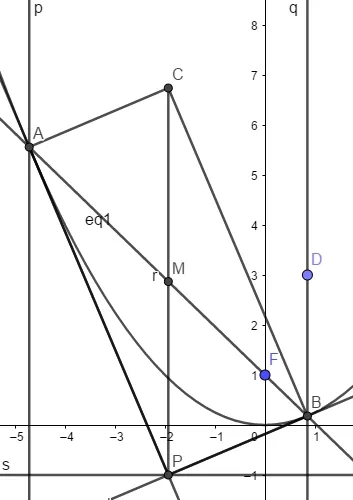
例题：已知抛物线C：x2=4y，AB为过焦点F的弦，过A，B分别作抛物线的切线，两切线交于点P，设A（x1，y1），B（x2，y2），P（x0，y0），则下列结论正确的有_（试题来源：西昌市2020学年高二上期半期试卷16题）。

①若直线AB的斜率为-1，则弦|AB|=8；

②若直线AB的斜率为-1，则x0=2；

③点P恒在平行于x轴的直线y=-1上；

④若点M（xM，yM）是弦AB的中点，则xM=x0

思路分析一：由题意，需要找2条切线的交点，所以关键要找出切线来，由抛物线上两点出发找切线是一个不错的思路。

总结：当切线不定时，两种方法都是假设切点，求出切线斜率，得到切线。

思路分析三：由抛物线光学性质，经过焦点的直线经抛物线反射后得一组平行于对称轴的直线，反射面就是过反射点处的抛物线上的切线，利用这一性质结合几何图形求解。

由以上解法可知，涉及直线与抛物线相切问题时，找出切线是一个常见思路，而从几何出发，结合抛物线的光学性质也不错。