数列常考题型及破题思路

扬州大学附属中学东部分校 高 燕

对学生来说，数列在高中数学学习中是一个重点，也是学生在进入大学后学习高数的基础知识，所以高考对于数列的考查每年都不会遗漏，而且往往会考得比较全面，将等比数列、等差数列和很多方面的知识相联系，形成考核学生知识体系的综合题型。命题往往从三个方面进行，第一个方面是数列本身的相关知识，比如等比数列和等差数列的求和、概念、性质、通项公式等，这类题目言简意赅，考查学生对数列公式的灵活运用；第二个方面是数列和函数、不等式、三角、几何等知识的结合，这类题目主要考查学生对知识的综合应用能力和灵活变换能力；第三个方面是数列的应用问题，这类题目与实际生活中的问题相结合，考查学生对题目的理解是否到位，是否能用学过的数列知识来解决实际问题，有助于提高学生分析问题和解决问题的能力。三类题目归根到底考查的都是学生对数列知识的整合应用，学生首先要夯实基础知识，熟练掌握等差数列和等比数列的定义、性质、通项公式、前n项和公式等基础知识，然后了解数列的常考题型，在做题过程中系统掌握解题的思路，勤加练习之后就可以对数列常考问题做到得心应手。教师在平时的教学中要促进学生系统掌握基础知识、基本技能、基本方法，善于培养学生综合运用数学思想方法分析问题与解决问题的能力。本文详细介绍了数列知识的常考题型和解决思路。

一、等比数列、等差数列的基本量问题

等比数列和等差数列中一共有五个基本量：a1，an，d（q），n，Sn，五个基本量我们可以做到“知三求二”，也就是只要知道其中三个，就可以通过列方程或者方程组把另外两个量求出来。解答这类问题时，首先明确已知基本量、确定量和量之间的关系，根据题目意思列出相应方程或者方程组，同时还要灵活应用等比数列和等差数列的性质，可以在一定程度上降低计算量，从而更快速地解答问题。

例1：记Sn为数列{an}的前n项和，若a4+a5=24，S6=48，则{an}的公差为（ ）

A. 1 B. 2 C. 4 D. 8

二、求数列通项及前n项和

求数列通项及前n项和的问题是数列中的一个考查重点，而且经常出现在大题中，难度跨越很大，常见的几种方法是利用数列的定义求通项公式、已知递推公式求通项公式、利用an与Sn的关系来求通项。详细举例如下：

1.观察归纳法或公式法求通项和前n项和

有的看起来较为复杂的数列，如果已知一个数列的某几项，可以通过计算出前面几项来猜想出规律，之后用数学归纳法或者反推法来进行证明，这种题目有时难度较大。有时已知数列，需要用公式法来求通项，这就需要牢记等差数列的通项公式：an=a1+(n-1)d以及等比数列的通项公式an=a1·qn-1。

常用的求和方法有以下几种：公式法求和，倒序相加法，错位相减法，裂项相消法，分组求和法。

这道题就是求数列通项和前n项和的经典题型，第一问中，利用数列{an}的前n项和an与Sn的关系，根据题意列出方程组，求解该方程组得到一个关于an和an+1的方程，从而得到an和an+1的关系，即求出公差d。第二问中，首先观察Tn的表达式，表示出Tn的前几项后可以观察出Tn为“差比数列”，这就是典型的首选错位相减法的类型，从而求出Tn。需要注意的是，错位相减后，等比数列的次数不能搞错，计算过程中要细心。

2.已知递推公式求通项公式

已知数列的递推关系，需要先识别是哪种形式的递推关系，记住以下几种常见的递推公式，然后选择相应方法进行解决：

①an+1=an+f（n），一般使用累加法；

②an+1=an×f（n），一般使用累乘法或者构造法；

③an+1=p×an+f（n），一般使用构造法（p为常数且不等于1）。

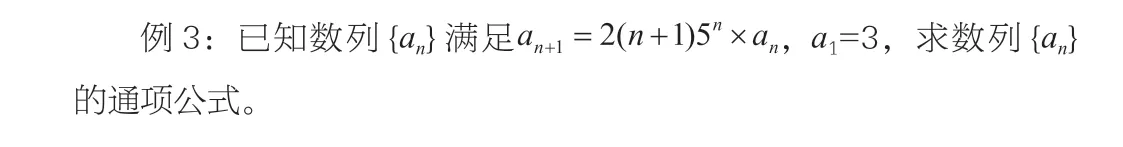
分析：看到题目所给条件，是已知an+1和an的递推公式，并且是形如an+1=an×f（n），所以想到用累乘法，将an转化为

3.利用an与Sn的关系来求通项公式

三、数列与函数的综合问题

数列和函数、不等式、三角、几何等知识的结合是一种常考题型，其中最常见的是数列与函数的综合问题。以数列为背景求函数的解析式或者用函数解析式表示出数列的递推关系，然后求数列的通项以及前n项和，用数列表示函数性质，从而求函数的单调性和最值等。

例4：等差数列{an}中，设Sn为其前n项和，且a1＞0，S3=S11，当n为多少时，Sn最大？

分析：这是一道考查数列极值的问题，较为简单，利用数列中Sn与n的关系构造一个二次函数关系式，根据这个二次函数的性质求出Sn的表达式，从而得到Sn的最大值。

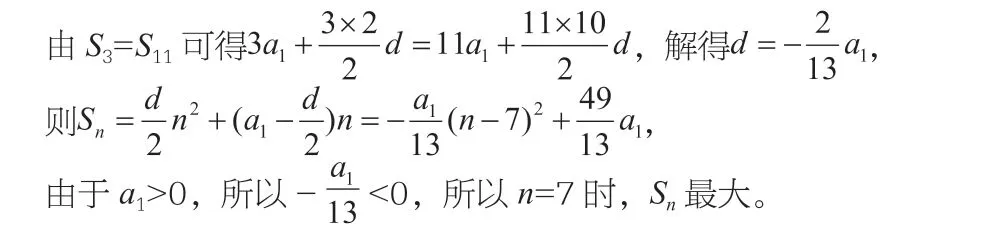
其他常见题型还有数列与不等式的综合题型，比如判断数列中的一些不等关系、项与项之间的大小、不等式的恒成立问题等。与数列相关的不等式的证明题往往难度较大，需要灵活选择证明方法。

四、数列的应用问题

生活中的很多实际问题都与数列有关，比如银行存款的利率问题、数学史与数列结合等，数列的应用问题往往伴随大量的文字叙述，在拿到题目时，首先要做到不能被大段的文字吓到，而是要仔细阅读题目，在正确理解题意的基础上，从中抽取出数学模型，将应用问题转化为数列相关的数学问题，将复杂、不熟悉的事物转化为已知、熟悉的，从而用常见的数列解决方法来得到正确解答。这类题目有利于学生形成规范化的思考，提高解决实际问题的能力。

例5：某人从2004年初向银行申请个人住房公积金贷款20万元用于购房，贷款的月利率为3.375%，并按复利计算，每月等额还贷一次，并从贷款后的次月开始归还。如果10年还清，那么每月应还贷多少元？对于分期付款，银行有如下的规定：（1）分期付款按复利计息，每期所付款额相同，且在期末付款；（2）到最后一次付款时，各期所付的款额的本利和等于商品售价的本利和。

分析：设每月应还贷x元，付款次数为120次，则x[1+（1+3.375%）+（1+3.375%）2+…+（1+3.375%）119]= 200000×（1+3.375%）120。

由此解出x≈2029.66，所以每月应还贷2029.66元。

这道题目是关于银行利率的问题，题目叙述有点长，但是只要仔细阅读题目，就可以将这个问题简化为一个等比数列求和问题。

数列问题是一个高考热点，可以说，数列知识是一个必须掌握的必考知识。学生首先需要夯实基础，对等差（比）数列的求和、概念、性质、通项公式等做到烂熟于心，定期整理相关知识，掌握每种题型的解决方法，在练习中很快找准方法解题。这就需要学生将老师讲的每种题型内化，做到解题过程中运用自如。数列的综合题目也十分常见，需要学生构建自己的知识体系，明白数列与其他知识之间的关联，不断总结和修改自己的思维导图。另外，数列问题中往往涉及大量的运算，需要学生具有较高的计算能力，做到正确且迅速地计算出答案。