利用表格分析法巧解一元一次方程的实际运用

广东省中山市坦洲实验中学 张永忠

列方程解应用题是初中数学学习的重点和难点之一，难在综合性较强，涉及的知识面较广，要求学生具有一定的分析问题和解决问题的能力。而七年级学生分析问题、寻找数量关系的能力较差，所以在学习的过程中经常会出现一些意想不到的错误。笔者根据多年的教学经验，提出巧用表格分析法有效突破这些难点。

一、表格的设计

表格分析法的关键在于表格的设计，如何创建表格？我们要先考虑表格的横向与纵向。横向表示各数量，例如：已知量、未知量、第三个数量，纵向表示两者的比较。

二、表格填写的基本步骤

首先，弄清题意，可以引导学生仔细读题，审清题意，题目中包含几个对象？存在哪几个量？这些量之间存在什么关系？再弄清楚哪些是已知量？哪些是未知量？然后纳入表格。

其次，通过假设其中的一个未知量为x，根据题意条件中的语句“翻译”成含未知量x的式子，表示另一个对应的未知量，后根据已知量和未知量之间的关系表示出第三个数量式子，填入表格。

最后，寻求等量关系，一般根据题意分析出第三个数量之间的关系，布列方程。

三、表格分析法解一元一次方程问题的具体应用

1.“和、差、倍、分”问题

【例1】今年“六一”儿童节，张红用8.8元钱购买了甲、乙两种礼物，甲礼物每件1.2元，乙礼物每件0.8元，其中甲礼物比乙礼物少1件，问甲、乙两种礼物各买了多少件？

【解析】题中的等量关系有：

买甲礼物的费用＋买乙礼物的费用=8.8元 ①

乙礼物的件数－甲礼物的件数=1 ②

设购买甲礼物为x件，填写下表：

单价 数量 费用甲礼物 1.2 x 1.2x乙礼物 0.8 x+1 0.8（x+1）

根据“总价”，利用等量关系①列出方程：

1.2x+0.8（x+1）=8.8，

解得x=4，∴x+1=5。

答：甲礼物买了4件，乙礼物买了5件。

【同源练习】小辉同学用100元购买了10本笔记本和5本草稿本，其中笔记本每本7元，问草稿本多少元一本？

2.“行程、工程、顺逆”问题

【例2】某工程，甲一个人要20天完成，乙一个人10天就能完成。现要求甲、乙两人在12天内完成任务，问乙需工作几天后，甲再继续加工才可按期完成任务？

【解析】工作总量看作整体“1”，设乙需工作x天后，甲再继续加工才可正好按期完成任务，列表如下：

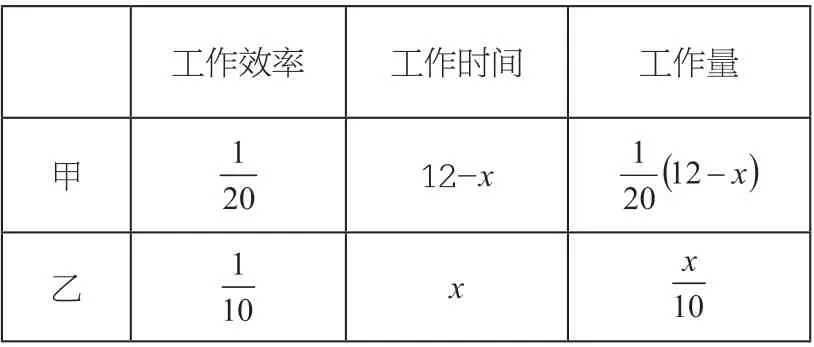
工作效率 工作时间 工作量甲12-x乙x

根据“工作量”，利用等量关系：

甲完成的工作量+乙完成的工作量=总工作量（“1”）

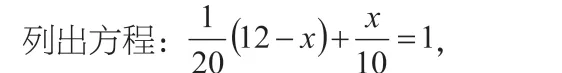
解得x=8。

答：乙需工作8天后，甲再继续加工才可正好按期完成任务。

【同源练习】已知甲、乙两地相距120千米，乙每小时走的路程比甲每小时走的路程多1千米。甲先从A地出发2小时后，乙从B地出发，与甲相向而行，经过10小时后相遇，求甲、乙的速度。

3.“利润、利息”问题

【例3】某商场将某貂皮衣服按原价的八折出售，此时貂皮衣服的利润率是10%，已知这种貂皮衣服的原价为2475元，那么这种貂皮衣服的进价是多少元？

【解析】设这种貂皮衣服的进价为x元，列表如下：

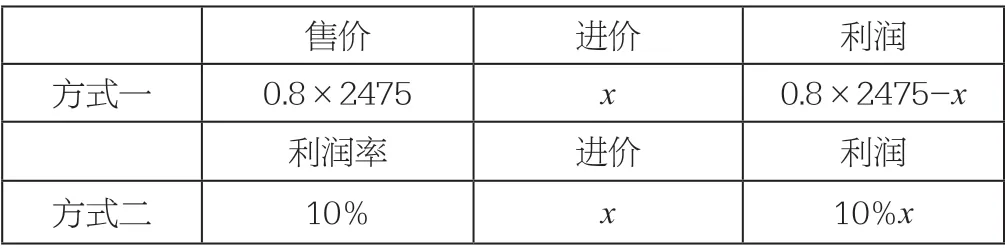
售价 进价 利润方式一 0.8×2475 x 0.8×2475-x利润率 进价 利润方式二 10% x 10%x

根据“利润”，找相应的等量关系：售价－进价=利润率×进价，

列出方程：0.8×2475-x=10%x，

解得x=1800。

答：这种貂皮衣服的进价为1800元。

【同源练习】某商场开展优惠活动，所有商品一律按八折优惠出售，已知某种鞋子进价30元一双，九折出售后，商家获利润率为20%，问这种鞋子标价是多少元？优惠价是多少元？

列方程解应用题的实质就是将实际问题转化为数学问题，再由数学问题的解决带来实际问题的解决，这个过程中最关键的步骤是“找出应用题中数量间的相等关系，列出方程”，为了突破这一教学难点，借助表格分析法思路清晰，方法较为简单实用，利于学生接受和理解，能够有效培养学生分析问题和解决问题的能力。