嵌入式系统软件工作量多源线性估算方法仿真
2021-11-17夏双成
夏双成
(长春工业大学人文信息学院,吉林 长春 130000)
1 引言
嵌入式系统软件工作量的估算是计划开发软件的基础,为软件项目制定合适的开发计划,是软件项目管理的核心。软件工作量估算是其中的主要部分,估算结果是否正确也十分重要,软件工作量较低的估算会影响软件项目的完成时间,较高的估算将会增加成本[1],导致公司承担较高的费用。估算软件工作量一直是一个难题,首先,软件的本质使软件具有不可见性和复杂性;其次,由于项目经验数据不断减少,或者新技术的应用和出现使经验数据无效,导致评估参考准确性差,同样也会影响软件工作量估算结果的可信度[2];最后,软件工作量评估人员的一些主观因素也会影响软件工作量的估算。目前,软件组织和部分学者也开始投入到嵌入式系统软件工作量估算的研究中。
亓卓亚[3]提出软件项目中软件工作量多源线性估算方法,首先,给出软件工作量估算方法,并对COCOMO模型估算方法进行了简单介绍;其次,对软件工作量估算中项目规模度量方法,主要对功能点分析方法进行了描述;最后,利用三步法对软件工作量进行多源线性估算,实验结果表明,该方法合理性较高。盛玉强和杨春花[4]提出基于软件量化的嵌入式系统软件工作量多源线性估算方法,对软件开发过程进行量化,可以获得量化数据,对量化数据进行统计和分析来确定其指标,在此基础上,对嵌入式系统软件工作量进行估算,实验结果表明,该方法简单合理。但是以上两种方法对软件工作量估算的平均误差率较高,不能够准确的完成对软件工作量的估算。张文等[5]人对嵌入式系统工作量多源线性估算方法展开了相应研究,对软件工作量数据缺失内在机理进行介绍,利用朴素贝叶斯算法对嵌入式软件工作量进行估算,实验结果表明,该方法可以对工作量的缺失数据进行处理,但该方法存在软件工作量估算效率低的问题。
针对上述三种研究结果中存在的问题,提出基于灰色关联分析的嵌入式系统软件工作量多源线性估算方法。建立软件度量数据模型,并计算软件项目之间的关联度,以嵌入式系统软件项目的历史数据为基准,采用灰色关联分析方法对嵌入式系统软件工作量进行估算。研究表明,本文方法软件工作量的估算平均误差率较低、估算效率较高,可以准确、有效的完成对软件工作量的估算。
2 基于灰色关联分析的工作量多源线性估算
2.1 软件度量数据模型
统计学中的回归分析方法可以解决软件工作量中相互关联变量之间的关系,多元线性回归模型是指变量Y和多个变量X1,X2,…,Xk间的线性关系,假设Y和X1,X2,…,Xk间存在线性关系,并且为变量的多元线性函数,称其为线性回归模型,有如下表达式
Y=β0+β1X1+β2X2+…+βkXk+μ
(1)
式中,Y表示因变量,Xj(j=1,2,…,k)表示k个自变量,βj(j=0,1,2,…,k)表示k+1个未知参数,μ表示随机误差[6],通常情况下,设μ~N(0,σ2)。
因变量Y和自变量X1,X2,…,Xk的线性方程如下
E(Y)=β0+β1X1+β2X2+…+βkXk
(2)
式(2)被称作总体回归方程。对于n组观测值X1i,X2i,…,Xki(i=1,2,…,n),方程组为
Yi=β0+β1X1i+β2X2i+…+βkXki+μi
(3)
式中,μi表示第i个随机误差。即
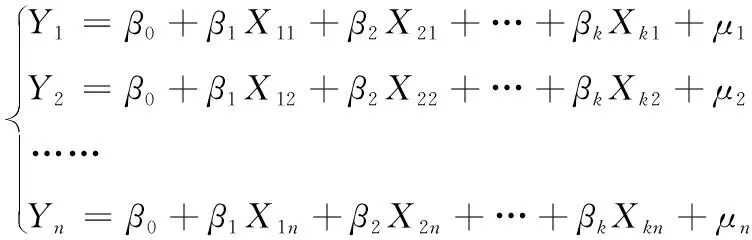
(4)
矩阵表达式如下

(5)
即
Y=Xβ+μ
(6)
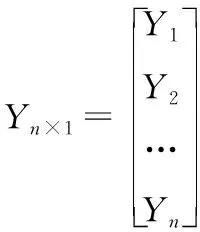
总体回归方程如下
E(Y)=Xβ
(7)
根据观测样本对模型中的参数进行估计,并统计和检验回归方程和估计参数,多元线性回归模型中有多个因变量[8],多个因变量同时对自变量产生作用,若观察一个因变量对自变量的影响,需要假定其它因变量不变来展开分析。
参数β0,β1,β2,…,βk为未知,采用样本观测值来估计以上参数,假设计算获得的估计值为0,1,2,…,k,利用参数的估计值来代替β0,β1,β2,…,βk,可以得到如下方程
i=0+1X1i+2X2i+…+kXkn
(8)
=X
(9)
样本回归方程所获得的因变量Yi和i间的偏差为残差ei,表达式为
ei=Yi-i=Yi-(0+1X1i+2X2i+…+kXkn)
(10)
根据获得的残差,构建软件度量数据模型U,其表达式为
U=eiβ
(11)
在选取样本的过程中,样本的容量需要满足
1)最小样本容量:以最大自然和最小二乘法原理为基础,可以获得参数的估计量,其容量必须大于软件度量数据模型中自变量的数量,由此得到样本容量大于n+1。
2)符合基本要求的容量。从参数的估计角度出发,容量应该是自变量数量的5倍多;从检验有效性的方面来说,应大于30。
3)在大样本下,软件度量数据模型的性质可以得到证明。
构建回归方程时,估计模型中的参数有利于检验软件度量数据模型的有效性。
2.2 软件工作量多源线性估算
嵌入式系统软件项目的历史数据,为软件工作量估算提供了理论依据,建立软件项目的历史数据对软件工作量估算的准确性起着重要作用,采用软件项目历史数据可以避免对软件工作量估算过程中出现的无依据性和主观性,对采集数据进行定义以及数据的采集是构建软件项目历史数据的两个任务。在构建软件度量数据模型的基础上,以嵌入式系统软件项目的历史数据为基准,对嵌入式系统软件工作量进行估算研究。
嵌入式系统软件工作量的估算属于比较复杂的系统工程。通常情况下,利用特征对软件项目进行描述,特征也能够对嵌入式系统软件工作量展开估算,软件项目特征给软件工作量所带来的影响不同,在估算前需要将影响最大的特征选取出来。过程为:将软件项目特征当作比较序列,将软件工作量当作参考序列,采用灰色关联分析方法对软件工作量和项目特征间的关联度进行计算;随后,按照回归技术选出最优项目特征集合,采用灰色关联分析方法对嵌入式系统软件工作量进行估算。

嵌入式系统软件项目集合D的矩阵表达式如下
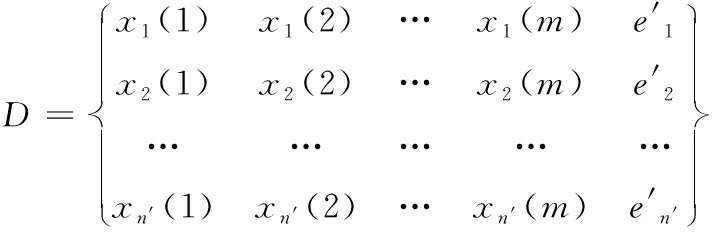
(12)
灰色关联分析方法确定软件项目子集的步骤为建立参考和比较数列。将D的每一列当作一组数据,可以获得数列
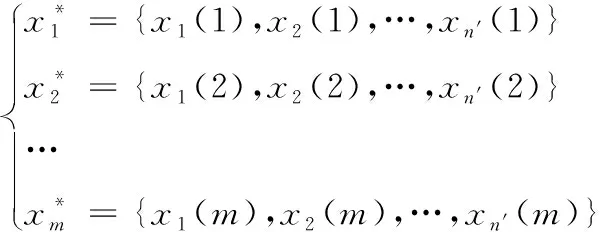
(13)

(14)

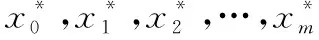
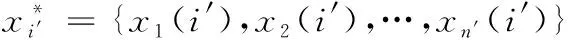
(15)
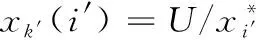
(16)
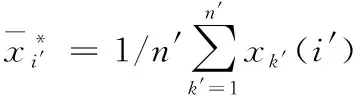
(17)

对灰色关联度进行计算。在计算比较和参考序列灰色关联度的过程中,关联度越大说明软件项目特征对工作量越重要。在计算关联度时,需要分析不同软件项目特征所带来的影响,可以提高计算的准确度。
当x0(k′)与xi′(k′)为数值型特征时,有
Δi′k′=|x0(k′)-xi′(k′)|
(18)
当x0(k′)与xi′(k′)为类别型特征时,有

(19)
按照灰色关联度构建软件工作量和软件项目特征的关联序χf。
采用回归技术选择最优软件项目特征集合Sbest,步骤为
1)将χf中对嵌入式系统软件工作量带来最大影响的特征放入Sbest中;
2)对平均误差进行计算;
3)将χf中的剩余项目特征添加在Sbest中;
4)按照最优项目特征集合Sbest对软件工作量进行估算,添加项目特征之后软件工作量估算的平均误差率较高时,则删除该特征集合;
5)判断χf中的项目特征是否添加结束,结束则终止算法,输出Sbest。
在确定了最优软件项目特征集合之后,采用灰色关联分析方法对软件工作量进行估算。步骤如下:
1)构建数据集。将D1的每行当作一组数据,参考序列为
x0={x1(1),x1(2),…,x1(q)}
(20)
比较序列为
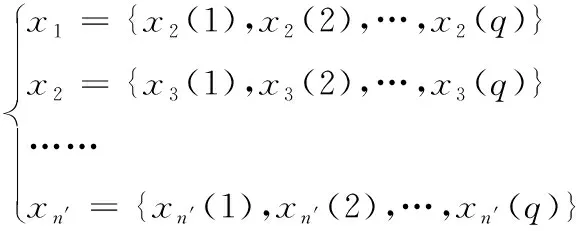
(21)
式中,q代表Sbest中软件项目的特征数量。
2)标准化处理。利用均值化变换方法做标准化处理,可以去除不同纲量对灰色关联分析方法带来的影响。
3)计算灰色关联度。
4)估算软件工作量。根据计算结果,确定x0与x1,x2,…,xn′的关联序ωi′,采用关联度较大的ι个软件项目对x0的软件工作量进行估算

(22)

(23)
3 实验设计与结果分析
基于灰色关联分析的嵌入式系统软件工作量多源线性估算方法的实验开发环境为:操作系统为WindowsXP,服务器为Tomcat5.5,数据库为Microsoft SQL2000,开发工具为Eclipse。为了验证本文方法的有效性,选取某公司网站的嵌入式系统,图1为嵌入式系统软件结构。

图1 嵌入式系统软件结构
根据嵌入式系统的需求分析和概念设计,采用本文方法、文献[3]方法和文献[4]方法对其进行工作量估算。估算结果如表1所示。
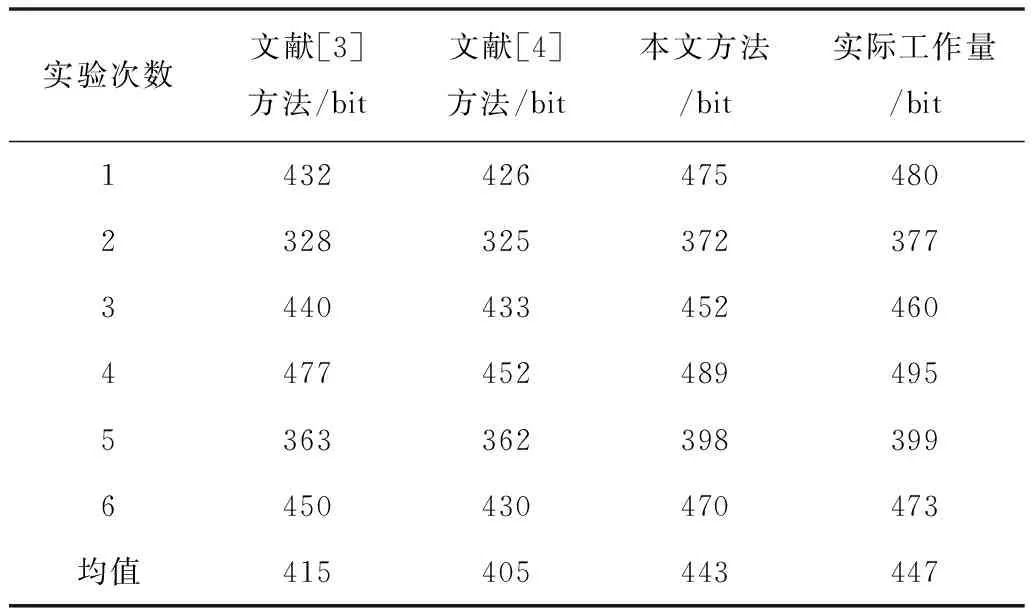
表1 工作量估算结果对比
根据表1可知,文献[3]方法的工作量估算平均结果为415;文献[4]方法的工作量估算平均结果为405;本文方法的工作量估算平均结果为443,仅与实际工作量估算平均结果差5 bit,本文方法的工作量估算结果更接近实际的工作量估算结果。说明本文方法的工作量估算准确性较高。
为了验证软件工作量估算方法的有效性,对其估算的误差率展开实验研究,误差率越高,估算的越不准确,测试结果如图2所示。

图2 不同方法的工作量估算误差率对比
分析图2可知,在对嵌入式系统软件工作量进行估算的过程中,对本文方法与文献[3]方法、文献[4]方法的估算误差率展开了相应的测试。对比可知,文献[3]方法在进行工作量估算时,呈现散点状态,估算误差率最高;而本文方法的工作量估算误差率最低,其次是文献[4]方法,说明本文方法所得到的估算结果更加准确。
在对嵌入式系统软件工作量估算平均误差率测试的基础上,进一步测试软件工作量的估算效率,测试结果如图3所示。

图3 不同方法软件工作量的估算效率对比结果
分析图3可知,本文方法软件工作量为200小时的估算效率为60%,文献[5]方法软件工作量为1400小时的估算效率为60%,本文方法工作量1400小时的估算效率为90%,对比可知,本文方法最少工作量的估算效率与文献[5]方法最多工作量的估算效率相同,说明本文方法软件工作量的估算效率更高。
4 结论
为了深入研究有关嵌入式系统的软件工作量,提出基于灰色关联分析的嵌入式系统软件工作量多源线性估算方法,分别对软件工作量估算的误差率和效率展开了相应测试。
1)提出方法软件工作量估算的误差率较低,并且还具有较高的估算效率,可以准确且有效的实现对嵌入式系统软件工作量的估算,同时也验证了提出方法的有效性。
2)提出方法在传统方法的基础上将软件工作量当作参考序列,采用灰色关联分析方法对软件工作量和项目特征间的关联度进行计算,从而提高计算的准确度;并采用灰色关联分析方法对嵌入式系统软件工作量进行估算,提高了软件工作量的估算效率。
3)提出方法还能够为软件工作量估算的下一步研究提供参考意见,为软件项目的开发奠定了实用性的基础。
