一种基于局域不可区分正交直积态的新型量子保密求和协议

王 跃, 张可佳,2, 蔺苗苗

(1.黑龙江大学 数学科学学院, 哈尔滨 150080; 2.黑龙江大学 黑龙江省复杂系统与计算重点实验室, 哈尔滨 150080)

0 引 言

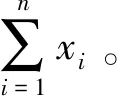
通过上述的分析，发现量子保密求和协议能通过不同的量子载体来实现，例如单光子[19]、Bell态[20]和d维纠缠态[21-22]等。最近，一种具有局域不可区分性的正交直积态引起了研究者们的广泛关注。区别于单光子和纠缠态，这种新型量子态在局域操作和经典通信下不可区分，并且相比于纠缠态更容易制备。将这种量子态应用于量子密码协议的设计中已成为研究者们关注的热点，例如，基于正交直积态的量子密钥分配协议[23]、基于正交直积态的量子秘密共享协议[24]、基于正交直积态的量子代理签名协议[25]、基于正交直积态的量子支付协议[26]、基于正交直积态的多方量子签名协议[27]和基于正交直积态的量子投票协议[28]等。进一步，本文考虑将这种具有局域不可区分性的正交直积态用于量子保密求和协议设计中。

本文介绍了在协议中所用到的一些基础知识，包括量子保密求和协议所应该满足的一些基本条件和协议的基本流程，分析了协议的正确性、隐私性和安全性，并对后续的研究内容进行了讨论和总结。

1 预备知识

首先介绍协议中所使用的正交直积态。在3⊗3量子系统中，可以构造以下9个正交直积态：

|φ1〉=|1〉1|1〉2

|φ2,3〉=|0〉1|0±1〉2

|φ4,5〉=|0±1〉1|2〉2

(1)

|φ6,7〉=|2〉1|1±2〉2

|φ8,9〉=|1±2〉1|0〉2

随后，移位操作Ux定义如下：

(2)

式中：d为量子系统的维数，⊕为模d加，x=0,1,2，…,d-1。不难发现，对处于计算基下的量子态|t〉，t=0,1,2，…,d-1，执行Ux操作之后可得：

Ux|t〉=|t⊕x〉

(3)

(4)

2 基于局域不可区分正交直积态的量子保密求和协议

2.1 协议满足的条件

在协议中，假设有3个参与者P1、P2和P3，每个参与者Pi手中有一个长为N的秘密串：

(5)

X=(x1,x2,…,xN)

(6)

基于上述条件，量子保密求和协议应该满足以下三个条件：

(1) 正确性： 每个参与者Pi输入了自己的秘密数值Xi后，所有参与者经过一系列计算最终能够得到正确的X。

(2) 隐私性： 每个参与者Pi除了得到求和的结果X之外，不能获得其他参与者Xj(j≠i)的值。

(3) 安全性： 当外部的窃听者想要获得参与者Pi的秘密信息Xi时，就一定会被参与者P1检测到。

2.2 协议的具体步骤

在3⊗3量子系统中，量子保密求和协议的具体步骤如下：

(1) 必要信息分发：首先，P1与P2和P3通过量子密钥分配(QKD)技术共享相同的密钥K=(k1,k2,…,kN)， 其中kj=0,1，j=1,2,…,N。这里要求密钥串K是均匀的，即其中0,1比特数相同。注意，当N的值为奇数时，在末位加kN+1=0。其次，P1制备N个量子态，每个量子态的形式随机取自公式(1)的正交直积态，并且这N个量子态中包含公式(1)中的9个量子态。然后，P1将这N个量子态中的第一个粒子取出，形成序列S1=(|s11〉,|s12〉,…,|s1N〉)；第二个粒子取出，形成序列S2=(|s21〉,|s22〉,…,|s2N〉)。同时，P1制备δ个随机选自{|0〉,|1〉,|+〉,|-〉}的诱骗粒子，将这δ个粒子插入S1中得到S′1，再制备δ个诱骗粒子插入序列S2中形成S′2。最后，将序列S′1发送给P2，将序列S′2发送给P3。

(2) 秘密信息编码：P2接收到S′1之后，P1公布诱骗粒子的位置和测量基。P2通过P1公布的测量基测量对应位置的粒子，然后P1和P2比对测量结果与P1初始制备的诱骗态是否相同。若错误率高于某个阈值，协议终止；否则，协议继续，P2恢复序列S1。P2根据手中的密钥K对粒子执行相应的操作生成新的序列T1：

(7)

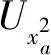
(8)

最后，P3在新的序列R1中随机插入δ个诱骗粒子得到R′1并发回给P1。

类似地，P3在接收到S′2之后，对诱骗粒子进行检测。检测通过后，P3去除δ个诱骗粒子，序列由S′2变为S2，同样根据密钥K对粒子序列执行操作得到新的序列T2：

(9)

(10)

最后，P2在新的序列R2中随机插入δ个诱骗粒子得到R′2并发回给P1。

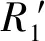
(11)

(4) 计算求和结果：P1首先使用相应的基测量余下的N个量子态，可以通过表1来获得求和的结果：

(12)

然后，P1公布计算结果。具体参与方之间交互的过程如图1所示。

图1 协议流程图

3 协议分析与讨论

3.1 正确性

(13)

(14)

(15)

(16)

P3将粒子发送给P1。第三步检测窃听阶段，P1收到粒子R1和R2后，将自己的秘密编码到粒子上：

(17)

第四步计算求和结果，P1使用相应的基对两个粒子分别进行测量，将测量结果对应表1得到求和结果E=(0,2)并公布。由此可知，协议可以得到正确的求和结果。

表1 执行移位操作之后相对应的结果

3.2 隐私性

隐私性即协议可以抵抗内部参与者Pi所发起的攻击。由于Pi参与了协议执行的过程，所以他发起的攻击往往比外部窃听者Eve的攻击更具危险。内部参与者攻击可以分为两种，第一种是单个不诚实参与者攻击，第二种是两个及两个以上多个不诚实参与者的联合攻击。由于在实际中假设大多数参与者都是诚实的，因此在三个参与者的情况下，我们只需要考虑参与者的单独攻击即可。单个不诚实参与者的独立攻击又分为以下两种情况：

(1) 参与者P2或P3发起的攻击

由于参与者P2和P3攻击手段相同，所以这里只分析P2所发起的如下攻击：①P2窃取P1的秘密信息。由于P1的秘密信息是在粒子传输完回到自己手中后才编码到粒子上的，所以P2无法获得P1的秘密信息。②P2窃取P3的秘密信息。P2在第二步秘密信息编码过程中，可能会实施截获-测量-重发攻击和纠缠-测量攻击。

(18)

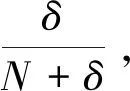
(19)

故而，P2得到正确的测量结果并且不被发现的概率为：

(20)

当N足够大时，可能性趋近于零。P2测量完粒子后，根据测量结果，伪造粒子发送给P1。P1接收粒子后与P3一起检测窃听，当错误率高于某个阈值时，终止协议。

然后，以粒子{|0〉,|1〉,|0+1〉,|0-1〉}为例，来分析纠缠-测量攻击。P2拦截了由P3发送给P1的粒子序列之后，制备辅助粒子|A〉，并对拦截的粒子和辅助粒子执行如下操作：

U|0〉|A〉=α|0〉|a00〉+β|1〉|a01〉

U|1〉|A〉=γ|0〉|a10〉+δ|1〉|a11〉

(21)

式中|α|2+|β|2=|γ|2+|δ|2=1，为了不改变截获粒子的状态，式(21)需要满足：

β|a01〉=γ|a10〉=0

α|a00〉-β|a01〉+γ|a10〉-δ|a11〉=α|a00〉+β|a01〉-γ|a10〉-δ|a11〉=0

(22)

由式(21)和式(22)得：

U|0〉|A〉=α|0〉|a00〉

U|1〉|A〉=α|1〉|a00〉

(23)

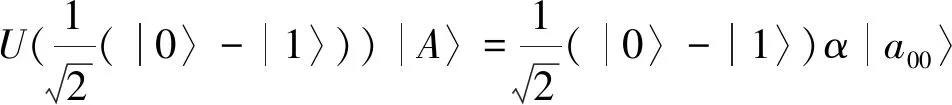
由此可见，P2不能通过对辅助粒子的测量获得P1的秘密信息。综上所述，参与者P2或P3发起的攻击是无效的。

(2)量子态的制备者P1发起的攻击

P1要想窃取P2和P3的输入数值，会在第二步秘密信息编码阶段拦截由P2发送给P3的N+δ个量子态。P1是量子态的制备者，可以选择相应的测量基对N个编码秘密信息的粒子进行测量。由于不知道δ个诱骗粒子所处的位置和测量基，所以发送伪造粒子给P3之后，P3与P2将会以如下p的概率发现P1的窃听行为：

(24)

当N足够大时，p趋近于1。因此，本协议可以抵抗参与者P1发起的攻击。

3.3 安全性

安全性即协议可以抵抗外部窃听者Eve的攻击。假设存在一个外部攻击者Eve，在量子态的传输过程中想要实施一些窃听行为。在第二步秘密信息编码过程中，P1制备量子态之后，量子态以环形传递。Eve获取由Pi发送给Pi+1的量子态，其中i=1,2，它对粒子可能实施截获-测量-重发攻击和纠缠-测量攻击。然而，由于Eve不知道密钥K的值，攻击将改变处于kj=0位置的粒子，其中j=1,2,…,N，从而在检测窃听阶段被P1发现，进而中止协议。

3.4 讨论

仅利用3⊗3量子系统中的局域不可区分正交直积态来设计量子保密求和协议，这种思想也可以在d⊗d量子系统中实现。如在4⊗4量子系统中，可以通过与3⊗3量子系统同样的方式构建一个量子保密求和协议。协议的具体步骤除第一步必要信息分发中P1所制备的N个量子态不同之外，其他步骤与上述的协议步骤相同。

表2 执行移位操作之后相对应的结果

P1在如下的4⊗4量子系统中的局域不可区分正交直积态中选择N个量子态：

|φ1〉=|0〉|0〉 |φ10,11〉=|0±3〉|1〉

|φ2,3〉=|1〉|0±1〉 |φ12,13〉=|3〉|0±3〉

|φ4,5〉=|0±1〉|2〉 |φ14〉=|1〉|3〉

|φ6,7〉=|2〉|0±2〉 |φ15〉=|2〉|1〉

|φ8,9〉=|0±2〉|3〉 |φ16〉=|3〉|2〉

4 结 论

本文给出了将局域不可区分正交直积态应用于量子保密求和协议中的新方法，这之中还存在着一些没有考虑到的一些情况，例如如何利用局域不可区分正交直积态在n个参与方中进行保密求和等等。相信随着关于正交直积态研究的深入，这些问题都能够得到有效的解决。本文基于局域不可区分正交直积态设计了一种新型的三方量子保密求和协议。理论分析表明，本协议可以确保正确性、隐私性和安全性。