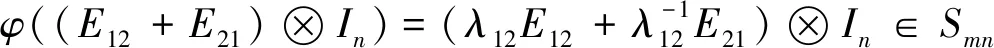保对称矩阵张量积秩的线性映射

邓 琳, 徐金利

(东北林业大学 理学院, 哈尔滨 150040)

0 引 言

设Mm和Sm分别是复数域上m×m全矩阵和对称矩阵全体。Eij表示矩阵单位,In和0分别表示单位矩阵和零矩阵, ⊗表示矩阵的张量积。 1959年, Marcus等最早刻画了保矩阵秩的线性映射[1], 之后Beasley等给出了Sn上保持秩k线性映射的形式[2], Zhang刻画了不同对称矩阵空间之间保持秩的线性映射[3]。

引理1[3]设L是Sm到Sn的线性映射, 则

rankL(A)=rank(A), ∀A∈Sm

(1)

当且仅当m≤n并且存在可逆阵P∈Mn,使得

2012年, 著名矩阵论专家李志光教授在矩阵与算子国际会议上提出刻画保持矩阵张量积秩的线性映射问题[4], Zheng等随后给出该问题的回答[5]。近年来, 很多学者对矩阵张量积上各种保持问题进行了大量的研究, 参看文献[6-14]。

本文考虑保持对称矩阵张量积秩的线性映射:

定理1线性映射φ:Sm⊗Sn→Smn保持矩阵张量积秩, 即：

rankφ(A⊗B)=rank(A⊗B), ∀A∈Sm,B∈Sn

(2)

当且仅当存在可逆阵P∈Mmn，使得

φ(X)=PXPt, ∀X∈Sm⊗Sn

1 相关引理

引理2设U,V∈Mn是可逆阵。如果

XU=VX, ∀X∈Sn

(3)

则U=V=λIn, 其中λ∈*。

Matsaglia等在1974年得到如下的引理:

引理3[15]设m,n,r是正整数, 满足mr≤n。如果Xk∈Sn,k=1,…,m满足

则存在可逆阵U,V∈Mn满足

Xk=U((Ekk⊗Ir)⊕0n-mr)V,k=1,…,m

引理4设k,m,n是正整数满足k≤m,A,B∈Sn是可逆矩阵。如果X∈Smn满足

(4)

则存在Y∈Mn，使得

X=Eij⊗Y+Eji⊗Yt

证明不失一般性, 不妨设i=1,j=2。

由于A,B是可逆的对称矩阵, 所以存在可逆阵U,V∈Mn使得A=UUt，B=VVt, 再记

式中：X11,X22∈Sn，X33∈Smn-2n。

由式(4)得到

记tanθ=λ, 则有

由于使得det(λ-1In+X11)≠0的λ有无穷多个, 对这些λ有

进而

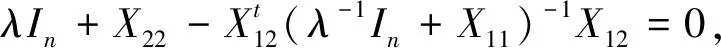
式中adj(λ-1In+X11)是(λ-1In+X11)的伴随矩阵。注意到det(λ-1In+X11)是关于λ-1的n次多项式, 而adj(λ-1In+X11)的每个位置元素均是关于λ-1的至多n-1次多项式。 因此有

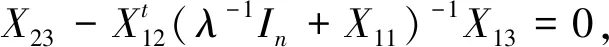
2 保对称矩阵张量积秩的线性映射刻画

定理5充分性是显然的， 由于必要性的证明较长, 分成以下两个命题:

命题6设Ak∈Sm,k=1,…,m满足

则存在可逆阵U∈Mmn使得对任意的k=1,…,m，有

φ(Ak⊗B)=U(Ekk⊗B)Ut, ∀B∈Sn

证明因为

rank(Ak⊗In)=n,k=1,…,m

和

所以

rank(φ(Ak⊗In))=n,k=1,…,m

及

由引理3知, 存在可逆矩阵U,V∈Mmn，使得

φ(Ak⊗In)=U(Ekk⊗In)V,k=1,…,m

记VU-t=[Fij],Fij∈Mn，并注意到φ(Ak⊗In)∈Smn，有

φ(Ak⊗In)=U(Ekk⊗In)(VU-t)Ut

因为

所以当j≠k时Fjk=0, 于是U(Ekk⊗In)(VU-t)Ut=U(Ekk⊗Fkk)Ut。 由于

rankFkk=rankφ(Ak⊗In)=n

将φ与映射X复合, 复合后的映射仍然满足式(2), 因此不妨设

φ(Ak⊗In)=Ekk⊗In,k=1,…,m

(5)

对k=1,…,m，定义Lk:Mn→Mmn,

Xφ(Ak⊗X)

由于rankAk=1，所以对任意的B∈Sn,有

rank(B)=rankLk(B)

这说明Lk是从Mn到Mmn的保对称矩阵秩的线性映射, 对Lk应用引理1知, 存在可逆矩阵Rk∈Mmn使得对任意的X∈Sn，有

(6)

由式(5)和式(6)可得

(7)

令

即

将上式代入式(6)得到

令

则对任意的X∈Sn,有

φ(Ak⊗X)=U(Ekk⊗X)Ut

这就证明了命题6。

对Ak=Ekk,k=1,…,m，应用命题1, 不妨设

φ(Ekk⊗B)=Ekk⊗B,k=1,…,m, ∀B∈Sn

(8)

命题7对任意的1≤i

φ((Eij+Eji)⊗B)=((λijEij+λjiEji)⊗B), ∀B∈Sn

(9)

证明为了方便, 仅对i=1,j=2时给出证明, 其他情况的证明是类似的。

令

由命题6, 存在可逆阵Q∈Mmn使得对任意的X∈Sn，有

φ(Ak⊗X)=Q(Ekk⊗X)Qt,k=1,…,m

(10)

由式(8)和式(10)可得

Ekk⊗X=Q(Ekk⊗X)Qt,k=3,…,m

(11)

记Q=[Qij]m×m, 式中Qij∈Mn。 取X=In, 由式(11)得

(Ekk⊗In)Q-t=Q(Ekk⊗In),k=3,…,m

因此

(12)

记

式中T11,T12,T21,T22∈Mn, 由式(8)、式(10)和式(12)可知，对任意的X∈Sn，有

(13)

及

(14)

另一方面, 注意到, 对任意可逆的B∈Sn和任意的λ∈C, 有

rank(cos2θ(E11⊗B)+sin2θ(E22⊗B)+sinθcosθ((E12+E21)⊗B))=n

由式(8)得

rank(cos2θ(E11⊗B)+sin2θ(E22⊗B)+sinθcosθφ((E12+E21)⊗B))=n

应用引理4得

式中YB∈Mn， 再由B∈Sn的任意性, 可知

(15)

式中Y(X)∈Mn。

取X=In, 由式(13)、式(14)和式(15)可得

2Q11T11=2Q22T22=2Q21T21=2Q12T12=In

这表明T11,T21和Q22是可逆阵， 再由式(13)、式 (14)和式(15)可得

由引理2得，(T11)-1T21=λ12In。 由式(13)和式(15)可得

如果m≥3, 则对1≤i

rank((Eii+Ejj+Ekk+(Eij+Eji)+(Eik+Eki)+(Ejk+Ekj))⊗In)=n

及φ的性质、式(2)和式(8)，结合命题2所得的结果可知

于是有

(16)

由式(16)得

λijλjk=λik

(17)

令

因为对任意的i=1,…,m,

及任意的1≤i

再由φ是线性映射, 结合式(8)和式(9), 对任意的A∈Sm,B∈Sn有

φ(A⊗B)=∑aiiφ(Eii⊗B)+∑aijφ((Eij+Eji)⊗B)

=∑aiiEii⊗B+∑aij(λijEij+λjiEji)⊗B

=∑aiiPEiiP⊗B+∑aij(P(Eij+Eji)P)⊗B

=(P(∑aiiEii+∑aij(Eij+Eji))P)⊗B

=(PAP)⊗B=(P⊗I)(A⊗B)(P⊗I)

这证明了定理5的必要性。