表面粗糙度对悬臂梁小试样蠕变性能评价的影响研究

曹舒凯，史 浩，谈建平，王卫泽，周帼彦，涂善东

(华东理工大学，上海 200237)

0 引言

在石化、发电和航空等工业领域中，由于节能减排的要求，工艺过程都向着高温、高参数方向发展，许多设备和部件都需要在高温、高压环境下工作。由于材料长期在高温环境下服役，组织会发生劣化而产生蠕变，严重影响高温结构完整性，因此,蠕变断裂是高温结构的主要失效形式之一[1]。获取材料高温蠕变性能的常用方法是传统单轴蠕变试验，而单轴蠕变试样因其体积较大，易对设备造成较大损伤，应用受到限制，尤其对于一些在高技术领域中应用的薄板等微小结构、价格较为昂贵的设备(如炉辊等)，无法提供足够的材料来取样进行试验[2-5]。为满足高参数装备高效率、长寿命运行的发展需求，小试样蠕变技术应运而生[6-8]。

表面取样技术的发展，促进了小试样试验方法在服役构件材料性能测试中的应用[9]。小试样蠕变试验所需材料的体积小，可直接从服役构件中取样，对构件的结构破坏较小[10]。但由于所用试样的尺寸较小，试验中的微小误差便会对测量结果造成较大影响。小试样试验中的影响因素有试样厚度、压头尺寸和接触状态等，不同因素对不同试验方法的影响程度亦不同[11]。在小试样蠕变试验过程中，载荷通过压头施加到试样表面，压头与试样表面之间存在接触，且接触状态在试验过程中不断变化，试样与压头之间的摩擦势必会影响试样的变形，从而影响对试样蠕变性能的评价。在高温环境下，加载压头与试样接触的摩擦尤为显著[12]。悬臂梁小试样蠕变变形过程中，压头与试样的接触位置逐渐改变，摩擦力会使试样中产生相应的切应力，进而对试样的蠕变变形产生影响。压头与试样接触点的摩擦力大小和压头尺寸有关，较大载荷下摩擦力的影响比较小载荷下的影响更显著[13]。文献[14-16]研究了试样与压头之间的摩擦对小冲杆试样断裂时间的影响，结果表明小冲杆试样的断裂时间受压头与试样之间的摩擦影响较大。同时，已有研究[17]指出小冲杆试样表征材料的性能必须考虑试样的表面接触条件。与小冲杆试样相比，悬臂梁小试样因载荷点位置偏置的特点而容易发生压头与试样的滑移，进而更容易受到接触摩擦的影响，而悬臂梁小试样的表面粗糙度对于试样蠕变性能评价的影响尚未有试验研究。

本文选取悬臂梁小试样为研究对象，基于Inconel 625 材料标准试样的蠕变试验得到的蠕变性能参数，采用诺顿蠕变模型建立悬臂梁小试样有限元模型，通过接触摩擦系数表征试样表面粗糙度，模拟试样蠕变变形曲线，并与试验相结合，研究表面粗糙度对悬臂梁小试样蠕变性能评价的影响。

1 试验方法

1.1 试样及装置

本研究中的材料为Inconel 625镍基合金，该材料在650 ℃下的高温力学性能如表1[18]所示。

表1 650 ℃下Inconel 625镍基合金高温拉伸试验结果

通过线切割和打磨的方法，加工3种表面不同粗糙度的悬臂梁小试样，试样试验段的尺寸为：19 mm(长)×1.9 mm(宽)×1.9 mm(高)，载荷跨距16 mm，试样的尺寸及试验装置简图如图1所示。

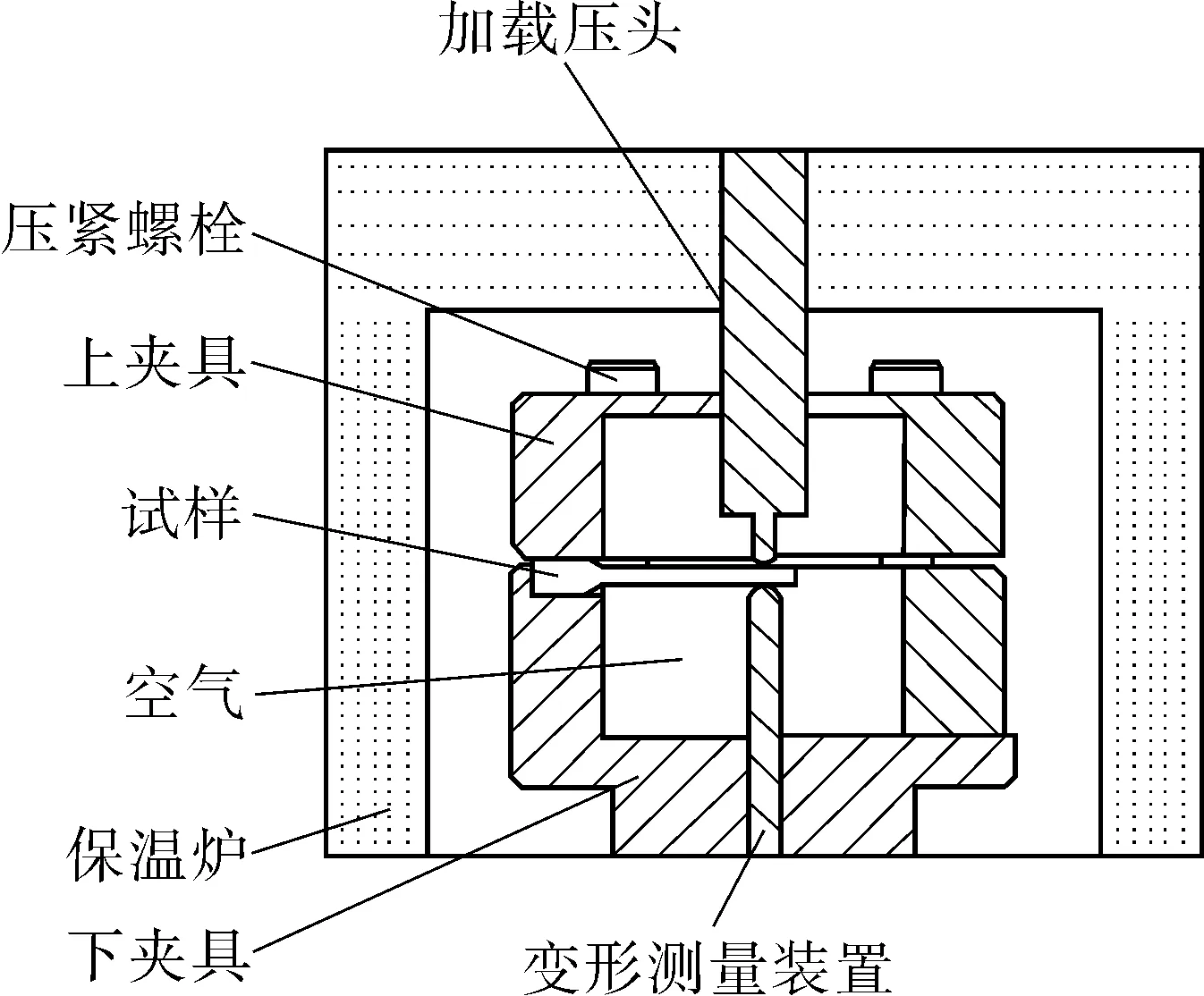
(a)试验装置

将试样夹持在上下夹具之间的开槽内，通过压紧螺栓固定试样，压头头部半径为1 mm。加载载荷恒定，通过直径3 mm的人造刚玉棒作为位移测量导杆，用NS-WY01型绕线式位移传感器测量试样载荷点位移，所有悬臂梁蠕变试验测试均在650 ℃的大气环境下进行。采用三维形貌仪对试样表面粗糙度进行标定，其表面粗糙度Ra分别为0.3,0.9,1.6 μm。

1.2 悬臂梁小试样与标准蠕变试样的关联

基于梁弯曲模型建立的悬臂梁小试样与标准蠕变试样之间等效应力的关系如式(1)[19]所示，悬臂梁小试样载荷点稳态位移速率与载荷之间的关系表达式如式(2)[20]所示。

(1)

(2)

蠕变试验载荷应小于对应温度下材料的屈服强度，基于式(1)及表1，载荷选取为28，32，36，40 N。

2 有限元模拟计算

2.1 蠕变本构方程

模型计算采用的蠕变本构模型是基于有效应力和应变等价性原理得到的单轴Kachanov-Rabotnov(K-R)损伤本构方程，广泛应用于蠕变损伤分析中，具体公式[21]如下：

(3)

(4)

2.2 有限元模型建立

悬臂梁小试样的有限元计算模型如图2所示。模型的几何尺寸为：l1=5 mm,l2=16 mm,l3=2 mm，h1=4 mm，h2=b=1.9 mm，L=24 mm，r=1 mm。本研究所用的材料Inconel 625镍基合金，在650 ℃下的K-R蠕变模型参数如表2[18]所示；分析中假设压头模型为刚体[22]，试样和压头之间为表面接触；对试验进行网格无关性验证，如图3所示，可以看出，当网格数量达到1 872个单元时，计算结果将不受网格数量影响，综合精度与成本，模型划分为2 484个单元，3 430个节点，单元类型为C3D8I；小试样蠕变有限元计算模型的载荷选取范围介于20～40 N。摩擦行为本质是由两个接触面上微观凹凸形貌之间的粘结、咬合作用等造成的，表面粗糙度的大小在宏观上反映的就是库伦摩擦系数的大小，因此在有限元模型中，定义3个接触摩擦系数来表征不同的表面粗糙度，即0.03，0.3，1.5，它们分别对应润滑状态、干摩擦状态、高摩擦状态等三种表面状态[23]。

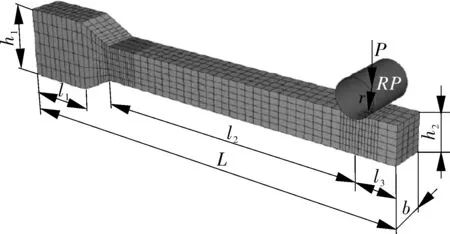
图2 悬臂梁弯曲小试样蠕变有限元模型 Fig.2 Creep finite element model of small bending specimens of cantilever beams

表2 650 ℃下Inconel 625镍基合金的K-R蠕变模型参数

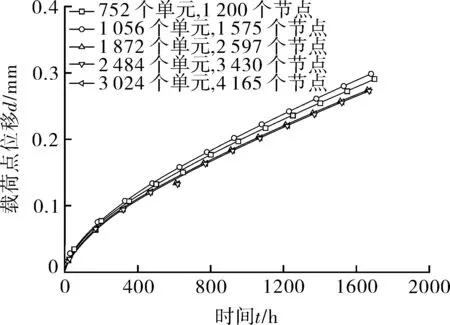
图3 网格无关性验证 Fig.3 Grid independence verification

3 结果与讨论

3.1 表面粗糙度对蠕变曲线的影响

悬臂梁小试样蠕变试验曲线及模拟曲线分别如图4,5所示。如图4所示，与文献[11]对小试样蠕变试验的研究结果相同，悬臂梁小试样蠕变试验难以得到蠕变第3阶段，仅能测得蠕变曲线的前两个阶段，即减速阶段和恒速蠕变阶段。基于试验数据，可以反推材料蠕变变形性能。整体上悬臂梁蠕变位移曲线随表面粗糙度的变化较大。随着表面粗糙度的增加，相同时间内试验的变形逐渐减小；摩擦系数对曲线的影响趋势与表面粗糙度基本一致，随着摩擦系数的增加，相同时间内蠕变变形减小。由此可见，用接触摩擦系数表征表面粗糙度的有限元计算具有一定的可行性，悬臂梁小试样有限元模拟基本符合试验结果，以下针对试验结果进行分析。

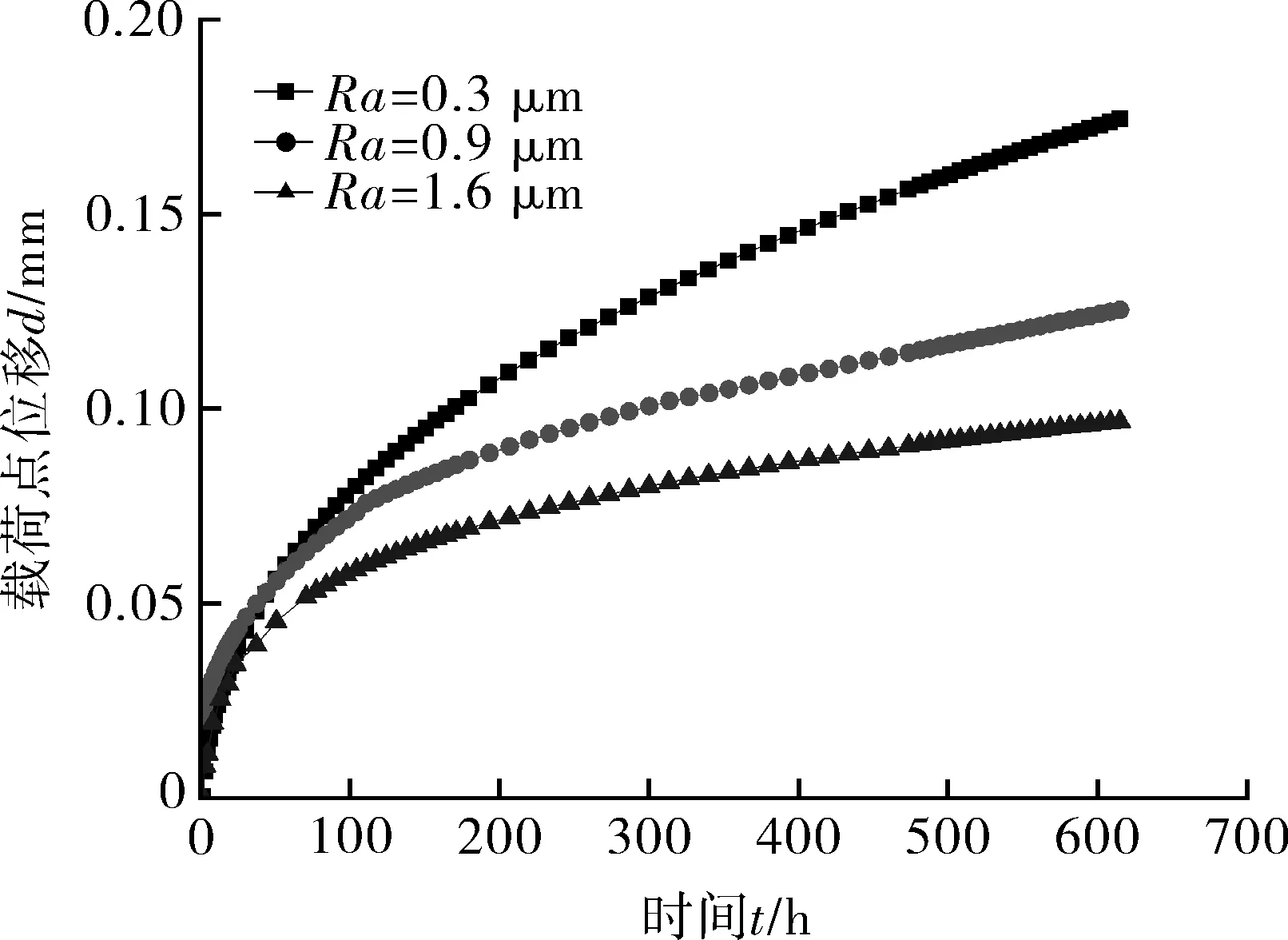
(a)P=28 N (b)P=32 N

(a)P=28 N

当试验载荷较小时，不同粗糙度试样在相同试验时间下的蠕变变形量较小。在28 N载荷下，蠕变变形量相差0.08 mm；而当载荷较大时，蠕变变形量相差较大，在40 N载荷下，蠕变变形量之差达到0.3～0.4 mm，差别可达30%。

悬臂梁弯曲小试样蠕变试验中仅存在压头与试样表面的接触，排除加工导致试样表面质量过差的因素，因此试样表面粗糙度对试样蠕变变形过程产生影响的原因，主要在于试样变形过程中，压头与试样表面的接触摩擦作用。当试样在载荷作用下发生变形，在载荷较小时，试样的蠕变变形量较小，压头与试样表面之间不会发生滑动。根据库伦摩擦理论，固体接触面是否发生相对滑动与最大静摩擦力有关，而接触的最大静摩擦力取决于接触摩擦作用；当载荷增大时，试验的变形量增大，压头与试样之间可能会产生相对滑动，而表面粗糙度较小的试样率先发生压头滑动，宏观上导致试样蠕变速率比表面粗糙度较大试样的速率大。

对温度650 ℃和载荷32 N的试验蠕变位移df和蠕变时间tf进行归一化处理，归一化位移d/df-归一化时间t/tf曲线如图6所示。可以看出，悬臂梁的归一化位移数据较为集中，受摩擦状态的影响较小；在蠕变第1阶段向第2阶段的过渡阶段内，位移数据出现明显分层，因此表面粗糙度对悬臂梁曲线的影响主要集中在蠕变第1阶段向第2阶段的过渡阶段。

图6 32 N载荷下悬臂梁弯曲小试样归一化位移d/df-归一化时间t/tf曲线 Fig.6 Normalized displacement-time (d/df-t/tf) curve of small bending specimens of cantilever beams under 32 N

3.2 表面粗糙度对稳态蠕变速率的影响

载荷点位移-时间曲线上一点的斜率即为试样在对应t时刻的蠕变速率，将图4中试样处于稳态蠕变阶段的原始数据进行线性拟合，可得到试样的稳态蠕变速率，不同载荷下试样表面粗糙度与试验稳态速率的关系如图7所示。可以看出，随着载荷增大，试样的稳态蠕变速率也增加，在同一载荷下，随着表面粗糙度的增大，试样的稳态蠕变速率减小，蠕变行为变缓。此外，表面粗糙度对试样的稳态蠕变速率的影响与载荷有关，当载荷较小时(如小于30 N)，随着表面粗糙度的增大，试样的稳态蠕变速率减小不明显；当载荷增大时(如32 N)，表面粗糙度对试样稳态蠕变速率有较明显的影响，表面粗糙度增大，稳态速率减小趋势相对显著。

图7 不同载荷下试样表面粗糙度Ra与稳态蠕变速率的关系曲线 Fig.7 Effect of surface roughness Ra on steady-state creep rate under different loads

3.3 表面粗糙度对蠕变参数反演的影响

基于梁弯曲理论及K-R蠕变损伤方程，悬臂梁小试样载荷点稳态位移速率与载荷之间的关系表达式如式(2)所示，对式(2)两边取以10为底的对数，可以得到：

(5)

其中：

(6)

由式(5)可知，悬臂梁小试样载荷点稳态位移速率与载荷在双对数坐标系下拟合成线性关系，进而求取蠕变参数，拟合曲线如图8所示，反演结果如表3所示。在反演过程中，蠕变应力指数n的精度会直接影响到B的精度，因此对蠕变应力指数n进行分析。不同表面粗糙度试样反演得到的蠕变参数n与表2中的理论值n=11.56的偏差在15%以内，这在材料的蠕变行为描述中是可以接受的。不同表面粗糙度试样反演得到的蠕变应力指数n值和蠕变常数B值存在一定差异。分析主要原因，认为所用解析模型是基于纯弯曲理论建立的，忽略剪应力的影响，只能近似地描述三点弯小试样的稳态蠕变变形规律，此外，拟合获取稳态蠕变速率的过程中也引入了误差。总体来说，不同粗糙度悬臂梁小试样载荷点稳态位移速率与载荷在双对数坐标系下拟合曲线相接近，蠕变参数反演结果存在一定差异，随着粗糙度的增加，反演得到K-R方程的参数B逐渐降低，因此认为在本研究范围内，不同表面粗糙度试样反演得到的蠕变应力指数n值和蠕变常数B值存在一定差异。

图8 载荷点稳态蠕变速率与载荷P的关系曲线 Fig.8 Relationship between steady-state creep rate of load point and load P

表3 试验蠕变参数反演结果

4 结论

本文以悬臂梁小试样为研究对象，采用摩擦系数表征表面粗糙度，用有限元模拟与试验相结合的方法分析了不同表面粗糙度下悬臂梁小试样蠕变性能评价的影响规律，得出如下结论。

(1)表面粗糙度对悬臂梁小试样蠕变变形有较大的影响，且试样表面粗糙度的影响与载荷有关。在相同载荷下，试验表面粗糙度增加，相同时间内蠕变变形量减小，稳态蠕变速率减小。当载荷较小(28 N)时，不同试样表面粗糙度对蠕变变形量和稳态蠕变速率影响较小；而当载荷较大(40 N)时，试样表面粗糙度对蠕变变形量的影响可达0.3～0.4 mm，稳态速率的减小趋势也更为显著。因此，在较大载荷时，试样的表面加工情况必须加以考虑。

(2)模拟结果与试验结果趋势相同，摩擦系数的变化对蠕变变形及稳态蠕变速率的影响与表面粗糙度的影响基本一致。

(3)在本研究范围内，不同表面粗糙度试验反演得到的蠕变应力指数n值和蠕变常数B值存在一定差异，表面粗糙度的改变会对悬臂梁小试样蠕变参数的反演产生影响。