利用压缩感知理论的声速剖面反演方法研究

张东玉，邢传玺，吴耀文

(云南民族大学 电气信息工程学院，云南 昆明 650500)

海洋拥有着丰富的资源，如矿物资源、生物资源、水资源，海洋资源的开发、利用和保护是水声学研究的最终目的，水下目标探测、导航、定位以及声呐系统性能的预测等研究成为近几年的热点，这些研究的开展都必须首先获得海洋环境参数[1].声速作为水声研究中重要的环境参数之一，是了解和研究水声信道和水声传播的基础，是所有水声学研究领域都不可缺少的重要环境参数，海洋声速剖面在声场建模和水声设备性能的评估方面占据着十分重要的地位[2].

采用直接测量的方法测量水声环境中的声速，需要多次实地测量，需要耗费大量的物力人力，相较而言，反演的方法只需一次测量就可多次重复使用，能降低成本，节省资源[3].随着水声理论日渐成熟，水声设备技术不断完善，为了更好的研究、利用和保护海洋，大量学者提出利用己有的历史声速剖面，通过反演的方法获得海洋的垂直声速剖面，最常用的方法是使用经验正交函数模型反演声速剖面，但经验正交函数模型反演声速剖面的方法容易遗漏SSP中微小扰动的特征点，同时计算效率低下，反演误差较大[5].SSP反演问题传统上是通过最小化最小二乘代价函数的解的能量来正则化，需要对复杂的SSP结构进行低采样或使用少量基函数来解释SSP的变化[6].这种分辨率的降低会导致SSP的变化不确定，当内部波或水流产生强烈的、随时间变化时，SSP的变化具有不确定性，这种不确定性会严重影响其他参数反演的准确性.

近年来，有学者开始将压缩感知理论应用于海洋声学中，如应用于波束形成，地声参数反演.压缩感知理论能够将可压缩信号在降采样观测后以很高的精度重建，打破了传统采样定理的局限.目前，压缩感知理论已经广泛应用于医学、导航、遥感等领域.文献[5]证明了CS在海洋声学中的应用，可以将重构问题可以转化为求解最小l0范数问题.在与距离无关的浅海环境中，SSP反演可以用CS来解决.在稀疏假设下，海洋中声学SSP反演可以表述为一个不确定的线性问题，在稀疏域中的SSP扰动可以用形状基函数来表示.

本文采用Kraken模型对浅海水听器的垂直线阵压力观测进行了正演模拟.用一阶泰勒展开方法对正演模型的非线性响应进行线性化[7].在稀疏域中使用形状基函数表示SSP的扰动.并用带有l1稀疏约束的最小二乘代价函数的凸优化来求解字典系数向量，最后使用CS方法反演得到SSP.实验结果表明，使用CS方法可以很好地估计SSP，并验证了CS方法对于声速剖面反演的优点.

1 基本原理

1.1 传播模型

在反演海洋环境参数的研究中，选取适当的传播模型对水声传播实验中的声场进行建模是反演研究的重要前提，反演结果的精度由传播模型的计算精度决定.从水听器的垂直线阵列(vertical line array，VLA)观察到海洋环境中的声压，然后利用简正波传播模型对海洋声场进行正向建模.简正波传播模型的基础是求解式(1)的波动方程[3].

(1)

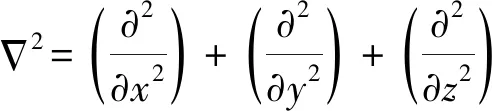
(2)

Kraken方法使用有限差分来对简正波方程进行求解，波动方程的解可以写为Φ(r)和Ψ(z)的乘积：

P(r,z)=Φ(r)Ψ(z).

(3)

将(3)式代入声压方程，可得：

(4)

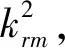
(5)

把式(5)代入式(4)可得到深度方向的模式方程如式(6)：

(6)

假设海面是绝对软边界，即，ψ(0)=0，海底为刚性边界，水深为D，满足条件：

(7)

式(7)的解有无穷多个，每一阶简正波都有对应的模态函数Ψm(z)和相应的一个水平波数krm.Ψm(z)也可叫做为本征函数，krm也可称做本征值.各阶简正波的波数都是正交的，因此有：

(8)

声压函数可由所有简正波叠加表示：

(9)

利用贝赛尔函数推导出简正波的时域声压表达式为:

(10)

水声传播信道用冲击响应h(t)来描述，信号x(t)=e-iω0t作为激励信号，用来激励信道h(t)，则相应的输出为：

y(t)=x(t)*h(t)=p(r,z)e-iω0t.

(11)

对上式进行傅里叶变换得到：

Y(ω)=X(ω)*H(ω)=2πδ(ω+ω0)p(r,z).

(12)

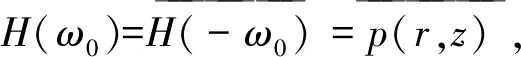
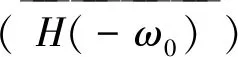
(13)

即求得信道冲击响应也即声压值P.

1.2 参数稀疏化和压缩感知

由于CS是一种寻找非定值线性系统稀疏解的技术，因此利用一阶泰勒展开对SSP的非线性响应进行线性化[7].对于k点离散化海洋SSP，c(x)∈RK建模为：

c(x)=c0+Qx,

(14)

其中，c0∈RK是使用CTD探测仪测量经转换得出的离散参考声速.Q=[q1,…,qn]∈RK×N是形状基函数qn的字典，x∈RN是字典系数向量.SSP由形状基函数建模，形状基函数描述了在x中具有少数的非零系数的SSP扰动[9].在M元VLA处接收的声压为pobs.

pobs=g(x)+n,

(15)

其中，pobs∈CM，g(x)∈CM是模型传播函数，n∈CM是高斯白噪声，声源和其他海洋环境已知.

模型传播函数的一阶泰勒展开的线性化响应为[8]：

(16)

矩阵D=[d1,…,dn]∈CK×N包含了M个压力观测值相对于字典Q中的N个形状基函数的导数.dn通过对参考剖面进行qn的一部分扰动,用双边有限差分计算.

假设dn充分非相干，利用l1范数凸优化方法找到x的稀疏估计.式(15)的稀疏解可以表示为

(17)

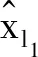
(18)

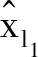
(19)

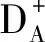
(20)

其中，λ控制解能量和度量拟合的相对重要性.

2 方法实现

使用Kraken模型对简正波声场进行仿真计算，首先编写程序提前设置好式(10)中的密度、声源距离、声源深度、接收阵元深度、衰减系数等参数，调用软件计算声场可以得到模态函数和水平波数，再把得到的相关值和参数代入求声压的式中即可得到某一频率对应的声压值.

采用Kraken模型对水深为 30 m 的海洋声场进行了数值模拟.声场由 100 Hz 的声源产生，且声源位于水下深度 10 m 处，在 1 km 范围内采样，采用M列8个均匀间隔的VLA单元，跨度6～20 m.实验参数如下：海底声速 1 700 m/s，密度 1.5 g/cm3，衰减 0.1 dB/λ.环境图如图1所示.

使用2013年在中国某海域实测的声速剖面数据作为SSP训练数据集，通过对SSP训练数据集进行主成分分析，计算出一组EOF，前3个EOF如图2所示.通过传播模型计算获得声压场的声压值，使用CS方法结合压缩估算得到的稀疏系数x对SSP进行反演.

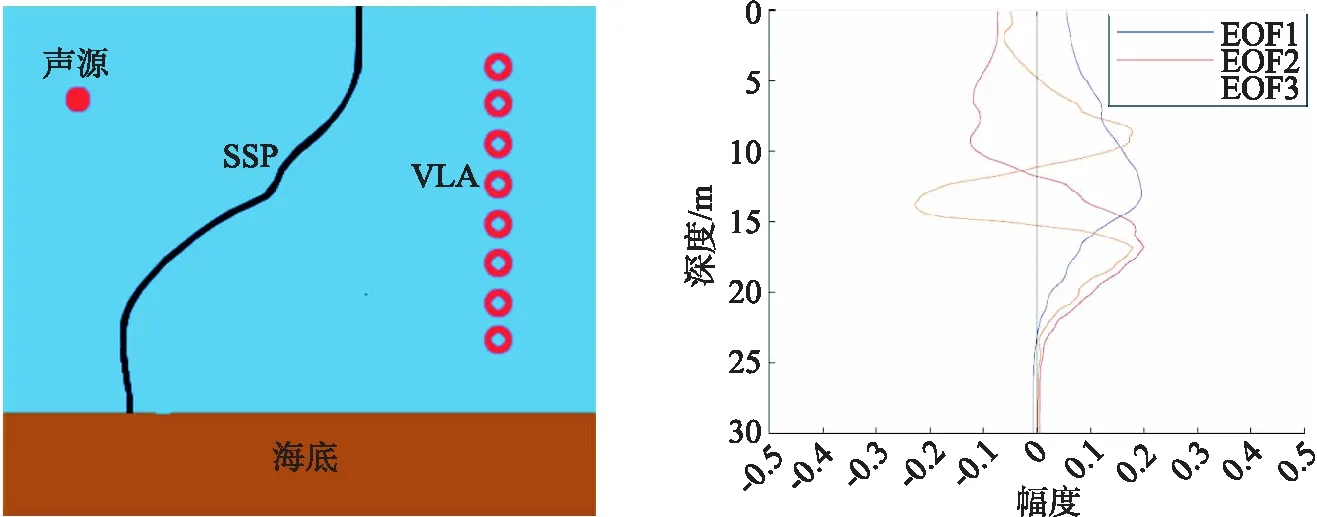
图1 实验环境图 图2 前3个EOF

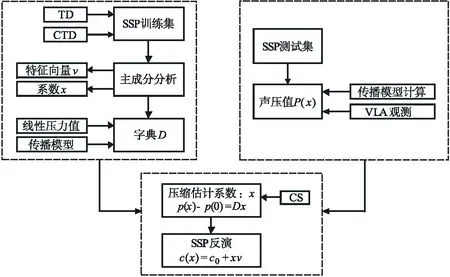
图3 SSP反演流程图

声速剖面反演步骤的过程流程图如图3所示，主要用到的声速剖面反演具体算法步骤如下：

1) 采用Kraken模型对水深 30 m 的海洋声场进行了数值模拟，得到水听器垂直阵列(VLA)中的复声压，并使用一阶泰勒展开对其进行线性化.

pobs=g(x)+n,

(21)

(22)

2) 从SSP训练集中使用数据压缩算法主成分分析(principal component analysis,PCA)方法计算得到训练集的字典系数向量X和特征向量V.

3) 离散的K个点从CTD转换得出的线性压力值离散的K个点的参考声速结合传播模型得N个离散为K个点的形状基函数qn的字典Q和M个压力观测值相对于Q中的N个形状基函数的字典D.

Q=[q1,…,qn]∈RK×N,

(23)

D=[d1,...,dn]∈CK×N.

(24)

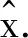
(25)

3 结果分析

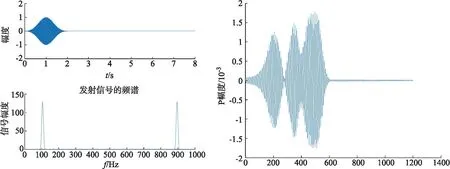
图4 发射信号 图5 水听器接收的声压

发射信号为频率 120 Hz，持续时间 2 s 的加Blackman窗进行幅度调制后的线性调频脉冲，时域信号及频谱如图4所示.图5是水听器阵列接收到的声压值P，图6是8个阵元接收到的信号，阵元接收到的信号来自同一信号，大致轮廓和信号形式是统一的，但由于阵元摆放位置不同，信号传播的路径不同，最终接收到的信号有误差.由接收信号图可以看出接收信号的时间约为 6.8 s，结合水下的平均声速 1 500 m/s，可计算得到声源水平距离在 10 000 m 附近，与 10 000 m 的声源位置一致，计算结果证明，仿真得到的水听器阵列接收到的信号的声压值可进行下一步的反演实验.

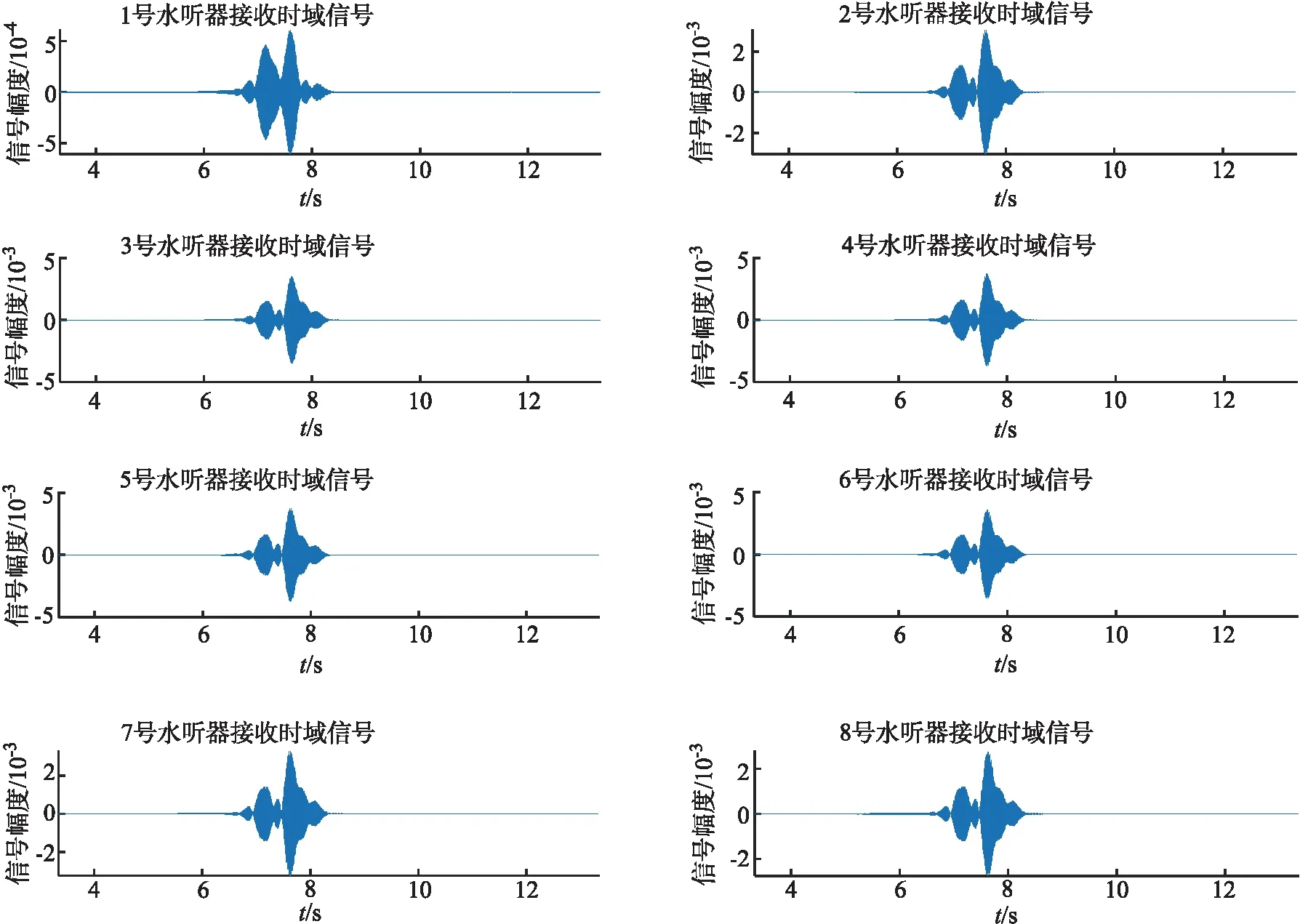
图6 8个水听器的接收信号

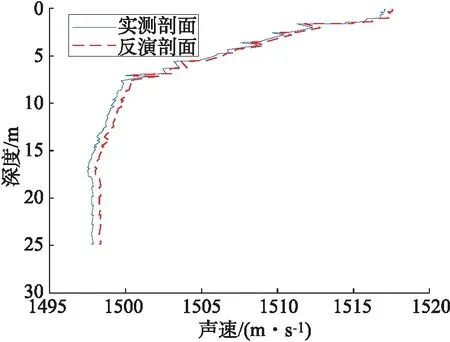
图7 声速剖面反演结果图

为了验证实验结果的可靠性和有效性，进一步验证CS方法对于声速剖面反演的优点，分析CS的性能.对图7中的实测声速剖面进行30次声速剖面计算反演过程，对最优估计值统计分析，求解获得反演声速剖面的置信区间，置信区间定义为均值±标准差的结果，近似代表置信度为70%[10-11].反演得到的声速剖面均值与测量声速剖面、置信区间与测量声速剖面对比如图8所示.

从图8看出，反演得到的声速剖面均值与实际测量的声速剖面非常接近，并且实际测量的反演声速剖面置信区间内.在30组反演计算中，得到声速剖面最大误差为 0.642 8 m/s，最小误差为 0.442 2 m/s，平均误差 0.509 5 m/s.

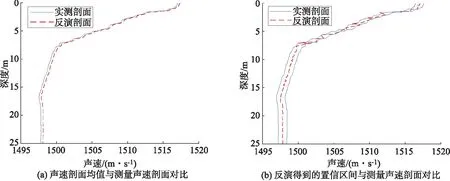
图8 反演结果对比分析

使用2013年在黄海实验的真实海试数据作为待反演声速，分别使用传统的EOF方法和本文方法进行声速剖面反演实验，反演结果图如图9所示，(a)图是使用EOF方法选前3阶经验正交函数作为基函数得到的反演剖面.(b)图使用EOF结合压缩感知方法得到的反演剖面.从图给出的2种方法的仿真结果来看，压缩感知方法的重构效果明显优于传统的EOF方法.使用压缩感知方法反演得到的声速剖面和实测的声速剖面，对 30 m 深度的 120 Hz 的单频信号的传播进行波形预报，波形预报对比图如图10所示，反演声速剖面得到的预报波形与实测声速剖面得到的预报波形基本相同，研究结果表明使用文中方法对声速进行反演是一种行之有效的方法，在水声学研究领域具有重要作用.

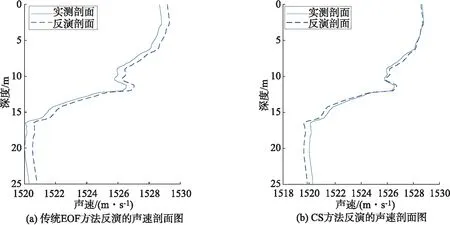
图9 反演结果对比分析

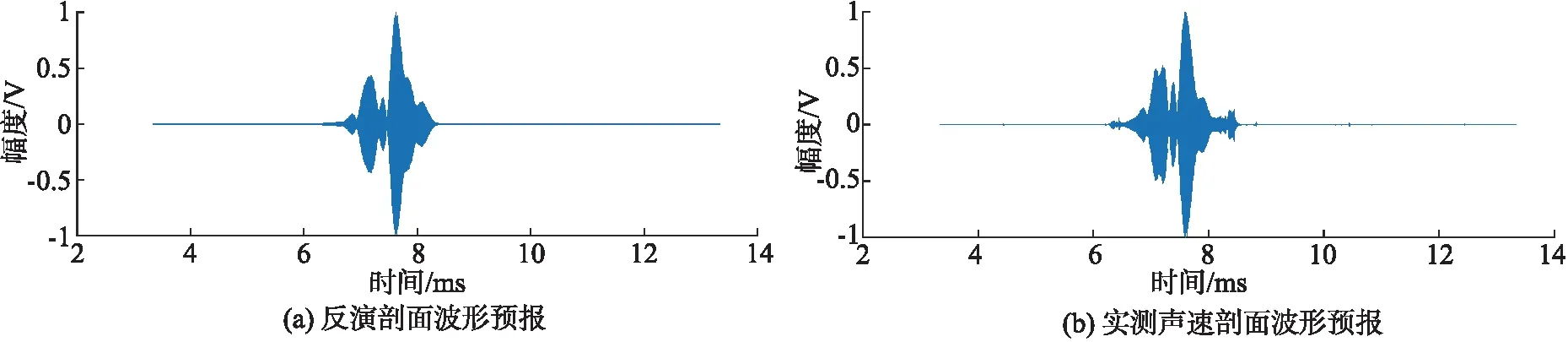
图10 波形预报对比图

4 结语

本文使用一阶泰勒展开对SSP的非线性响应进行线性化，使用海洋声速统计数据的先验知识以稀疏表示SSP的形状基函数字典，将PCA方法应用于海洋SSP数据以计算EOF，结合海洋声传播模型通过适当更新的EOF训练字典，使用l1范数凸优化方法找到稀疏估计值，结合训练字典使用CS算法对声速剖面进行反演.计算了SSP估计误差，误差的70%置信区间在 ±0.6 m/s 之内.实验结果表明，本文算法对SSP的反演是一种行之有效的方法.