管坯大变形自由推压缩径残余应力的研究

刘 恒 王连东 王晓迪 刘 超,3

1. 燕山大学车辆与能源学院，秦皇岛，066004 2. 燕山大学机械工程学院，秦皇岛，066004 3. 唐山学院交通与车辆工程系，唐山，063000

0 引言

冲压缩径是指使管坯通过锥形凹模以减小其外径的冷成形方法。按变形方式，冲压缩径可分为推压缩径、拉拔缩径；按有无芯轴，冲压缩径可分为自由缩径、芯轴缩径[1-2]。其中，自由推压缩径因具有模具结构简单、生产效率高等优势，已经广泛应用于飞机、汽车、工程机械中变径管件的制造[3]。王连东[4]采用主应力法进行了推压缩径力的求解及变形分析，认为缩径后的管坯内存在很小的应力。ZHAO等[5]建立了管材拉拔缩径的应变速度场，并基于应变速率矢量内积积分求解了拉拔力。SADOK等[6]通过有限元模拟分析了钢管缩口变形过程中的应变状态，并基于硬度测量的方法进行了实际测量，结果表明，缩径变形不均匀，有效应变的最大值出现在管坯内表面。HIRSCH等[7]的研究表明缩径变形不均匀会导致缩径后的管坯存在残余应力。GATTMAH等[8]研究了AISI 1010钢管固定芯棒拉拔残余应力，采用X射线法测量了不同断面收缩率下缩径管坯表面周向残余应力，结果表明：断面收缩率较小时，近外表面层为拉应力，近内表面层为压应力，最大周向拉应力接近140 MPa。VOLLERT等[9]采用钻孔法、Sachs法及有限元模拟法研究了中碳钢管空拔和固定芯棒拉拔残余应力，结果表明：两种拉拔方式下，管坯内表面层存在周向和轴向残余压应力，外表面层存在周向和轴向残余拉应力，并且周向和轴向残余应力均由内表面到外表面自平衡。

拉拔缩径时，由于减径后的管坯受到外部拉力的持续作用，因此拉拔缩径管坯端部不存在翘曲。而与拉拔缩径不同，自由推压缩径前管坯受到推压力作用，缩径后管坯不受外力作用，并且缩径后的管坯端部存在翘曲(端部外径大于定径区外径)[10]。对于自由推压缩径，由于推压力作用，缩径变形较大时可能导致缩径管坯失稳起皱，当单道次缩径系数(管坯缩径后外径与缩径前外径的比值)小于0.90时，即可认为该工艺为大变形自由缩径[11]。

目前国内外学者主要针对小直径管的局部缩口成形进行研究[2,12]，缩径过程中变形量较小，端部翘曲不明显。笔者所在课题组近期在进行胀压成形汽车桥壳预成形管坯的大变形缩径试验[13]时发现，缩径后管坯端部存在较大翘曲，影响制件质量，严重时甚至出现端部轴向开裂现象，于是对此现象展开研究。本文即通过理论分析，推导了端部翘曲区周向残余应力的表达式，揭示出由内表面层到外表面层整体存在周向残余拉应力；然后进行缩径试验，制备缩径管件测量试样，并采用X射线衍射法(XRD)测量内外表面层的周向和轴向残余应力；最后进行缩径有限元模拟，进一步给出自定径区至端部残余应力的分布规律。

1 端部残余应力分析

图1为管坯自由推压缩径变形简图，管坯缩径前初始直径为d0、壁厚为t0，缩径后定径区直径减至d1、壁厚增厚至t1，端部翘曲外径为d2、端部壁厚为t2。缩径凹模的半锥角为α，出口处内径为dm，锥面与出口处的过渡圆角半径为R。

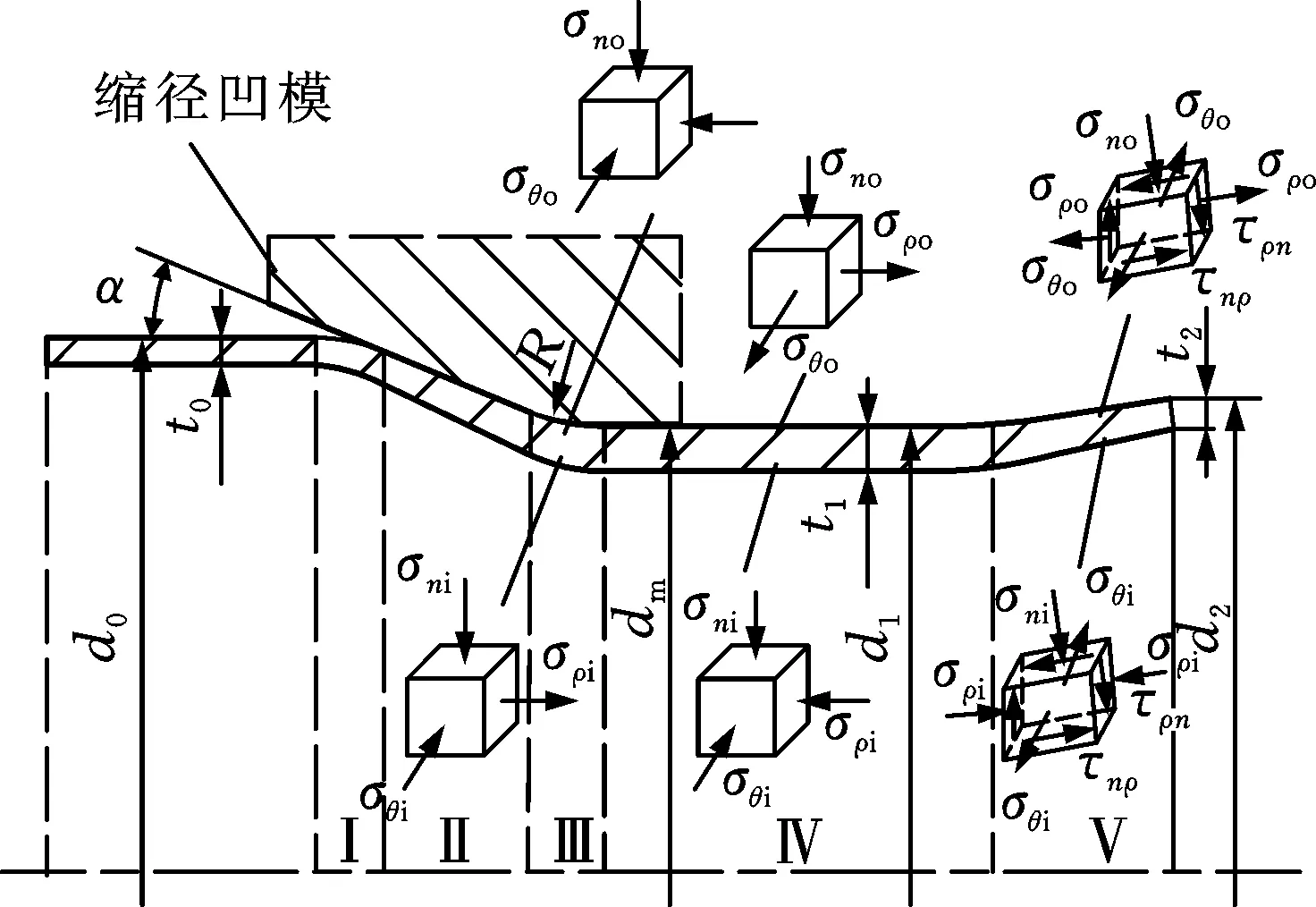
Ⅰ—入口弯曲区 Ⅱ—缩径变形区 Ⅲ—出口弯曲区 Ⅳ—定径区 Ⅴ—端部翘曲区

在缩径变形区Ⅱ，管坯减径的同时壁厚增大，该区质点单元处于三向压应力状态；在出口弯曲区Ⅲ，金属材料继续发生轴向弯曲变形，外表面层缩短、内表面层伸长。在定径区Ⅳ，金属不再受外力作用，管坯内外表面层金属沿轴向产生与弯曲变形相反的变形回弹，相当于在外表面层加上轴向拉应力，在内表面层加上轴向压应力，导致外表面层存在轴向残余拉应力σρo、内表面层存在轴向残余压应力σρi。在端部翘曲区Ⅴ，由于管坯内表面层轴向伸长大于外表面层轴向伸长[10]，端部向上翘曲，存在剪切变形，导致单元体下表面存在自左向右的剪应力τnρ，右表面存在自上向下的剪应力τρn，左表面存在自下向上的剪应力τρn。

在进行下文分析之前，给出以下基本假设：①缩径变形为轴对称变形，周向应力σθ为主应力，与周向有关的切应力分量等于零，即τθρ=τθn=0；②缩径后管坯横截面上轴向残余应力由内表面至外表面自平衡。

在端部翘曲区截取包含管坯内外表面及右端面的基元体，其左侧面为翘曲区与定径区的分界面，如图2所示。基元体周向夹角为dθ，左侧面外层周向曲率半径为d1/2、厚度为t1，上侧面轴向曲率半径为rρ、夹角为β，右侧面外层周向曲率半径为d2/2、厚度为t2。

图2 端部翘曲区基元体

基元体右侧面、上侧面、下侧面均为自由面，其上无应力；左侧面上，剪应力τρn1方向向上(由内表面层指向外表面层)，外表面层存在轴向拉应力σρo1，内表面层存在轴向压应力σρi1，其合力为零；前侧面、后侧面上仅有周向应力σθ。

根据壁厚方向上力的平衡条件，可得

2σθt1rρβsin(dθ/2)-τρn1t1(d1/2)dθcos(β/2)=0

(1)

由于dθ很小，近似取sin(dθ/2)=dθ/2，则式(1)简化后得到

由几何解析，近似取

则式(2)可变为

由式(4)可知，端部翘曲区平均周向残余应力σθ与端部翘曲变形参数和剪应力τρn1有关，且σθ与剪应力τρn1成正比。由于剪应力τρn1方向向上，故端部翘曲区周向残余应力σθ由内表面层到外表面层整体表征为残余拉应力。

2 XRD测量缩径残余应力

2.1 研究对象

自由推压缩径是一种冷成形工艺，缩径时上下夹持模固定管坯中部，左右缩径凹模分别由管坯两侧端部向内工进缩径。

针对某载重6.5 t胀压成形汽车桥壳第一道次缩径工艺，选取长度L0=1340 mm、外径d0=219 mm、壁厚t0=7.5 mm的热轧Q345B无缝钢管为初始管坯，对其两侧进行自由推压缩径。其中，缩径凹模半锥角α=23°、出口处内径dm=190 mm、过渡圆角半径R=50 mm。缩径时夹持管坯中部，保持456 mm的长度区域不变形，如图3所示。缩径系数(m=dm/d0)近似为0.87。

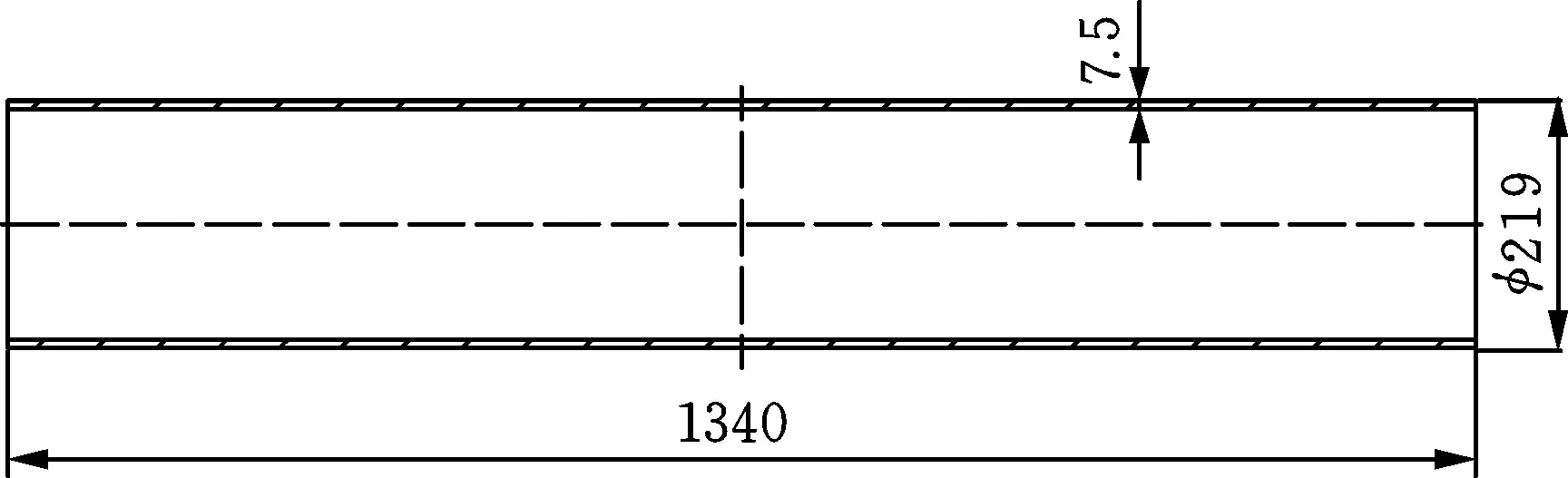
(a) 初始管坯

在室温条件下进行初始管坯样件的单向拉伸试验，得到管坯材料的真实应力-应变关系为σ=900ε0.2，屈服极限σs=362 MPa，强度极限σb=646 MPa，弹性模量E=2.1×105MPa，泊松比ν=0.3，硬化指数n=0.2，密度ρ=7800 kg/m3，延伸率δ=26%。

2.2 试样制备

在THP63-200/300/100×2型专用缩径液压机上进行管坯缩径试验，缩径模具如图4所示。上下夹持模内半径为109.5 mm，夹持宽度为250 mm。

1.左压块 2.左支撑筒 3.上模座 4.上夹持模 5.右支撑筒 6.右压块 7.右缩径凹模 8.下夹持模 9.下模座 10.左缩径凹模

缩径前对初始管坯内外表面进行除锈处理，并分别将初始管坯两侧拟缩径区域外壁、缩径凹模内壁涂抹润滑油，将初始管坯放入下夹持模并进行中心对正定位。缩径时，液压机主滑块带动上模座与上夹持模向下运动至夹持管坯中部，夹持力为450 kN；液压机左右滑块分别带动左右缩径模具以10 mm/s的速度向内工进缩径。

缩径后管件总长度为1383.32 mm，单侧伸长量为21.66 mm；定径区外径为188.28 mm，壁厚为8.42 mm；端部外径为190.08 mm，壁厚为8.16 mm，端部翘曲区长度为12.37 mm；缩径推力为1086.48 kN。

对缩径后管件采用电火花线切割加工，截取距端部长度200 mm的1/4试样，并用乙醇清洗试样。分别在试样底部的定径区、端部翘曲区内外表面选取测量点，如图5所示。定径区测量点对应截面A1-B1(点A1、B1所在截面，下同)、A2-B2、A3-B3、A4-B4、A5-B5、A6-B6，距端部距离分别为170 mm、110 mm、50 mm、25 mm、20 mm、15 mm，端部翘曲区测量点对应截面A7-B7、A8-B8、A9-B9，距端部距离分别为10 mm、5 mm、1 mm。切割面到试样底部距离大于5倍的壁厚，由圣维南原理可知，线切割对试样底部测量点的残余应力分布无影响。

图5 XRD测量点

2.3 XRD测量及结果分析

XRD是目前应用最为广泛的一种表面残余应力无损测量方法[14]，它基于X射线衍射理论和宏观弹性力学理论，通过测量多晶体晶面间距的变化来计算残余应力[15-16]。实验采用sin2ψ应力分析方法对缩径管件内外表面残余应力σφ进行测试，基本方程为

σφ=KM

(5)

式中，K为X射线应力常数；ψ为衍射晶面法线与试样表面法线的夹角；M为不同ψ角测定的2θφψ与sin2ψ直线关系的斜率；θ0为布拉格角；2θφψ为不同ψ角测定的衍射线角。

根据GB/T 7704—2017《无损检测-X射线应力测定方法》要求，采用加拿大Proto公司的iXRD型应力仪测量缩径管件试样内外表面层的周向和轴向残余应力。测量衍射晶面为{211}，靶材为CrKα，管压为20 kV，管流为4.0 mA，采用高斯拟合定峰，X射线束直径为2 mm，波长λ为0.2291 nm，曝光时间为2 s，曝光次数为6，布拉格角θ0为156.31°，ψ角取±23.69°、±17.69°、±12.41°、±11.85°、±11.28°、±6°、0°。测量周向残余应力时，试样沿轴线垂直于探测器摆动方向放置(图6a)；测量轴向残余应力时，试样沿轴线平行于探测器摆动方向放置(图6b)。

(a) 周向残余应力测量

进行水平校准、零应力标定及手动聚焦后，依次测量外表面点A1至A9、内表面点B1至B9的周向和轴向残余应力，得到相应的2θφψ-sin2ψ曲线，并经拟合计算得到测量结果。图7为测量A1点周向残余应力得到的2θφψ-sin2ψ曲线，该点周向残余应力大小为319.31 MPa，不确定度为±22.37 MPa。

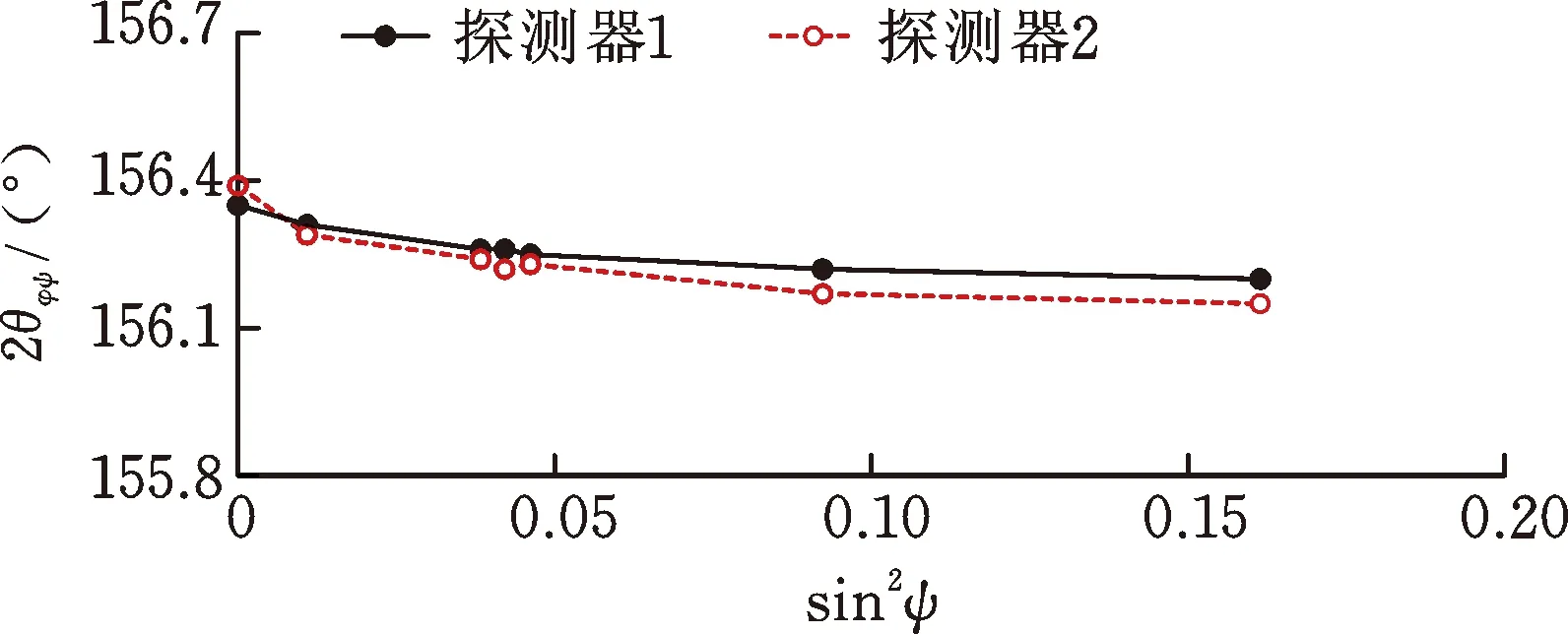
图7 2θφψ-sin2ψ关系曲线

缩径残余应力的XRD测量结果如图8所示。由测量结果可知：

图8 XRD测量结果

(1)端部翘曲区内外表面层周向残余应力均为拉应力，与理论分析的趋势一致。其中，端部A9-B9截面内表面层残余应力为520.07 MPa、外表面层残余应力为547.46 MPa，接近材料强度极限的80%。

(2)定径区外表面层存在周向和轴向拉应力，内表面层存在周向和轴向压应力。其中，周向拉应力最大值为319.31 MPa，位于A1点；周向压应力最大值为264.86 MPa，位于B2点；轴向拉应力最大值为456.16 MPa，位于A2点；轴向压应力最大值为458.31 MPa，位于B2点。

(3)由测量结果发现，定径区到端部翘曲区之间存在过渡区域，在该区域，外表面层的周向应力由拉应力逐渐变为压应力，再快速变为拉应力；内表面层的周向压应力先逐渐增大，再快速变为拉应力。该区域距离端部12.5～17.0 mm，其中A6-B6截面外层的周向压应力为82.06 MPa、内层的周向压应力为299.43 MPa。

(4)自定径区至端部，外表面层的轴向拉应力和内表面层的轴向压应力均逐渐减小，端部轴向残余应力趋近于零。

3 缩径残余应力有限元模拟

3.1 有限元模型

针对图3所示的缩径工艺，采用有限元软件ABAQUS/Standard模块隐式算法进行模拟分析。由于初始管坯、缩径凹模均属于轴对称结构，故建立1/4有限元模型，如图9所示。

图9 有限元模型

在管坯纵向中心截面施加轴对称约束,采用夹持模固定管坯中部，夹持模内径为219 mm。缩径凹模与夹持模都设定为刚体，管坯设定为变形体。管坯与模具划分网格时，网格单元类型都采用C3D8R，管坯沿壁厚方向网格单元层数为7。采用库仑摩擦模型建立夹持模与管坯间刚-柔接触模型，其接触动摩擦因数设定为0.15；缩径凹模与管坯间建立刚-柔接触，其接触动摩擦因数设定为0.10。

3.2 模拟结果及分析

3.2.1缩径变形及缩径力

表1所示为缩径管件模拟值与试验值对比，由结果可知，模拟值与试验结果基本吻合。其中端部及定径区的外径、壁厚模拟值较试验值最大相差2.21%，缩径后单侧伸长相差8.41%，缩径力相差8.21%，出现偏差的主要原因是初始管坯壁厚存在一定误差，以及润滑条件存在差别。

表1 缩径管件参数模拟值与试验值对比

3.2.2内外表面层残余应力

图10所示为内外表面层残余应力的模拟与XRD测量结果对比。由图10可知，模拟结果与测量结果的分布趋势一致，但数值大小存在一定的偏差。其中，端部A9-B9截面内表面层的周向拉应力模拟值为621.02 MPa，与测量值相差19.41%；外表面层的周向拉应力模拟值为631.03 MPa，与测量值相差15.26%。周向应力的模拟值较测量值最大相差29.63%，位于测量点A2；轴向应力模拟值与测量值最大相差28.74%，位于测量点A7。产生差值的主要原因是试样的处理及测量存在一定误差，并且有限元模拟施加的条件与试验也存在一定差别。

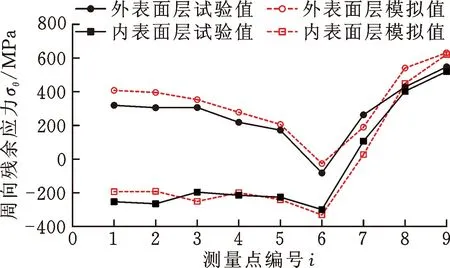
(a) 周向残余应力

3.2.3残余应力分布规律

(1)周向残余应力σθ。图11所示为周向残余应力σθ的分布结果。端部翘曲区周向拉应力由内表面层逐渐增大至外表面层。其中，端部A9-B9截面应力最大，由内表面层的621.02 MPa逐渐增大至外表面层的631.03 MPa，接近强度极限。

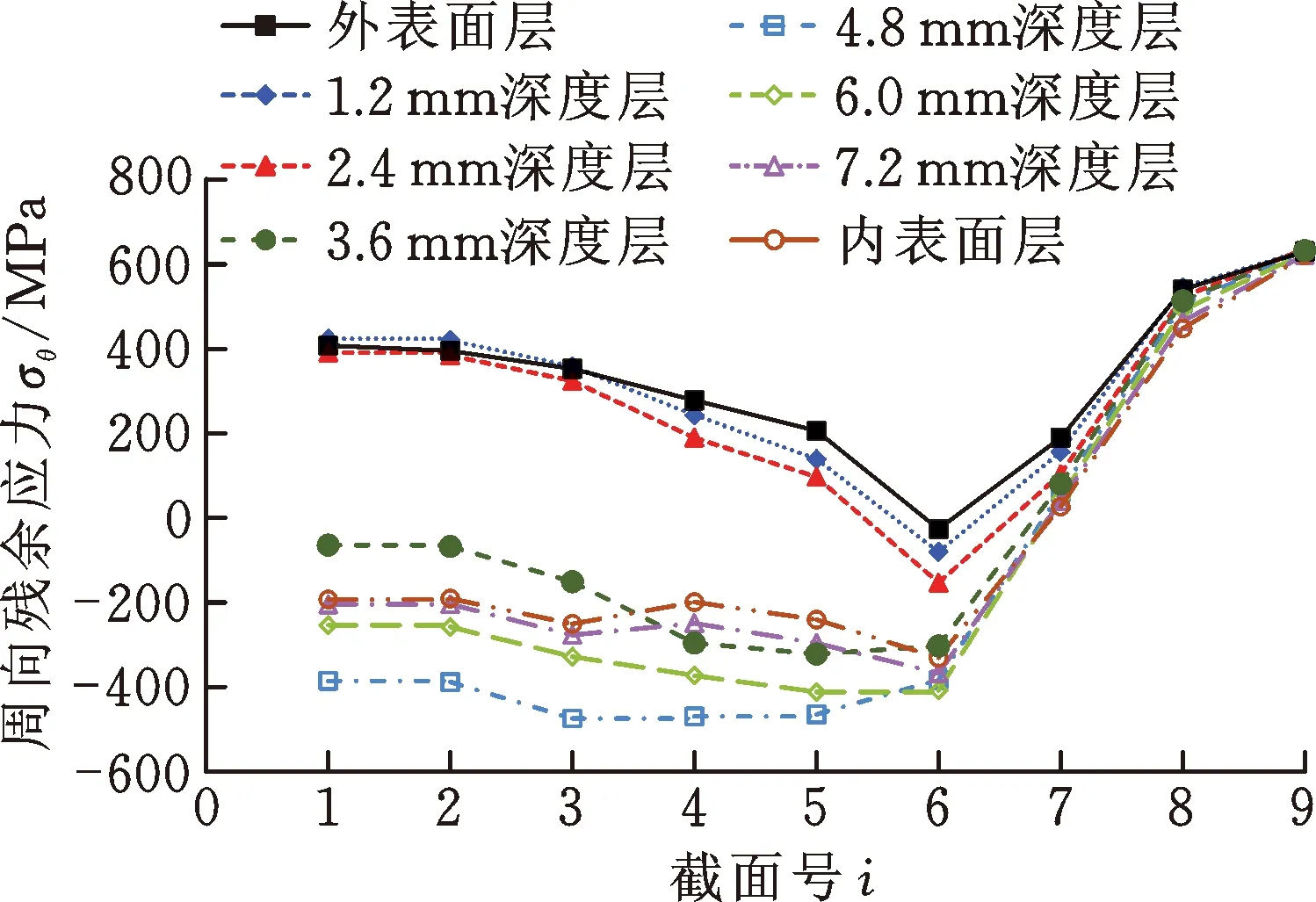
图11 周向残余应力分布

定径区周向应力由内表面层的压应力逐渐变为外表面层的拉应力。内表面层的最大压应力为250.55 MPa，外表面层的最大拉应力为407.69 MPa，在距外表面3.6 mm的深度层，压应力为64.33 MPa。

在距离端部11.5～18.0 mm的过渡区，A6-B6截面内表面层的压应力为331.03 MPa，外表面层的压应力为26.27 MPa，在距外表面3.6 mm的深度层压应力为303.14 MPa。

(2)剪切残余应力τρn。图12所示为端部翘曲区剪切残余应力τρn的分布结果。端部翘曲区的单元体右面存在方向向下(由外表面层指向内表面层)的剪应力τρn。由内表面层到外表面层，剪应力的数值先增大后减小，其中端部A9-B9截面内表面层的剪应力数值为10.47 MPa，外表面层剪应力数值为13.24 MPa，在距外表面4.8 mm的深度层剪应力数值为28.09 MPa。

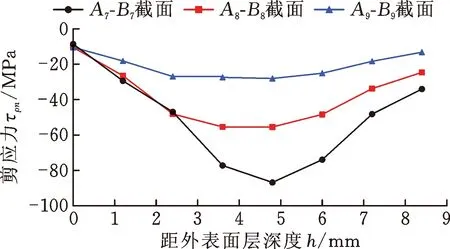
图12 端部翘曲区剪切残余应力分布

端部翘曲区的剪应力沿轴向逐渐减小，其中A7-B7截面最大剪应力为86.82 MPa，位于距外表面4.8 mm的深度层。

(3)轴向残余应力σρ。图13所示为轴向残余应力σρ的分布结果。轴向应力由内表面层的压应力逐渐变为外表面层的拉应力。定径区A1-B1截面内表面层的压应力为530.57 MPa，外表面层的拉应力为533.42 MPa；过渡区A6-B6截面内表面层的压应力为264.78 MPa，外表面层的拉应力为246.42 MPa；端部A9-B9截面内表面层的压应力为14.83 MPa，外表面层的拉应力为2.74 MPa，数值较小。由定径区到端部，各层轴向应力均逐渐减小，端部轴向应力趋近于零。

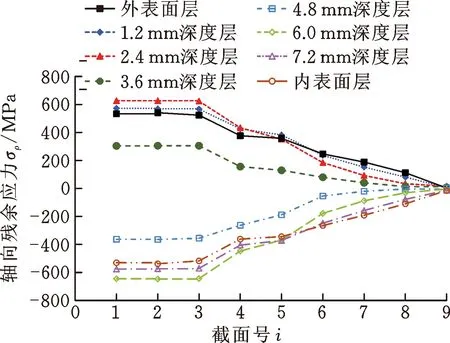
图13 轴向残余应力分布

4 结论

(1)针对大变形自由推压缩径管坯端部翘曲区，通过变形分析得出横截面上存在剪应力的结论，并推导了周向残余应力与翘曲变形和剪应力的关系表达式，揭示了由内表面层到外表面层整体存在周向残余拉应力的事实。

(2)针对φ219 mm×7.5mm无缝钢管进行了减径13%的缩径试验，采用XRD测量了缩径管件试样内外表面层残余应力，结果表明：端部翘曲区内外表面层周向应力均为拉应力，与理论分析趋势一致，且端部拉应力数值很大，内表面层为520.07 MPa、外表面层为547.46 MPa，接近材料强度极限的80%；定径区外表面层存在周向和轴向拉应力，内表面层存在周向和轴向压应力。

(3)针对缩径管件变形进行了有限元模拟，缩径变形及缩径力的模拟与缩径试验结果吻合，内外表面层残余应力的模拟与测量结果趋势一致，并揭示了端部翘曲区残余应力的分布规律：周向拉应力由内表面层逐渐增大至外表面层；剪应力由内表面层到外表面层先增大后减小；轴向应力由内表面层的压应力逐渐变为外表面层的拉应力，端部轴向应力趋近于零。

(4)由XRD测量结果发现：定径区到端部翘曲区之间存在过渡区域，在该区域，外表面层的周向应力由拉应力逐渐变为压应力，再快速变为拉应力；内表面层的周向压应力先逐渐增大再快速变为拉应力。有限元模拟结果进一步验证了该区域的应力分布规律。大变形自由推压缩径管坯端部残余应力主要与端部翘曲有关，后续将进一步研究缩径凹模的半锥角、出口直径、过渡圆角、缩径摩擦因数等工艺参数对缩径残余应力的影响，给出缩径残余应力的调控措施。