变胞四足机器人倾覆后的变胞恢复机理及其特性研究
2021-06-23王圣捷戴建生
王圣捷 戴建生,2
1. 天津大学机械工程学院,天津,300350 2. 伦敦国王学院自然科学与数学学院,伦敦,WC2R 2LS
0 引言
四足机器人作为移动机器人研究的一个重要分支,它在面对复杂地形时具有良好的适应性,因此引起了人们广泛的研究兴趣。一些具有代表性的四足机器人研究在近年来相继被提出,包括波士顿动力的BigDog[1]、麻省理工学院的Cheetah[2]和意大利理工学院的HyQ[3]等。
关于四足机器人的研究,目前主要分为结构设计、步态规划和运动控制三类。在运动控制中,机器人的稳定性研究是评价机器人运动性能的重要参数,MCGHEE等[4-5]最先提出静态稳定性三角形来计算这一指标。此后,运动稳定性三角形[6]、动态稳定性三角形[7]等指标被相继提出用来评价机器人的稳定性并指导其设计,以提高机器人的可靠性。但机器人在包含不确定因素的复杂环境中运动时,机器人的稳定性测算仍不能避免发生倾覆的情况,而当机器人发生倾覆时,往往需要人协助其恢复正常姿态。在许多情况下,例如隧道勘察、星球探测和核辐射救援等情况,人需要远距离操纵机器人,无法手动为其恢复姿态,因此,机器人具备倾覆后自我恢复的能力是十分必要的。美国宇航局(NASA)用于星球表面探测的探测车Nanorovers[8],依靠其特殊设计的轮子结构来进行自我恢复。此外,NASA也设计了一款跳跃机器人[9-11],它具备在倾覆后使机体翻转90°的自我恢复能力。HALE等[12]设计了一台依靠一个形状为三棱柱的辅助机构实现姿态恢复的跳跃机器人。李保江[13]提出了一种用于弹跳机器人倾覆后恢复姿态的恢复机构构想,从理论上对其进行了验证,使其可实现120°范围的翻转。陈殿生等[14]基于三角重心理论,提出了一种适用于机器人的翻转机构,并通过平台实验对其进行了验证。CHEN等[15]受秋叶蝉启发,设计了一种仿昆虫翅膀的机翼来使机器人自我恢复。波士顿动力的RHex机器人通过对机器人动态性能的控制,依靠动态反馈实现自我恢复[16-17]。PENG等[18]基于六足机器人,提出了一种依靠六足的协调运动实现自我恢复的方法。这些方法大致包括通过附加的机构翻转身体、依靠闭环控制使身体靠惯性摆动等,但现有的这些方法中机器人的身体都是刚性的,其翻转过程中身体并未参与运动,而自然界中动物的身体均不是刚性结构,并且在运动过程中参与了发力。在这一启发下,笔者借助变胞四足机器人[19]可动躯干的特性,在其基础上提出了一种新型的机器人倾覆后的变胞恢复策略。
1 变胞机器人概述
变胞机器人是一种以变胞机构[20]作为躯干而设计的四足机器人。变胞机构受变胞折纸[21]灵感启发,可通过机构变化[22]实现机构变自由度,从而针对不同环境做出相应变化,提高其环境适应性。变胞机构不仅能完成单一任务,还可作为一个可重构平台实现不同的功能[23]。相较于传统刚性躯干的机器人,具备可动躯干的机器人表现出了更强的地形适应性。丁希仑等[24-26]将十字交叉机构和平面六杆机构分别作为机器人的躯干,赋予其变胞特性,使其能够更好地应对横向宽窄地形的变化并采取相应的行走姿态。本文所使用的变胞机器人为依靠变胞躯干转换为多种形态来应对不同地形的四足机器人,其变胞躯干使用了由SARRUS[27]过约束结构演变而来的八杆变胞机构。通过转动和变形,这一躯干可改变为两种奇异姿态下的构型(平面构型和连续构型)。平面构型为一个具有三自由度的平面六杆机构,可在平面内实现平动。连续构型为一个具有三自由度的3R连杆机构,可实现平动与转动。基于这一特殊躯干构造,变胞机器人可实现三种不同的姿态,如图1所示。根据其关节配置方式,可分为竹节虫、蜘蛛和狗三种构型。其中,竹节虫和蜘蛛形态下躯干为平面型,狗形态下躯干为连续型。

图1 变胞机器人躯干构型与对应的三种姿态
2 变胞机器人的自我恢复过程及特性分析
2.1 机器人自我恢复的仿生灵感
对动物来说,它们发生意外而倾覆并立刻自我恢复的现象是很常见的,通过对它们自我恢复行为的观察,可以分析它们在倾覆后采取的自我恢复的策略并将其应用到机器人上。FAISAL等[28]对蝗虫倾覆后自我恢复的行为进行了研究(图2),发现当蝗虫背部着地时,它依靠左右腿的协调运动,使用两侧腿分别支撑地面和旋转身体,使身体绕其纵线转动,并依靠重心变化下落来实现翻转。这表明在躯干长宽比不为1的情况下,动物倾向于以身体纵线为旋转轴进行翻转。

图2 蝗虫的翻转过程[28]
同样地,如图3所示[29],当狗在倾覆后躺在地上并且需要翻滚时,它可以从侧面和正面两个方向进行翻滚,这两个方向是根据狗选择的旋转轴而确定的。显然,狗选择以躯干纵线为旋转轴时的力臂(lb)小于以躯干横线为旋转轴时的力臂(la)。由于躯干的质量不变,更短的力臂可以有效地减小翻转时所需的力矩,因此,动物的仿生策略可归结为动物在翻转时倾向于绕身体纵线旋转并调整重心位置借助重力翻转,这样可减少能量的消耗。

图3 狗在倾覆时的恢复策略[29]
2.2 变胞机器人的自我恢复过程
当机器人倾覆后,其身体在地面上处于翻转的姿态,由于其腿的工作空间受到限制,使其无法在地面上继续运动,要想使其恢复正常姿态,需要使其身体在竖直平面内翻转180°,重新使腿的工作空间达到地面才能使其恢复运动能力。由2.1节对动物的翻转过程分析可知,要使机器人绕身体纵线翻转,并以重心变化的位置为基础,可将这一自我恢复的翻转过程分解为三个阶段,如图4所示。状态1为初始状态,此时机器人处于倾覆状态,丧失运动能力,在这一阶段机器人需绕身体纵线翻转躯干使其恢复正常姿态;状态2为临界状态,机器人由状态1依靠腿的支撑以转动并提升躯干,使其到达临界状态,临界状态时机器人重力G方向指向旋转轴,所受重力矩为零,这一姿态下机器人达到临界平衡状态,可不依靠腿支撑来保持躯干的姿态;状态3为下落状态,在状态2后,机器人通过腿部运动来提供一个瞬时力矩以打破临界平衡状态,此时机器人可依靠重力做功继续下落直到身体完全翻转。至此,机器人的自我恢复过程完成,其躯干翻转180°后可使腿重新获得在地面上的行走能力。

图4 变胞机器人倾覆后的自我恢复过程
此外,对状态1—状态2过程进行受力分析,可近似认为质心位于机器人躯干的几何中心,不考虑腿的变化对其影响。图5所示为机器人在这一过程中某一时刻的状态,当以躯干的纵线为转动轴来翻转躯干时,将靠近旋转轴一侧的腿定义为转轴腿,远离旋转轴支撑身体的一侧腿定义为支撑腿。在机器人受重力G作用下,可以得出机器人所需的转矩Me与转轴距离d的关系:
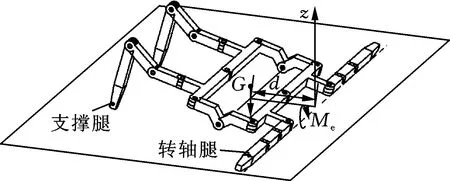
图5 状态1—状态2过程中重心与旋转轴的关系
Me=mgd
(1)
式中,Me为转动过程中所需转矩;m为机器人质量;g为重力加速度;d为机器人质心与转动轴间的水平距离。
由式(1)可知,d越小,机器人所需克服的重力矩越小。显然,当以躯干纵线为旋转轴时所需的力矩小于以横线为旋转轴时所需的力矩,这一结论也与2.1节中的动物仿生策略相吻合。
2.3 躯干无变胞的约束条件及局限性
由2.2节对自我恢复过程的分析可知,在达到状态2后,机器人只需一个微小力矩便可自由落下无需再额外做功,而从状态1—状态2过程需要机器人的腿持续做功来将躯干提升至临界状态,因此这一过程是需要重点分析的。在躯干保持刚性且姿态不变的情况下,需要依靠机器人的腿部运动来提升躯干至状态2,在这一过程中,为使躯干能够持续转动,这一转动过程在每一时刻均为静态稳定过程,因此需要支撑腿支撑并移动来提升躯干。如图6所示,在转动过程中,由于支撑腿的各部分长度和在躯干的安装位置均是固定的,因此在这些约束下,支撑腿的转动角度θab与各部分腿长的关系式为
式中,a为支撑腿的膝关节与转动轴间的距离;b为支撑腿的膝关节到足尖的长度;θab为a和b之间的夹角,且θab受机器人的关节转角限制,在变胞机器人中,其范围为80°~180°;df为支撑腿足尖到转轴的距离。
由图6可知,若想将机器人由状态1提升至状态2,b的长度可由下式求得:
由于a为定值,因此可由θab范围得到b的最小值
由这一条件不难发现,若想使机器人被提升至状态2,则在机器人设计中支撑腿的长度需满足式(4)的条件。从图6中可以看出,若需使躯干转动至状态2,机器人的支撑腿腿长将延伸至图6中达到平衡状态后的虚线处,为满足这一条件,在a的长度确定后,b的长度将大于身体长度,因此需要增大膝关节到足尖的长度,相应地机器人的腿长将会增大。通常情况下,腿长的改变会对机器人的其他性能产生影响,例如将会加长关节的负载力臂,从而会增大驱动关节的负载,这在机器人实现时会带来很大的问题。
2.4 躯干变胞的意义及恢复过程
由于在机器人躯干为刚性情况下,仅能依靠腿的自由度来进行运动,因此,在实现2.3节提到的静态支撑方法翻转机器人身体时,对支撑腿的长度有一定的要求,从而提高了对关节驱动器的要求。在变胞机器人的研究中,主要研究不同腰部形态转换与运动步态之间的协调关系,腿部的运动为研究重点,但同时也应注意到,腰部的运动也可作为主要运动来进行研究,尤其是在机器人的翻转过程中,腰部的运动将作为一个重要动作影响这一策略的实现,因此我们希望利用变胞机器人的腰部运动来解决传统刚性腰机器人在翻转时遇到的这一问题,减小对关节驱动器的要求,区别于基于躯干无变胞的恢复方式。
基于这一思路,在变胞机器人处于状态1的情况下,利用变胞八杆机构在平面构型向连续构型转化的这一运动来实现状态1—状态2这一过程,动作如图7所示。
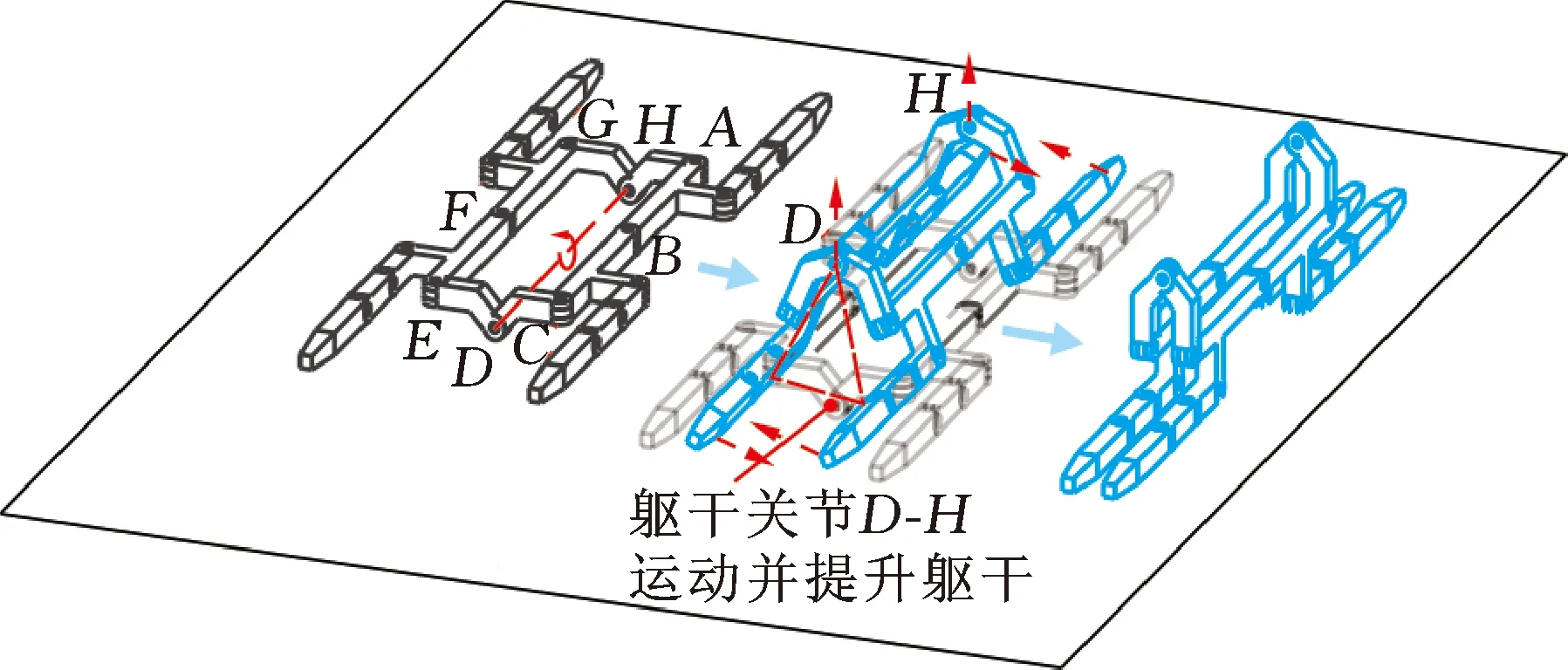
图7 变胞恢复过程的状态1—状态2阶段
为使腰部保持规则的可折叠状态,这里固定腰上的各平动关节A、B、C、E、F和G,从而使八杆机构变为一个可绕D-H转动关节转动具有一个转动自由度的二杆机构,借助腰部的转动实现变胞机器人身体被拱起的运动,当机器人达到奇异位姿时,即转变为连续构型时,可发现此时机器人姿态恰好处于状态2。与无变胞的提升躯干的方法相比,这一结合了变胞特性的方法对腿的尺寸不再有特殊的要求,而是单纯依靠躯干的转动形成了一个不断拱起躯干的运动,在这一过程中,由于机器人的姿态始终保持对称,从而可以保证重心始终位于躯干中心,躯干与地面可以在任意时刻保持稳定的等腰三角形支撑关系,大大提高了动作实现的稳定性与准确性。
在到达临界位置后,如图8所示,与无变胞的方法相似,通过一侧腿在垂直方向向地面移动来打破这一平衡状态,使机器人重心越过旋转轴并依靠重力使躯干落到地面上完成状态2—状态3阶段的转动。最后,再使躯干绕D-H转动,使机器人由连续构型变回平面构型,从而完成整个恢复动作。
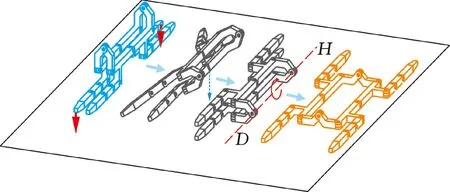
图8 变胞恢复过程的状态2—状态3阶段
2.5 变胞恢复过程的质心轨迹优化和减振原理
变胞方式的动作相比于无变胞方式的动作,除了对腿的尺寸不再有特定的要求外,还改变了躯干质心提起的高度。由图9所示的变胞方式与无变胞方式的质心轨迹的高度变化对比可以得出,变胞躯干提升至状态2的高度小于无变胞方式提升至状态2的高度。由于将这一过程看作准静态过程,因此可以给出在由状态1变为状态2时机器人所做功W与状态2时质心高度l的关系式如下:

图9 变胞方式与无变胞方式的质心轨迹
W=mg(l-h0)
(5)
式中,h0为机器人在状态1时的质心高度。
图9中,l1、l2分别对应无变胞恢复方式和变胞恢复方式达到状态2时质心的高度l。由于l2 此外,在由状态2变为状态3这一依靠重力下落的过程中,由下式的能量转化关系可求得落地时的速度vl: 求解式(6)得 由于l2 Ft=mvl (8) 式中,F为落地时机器人减速为零时所受的冲击力;t为落地时减速至零所需的时间。 由式(6)~式(8)可得 由式(9)可知,在同样的时间内,机器人的落地速度越大,受到的冲击力越大。由于变胞恢复方式时的提升高度l2 在SolidWorks中建立变胞机器人虚拟样机的三维模型,并将其导入ADAMS仿真软件中为其添加转动副约束、驱动、重力等参数,验证这一恢复策略的可行性与合理性,仿真过程如图10所示。最初,变胞机器人处于图10a所示的倾覆状态,此时即状态1的情况;然后机器人通过腰部转动将机器人躯干由平面八杆机构变为平面二杆结构,在此过程中,机器人躯干随之被拱起,直至到达状态2,达到奇异位姿的状态,转换为平面二杆结构,如图10b、图10c所示;达到状态2后,即进入了临界平衡的状态,此时机器人依靠一侧腿向下运动使变胞机器人继续旋转过一定角度,此后变胞机器人的重力不再指向旋转轴,它可依靠重力矩继续旋转,直到躯干落到地面上,如图10d、图10e所示;最后,变胞机器人再通过腰部运动,将其由连续型构型重新变回为平面构型,完成倾覆后的自我恢复,此时相较于初始情况时的机器人姿态,机器人完成了躯干的180°翻转,可重新恢复其运动能力,如图10f、图10g、图10h所示。至此,基于变胞机器人的倾覆后自我恢复动作完成。 (a) 图11为变胞恢复过程中各驱动关节的关节角度θ随时间t变化的曲线。为保持躯干由平面型构型向连续型构型转化,躯干的平动关节保持不变,转动关节在1~3 s由0°运动至180°,这一过程为由状态1到状态2的转化过程,在达到状态2过程后,支撑腿开始运动来打破状态2的临界平衡过程,在图11上支撑腿的关节运动曲线对应的时间为4~6 s。在6~8 s时,躯干依靠重力翻转到地面后,转动关节运动将躯干由连续型构型再变回平面型构型,至此,变胞恢复过程完成。 1.转动关节 2.平动关节、转轴腿各关节 3.支撑腿踝关节 4.支撑腿膝关节 5.支撑腿髋关节 图12 躯干质心的角速度-时间变化曲线 图13 躯干质心的角加速-时间变化曲线 图14为转动关节处的电机功率P随时间t变化的曲线,可得转动关节做功的过程分别为0~4 s和6~8 s的时间段,而做功的峰值为6~8 s时间段,这一过程为使用转动关节将躯干由连续型构型重新转化为平面型构型的过程,转动关节做功将一半躯干翻转180°,为主要做功部分,与图中结果吻合。 图14 转动关节的电机功率-时间变化曲线 此外,为验证2.5节中躯干变胞方式相较于躯干无变胞方式对落地时冲击力的减振作用,在仿真中对其设计了对比实验来检验这一特性,如图15所示。分别使机器人以躯干无变胞方式和变胞方式从同一位置无初始速度自由下落,其质心的速度(v)-时间(t)曲线如图16所示。 (a) 无变胞 1.变胞方式 2.无变胞方式 3.落地速度 图16为机器人由状态2到状态3过程中躯干从同一角度落到地面时,分别采用无变胞方式和变胞方式的质心速度(v)-时间(t)变化曲线,可以看出,两条曲线的速度最大值处即为躯干落地时的速度,可见在相同质量下,变胞方式落地时的速度远小于无变胞方式时躯干落地的速度。由前文的分析并结合动量定理可知,在相同时间内,速度若需减小至零,落地速度越大,其所受的外力越大,即落地所受的冲击越大,因此,通过这一仿真对比可以得出,基于变胞机器人的这一恢复动作可以有效减小机器人落地时受到的冲击力,减轻冲击对机器人机械结构及电子元器件的损伤。 3.1节在仿真环境中对变胞机器人的自我恢复过程进行了仿真及分析,然而在应用层面,还需考虑其他的因素,如地形的变化等。在不同的地形表面上进行这一动作时,机器人受到的摩擦力也随之发生变化,因此本节将对躯干拱起的过程,即由状态1向状态2变化的过程受摩擦力f的影响进行分析。首先取躯干拱起过程中的一个时刻进行受力分析,如图17所示。 图17 躯干拱起过程的受力分析 由图17可知,机器人受到的力包括摩擦力f、支持力N、重力G和转动关节的转矩Mq。对于躯干各部分的尺寸,将在竖直平面内转动关节到腿的髋关节的距离定义为lt,腿的髋关节到足尖点的垂直距离定义为lh,足部宽度的一半定义为w,转动关节到足尖点的距离定义为lr,则存在如下几何关系: 而在转动过程中,转动关节的驱动器实际上是安装在一侧躯干上以驱动另一侧躯干转动的,因此可知转矩Mq与另一侧躯干的受力情况有关,即 Mq=(Ncosβ+fsinβ)lr (11) 式中,β为lr与支持力N之间的夹角。 又由于 式中,μ为摩擦因数,受地面粗糙程度影响。 则可由式(10)和式(11)得出 式中,β为转动过程中的角度变量。 由式(13)可知,转动关节所需的驱动力矩与摩擦因数μ,尺寸参数lt、lh和w有关,且它们的增大会使得所需的力矩增大。在结构设计过程中可对尺寸参数进行控制,适当减小这几个参数即可减小转动所需的力矩。 此外,为验证摩擦因数μ对转动关节扭矩的影响,在仿真中改变地形的摩擦因数,分别取μ为0、0.1和0.2,分析转动关节扭矩Mq的变化数据,如图18所示。 1.μ=0 2.μ=0.1 3.μ=0.2 由图18可得,随着摩擦因数的增大,转动关节的扭矩Mq也随之增大,与式(13)中的结论吻合,因此在实际应用情况中,需要对地形的光滑程度进行考虑,选用扭矩合适的驱动器,从而实现这一动作。 基于变胞机器人样机,应用上述倾覆后自我恢复的策略,对机器人进行了平地上的实物验证,如图19所示。机器人通过躯干由平面型向连续型转变实现了身体拱起,达到了平衡状态,如图19a、图19b、图19c所示。随后,机器人通过腿部运动打破平衡姿态,使躯干下落至地面,随后躯干再由连续型变回为平面型,完成整个策略的执行,机器人姿态成功恢复为正常姿态,重新具备了运动能力,如图19d、图19e、图19f所示。 (a) 此外,由于这一倾覆后自我恢复的策略是基于静态平衡的条件下设计的,因此具有更好的稳定性与适应性。为验证这一特点,样机在碎石地面和草地地面也进行了实验,如图20、图21所示。相较于平面地形,碎石地面凹凸不平,机器人各部分无法保持在同一水平面内,躯干不在一个平面,增加了实现动作的难度。而草地地面摩擦力比平面摩擦力更大,会增大驱动器的负载,在翻转时受力更为复杂。但在这两种地形的测试下,机器人均完成了倾覆后的恢复,从而验证了这一策略具有一定的稳定性与适应性。 (a) 状态1 (a) 状态1 (1)基于机器人在无人环境下发生倾覆后需要自我恢复能力的需求,利用变胞机器人躯干可动这一特性,提出了一种具有静态特点的利用腰部运动完成自我恢复的策略,包括基于仿生灵感的旋转轴选取策略、基于刚性躯干下的尺寸参数约束分析和基于变胞躯干动作下的质心轨迹优化和减振能力的原理分析。 (2)设计了这一策略的具体动作,并通过仿真软件验证了其可行性。为验证其落地时对冲击力减小的作用,通过仿真对比实验测量了落地时的速度,并对两者进行了对比分析,得到了这一策略能够减缓冲击力作用的结论。为解决应用层面的问题,对不同地形下不同摩擦力的情况对驱动器的影响进行了仿真实验与数学分析,以指导在应用时驱动器的选用。 (3)利用变胞机器人样机,分别在平地、碎石地面和草地进行了实物实验,验证了该策略的可行性,并通过多种地形下的实验验证了这一基于静态特点的策略具有一定的稳定性与适应性。3 仿真实验
3.1 变胞恢复过程的仿真及分析







3.2 躯干拱起过程中驱动器转矩分析
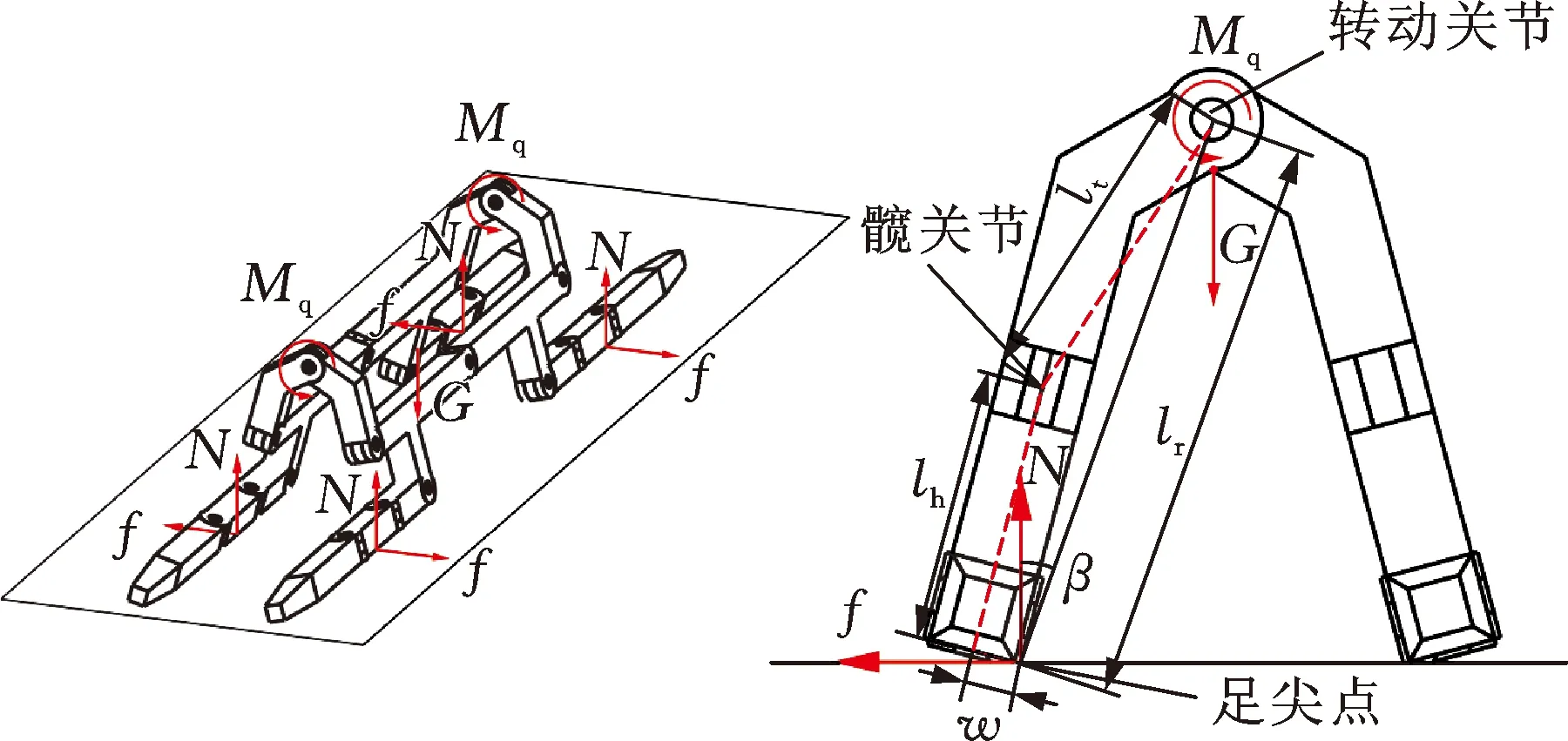

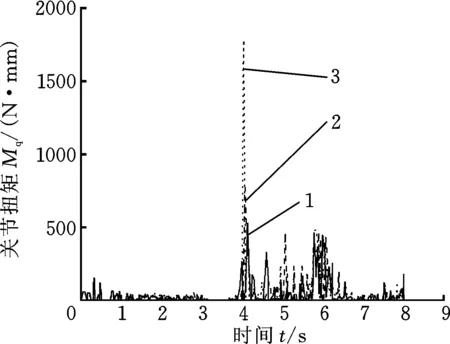
4 实物实验



5 结论
