区间直觉模糊决策方法在教学评价中的应用

朱国成，陈利群

(广东创新科技职业学院通识教育学院，广东东莞523960)

0 引言

教师的教学评价活动本质上是一种决策问题，评价途径实际上就是决策步骤的建立过程。目前有关教师教学质量评价方面的文献很多，众多学者从不同维度，利用不同方法对该问题进行了深入研究并取得了大量研究成果。例如，文献[1]从教学态度、内容、管理、基本功、方法、效果等6个维度出发构建评价指标，指标权重利用层次分析法计算，并采用统计方法构建了教师教学评价模型，取得了理想的评价效果;在高校教师教学质量评价方面，文献[2]从教师自我评价、定性与定量评价相结合的角度出发，构建多元化评价主体理论;文献[3]基于胜任力模型，指出了教学评价质量观转型方向，解决了阻碍教学质量提升的几个问题;文献[4]利用模糊综合评价方法对高校教师教学质量进行综合评价，该方法的优点是可操作性强，效果较好；缺点是评价过程中容易丢失决策信息;文献[5]以无机化学实验课程单科教学为例，从量化差异分析入手，对课堂教学效果进行了研究分析;文献[6]以加德纳多元智能理论为基础对高校英语语音课堂构建了多元化的评价体系;文献[7]从培养学生学习能力角度出发，对高等数学课堂教学进行了新的评价定位;文献[8，9]利用区间相关理论，通过对各参评教师的加权评教因素的优劣个数进行比对以达到决策目的，在没有绝对权威评教因素的情况下，该方法真实可靠;文献[10]讨论了督导专家权重在4种情形下的计算方法，并在此基础上构建了一整套对教师教学质量进行评价的模糊决策方法;文献[11]针对非权威的评教因素分数进行了模糊化处理，将经典的教师教学评价问题转化成在模糊环境下解决的问题。

在前人取得的教师教学质量评价问题的成果中，一般要讨论两种情境:一是在得到的教学质量评价数据为精确数值的确定情形下，教学质量评价问题就是经典多属性群决策问题;二是将由不确定信息条件下得到的教学质量评价数据构成的评价问题转换为模糊环境下的多属性群决策问题。第一种做法的优点是教学评价数据不难获取，评价模型容易构建，同时该做法比较符合人的思维方式，所以在不确定信息理论没有出现之前一般都采用该做法。但是，由于该方法忽略了人的思维的不确定性以及评价环境因素的模糊性，其自身存在的缺点也显而易见，故最终的评价结果往往“难以服众”。第二种做法的优点是克服了第一种做法的缺点，但第一种做法的优点又转变成为了第二种做法的缺点。例如，在获取教学评价数据时，人们比较擅长给出具体数值或者评价术语，对于不确定信息数据的给出随意性较大。事实上，不确定信息数据反映的是人的主观愿望，是对精确数据的另外一种表达方法，具有严密的逻辑性。遗憾的是目前将精确数据通过数学模型转化为不确定性数据的见刊文献较少，文献[8，10，11]在此方面进行了有益探索。

在文献[10，11]的方法基础上，课题组建立了将精确评价数据转化为区间直觉模糊数的新的数学模型，重新定义了基于方案权系数的描述函数及区间直觉模糊数的排序方法，将高职理论课堂教师教学评价这一经典多属性群决策问题转换为区间直觉模糊环境下的多属性群决策问题。该方法克服了前文提到的2种情形的缺点，为教师课堂教学水平评价提供了一种新的解决方法。

1 预备知识

定义1 设非空集合X，有如下表达形式:A={〈x，μA(x)，vA(x)〉|x∈X}，μA(x)、vA(x)分别表示集合X中元素x属于A的隶属度及非隶属度，若对于∀x∈X满足如下条件:

(1)μA(x)，vA(x)∈[0，1];(2)0≤μA(x)+vA(x)≤1，则称A={(〈x，μA(x)，vA(x)〉|x∈X}为直觉模糊集合，简称直觉模糊集。当μA(x)，vA(x)为包含在[0，1]中的区间数且二者区间数上确界之和小于等于1，则称A={(〈x，μA(x)，vA(x)〉|x∈X}为区间上的直觉模糊集合，简称区间直觉模糊集。

(1)

(2)

式中，ω为对应方案的权重，表示方案的重要程度。

2 属性权重的确定方法

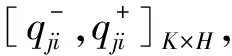
式中：min{qlji}指专家组给予方案Pj中属性Gi的最小分值；max{qlji}指专家组给予方案Pj中属性Gi的最大分值。

根据本课题组构造区间数路径及文献[12]计算权重的方法，计算步骤如下:

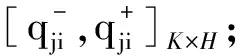
(3)采用文献[12]方法计算属性权重ωGi(i=1，2，…，H)。

3 模糊化属性值及群决策步骤的构建

第1步 利用本文思路计算属性权重ωGi;

(3)

(4)

(5)

(6)

(7)

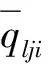
性质1表明:属性的综合得分值越大，区间直觉模糊数中关于属性好的隶属度越高，非隶属度越低，说明在转化过程中数据完美保留了原有信息动态，故可以使用模型(4)～(7)进行转化。

性质2 所有方案对应的同一属性分数为满分或零分，转化后的区间直觉模糊数分别为([1，1]，[0，0])，([0，0]，[1，1])。

证明:由熵值法计算属性权重可知，若属性分值为满分或零分，则其对应权重为0，将其带入式(4)～(7)即得。

显然，性质2为定义6的特例。

第6步 利用式(2)计算f(Pj)得F(Pj)，j∈{1，2，…，K};

第7步 根据F(Pj)，j∈{1，2，…，K}大小对方案进行排序，大者为优。

第8步 结束。

4 案例分析

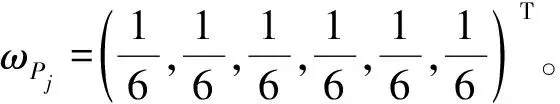
表1 教学督导评教表

表2 评教属性说明

4.1 专家评分矩阵的转换

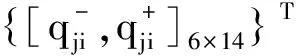
参照文献[12]区间数熵值法计算评教属性Gi权重ωGi：

4.2 模糊化评学属性值

([0.750 3，0.850 0]，[0.012 4，0.021 8])([0.820 4，0.887 9]，[0.005 3，0.008 9])([0.848 7，0.931 0]，[0.003 8，0.008 7])

([0.749 8，0.844 3]，[0.012 5，0.022 4])([0.741 9，0.803 1]，[0.009 8，0.013 3])([0.861 0，0.938 2]，[0.003 5，0.008 0])

([0.774 4，0.877 4]，[0.010 0，0.019 3])([0.699 0，0.756 7]，[0.012 4，0.016 0])([0.838 6，0.920 0]，[0.004 4，0.009 4])

([0.771 2，0.873 8]，[0.010 2，0.019 6])([0.744 5，0.806 0]，[0.009 7，0.013 1])([0.831 3，0.912 0]，[0.004 9，0.009 9])

([0.701 1，0.794 3]，[0.017 5，0.026 8])([0.706 1，0.764 4]，[0.012 0，0.015 5])([0.842 4，0.924 2]，[0.004 2，0.009 1])

([0.706 1，0.800 0]，[0.016 9，0.026 2])([0.694 2，0.751 4]，[0.012 7，0.016 2])([0.826 0，0.906 2]，[0.005 2，0.010 2])

([0.782 3，0.941 1]，[0.007 6，0.030 5])([0.830 1，0.916 8]，[0.005 1，0.010 7])([0.675 6，0.911 6]，[0.023 9，0.098 0])

([0.820 8，0.987 7]，[0.001 5，0.024 6])([0.870 6，0.961 7]，[0.002 3，0.008 0])([0.633 5，0.854 8]，[0.040 3，0.113 2])

([0.787 2，0.947 2]，[0.006 8，0.029 8])([0.819 0，0.904 6]，[0.005 8，0.011 6])([0.674 5，0.910 0]，[0.024 3，0.098 4])

([0.842 6，0.978 6]，[0.002 4，0.021 4])([0.771 7，0.852 4]，[0.009 3，0.015 0])([0.680 6，0.918 4]，[0.022 0，0.096 2])

([0.828 1，0.996 4]，[0.000 4，0.023 6])([0.820 6，0.906 4]，[0.005 7，0.011 5])([0.672 7，0.907 7]，[0.025 0，0.099 0])

([0.841 6，0.978 5]，[0.002 4，0.021 5])([0.821 4，0.907 2]，[0.005 7，0.011 4])([0.660 7，0.891 4]，[0.029 6，0.103 3])

([0.720 7，0.816 7]，[0.015 4，0.024 9])([0.736 2，0.987 1]，[0.009 8，0.012 9])([0.829 3，0.973 9]，[0.004 3，0.029 8])

([0.721 3，0.817 5]，[0.015 4，0.024 8])([0.716 5，0.986 0]，[0.010 9，0.014 0])([0.835 8，0.974 9]，[0.004 1，0.028 6])

([0.673 8，0.763 6]，[0.020 5，0.029 9])([0.718 7，0.774 9]，[0.010 7，0.013 9])([0.803 5，0.969 5]，[0.005 0，0.034 8])

([0.672 7，0.762 5]，[0.020 6，0.030 0])([0.774 3，0.989 2]，[0.007 6，0.010 8])([0.828 0，0.973 7]，[0.004 3，0.030 0])

([0.754 4，0.855 1]，[0.012 0，0.021 3])([0.714 2，0.770 1]，[0.011 0，0.014 1])([0.770 3，0.960 4]，[0.006 5，0.041 3])

([0.758 3，0.859 5]，[0.011 5，0.021 0])([0.721 6，0.778 2]，[0.010 6，0.013 7])([0.774 7，0.965 9]，[0.005 6，0.040 4])

4.3 融合属性模糊数据

f(P1)=([0.755 0，0.890 2]，[0.011 9，0.035 7])，f(P2)=([0.758 4，0.892 7]，[0.013 7，0.037 1]);

f(P3)=([0.754 9，0.887 4]，[0.011 6，0.035 8])，f(P4)=([0.769 1，0.902 1]，[0.010 1，0.033 3]);

f(P5)=([0.761 3，0.896 7]，[0.010 6，0.035 7])，f(P6)=([0.746 2，0.876 0]，[0.012 8，0.038 6])。

利用式(2)对f(Pj)进行计算得出综合属性评价结果:

F(P1)=0.255 4，F(P2)=0.256 1，F(P3)=0.254 6，F(P4)=0.265 6，F(P5)=0.260 1，F(P6)=0.242 8。

显然有F(P4)>F(P5)>F(P2)>F(P1)>F(P3)>F(P6)。督导组对6位教师教学评比结果为:第4位教师教学水平最强，第6位教师教学水平最弱。

课题组对评教属性信息数据进行了模糊化处理，大幅压缩了教师评分数据，评价结果更容易被教师认可。同时，由于在处理过程中考虑了督导的重要性、评教属性的重要性，使整个决策过程比较科学。

5 结语

针对教师教学评教属性权重未知，而评教属性值为确定数的教师教学水平评教构成的多属性群决策问题，提出了一种将评价专家给出的评教属性值转换为区间数的方法，进而利用区间数熵值法确定属性权重，其赋权方法为组合赋权法。本文构建的方法既考虑了专家打分的主观性，又利用了区间数模型计算权重，具有较严密的数学理论依据，可较客观地对评教属性进行赋权。本文探索了将督导专家组给出的对同一位教师评教属性值转化为区间直觉模糊数的一种路径，并用新定义的区间直觉模糊数排序方法进行评价。该方法从模糊干预的角度出发，丰富了多属性群决策理论相关知识。