基于贝叶斯网的开放世界知识图谱补全
2021-06-18李鑫柏吴鑫然
李鑫柏,吴鑫然,岳 昆
(云南大学 信息学院,昆明 650500)
0 概述
知识图谱(Knowledge Graph,KG)是海量数据领域中重要的知识储备库[1-2],为知识查询、问答系统和推荐系统[3]等应用提供知识服务[4-5]。KG 用节点表示实体,用边表示实体间的关系,一个由关系、头实体和尾实体构成的三元组表示一个事实。知识图谱补全(Knowledge Graph Completion,KGC)指通过预测实体之间的新关系来构造三元组[6],从而提升KG 中知识的丰富程度[7]。
将实体和关系表示为低维空间中的向量,是一类有效的KGC 方法,通过向量间的计算来解决KG内部的关系预测问题。但现实世界中的知识在不断增加变化,这要求KG 及时补充现实世界中的知识,而这类KGC 方法难以满足从现实世界中学习知识的要求。因此,研究人员将KG 内部的补全方法称为封闭世界下的KGC 方法,将不包含于KG 的数据称为开放世界数据,进一步提出开放世界KGC 方法,这类方法的基本思想是从数据中提取KG 中不存在的新实体来补全三元组,从而为KG 引入新实体。
现有的开放世界KGC 方法虽然有效地解决了新实体的来源问题,但每次只能针对缺失头实体或尾实体的一个三元组进行补全,在一定程度上限制了新知识的全面性。KG 中关系之间存在相互依赖的性质,可以用来学习新实体的多种关系,但KG 不能直接描述这种依赖性。贝叶斯网(Bayesian Network,BN)是表示和推理具有依赖性和不确定性知识的有效工具。本文提出一种基于BN 的开放世界KGC 方法,给出关系之间依赖性的BN 表示模型,设计BN模型构建方法,利用KG 来构建BN。在此基础上,提出基于BN 概率推理的三元组构造方法,利用现有的命名实体识别技术从开放世界数据中获取包含新实体的三元组,将其作为证据,基于BN 概率推理构造更多包含新实体的三元组,从而提升知识的全面性并完善KG。
1 相关工作
基于KG 的表示学习进行KGC 是一类典型的KGC 方法,其补全效果的好坏依赖于表示模型的性能高低。TransE 模型[8]将关系视为实体间的平移向量,其能够有效计算“一对一”关系,但计算“一对多”“多对一”和“多对多”等复杂关系时存在局限性。文献[9]提出TransH 模型,利用超平面及该超平面上的向量表示关系,使每个实体在不同关系下拥有不同的向量表示,但TransH 仍假设实体和关系处于相同的语义空间,在一定程度上限制了其表示能力[10]。文献[11]提出TransR 模型,为实体向量构造一个公共的空间,并为每个关系向量构造只属于该关系的空间。
上述方法能够将KG 中的实体和关系表示为向量空间中的向量,不仅保存了实体和关系的语义,还使得实体和关系变得可计算,进而为KGC、KG 查询等任务提供定量的依据,对KG 具有重要意义。虽然基于表示学习的封闭世界KGC 方法能够在KG 内部有效地预测三元组,但是开放世界中的新知识也是补全KG 的重要知识来源。封闭世界KGC 方法难以满足向KG 中引入新实体的要求,因此,有必要研究开放世界KGC 方法。
近年来,研究人员用开放世界KGC 方法从数据中提取新实体加入KG,从而丰富KG 中的知识。文献[12]利用全卷积神经网络从数据中提取新实体,进而利用新实体补全缺失头实体或尾实体的三元组,为KGC 提供了一种新思路。文献[13]将文本、图片和数值等多种类型数据作为新实体来构造三元组,丰富了KG 中实体的类型,但多种类型的数据导致计算复杂度较高。
开放世界KGC 方法能够为KG 引入开放世界中的新实体,为KGC 方法提供一种新思路。现有的开放世界KGC 方法依赖于数据中给出的知识,能够学习到数据中直接描述出的与新实体相关的知识。然而,与一个实体相关的知识往往是多方面的,数据中给出的知识通常只是其中的一部分。现有的开放世界KGC 方法虽然能够引入新实体,但无法提升知识的全面性。若利用开放世界数据中给出的知识学习到更多知识,同时对新实体所涉及的多种关系进行补全,将大幅提高新知识的全面性和KGC 的效率。
2 基于KGBN 的知识图谱补全
KG 中同一类型实体涉及的关系之间通常具有相互依赖的性质,给定某个类型实体涉及的一些关系,通过关系之间的依赖性可得到该实体可能涉及的其他关系,从而利用该实体及更多关系来构造三元组。若从开放世界数据中提取的新实体与KG 中的实体为相同类型,则新实体涉及的关系往往也符合KG 中关系之间的相关性。例如,一部电影的类型为“喜剧”,另一部电影与这部电影具有相同的导演,则其类型很可能也为“喜剧”。在开放世界KGC 任务中利用这种依赖性,能基于数据中新实体给定的关系获取其涉及的更多关系,从而提升KG 中知识的全面性。因此,如何定量地描述KG 中同类实体涉及的关系之间的依赖性,是实现开放世界KGC 的重要前提。
BN[14]是描述变量间相互依赖关系和不确定性知识的有效工具[15]。基于证据变量的取值,利用BN 的概率推理,可计算得到查询变量不同取值的条件概率。鉴于BN对不确定性知识表示与推理的优势,本文将BN作为KG 中关系之间依赖性表示和推理的框架,构建一个基于KG的BN(KG-based Bayesian Network,KGBN),其中包含有向无环图(Directed Acyclic Graph,DAG)和条件概率表(Conditional Probability Table,CPT),将KG中的关系表示为KGBN 中的变量,并将KG 中关系连接的不同尾实体表示为KGBN 中变量的不同取值。如图1 所示,将KG 中的关系“导演”“演员”和“类型”表示为KGBN 中的变量x1、x2和x3“,演员1”出演的某部电影为“喜剧”的可能性可利用条件概率P(x3=“喜剧”|x2=“演员1”)=0.95 进行定量描述。

图1 KGBN 示例Fig.1 Example of KGBN
KGBN 的构建包括DAG 构建和CPT 计算。对于同一类型的实体而言,它们共同涉及的关系描述了该类实体的特性,在KGC 任务中考虑这些关系对实体的描述作用,能够更准确地获取新实体的特性,从而为构造三元组提供可靠的依据。因此,本文将关系在实体描述中的重要程度作为构建DAG 的依据,在DAG 中使得重要关系的优先级高于次要关系,进而获取关系之间的依赖性。具体而言,关系的出现频率越低,则越能准确描述实体的特点[16]。若将关系看作一种“资源”,关系连接的尾实体看作“传播介质”[17],那么“传递资源多”的关系在实体描述中发挥着更重要的作用,如“语言”关系的尾实体“普通话”一般不具备其他信息,而“导演”关系的尾实体“导演1”具有国籍、作品等信息,根据“导演1”容易推出电影的“语言”为“普通话”,反之则很难推出一部“普通话”电影的“导演”是“导演1”。
本文提出基于KG 中关系出现频率和传递资源数的DAG 构建方法,给出关系在实体描述中重要程度的定量计算方法,将一个关系重要于另一个关系的状态表示为DAG 中一个变量指向另一个变量的有向边,构造出DAG,进而提出基于KG 的三元组数据集抽取方法,从KG 中抽取关系与尾实体的不同组合情况,并获取每种组合的出现次数,从而得到包含KGBN 中不同变量取值组合及其个数的数据集。在此基础上,给出基于最大似然估计法的CPT 计算方法,利用DAG 和数据集为每个变量计算CPT,最终构建出KGBN。
为了实现开放世界KGC,本文将从开放世界数据中提取的包含新实体的三元组作为KGBN 推理的证据,通过概率推理来获取新实体涉及的更多关系,从而构造出新的三元组。BN 推理分为精确推理和近似推理,精确推理通过给定证据变量取值来计算查询变量的后验概率分布,近似推理降低了精确推理的复杂度和对精度的要求,以在较短时间内得到一个近似解[18]。
三元组的正确与否决定了KG 所表达知识的可靠性,考虑到KGC 任务对结果的精度要求较高,本文在KGBN 推理中采用精确推理,提出基于KGBN推理的三元组构造方法,从数据中提取包含新实体的三元组,将其中的关系及尾实体作为KGBN 推理中的证据变量及其取值,并将KGBN 中其他未知取值的变量作为查询变量,进而基于KGBN 推理得到查询变量不同取值的条件概率,将条件概率作为构造新三元组的依据,从而构造出包含新实体及更多关系的三元组。
本文方法也可用于封闭世界KGC 任务,即针对KG 中已有的实体进行补全。针对KG 中已有的某个实体,在包含该实体的三元组中存在已知的关系和尾实体,可以作为KGBN 推理的证据变量及其取值,基于KGBN 推理即可获取其他变量的取值条件概率,进而构造出更多三元组。
本文使用DBpedia数据集[19]和Freebase数据集[20],分别在开放世界和封闭世界下进行链路预测和三元组类型预测实验,以测试本文方法的结构构建效率。
3 KGBN 构建
3.1 相关定义
定 义1[10]将KG 表示为GK=(E,R,T),其中,E={e1,e2,…,eε}表示实体集合,ε为实体个数,R={r1,r2,…,rγ}表示关系集合,γ为关系的个数,T={(h,r,t)}(h,t∊E,h≠t,r∊R)表示三元组集合,h为头实体,t为尾实体。
BN 通过DAG 和CPT 来表示和推理变量间的相互依赖关系和不确定性知识,其中,DAG 的节点表示变量,有向边表示变量间的依赖关系,每个节点具有一个CPT,描述了父节点对该节点的影响程度。KGBN 由DAG 和CPT 构成,其中,变量表示KG 中的关系,变量的取值表示关系连接的尾实体。为方便后续讨论,将KGBN 中的变量个数设为n(n<γ)。
定义2将KGBN 表示为φ=(GB,θ),其中:
1)GB=(X,Y)表示DAG 结构,X={x1,x2,…,xn}表示变量集,xi表示GK中同类实体所涉及的任意一个关系,Y表示有向边集,表示由xi到xj的有向边,此时,xi称为xj的父变量,变量xj的父变量集合记为Ppa(xj)。
2)θ表示所有变量 的CPT 集合,其由P(xi)和P(xi|Ppa(xi))构成。
3.2 DAG 构建
为了构建KGBN,本文提出基于关系出现次数和传递资源数的DAG 构建方法,通过定量计算关系在实体描述中的重要程度来获取关系之间的优先级别,并将其表示为DAG 中变量之间的有向边,从而获取KG中同一类型实体所涉及的关系之间的依赖性。
KG 中出现频率低的关系能更准确地描述实体的特点,例如,某部电影具有2 位“主演”和10 位“工作人员”,“主演”往往比“工作人员”更能说明电影的特点。本文提出逆频(Inverse Frequency,IF)指标来度量关系在实体描述中的重要程度。对于GK中的任意关系r,IF 计算公式如下:

其中,NT(r)为三元组集合T中包含关系r的三元组个数。
KG 中“传递资源越多”的关系对实体描述的作用越大,本文提出关系传递(Relation Transfer,RT)指标,在某些关系具有相同IF 值时,利用RT 值度量这些关系对实体描述的重要程度。对于r,RT 计算公式如下:

其中,Er表示在集合T中关系r连接的尾实体集合,NT(h∊Er)表示集合T中以Er中各实体为头实体的三元组个数,即关系r连接的尾实体的出度之和为φ中n个变量所表示的关系的NT(h∊Er)之和。
在构建GB时,首先利用式(1)计算各变量所表示关系的IF 值,并根据IF 值对变量进行降序排列,得到GB的变量集X和关系的IF 值数组;然后统计关系在GK中传递的资源数,利用式(2)计算X中各变量所表示关系的RT 值,得到关系的RT 值数组。
在进行DAG 构建时,依次从变量集X中取出变量xi(1≤i≤n-1),放入SameX集合中,并将这个变量所表示关系的IF 值与X中下一个变量xi+1(1≤i≤n-1)所表示关系的IF 值进行比较,比较结果分为以下4 种情况:
1)若两个关系的IF 值不相等,则在有向边集Y中添加SameX集中每个变量指向下一个变量xi+1的有向边。
2)若两个关系的IF 值相等,进而比较它们的RT值,并在Y中添加所表示关系的RT 值大的变量指向所表示关系的RT 值小的变量的有向边。
3)若两个关系的IF 值和RT 值均相等,则判断这个变量是否为X中的倒数第二个变量,若不是,则将这个变量保留在SameX集中,并开始下一次循环,因此,SameX集中的变量所表示的关系的IF 值和RT 值总是相等的。
4)若两个关系的IF 值和RT 值均相等,且这个变量xi是X中的倒数第二个变量,则将X中的最后一个变量xn放入SameX集,并获取SameX集中的变量个数s,找到X中第n−s个变量xn-s,xn-s即为所表示关系的RT 值大于SameX集中变量所表示关系的RT 值的最接近的变量,接着在Y中分别添加xn-s指向SameX集中除第一个变量之外的每个变量的有向边,并清空SameX集,结束循环。
DAG 的构建过程如算法1 所示:
算法1KGBN 的DAG 构建

算法1 的执行代价主要取决于KGBN 中变量的个数,若变量集X中有n个变量,则算法1 的时间复杂度为O(n)。
如表1 所示,算法1 在第一次、第二次执行中分别添加有向边
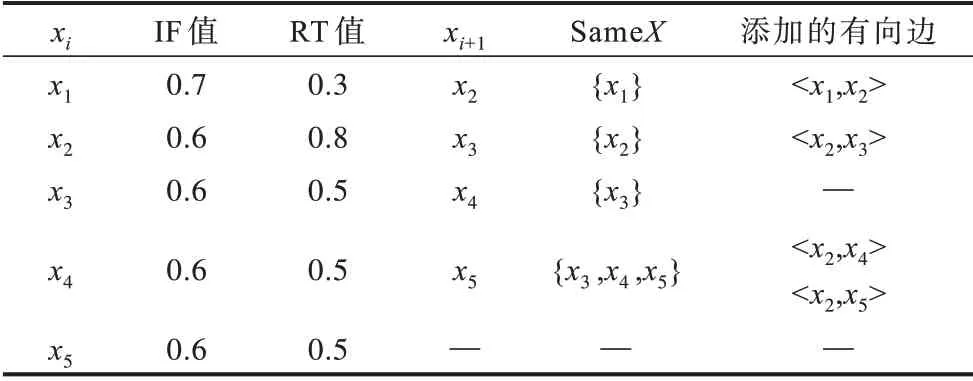
表1 算法1 元素取值示例Table 1 Example of element values of algorithm 1
3.3 数据集抽取和CPT 计算
本节基于KG 三元组抽取数据集,利用三元组中的关系和尾实体来生成KGBN 中包含n个变量取值的组合,并统计变量取值组合的个数,从而利用DAG 和数据集计算得到KGBN 的CPT。
基于KG 三元组抽取数据集的过程为:
1)从GK的三元组集合T中抽取满足以下2 个条件的三元组:
(1)三元组的头实体和构建φ的实体为同一类型。
(2)三元组的关系为φ中变量所表示的关系。
2)对于这些三元组中的每一个关系,将其作为φ中的变量xi,同时将这个关系连接的不同尾实体作为变量xi的不同取值,得到变量的取值集合,记为,其中,mi为xi的取值个数。
3)利用φ中的变量及其取值得到所有可能的取值组合{d1,d2,…,dδ},其 中,δ=表示第l种变量取值组合。
接着,统计每种取值组合的个数,过程为:
1)基于前文抽取出的满足2 个条件的三元组,将其中头实体为同一个实体的多个三元组归为一条数据。
2)利用这条数据中的关系及尾实体生成φ的变量及变量取值,每条数据可生成一个包含n个变量取值的组合,若这个组合与变量取值组合dl相同,则将这个组合作为dl的一个实例。
3)根据前文所得的变量取值组合,利用KG 统计每种变量取值组合的个数,构成数据集D={(d1,ND(d1)),(d2,ND(d2)),…,(dδ,ND(dδ))},其 中,ND(dl)表示dl的实例数。
假设KG 的片段如图2 所示,其中每个关系分别连接2 种尾实体。在图1 所示的KGBN 中,共有2 个变量,每个变量有2 个取值,计算可得数据集中共有2×2×2=8 种变量取值组合,如图2 中数据集D的片段所示。利用实体“电影1”构成的多个三元组生成变量取值组合,记为d1的1 个实例,根据KG 片段统计得到d1共有2 个实例。
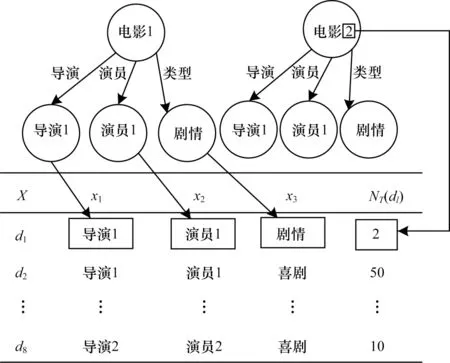
图2 数据集D 的抽取过程Fig.2 Extraction process of dataset D
在计算CPT 时,若xi无父变量,其CPT 值为xi的边缘概率分布P(xi);若xi有父变量,则其CPT 值为条件概率分布P(xi|Ppa(xi))。基于最大似然估计法[14],利用GB和数据集D计算xi的CPT 值θijk,如 式(3)所示:
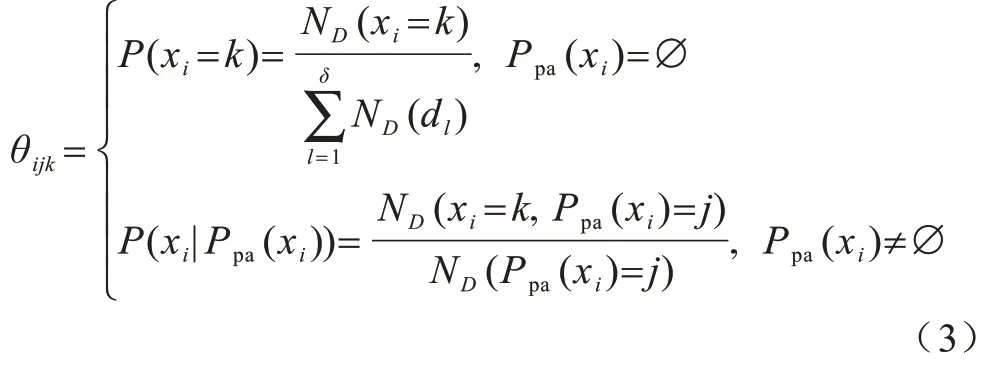
其中,ND(xi=k)为D中满足xi取值为k的实例数,为D中的实例数之和,ND(Ppa(xi)=j)为D中满足xi的父变量Ppa(xi)取值组合为第j种的实例数,ND(xi=k,Ppa(xi)=j)为D中满足xi取值为k且其父变量Ppa(xi)取值组合为第j种的实例数。
4 基于KGBN 推理的三元组构造
本节以开放世界数据中提取的包含新实体的三元组为基础,利用其中的关系及尾实体获取KGBN 推理中的证据变量及其取值,进而将新实体涉及的其他关系作为查询变量,并将推理得到的查询变量取值作为关系连接的尾实体,从而构造出新的三元组。开放世界数据中的三元组可以用经典的LSTM-CRF[21-22]技术获取。BN 精确推理的计算复杂度相对于变量个数成指数增长,变量消元(Variable Elimination,VE)方法[23]利用变量间的条件独立关系减少推理过程中的变量个数,降低计算复杂度,使得整体计算复杂度未必相对于变量个数成指数增长[18],因此,本文采用VE作为KGBN推理算法。
将从数据中提取的三元组集合记为W=,其 中,h'为从数据中提取的新实体。将集合W中的关系作为φ中的证据变量,记为证据变量集合Xz,并将关系连接的尾实体作为各证据变量的取值。将集合X中存在而Xz中不存在的变量作为查询变量,记为查询变量集合Xq,最大条件概率的阈值记为α。
基于KGBN 推理构造三元组的基本思想如下:首先,针对集合Xq中任意一个查询变量x,计算得到包含φ中所有概率分布的集合,并将Xz中各个变量的取值代入其中;其次,对除x外所有属于X但不属于Xz的变量设置消元顺序,对其中每个变量进行求和消元,得到一个新的概率分布集合;然后,将概率分布集合中的所有函数相乘得到关于x的函数,进而利用函数计算得到x各个取值的条件概率,并找到最大条件概率P(x=k|Xz);随后,判断最大条件概率是否大于等于阈值α,若是,则利用满足大条件概率的k值构造三元组(h',x,k);最后,将三元组和集合W加入GK的三元组集合T中。重复上述过程,直到循环结束。基于KGBN 推理的三元组构造过程如算法2所示。
算法2基于KGBN 推理的三元组构造


算法2 的执行代价主要取决于集合Xq中的查询变量个数和每次推理中消元的变量个数,算法2 的总执行代价为查询变量的个数和每次推理中消元执行代价之和的乘积。
在封闭世界下执行KGC 任务时,首先,将KG 中包含同一个头实体的多个三元组作为一个集合;其次,利用其中的关系及尾实体作为证据变量及证据变量的取值;然后,将集合X中其他变量作为查询变量;最后,针对查询变量进行KGBN 推理,利用算法2 得到新的三元组。
以图1 中的KGBN 为例,假设从数据中提取到三元组集合W={(“电影”,“导演”,“导 演1”),(“电影”,“演员”,“演员1”)},证据变量及其取值为{x1=“导演1”,x2=“演员1”},查询变量为x3。利用算法2计算P(x3),首先得到KGBN 中的概率分布集合{P(x1),P(x2|x1),P(x3|x2)},设置变量消元顺序为{x1,x2}。从概率分布集合中删去包含x1的函数,并生成新函数,得到{g(x2),P(x3|x2)}。类似地,消去x2,得到P(x3=“剧情”|x2=“演员1”)=0.05,P(x3=“喜剧”|x2=“演员1”)=0.95,构造三元组(“电影”,“类型”,“喜剧”)。
5 实验验证
将本文知识图谱补全方法记为BN-KGC,使用DBpedia50k、DBpedia500k[19]和FB15k[20]数据集在开放世界下测试BN-KGC 的效率和有效性。BN-KGC也可用于封闭世界KGC 任务,本文基于OpenKE 平台[24]实现TransE[8]、TransH[9]和TransR[11]方 法,在封闭世界下测试BN-KGC 的有效性。
FB15k 数据集包含14 951 个实体和1 345 个关系,DBpedia50k 和DBpedia500k 数据集分别包含49 900 个实体、654 个关系和517 475 个实体、654 个关系。3 种数据集的三元组个数划分情况如表2 所示。
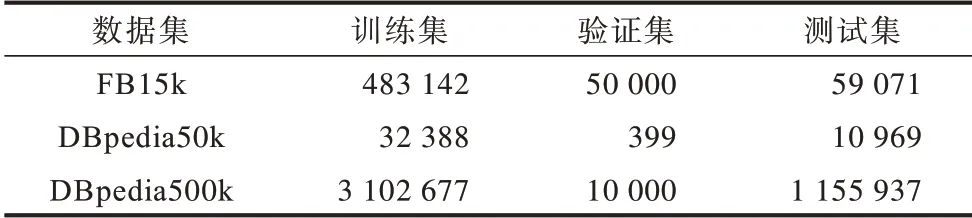
表2 3 种数据集的三元组个数统计Table 2 Statistics of the number of triples in three datasets
本文定义了最大条件概率的阈值α,利用α来决定KGBN 推理所得的取值是否能够作为构造三元组的实体。若α值过小,则会导致结果的准确率降低;若α值过大,则会导致所得结果的数量减少。本文利用验证集进行阈值设置,首先对验证集中的三元组进行KGBN 推理,得到构成这些三元组的正确结果的条件概率(正确结果的条件概率不一定为最大条件概率),进而利用这些条件概率计算平均值并作为阈值α,本文通过测试将阈值α设置为0.95。
5.1 结构构建效率测试
为了验证本文KGBN 构建方法的有效性,对KGBN 构建方法的执行时间进行测试。首先,针对KGBN 中不同的变量个数,测试在不同数据集下计算IF 值和RT 值的执行时间。计算IF 值、RT 值的执行时间结果分别如图3 和图4 所示,从中可以看出,执行时间均随变量个数的增多而增加。其中,在FB15k 数据集下执行时间最长,在DBpedia500k 数据集下执行时间次之。对从KG 中抽取数据集的执行时间进行测试,结果如图5 所示。从图5 可以看出,抽取数据集的执行时间随KGBN 中变量个数的增多而增加,其中,在DBpedia500k 数据集下执行时间最长,在FB15k 数据集下执行时间次之。
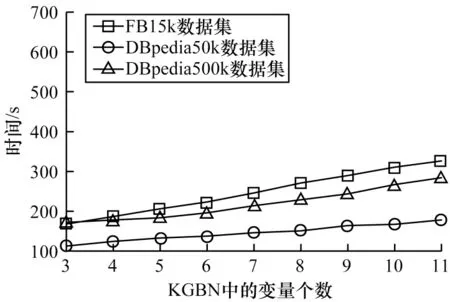
图3 计算IF 值所需的执行时间Fig.3 The execution time required to calculate the IF value

图4 计算RT 值所需的执行时间Fig.4 The execution time required to calculate the RT value
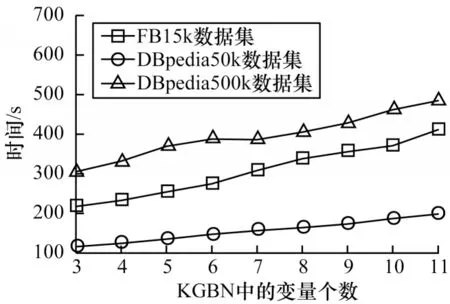
图5 抽取数据集所需的执行时间Fig.5 The execution time required to extract the dataset
将同个数据集下的IF 值、RT 值计算和数据集抽取的执行时间进行对比,在FB15k、DBpedia50k 和DBpedia500k 数据集下的执行时间情况分别如图6~图8 所示。从中可以看出,在同等条件下RT 值计算的执行时间总体大于IF 值计算的执行时间,且数据集抽取的执行时间略高于IF 值计算的执行时间,但远低于RT 值计算的执行时间。

图6 FB15k 数据集下的执行时间比较Fig.6 Comparison of execution time in FB15k dataset

图7 DBpedia50k 数据集下的执行时间比较Fig.7 Comparison of execution time in DBpedia50k dataset
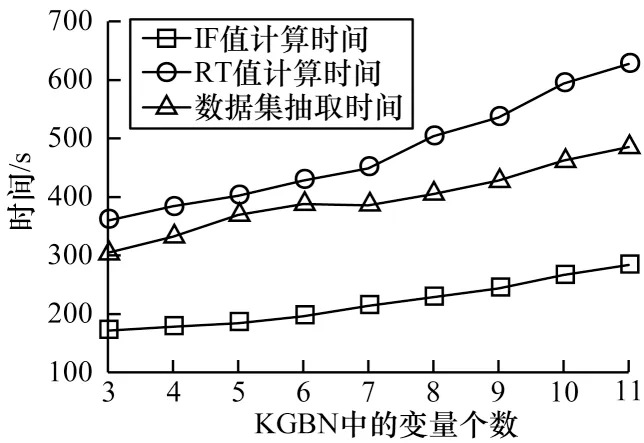
图8 DBpedia500k 数据集下的执行时间比较Fig.8 Comparison of execution time in DBpedia500k dataset
测试含不同变量个数时KGBN 结构构建的执行时间,结果如图9 所示。从图9 可以看出,构建KGBN 的执行时间随变量个数的增多而增加,在DBpedia500k 数据集下的执行时间最长,在FB15k 数据集下的执行时间次之。这表明在KGBN 构建的执行时间中IF 值和RT 值计算的执行时间占比很小,同时测试中针对3 个~11 个IF 值的降序排列以及针对3 个~11 个变量的DAG 构建花费的时间远小于IF 值计算的时间,这说明本文KGBN 构建方法的执行时间主要取决于CPT 的计算时间。
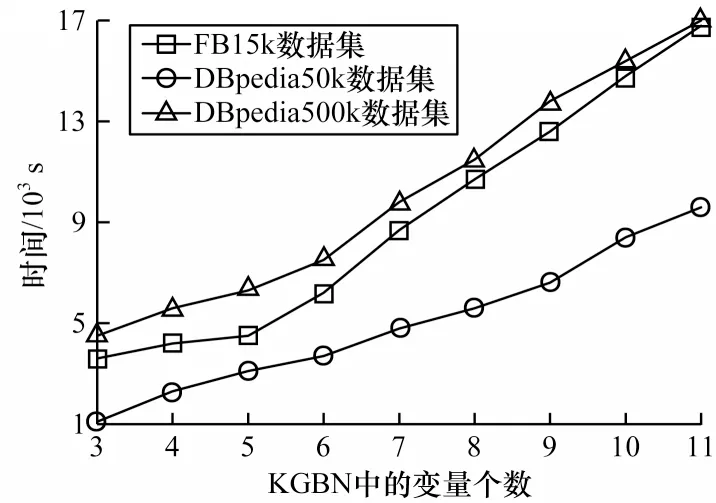
图9 KGBN 构建所需的执行时间Fig.9 Execution time for KGBN build
5.2 开放世界KGC 方法有效性测试
5.2.1 三元组类型预测
在三元组类型预测任务中,测试集中的三元组被称为正确三元组,将测试集中的三元组随机替换实体,得到错误三元组。其中,正确三元组被预测为正记作TP,错误三元组被预测为正记作FP,正确三元组被预测为负记作FN。三元组类型预测的评估指标分别为准确率(Precision)、召回率(Recall)及F1 值。
首先,利用训练集和验证集分别构建包含5 个、8 个和11 个变量的KGBN,并将阈值α设置为0.95;然后,利用测试集中的三元组进行KGBN 推理,得到三元组中关系连接尾实体的条件概率,将条件概率不小于阈值的三元组记为正,否则记为负,进而得到三元组类型预测结果。
当KGBN 中包含5 个变量时,三元组类型预测结果的各项指标如图10 所示。从图10 可以看出,随着查询变量个数的增多,预测结果的准确率略有下降,而召回率呈上升趋势,在FB15k 数据集下预测结果的F1 值保持相对稳定的趋势,在DBpedia 数据集下预测结果的F1 值呈先上升后下降的趋势。当KGBN 中包含8 个变量时,三元组类型预测的结果如图11 所示。从图11可以看出,预测结果的准确率、召回率和F1 值均有明显的提升。其中,在FB15k 数据集下预测结果的准确率和F1 值较好,在DBpedia 数据集下预测结果的召回率较好。当KGBN 中包含11 个变量时,三元组类型预测的结果如图12 所示。从图12 可以看出,预测结果的准确率随着查询变量个数的增多而略有下降,但召回率和F1 值随着查询变量个数的增多而明显提升。

图10 KGBN 变量个数为5 时的三元组类型预测结果Fig.10 Prediction results of triple type when the number of KGBN variables is 5

图11 KGBN 变量个数为8 时的三元组类型预测结果Fig.11 Prediction results of triple type when the number of KGBN variables is 8

图12 KGBN 变量个数为11 时的三元组类型预测结果Fig.12 Prediction results of triple type when the number of KGBN variables is 11
在实际中,准确率和召回率难以同时兼顾,一个较高时另一个总会较低,因此测试中通常采用F1 值来综合度量方法的有效性。结合图10~图12 的结果可以看出,随着查询变量个数的增多,针对同一个头实体构造的三元组个数增加,因此,预测结果的召回率有所提升。虽然证据变量的减少可能会导致预测结果的准确率下降,但是预测结果的F1 值会有一定提升或能保持相对稳定的趋势。
5.2.2 链路预测
本文分别在3 个数据集上执行链路预测任务,进一步测试BN-KGC 实现开放世界KGC 的有效性。链路预测能够预测三元组缺失的头实体或尾实体,可用于KGC 任务。将测试集中的三元组称为正确三元组,对于任意一个正确三元组,本文利用实体集中所有实体替换其尾实体构造参考集,打分排序后根据正确三元组在参考集中的排名计算MR 和Hits@10 指标。MR 用于度量正确三元组排名的平均值,Hits@10 用于衡量排名在前10 的正确三元组个数占三元组总个数的比例。利用前文构建得到的KGBN,将基于KGBN 推理得到三元组中关系连接尾实体的条件概率作为评分函数,进而计算BN-KGC的MR 和Hits@10。链路预测结果如表3 所示,从表3 可以看出,在FB15k 数据集下,当KGBN 中变量和查询变量个数分别为8 和3 时预测的MR 结果最小,当KGBN 中变量和查询变量个数分别为8 和5 时预测的Hits@10 结果最大。在DBpedia50k 数据集下,当KGBN 中变量和查询变量个数分别为8 和5 时取得的MR 和Hits@10 均为最好。在DBpedia500k数据集下,当KGBN 中变量和查询变量个数分别为11 和6 时预测 的MR 结果最小,当KGBN 中变量和查询变量个数分别为11 和4 时预测的Hits@10 结果最大。从总体来看,当KGBN 中变量和查询变量个数分别为8 和5 时预测结果最好,因此,本文采用该组结果与现有的开放世界KGC 方法进行比较。
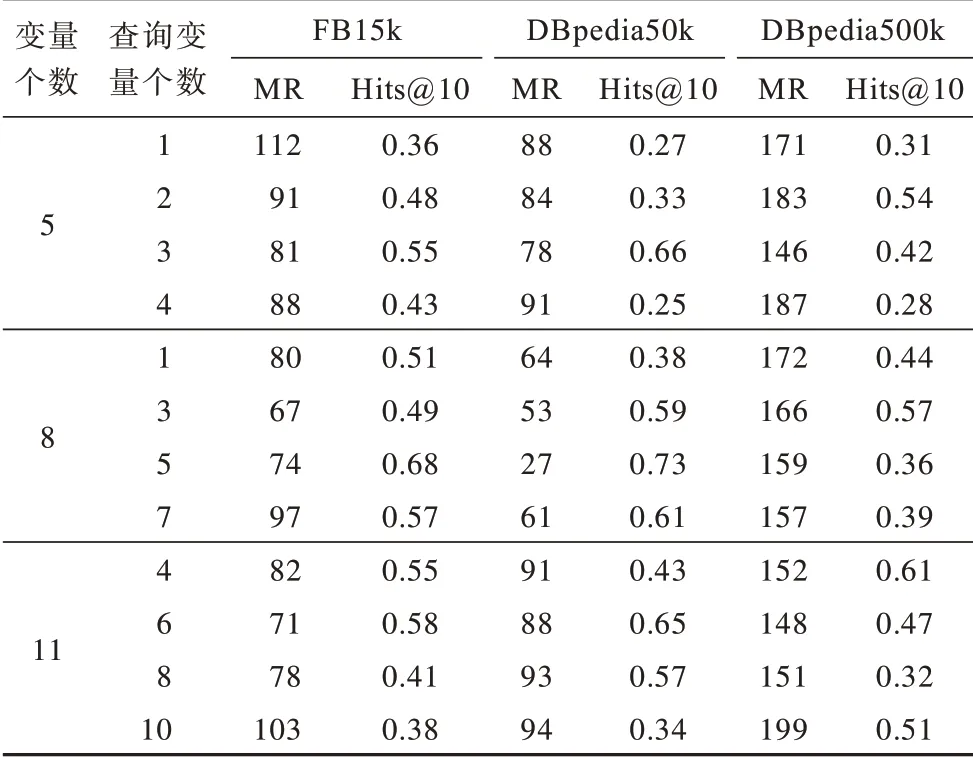
表3 开放世界下的链路预测结果Table 3 Link prediction results in open-world
如表4 所示,在DBpedia 数据集下将ConMask[12]方法与BN-KGC 方法执行的链路预测结果进行比较。在DBpedia50k 数据集中,ConMask 的MR 和Hits@10 最佳,这是由于KGBN 的预测效果受初始KG 影响,当初始KG 规模较小时难以全面地获取关系之间的相关性,从而导致BN-KGC 的预测效果略差于ConMask。在DBpedia500k 数据集下将BN-KGC 方法和ConMask 方法的链路预测结果进行比较,此时BN-KGC 方法预测结果的MR 优于ConMask 方法。实验结果表明,当初始KG 规模较大时BN-KGC 方法可以较全面地获取关系之间的相关性,从而有效完成开放世界KGC 任务。
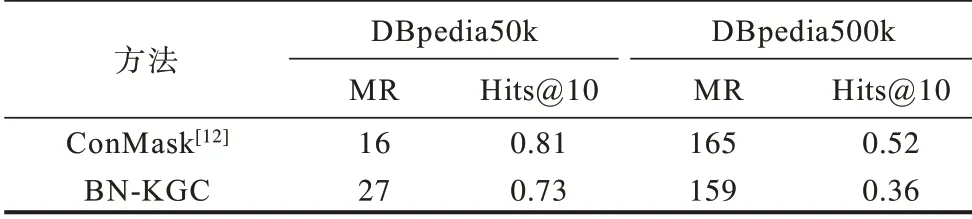
表4 开放世界下的链路预测结果比较Table 4 Comparison of link prediction results in open-world
5.3 封闭世界KGC 方法有效性测试
BN-KGC 方法也可用于封闭世界KGC 任务,为了测试基于BN-KGC 方法实现封闭世界KGC 的有效性,分别在3 个数据集下基于OpenKE 平台得到TransE、TransH 及TransR 的三元组类型预测结果和链路预测结果,并将其与BN-KGC 进行比较。
封闭世界下的链路预测结果如表5 所示,从表5可以看出,在FB15k 数据集下,基于BN-KGC 方法预测的MR 结果达到77,仅排在TransR 之后。在DBpeida50k 数据集下,基于BN-KGC 方法预测的MR结果最佳。在DBpedia500k 数据集下,基于BN-KGC方法预测的MR 结果和Hits@10 均为最佳。三元组类型预测结果的准确率、召回率和F1 值如图13 所示。从图13 可以看出,在FB15k 和DBpedia500k 数据集下,基于BN-KGC 方法预测结果的准确率和F1 值最佳,在DBpedia50k 数据集下,基于BN-KGC 方法预测结果的准确率、召回率和F1 值均为最佳。实验结果表明,本文方法同样适用于封闭世界KGC 任务,即BN-KGC 方法具有有效性。
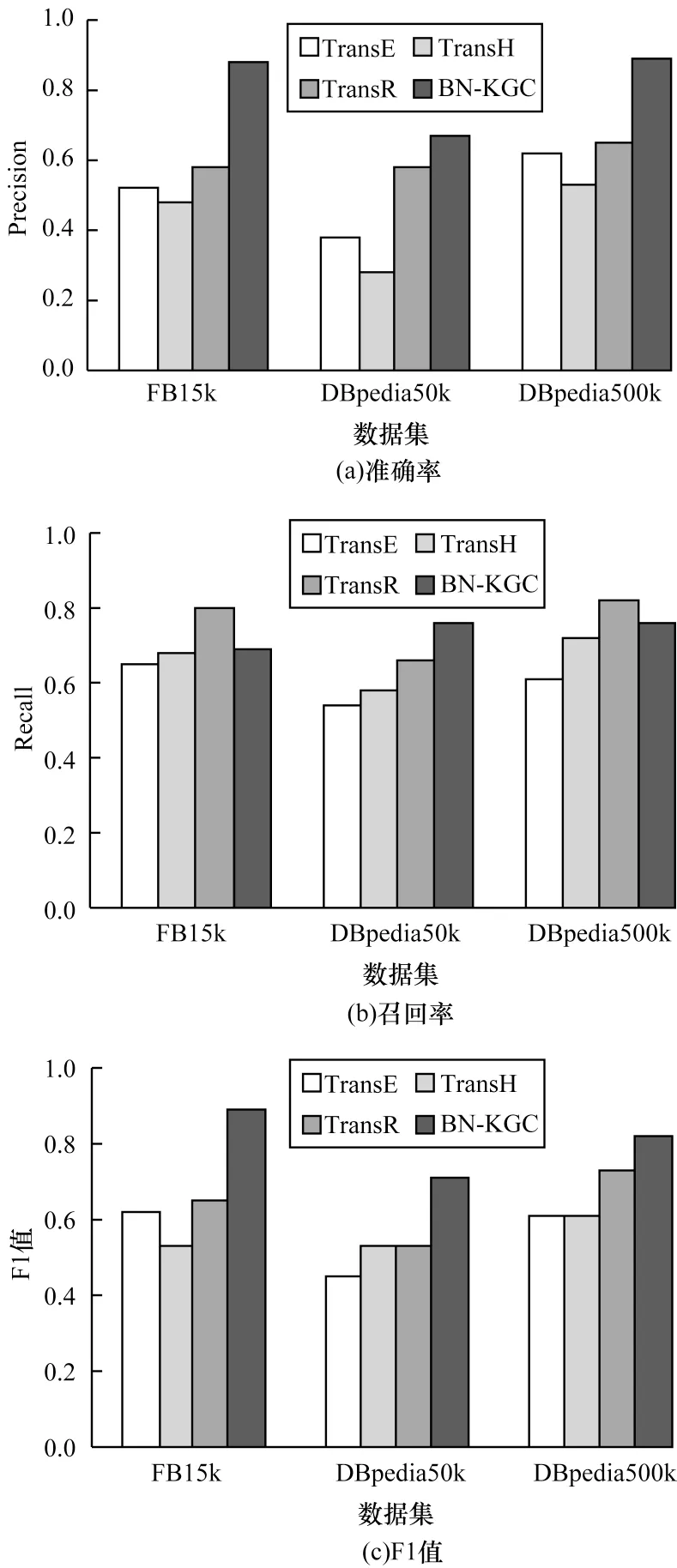
图13 封闭世界下的三元组类型预测结果比较Fig.13 Comparison of prediction results of triple type in closed-world

表5 封闭世界下的链路预测结果比较Table 5 Comparison of link prediction results in closed-world
本节基于FB15k 和DBpedia 数据集,首先,测试KGBN 构建方法的时间效率,实验结果表明,KGBN的结构构建执行时间主要取决于变量个数,且其中用于计算CPT 的执行时间最多;其次,在开放世界下进行三元组类型预测实验,对比不同变量个数、不同查询变量个数下的KGBN 预测结果,结果表明,本文方法能够有效提升预测结果的召回率,并且在最好情况下预测结果的准确率高达0.88;然后,在开放世界下进行链路预测实验,并将本文方法的实验结果与现有的开放世界方法进行比较,结果表明,当初始KG 达到一定规模时,基于本文方法预测的结果在MR 指标上有所提升,达到159;最后,在封闭世界下分别进行三元组类型预测和链路预测任务,结果表明,基于本文方法预测三元组类型时的准确率和F1 值明显高于基于表示学习的其他方法,并且在DBpedia500k 数据集下进行链路预测时,本文方法的MR 和Hits@10 分 别达到107 和0.66。
6 结束语
本文使用BN 描述KG 中同类实体涉及的关系之间的依赖性,提出KGBN 模型构建方法和基于KGBN 推理的三元组构造方法。实验结果表明,该三元组构造方法针对新实体能够同时构造多个三元组,有效提升KGC 任务中新知识的全面性。随着KG 中知识的增加以及变化,关系间的依赖性也会发生相应变化,导致KGBN 推理的准确率降低。因此,如何将KG 中的新知识用于KGBN 构建,实时反映关系间的依赖性,进而提升KGC 方法的时效性,将是下一步的研究方向。
