基于价电子理论的Ag-Sn金属间化合物形成机理
2021-06-15马立民齐楚晗王乙舒
马立民,齐楚晗,王乙舒
(1.北京工业大学材料科学与工程学院,北京 100124; 2.北京工业大学新型功能材料教育部重点实验室,北京 100124)
自2006年《关于限制在电子电器设备中使用某些有害成分的指令》标准在全球推行实施以来,互连焊点的材料逐步向无铅钎料转变. 无铅钎料的主要成分为Sn基合金,其中以SnAgCu系钎料应用最广[1]. 为了使无铅钎料的性能达到SnPb钎料的优良稳定性,诸如Cu、Ag、Ni等贵稀金属在Sn基钎料中所占比例逐步提高,虽然提高了Sn基无铅钎料的稳定性,但脆性金属间化合物(intermetallic compounds, IMCs)的数量也随着加入的贵稀金属的种类和数量越来越多[2]. 近10年,三维封装密集程度的不断提高使得SnAgCu系钎料与焊盘所产生的金属间化合物的占焊点体积比例越来越大,Lee等[3]认为,焊点尺寸的减小使焊点成为最薄弱的连接环节. 相应地,焊点的机械性能、导电性能和热稳定性等都将成为影响互连微焊点可靠性的关键因素. 因此,对IMCs的相关性质展开系统性研究,并从机理上对焊点内部IMCs的相变反应和微观组织的演变有较为深入的认识与理解显得极其重要.
Ag3Sn作为Cu/SnAgCu/Cu焊点中唯一生成的Ag-Sn IMCs一般在焊点内部形成,不同于Cu-Sn系金属间化合物通常位于钎料与基板界面处,虽然数量较少,但在电迁移条件下会继续长大,对于焊点内部基体的力学和电学性能造成较大影响[4]. 当SnAgCu钎料中Ag的质量分数较低时,焊接后快速冷却,纳米颗粒状的Ag3Sn相弥散分布在基体中起到强化基体的作用,但也会在Cu6Sn5晶粒上形成并影响其生长[5]. 在钎料中w(Ag)≥3.5%时,焊接后的冷却过程中在基体内会生成尺寸较大的板片状或者块状Ag3Sn,同时在后续的服役条件下也会出现粗大的板条状Ag3Sn,降低焊点的抗冲击及抗跌落性能[6]. 实验表明[7],片状的Ag3Sn弥散分布在Cu/SnAg/Cu焊点的β-Sn相中,由于弥散强化机制的原因,Cu/SnAg/Cu焊点具有较好的力学性能. 但当w(Ag)=4.0%时,焊点内部将形成板状的Ag3Sn相,该脆性相的形成会明显恶化焊点的性能.
相比于Cu-Sn界面反应而言,现有的关于Ag-Sn扩散反应的研究相对较少,对于Ag3Sn的形成机理研究更是不系统,且对于Ag-Sn界面反应中的主要扩散元素均有不同声音出现,Chen[8]在研究Ag-Sn-Cu三元合金的相平衡时发现Sn元素在Cu/SnAg/Cu焊点界面反应中是最活跃、扩散最快的元素;在研究SnAg/Au凸点的界面反应时,发现在Sn-Ag界面反应中Ag是不易移动的,这些都从侧面印证了Ag-Sn界面反应中是Sn向Ag中扩散. 而Brunson等[9]在研究中发现,Ag在Sn中的扩散速度比Sn自身的扩散速度要快一些,并且扩散速度随温度升高而加快. Sen等[10]采用Ag-Sn薄膜来研究其界面扩散反应,发现了2种不同的扩散行为:Sn通过晶界扩散进入Ag和Ag通过体扩散进入Sn. Marinkovic等[11]在室温下测得Ag和Sn界面反应得到Ag3Sn的互扩散系数为6.6×10-13cm2/s.
本文采用固体与分子经验电子理论(empirical electron theory, EET),通过计算Ag-Sn固溶体模型结合能确定主要扩散元素,在确定扩散元素的基础上,利用计算得到的Ag、Sn、Ag3Sn的价电子结构阐述Ag3Sn形成机理.
1 IMCs理论计算研究现状
在IMCs的理论研究方面,主要应用第一性原理(first principle calculation)研究Sn-Cu或Sn-Ni化合物的晶体结构、稳定性[12]. 分子动力学(molecular dynamics, MD)则主要应用于体系中扩散和IMCs生长机理方面的问题研究. 对于Ag-Sn化合物的研究以实验较多,理论研究方面的报道较为少见. 也有研究认为,Cu、Ag、Au等贵金属同属元素周期表的ⅠB副族,所以对Sn-Cu化合物扩散机理进行过研究后,他们认为Ag和Cu的扩散趋势具有相似之处,不需要再另外研究[13].
1.1 第一性原理
密度泛函计算和平面波赝势方法常用来研究无铅焊点的稳定性和力学性能[12]. 王宏伟等[14]基于上述方法研究了Ni3Sn4和Cu6Sn5的结构稳定性和弹性性能,得到了Ni3Sn4和Cu6Sn5的剪切模量、弹性模量和泊松比等参量,并比较了它们的物理和力学性能. Ghosh等[15]系统地计算研究了Cu6Sn5的2种相η和η′的晶体结构和稳定性,所获得的理论晶格常数与实验测量值吻合较好. Chen等[16]则计算了Cu6Sn5和Cu3Sn两种IMCs的弹性性能. 王娟等[17]研究了Ni-Sn IMCs中的Ni3Sn、Ni3Sn2等二元化合物的电子结构和力学稳定性. Yu等[18]研究了η′-(Cu,Ni)6Sn5晶体结构的稳定性,并认为这种Ni占位结构比η′-Cu6Sn5更稳定.
1.2 分子动力学
Tu等[19]在研究固态的Cu/Sn界面反应时发现长程有序的η′-Cu6Sn5相的形成,室温下Cu在η′相中为晶界扩散,进入Sn中则为间隙扩散. 生长动力学显示η′相呈线性生长. 由于Cu熔点较高,从Cu晶格中释放原子较难,导致室温下扩散速度受限. Tu[20]还提出,Cu3Sn的形成是以消耗Cu6Sn5为代价,即在Cu/Cu6Sn5界面形成而非Cu/Sn界面,动力学曲线呈抛物线. 而Bhedwar等[21]的发现与上述研究事实相反,在200 ℃下形成η- Cu6Sn5时Sn为主要扩散元素且η-Cu6Sn5的动力学曲线为抛物线而非线性,因为高温下体扩散占主导,而低温时短程扩散为主要扩散机制. Onishi等[22]的研究证实了Bhedwar的结论,同时在190~220 ℃温度区间内分别计算了Cu6Sn5和Cu3Sn的互扩散系数
(1)
(2)
通过比较可以看出,Cu3Sn的互扩散活化能更高,也说明Cu3Sn的生长相比于Cu6Sn5需要更高的温度.

2 计算方法
1978年,余瑞璜等[25]在L.Pauling原子状态杂化理论[26]的基础上提出了固体或分子中原子价层电子分布的一种描述方法,即EET理论. 以构造原子双态杂化为基础,通过解L.Pauling键距方程确定晶体原子各条共价键上电子分布及原子所处状态. 相比于第一性原理应用的泛函密度理论[27],EET理论以能带理论、价键理论及电子浓度理论为出发点,因此不需要计算烦琐的薛定谔方程,相对来说更简洁易懂;且只需获得晶体的一些初始数据就可以计算第一性原理无法应用的原子数量较多的大体系;除此之外,EET理论虽然计算晶体的微观性质,却能很容易地和晶体的宏观性质及实验结果产生联系,进而为一些实验结果提供有力的解释[28].
应用EET理论,确定晶体内各组元原子的状态并描述晶体的价电子结构,建立经验方程求得晶体中总价电子、晶格电子、共价电子数目和单键半距,利用键距差法(bond length difference, BLD)求得晶格中各原子之间共价电子的分布[29],建立其晶体或分子的价电子结构,从原子角度分析解释Ag-Sn界面反应的相变过程.
通过BLD法得到的晶格常数的统计值,能满足一般情况下的计算. 为进一步提高EET理论的计算精度,Lin等[29]在EET中BLD法的基础上提出了自洽键距差(self-consistent bond length difference,SCBLD)法,引入了“迭代自洽方法”. 通过SCBLD法,可以获得精度较高的晶格常数理论计算值及优化的β值. SCBLD法的计算过程如图1[30]所示.

图1 SCBLD法的计算过程[29]Fig.1 Calculation process of self-consistent bond length difference method[29]
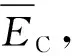
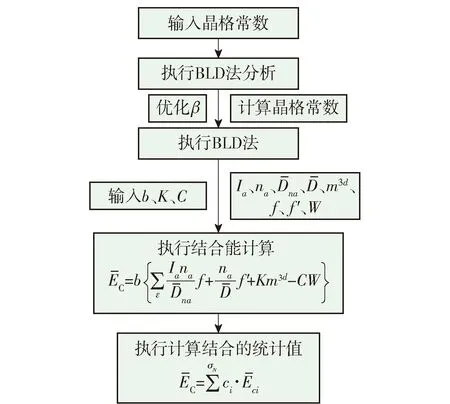
图2 结合能计算过程[31]Fig.2 Calculation process of cohesive energy[31]
3 Ag-Sn系统主扩散元素
IMCs是焊盘与钎料在焊接中通过发生化学反应,产生良好冶金结合的证明[13]. 由于IMCs的宏观、微观特征性质与焊盘和钎料的不尽相同对焊点可靠性产生了关键影响,因此了解互连结构中IMCs相的形成及转变成为当务之急.
虽然Ag在SnAgCu钎料中的质量分数很低,但在反应温度下,钎料中的Ag会快速与熔融的Sn发生反应. 在图3的Ag-Sn二元相图上[33],仅存在2种金属间化合物. 一种是无序结构的Ag4Sn(ζ相),有报道称在450 ℃下将SnAg焊点退火720 h后发现了少量的Ag4Sn[34];另一种是属正交晶系的短程有序的Ag3Sn相,为Cu/SnAgCu/Cu焊点中常见IMCs之一.
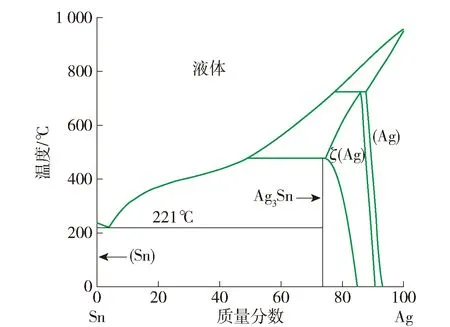
图3 Ag-Sn二元相图[32]Fig.3 Phase diagram of Ag-Sn[32]
3.1 Ag和Sn的价电子结构
Ag的结构单元为面心立方晶胞,在Ag结构单元中,有2种共价键,它们各自的实验键距和等同键数分别为
Ag结构单元中2种共价键的键距分别为
DnA=2R(1)Ag-βlgnA
(3)
DnB=2R(1)Ag-βlgnB
(4)
式中β=0.057 8 nm.
用式(4)减去式(3),再做适当变形,得
(5)
根据
(6)
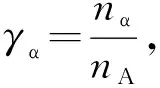
(7)
所以,Ag结构单元中任一共价键的共价电子数nα=nAγα. Ag结构单元中2种共价键的理论键距分别为
(8)
(9)
(10)
Ag的价电子结构可按照上述过程求出,详细的价电子结构参数如表1所示.
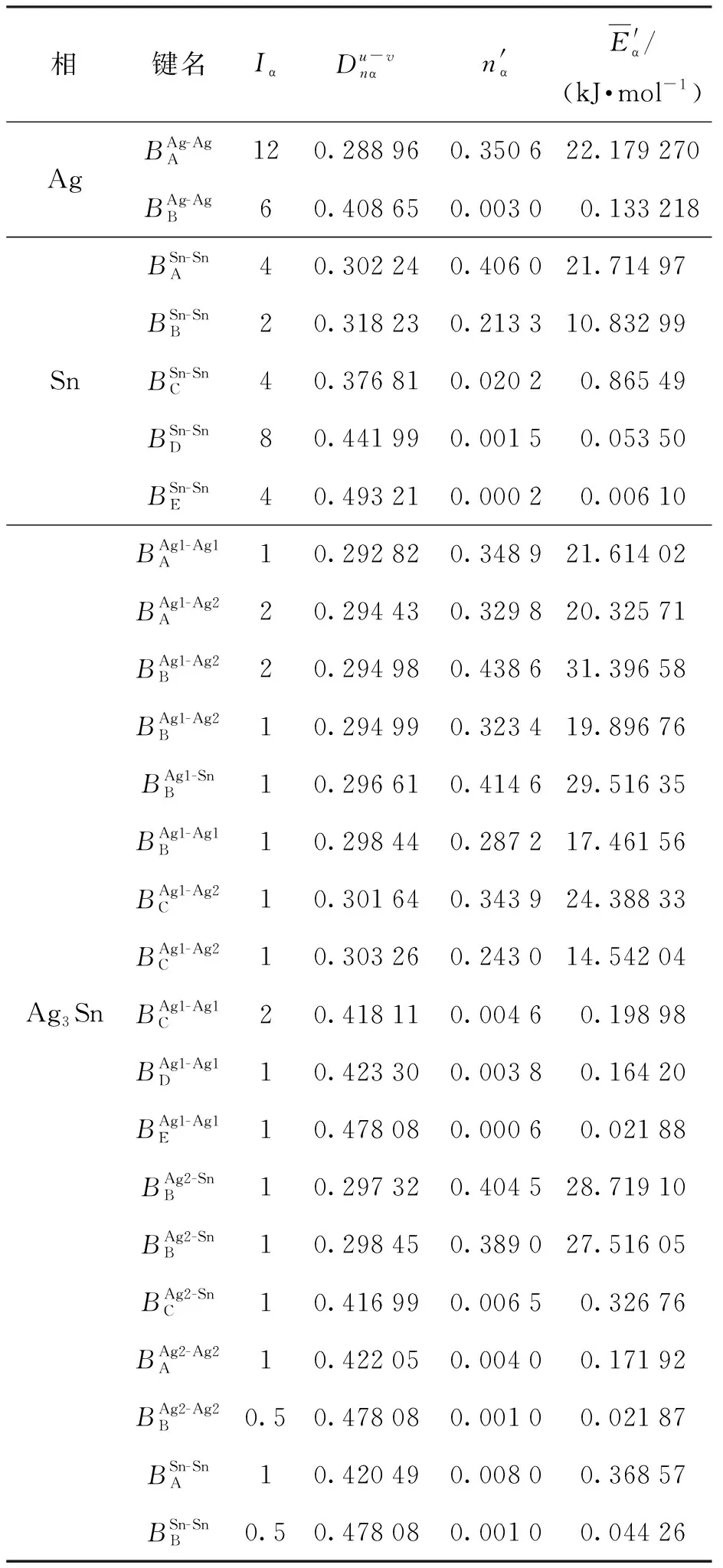
表1 Ag、Sn和Ag3Sn价电子结构参数
Sn的结构单元为四方晶胞,如图4(a)所示. 在Sn结构单元中,有5种共价键,它们各自的实验键距和等同键数分别为
Sn的价电子结构可按照上述求解Ag的过程求出,这里式(3)(4)中的β=0.057 2 nm.
3.2 Ag-Sn固溶体模型建立
在Ag-Sn界面反应中不论是Ag扩散进入Sn还是Sn扩散进入Ag都会形成固溶体,因此这里以Ag-xSn和Sn-xAg两种结构单元代表可能形成的2种固溶体,x表示扩散元素进入单个晶胞的原子个数占比. 下面以Sn-xAg结构单元为例,Ag-xSn结构单元的计算方法相同,可参照下述方法.
当Ag原子溶入Sn晶胞中后将占据Sn原子的位置. Ag加入Sn晶胞后所有的点阵位置都是由一种X原子占据,X原子既不是Ag原子,也不是Sn原子,而是一种假设的Sn+xAg原子混合成的原子,如图4(b)所示. 其单键半距、共价电子数、成键能力、屏蔽系数等性质为组成固溶体的各种元素原子的加权平均值[35]. 假设有1个Ag原子进入Sn晶胞,此时x取值为0.25,得出
(11)
(12)
(13)
(14)

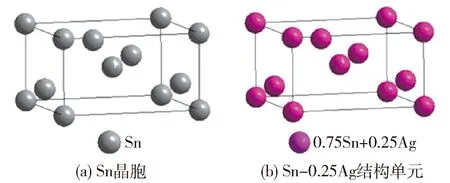
图4 Sn和固溶体晶胞模型Fig.4 Sn unit cell and solid solution models
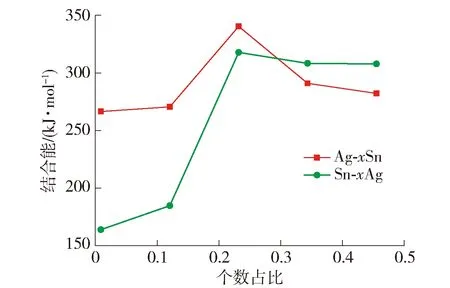
图5 Ag-Sn固溶体模型结合能曲线Fig.5 Cohesive energy curves of Ag-Sn solid solution models
同理,按照上述步骤可以求出Ag-xSn结构单元的价电子结构参数和结合能,假设有1个Sn原子进入Ag晶胞,此时x取值为0.25,Ag3Sn的形成机理如图6所示,其中图6(a)为Ag-0.25Sn结构单元示意图.
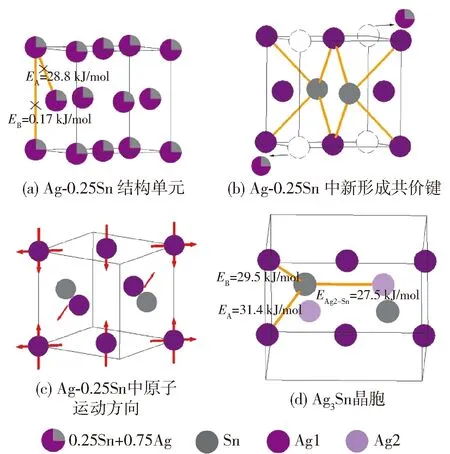
图6 Ag3Sn形成机理模型Fig.6 Formation mechanism model of Ag3Sn
Sn的熔点为232 ℃,在回流焊接温度下,Sn会变成熔融状态,而Ag的熔点接近1 000 ℃,在250 ℃的温度下是不会熔化的,处于固态的Ag对于晶格内Ag原子的束缚能力要比处于熔融状态下的Sn对晶格内原子的束缚能力强很多,这样就形成了熔融状态的Sn包裹着微米级的Ag颗粒的状态,在这种状态下会形成Ag3Sn[36].
从图5的结合能曲线可以看出,当x的取值在[0,0.25],Ag-xSn结构单元和Sn-xAg结构单元的结合能均处于上升阶段,虽然Sn-xAg结构单元的上升速率不及Ag-xSn结构单元. 在EET理论中结合能是指1 mol物质从自由原子形成固态物质时所释放的能量或是从固态物质分解为自由原子时所吸收的能量[37]. 根据结合能的定义,结合能越大,物质在结合或分解时释放或吸收的能量也就越多,形成或破坏的物质也就越不易被分解或还原,因此这一阶段2种结构单元均处于进入晶胞原子越多,结合能越大,结构越稳定的状态. 且Ag-0.25Sn结构单元的结合能为最大值,这说明Ag-0.25Sn在这一系列结构单元中稳定性最好,且结构单元内的原子比例与Ag3Sn晶胞内的原子比例相同,最有可能继续转变为化合物Ag3Sn.
当x的取值在[0.25,0.5]时,2种结构单元的结合能开始迅速下降,说明随着进入单个晶胞的原子数增多固溶体结构单元愈发不稳定,不能稳定存在就不具备转变为化合物的先决条件. 因此可以判断在Cu/SnAgCu/Cu焊点中Ag3Sn是唯一形成并稳定存在的Ag-Sn IMCs. 综上所述,Ag-Sn界面反应中Sn为主要扩散元素,并形成化合物Ag3Sn.
4 Ag3Sn的形成过程
4.1 Ag3Sn的价电子结构
Ag3Sn的晶体结构为正交晶系,空间群为Pmmn(59),如图6(d)所示,晶胞中有6个Ag原子和2个Sn原子. 该晶体中共有18种共价键,下面仅列出几种实验间距和等同键数的计算结果,其余共价键采用Diamond软件测量出实验间距并计算等同键数,计算方法可参照3.1小节的详细步骤,最终得到的结果在表1中展示.
4.2 Ag3Sn的形成机理
Sn原子扩散进入Ag晶胞首先会形成Ag-xSn固溶体结构单元. 当固溶体结构单元变为Ag-0.25Sn时已满足Ag3Sn的成分比例,即Ag和Sn原子比为3∶1,如图6(a)所示. 此时Ag-0.25Sn结构单元的晶胞仍旧保持面心立方晶格,但在温度和时间的双重驱动下,这种无序状态的固溶体需要对结构单元内的原子进行有序化以维持稳定存在. 由于面心立方晶格的键能空间分布十分均匀,具有高度对称性,为了能够使结构单元内的原子重新排布,结构单元内仅存在的2种共价键会全部断裂,共价键的结合能分别为28.82和0.17 kJ/mol,以图6 (a)中标有黑色叉子的键为例. 此时,原子重新排布,键能也重新分布,由于原子性质的不同,扩散进入的Sn原子会与Ag原子形成结合能更强、排布更均匀的共价键,即图6(b)中的黄色键. 而结合力弱的键会使得原子间相互作用减弱,进而相互远离甚至离开结构单元. 因此形成了新的原子排布,如图6(b)所示. 新共价键的形成使结构单元晶格膨胀,原位于(110)晶面和面心位置的Ag原子也随之向外扩张,原子运动方向如图6(c)的红色箭头所示,晶胞内原有原子位置的变化导致Ag1原子变为Ag2原子,形成了同样具有高度对称性的Ag3Sn晶胞,此时Ag1和 Ag2原子与Sn原子形成的最强共价键的结合能分别为31.4、29.5、27.5 kJ/mol,如图6(d)所示.
5 结论
1) 构建Ag-xSn和Sn-xAg两种固溶体结构单元并计算了它们的结合能,确定了Ag-Sn界面反应中的主要扩散元素为Sn,印证了Chen在相关研究中得到的实验结果.
2) 在确定了Ag-Sn系统中主要扩散元素的基础上,采用SCBLD法计算得到了Ag、Sn、Ag3Sn的价电子参数和结合能.
3) 利用固溶体模型解释了Ag3Sn相变的机制. Sn扩散进入Ag晶胞先形成Ag-0.25Sn结构单元,这种无序固溶体需要有序化以稳定结构单元. Sn原子会与Ag原子形成结合能更强,排布更均匀的共价键,同时结合力弱的键会使得原子间相互作用变弱,使原子从结构单元中游离. 新共价键的形成使结构单元晶格膨胀,位于(110)晶面和面心位置的Ag原子也随之向外扩张,形成了同样具有良好对称性的Ag3Sn.
