巧用思维导图 提升数学素养

陈会文

【摘 要】思维导图具有直观性与形象性，在小学数学教学中运用思维导图引导学生归纳与总结数学知识，理清数学知识的逻辑关系，对学生建构数学知识体系，提高数学素养具有十分重要的作用。在数学教学中，教师要根据学生的特点与具体教学内容，巧用思维导图，促进学生对知识的理解，帮助学生整合知识结构，突破教学难点，促进学生发散思维的形成。教师在教学中要应用思维导图，使学生的思维具体形象地呈现，让学生分析知识之间的逻辑关系，形成数学逻辑思维，掌握数学思想与方法，突破学习障碍，实现全面发展。

【关键词】小学数学;思维导图;数学素养;提升策略

【中图分类号】G623.5  【文献标识码】A  【文章编号】1671-8437（2021）10-0196-02

思维导图体现了人的思维轨迹，可以帮助学生开拓思路，建构数学知识网络，解决学习中存在的多种问题。思维导图可以使思维可视化，使学生更好地通过探究提高解决问题的能力[1]。传统教学模式下，学生成为教师进行知识灌输的容器，缺乏学习的主观能动性，难以对知识整体把握，知识处于零散、彼此割裂的状态。而运用思维导图可以明确知识的逻辑关系，引导学生富有针对性的思考与探究，促进学生数学素养的提高。

1   巧用思维导图，促进知识的内化

教师如果照本宣科地教学，会导致学生机械性听讲与训练，难以深入理解知识，不会对知识进行概括，难以建立清晰的知识脉络。遇到数学问题时，一些学生也往往理不清思路，很难找到解决问题的最佳途径。学生处于盲目学习状态，找不到学习的方向，多数时候处于漫无目的状态，知识得不到巩固与内化，数学思维能力很难得到培养[2]。思维导图可以引导学生明确探究的方向，促进学生将知识内化。

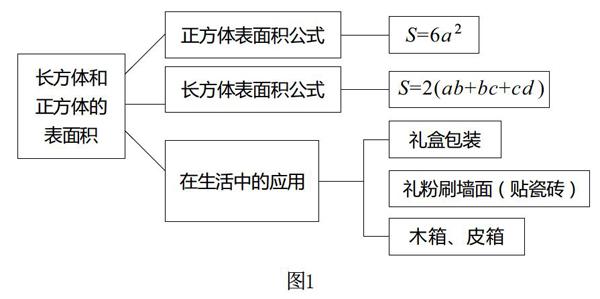
如在学习“正方体与长方体的表面积”相关知识点后，为让学生认清知识之间的规律性联系，全面而深入地把握知识内容，笔者让学生理清了正方体与长方体的表面积的相关知识，并结合这些知识在现实生活中的应用制作了思维导图，如图1所示。

这样的思维导图反映了学生对知识及其相关联系的理解，能够有效锻炼学生的逻辑思维能力。

2   巧用思维导图，整合知识

在数学学习中，学生在每个学习阶段学习的知识不同，部分学生会认为，这些知识似乎是彼此独立的，缺乏联系。这些学生在综合归纳与提炼逻辑关系的能力不强的情况下，很难整体把握数学知识体系。对此，教师可以数学思想方法为主线，引导学生绘制思维导图。教师要统观教材全局，以数学思想方法为联系点，引导学生构建知识体系，让学生通过转变角度认识到数学知识间的联系是非常紧密的。尤其是在复习课中，教师可以让学生找到知识之间的联系及共同点，帮助学生整合数学知识，提高学生概括与归纳数学知识的能力[3]。

如小学数学中“圆”的相关知识是教学重点，有关圆的知识点较多也较复杂。在学习完本节后，教师可以让学生将自己所学的知识整合，绘制成一个思维导图，把本节知识联系起来，形成逻辑关系，进而深入记忆与理解。

学生在绘制思维导图的过程中，常常会出现这样那样的问题，如对知识点间的联系缺乏深刻认识，找不到相应的联系点。这时教师要引导学生发挥想象，将知识的“断点”与相应的联系点连接起来，有效锻炼学生的逻辑思维能力[4]。同时，教师要发挥学生互动合作的作用，通过思维导图的共享，使学生了解同伴的思维过程，这样既有助于让学生对自己绘制的思维导图进行完善与优化，也有助于加强学生间的交流，开拓学生的数学思维。

3   巧用思维导图，强化知识间的联系

即便对数学知识有一定的理解与掌握，学生在运用中还是会出错误。这主要是因为学生做题时不能很好审题，未能理解题干的意思，以致不能调动自身的知识储备，不能找到解决问题的思路，难以更有效地解决问题。对此，教师要帮助学生理解问题，正确分析题意，理清解决问题的思路，使学生能够正确解决问题。思维导图在帮助学生理清知识之间的联系方面可以发挥有效作用。运用思维导图，教师可以清晰呈现数学问题的数量关系，找出问题解决的关键点及影响学生打开思路的因素[5]。学生根据思维导图可以快速、准确地找出逻辑规律，找到解决问题的办法。同时，在学习中，学生之间可以交流思维导图，了解对方思维的方向性，从中受到借鉴与启示，不断完善问题的解决方法。

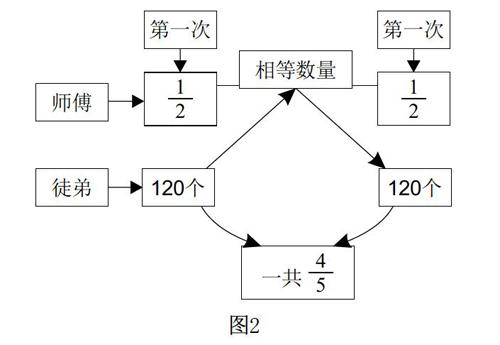
如教师出示以下习题让学生分析与解决：师傅和徒弟进行零件加工，他们各加工相同数量的零件。当师傅完成加工任务的一半时，徒弟加工了120个;当师傅完成任务时，徒弟完成了任务的4/5。师徒任务都完成后，共加工了多少个零件？分析：当师傅完成一半时，徒弟完成这批零件的2/5，也就是120个。由此得出零件的件数为120÷2/5=300个。学生对该题存在的关系进行了分析，并绘制了思维导图（如图2）。

思维导图能帮助学生理清题中已知条件与数量关系，使学生很容易找到解决问题的思路，提高数学探究能力。

4   巧用思維导图，突破学习难点

巧用思维导图可以使知识的呈现更加具体形象，给学生以形象的感知，进而突破教学的重点与难点，让学生更易于掌握知识之间的联系，深入理解知识的内涵，提高数学思维能力。

如“认识多边形”这一课涉及很多图形，如长方形、正方形、梯形和平行四边形等。处于形象思维阶段的学生特别适合直观教学，他们常常用形象、感性的形式来认知与理解事物。在一节课中了解与掌握这么多知识，对学生来说存在一定的难度。对此，教师在引导学生理解这些图形时，可以通过多媒体展示这些图形，边展示边让学生了解这些图形的名称。接着教师可让学生观察，找出这些图形的联系点，弄清这些图形之间存在怎样的联系，在边角上存在怎样的联系，有哪些相同的性质。最后教师可结合图形之间的关系绘制出思维导图，让学生明确这些图形的区别与联系。

5   巧用思维导图，培养发散思维

提高学生的创新能力是数学教学的重点。创新能力的培养仅靠做题是远远不够的，要运用思维导图促进学生发散思维的形成。

教学“圆柱和圆锥”的相关知识时，教师要引导学生回顾学过的圆柱知识，画出简单的思维导图。教师再提问：“由思维导图可知，圆柱的体积公式是V圆柱=Sh，其中的S代表圆柱的底面积，h代表圆柱的高，那么与这个圆柱等底等高的圆锥的体积是多少呢？”由此导入新课，让学生探究圆锥的体积公式。接下来，教师要引导学生利用课前分发的等底等高的圆柱与圆锥，标出圆锥的高，发现圆锥的高是圆锥的顶点到其底面圆心的距离，思考圆锥的体积与其等高等底的圆柱的体积存在怎样的关系。学生把装满圆柱的水倒向圆锥，发现圆柱内的水可以倒满三个圆锥。还有的学生将圆锥内装满细沙，再倒入圆柱，发现三个圆锥的细沙可以将一个圆柱倒满。因而学生得出圆锥的体积等于与其等底等高圆柱体积的三分之一，即

V圆锥=Sh。学生由此可以增强成就感与探究的积极性，通过思维导图的启发，在探究中运用把圆柱的水倒入圆锥的方法，或把装满圆锥的沙倒入圆柱的方法，发现用不同的思维、不同的探究方法找出解决问题的不同方法，能得出同样的结果。

总之，思维导图具有直观性，能够使学生形象地理解知识之间的联系，产生探究的动力，提高数学素养。

【参考文献】

[1]赵国庆.概念图、思维导图教学应用若干重要问题的探讨[J].电化教育研究，2018（5）.

[2]毛伟军.运用数形结合思想提高数学教学实效探研[J].成才之路，2018（17）.

[3]董泽芳.思维导图在小学高年级数学学习中的运用研究[J].教学案例，2018（23）.

[4]照慧臣，王玥.我国思维可视化研究的惠顾与展望——基于中国知网2003—2013年论文的分析[J].中国电化教育，2014（4）.

[5]张海森.2001—2010年中外思维导图教育应用研究综述[J].中国电化教育，2011（8）.