对称V型异步启动永磁同步电机齿槽转矩优化
2021-06-10李晓峰高锋阳齐晓东李昭君李浩武
李晓峰 ,高锋阳 ,,齐晓东 ,李昭君 ,李浩武
(1.兰州交通大学自动化与电气工程学院,兰州 730070;2.甘肃交达工程检测科技有限公司,兰州 730070)
异步启动永磁同步电动机LSPMSM(line-start permanent magnet synchronous motor)齿槽效应明显,运行中产生机械振动较大,在控制精度高的场合,必须减小齿槽转矩[1-3]。通过优化电机本体,调整定转子结构参数和永磁体组合可以有效降低齿槽转矩。在转子结构参数中,选择合适的转子齿倾斜角[4]、极弧系数[5]、转子齿宽[6]等可以解决齿槽转矩过大的问题,但是容易出现空载反电动势幅值减小,进而引起绕组电流偏大,电机损耗增加的问题;同时,转子磁极倾斜结构也能有效降低齿槽转矩[7],但制造难度较大,增加了加工成本在定子结构中。在定子结构方面,文献[8-9]分析了定子斜槽结构、定子槽参数对LSPMSM齿槽转矩的影响,结果表明,采用不等齿宽配合及合适的定子槽参数能降低齿槽转矩,但都未对优化后的电机电磁性能进行分析比对,优化后不能保证电机合理性;选取不同永磁体组合同样可以降低齿槽转矩,文献[10]将不同尺寸和不等体积的2种永磁体钐钴和钕铁硼组合在同一极,使气隙磁密波形更加正弦化,从而减小齿槽转矩和永磁体用量,但牺牲了部分气隙磁密,降低了转矩密度。
对单一或少数结构参数优化,能抑制齿槽转矩,但会出现损耗增加和转矩密度降低等问题。多参数同时优化可以达到降低齿槽转矩和提升电机性能的目的。传统的齿槽转矩优化方法主要利用有限元软件建模计算,多参数优化时,计算量大且耗时,难以得到齿槽转矩与电机结构参数明确表达关系。文献[11]将蚁群算法与有限元法相结合,对电机效率和永磁体用量两个目标进行优化。该方法大幅降低了计算时间和计算量,但是未考虑各个优化参数的影响权重,得到的最优值存在一定局限性。将多参数优化与智能算法相结合,可以有效提高优化效率。文献[12]通过灵敏度分析确定各结构参数对内置式永磁同步电机的转矩脉动和输出转矩的影响程度,并利用多目标粒子群算法求取最优解,优化后电机转矩脉动降低的同时输出转矩提高,但是所选取的影响参数过多,优化过程中增加了算法寻优的复杂度。
本文从降低齿槽转矩的优化角度出发,选取极弧系数、定子槽口宽度、永磁体厚度、转子轴向长度和转子齿宽5个影响参数,并通过参数敏感度分析,将优化变量分层,筛选出影响比重高的参数。以15 kW对称V型LSPMSM为研究对象,综合响应面法RSM(response surface method)与参数化扫描相结合逐层分析,利用最大-最小蚁群系统MMAS(max-min ant system)对响应面方程寻优处理,确定最小齿槽转矩下的最优参数,并结合有限元仿真实验验证了优化后电机电磁性能及效率。
1 齿槽转矩的解析分析
图1为对称V型LSPMSM电机结构,永磁体内置转子部分呈V型对称排列,齿槽转矩分析时与其他类型异步启动永磁同步电机相似。

图1 对称V型LSPMSM电机结构Fig.1 Structure of symmetrical V-type LSPMSM
在分析齿槽转矩时,假设电枢铁心磁导率无穷大,且定、转子均为矩形槽,根据文献[13-16]得其转矩表达式为

根据假设,对称V型LSPMSM磁场能量W可视为气隙能量Wgap与永磁体能量Wp之和,即

式中:V为气隙体积;μ0为磁导率;B为气隙磁密,其沿电枢表面的分布为

式中:hm为永磁体宽度;Br为剩磁;g(θ,α)为等效气隙长度。将式(3)代入到式(2)中,得


式中:ps为定子齿数;αp为极弧系数。
对于对称V型LSPMSM,结合图1,将等效气隙长度 g(θ,α)傅里叶展开得
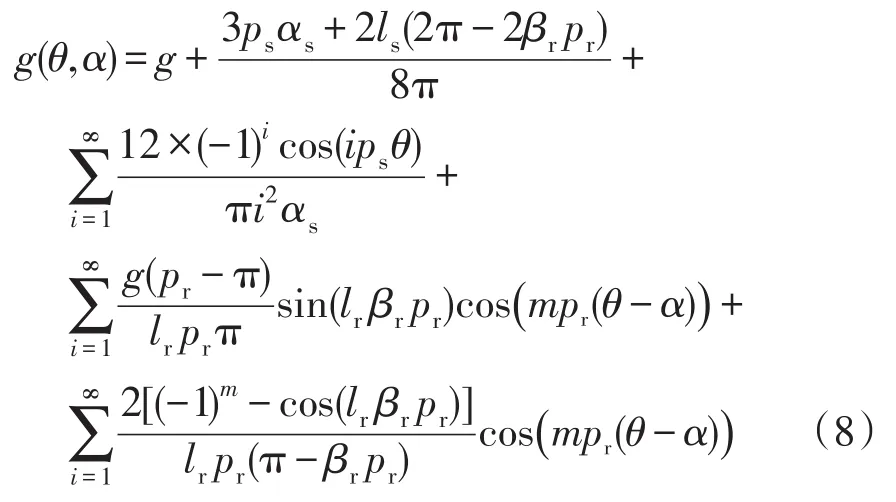
式中:αs和βr分别为定子槽口宽度和转子齿宽度;pr为转子齿数;lr为转子轴向长度;g为电机的气隙长度。
将式(5)~式(7)代入到式(4)中,再通过式(1)计算得到对称V型LSPMSM齿槽转矩,即

式中,R2和R1分别为定子内径和转子轭外径。
结合上述公式,在选择优化参数时,由于 ps、Br、g、pr在电机设计时就已确定,因此选择极弧系数αp、定子槽口宽度αs、永磁体宽度hm、转子轴向长度lr、转子齿宽 βr为最终优化参数,为方便参数优化,分别以A、B、C、D、E、表示。
2 电机优化流程


图2 对称V型LSPMSM齿槽转矩优化流程Fig.2 Cogging torque optimization process of symmetrical V-type LSPMSM
2.1 电机结构及优化参数
图3为对称V型异步启动永磁同步电机3D模型结构。该电机为15 kW,采取36槽4极整数槽分布绕组结构,转子槽数为32,主要参数如表1所示。在保证定转子槽数、定转子内外径等参数不变的情况下,对确定的参数进行优化,以达到削弱齿槽转矩的目的,根据电机设计手册[17],选择参数初值及优化范围,具体优化参数如表2所示。

表1 对称V型LSPMSM主要参数Tab.1 Main parameters of symmetric V-type LSPMSM

表2 对称V型LSPMSM主要优化参数Tab.2 Main optimization parameters of symmetrical V-type LSPMSM

图3 对称V型LSPMSM电机3D模型Fig.3 3D Model of symmetrical V-type LSPMSM
2.2 优化参数敏感度分析
参数敏感度分析用来判断各个参数对优化目标的影响程度[12],本文通过各参数变化对电机齿槽转矩幅值的影响率来表示。每个优化参数所占比例为
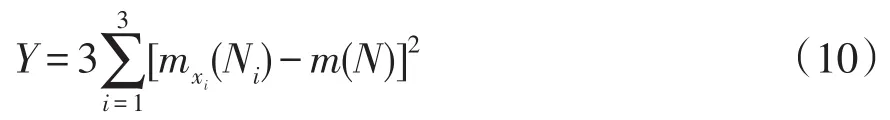
式中:Y 为每个优化参数所占比重;xi(i=A、B、C、D、E)为5个优化参数;N为对称V型LSPMSM齿槽转矩幅值;mxi(Ni)为x的第i个取值变量下N的平均值;m(N)为N的平均值。本文中优化参数分别选取3个实验点,分析优化参数对优化目标的影响程度时,建立实验矩阵,共需要32=9次仿真实验。
每个参数所占比例与所有参数比例之和的比值为影响率,图4为计算所得各参数的影响率。
从图4可以看出,对称V型LSPMSM齿槽转矩敏感度较高的3个参数为极弧系数A、定子槽口宽度B和永磁体宽度C,影响率分别为41.1%、25.3%、26.1%,将这3个参数划分为第1层;转子轴向长度D、转子齿宽E敏感度较低,影响率分别为4.3%、3.2%,划分为第2层。

图4 齿槽转矩敏感度分析Fig.4 Sensitivity analysis of cogging torque
2.3 第1层参数优化
目前,计算电机结构参数最优值主要采用有限元模拟仿真。若将多个参数同时进行优化,软件仿真计算量将会大大增加,同时耗时也呈指数增加。本文中选取5个优化参数,若每个参数选取3个水平因素,则需进行53=125次仿真,并且参数之间的相互影响易被忽略。因此,不能保证计算结果的准确性。
本文采用参数分层设计,将第1层的3个参数构建响应面方程,需采集样本点17个;第2层单变量优化仿真15次,共进行30次采样,相比于单一使用有限元软件优化,数据样本采集减少了76%,在保证优化结果准确的同时提高了优化效率。第2层参数相对于第1层参数对齿槽转矩的影响较小,在进行第1层参数优化时,第2层参数转子轴向长度D、转子齿宽E的初始值分别为190.00 mm、14.5 mm固定不变。
2.3.1 响应模型建立与分析
响应面法是一种解决多变量的统计方法,常用的实验设计有CCD和BBD两种。本文中第1层影响因素k为3个,因此选择BBD设计是十分经济的,当k˃5时,一般选择CCD设计[17-19]。优化参数与齿槽转矩之间的响应面模型为

式中:y为响应值;x为自变量;β为待定系数;ε为拟合误差。
在模型建立后,利用Design Expert10软件自动生成17个样本点,如表3所示,通过Maxwell计算得出每一组参数对应的齿槽转矩,将幅值设为响应值。参考相关电机设计方案,第1层优化参数取值范围分别定在0.60≤A≤0.75、3.6≤B≤4.0、9.3≤C≤10.3。

表3 BBD实验点齿槽转矩Tab.3 Cogging torque at experimental points based on BBD design
根据表3中的实验数据计算出拟合误差和各参数待定系数,获得对称V型LSPMSM齿槽转矩的数学模型为
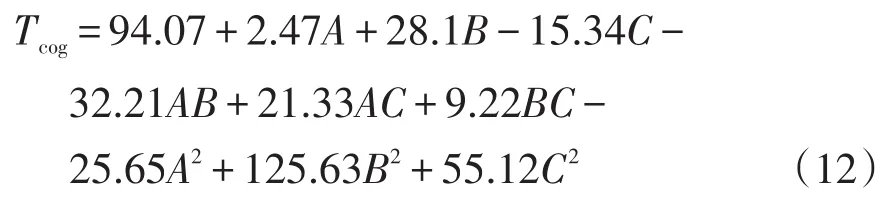
对齿槽转矩响应面模型进行方差分析,结果如表4所示。其中,R-Squared表示总的判定系数,计算结果为0.948 2,说明响应面方程拟合程度高,P与F分别表示模型的失拟项和检验系数。P小于0.001 0,说明选取的样本点均符合模型要求;F一般大于4,该模型中得到的数值为5.532,说明拟合结果符合要求。

表4 齿槽转矩响应面分析Tab.4 Response surface analysis of cogging torque
根据响应面曲面模型,可以得到对称V型LSPMSM齿槽转矩与3个参数A、B、C之间的相互关系,如图5所示。由图5(a)可知,随着定子槽口宽度逐渐增加,齿槽转矩呈现先减小后增大的变化趋势,在3.72~3.78之间的某一点,齿槽转矩值最小;在图5(b)中可以明显看出,齿槽转矩随极弧系数先减小再增大;图5(c)反映出随永磁体宽度增加,齿槽转矩先减小后增大。其中,定子槽口宽度与永磁体宽度对对称V型LSPMSM齿槽转矩影响最为明显,而且二者对其交互影响作用最大。极弧系数则影响相对前两者的影响较小。图中反映出永磁体宽度在9.5~9.9 mm、定子槽口宽度在3.70~3.78 mm之间时齿槽转矩最小,但是要得到更精确的优化后各个参数,需要进一步计算。

图5 响应曲面Fig.5 Response surfaces
2.3.2 MMAS智能算法寻优
建立RSM模型后,为了更加准确得到最小齿槽转矩时的3个参数A、B、C。本文选用MMAS进行寻优,该算法在计算中逐渐增加全局最优解的使用频率,保证了计算结果的准确可靠。
在MMAS算法中,节点i到节点j转移的概率为

式中:τij为边(i,j)上的信息素;ηij为启发式因子,ηij=1/dij;αk为蚂蚁k下一步被允许访问的节点集合[20-21]。
MMAS可以避免算法过早收敛于局部最优解,信息素的初值被设为其取值上界。因此该算法强调对最优解的利用。结合式(11)求解响应面模型最小值,从而确定第1层参数的最优值。表7为MMAS算法优化前后各参数与优化目标的结果,优化后极弧系数取0.69,永磁体宽度取9.81,定子槽口宽度取3.75 mm,通过MMAS求得齿槽转矩为98.17 mN·m,有限元验证结果为98.53 mN·m,两者结果接近,表明建立的齿槽转矩优化响应面模型准确可靠。较之于优化前齿槽转矩355.56 mN·m,优化后其幅值降低了72.4%。因此,采用响应面法与MMAS智能算法相结合的优化方法,可准确计算出对称V型LSPMSM最小齿槽转矩。

表7 MMAS算法优化结果Tab.7 Optimization results of MMAS algorithm
2.4 第2层参数优化
通过灵敏度分析可知,第2层参数灵敏度较小,可以采用有限元参数化扫描,引入优化评判标准函数,用于检验优化目标是否满足要求[11]。评判函数为


表8 第2层参数优化结果Tab.8 Parameter results after second-layer optimization
优化后,转子轴向长度D由190.00 mm减小到181.77 mm,转子齿宽E为12.3 mm,其他参数保持不变。优化目标由98.17 mN·m减小到92.46 mN·m,满足所引入的评判函数。在第1层优化的基础上,齿槽转矩幅值降低了5.81%。
3 仿真验证
为了验证所提出方法的有效性,通过Maxwell建立有限元模型,优化后的极弧系数为0.69、定子槽宽度为3.75 mm、永磁体宽度为9.81mm、转子轴向长度为181.77 mm、转子齿宽为12.30 mm。在空载且转速达到稳定1 500 r/min的情况下,得到电机A相的反电动势如图6所示,波形并非规则正弦波,由于异步启动永磁同步电机定转子双边开槽,齿槽效应明显,选铁心为DW315_50,永磁体为NTP264H,存在高次谐波。电机空载反电动势幅值大约为58.5 V,满足设计要求。

图6 空载反电动势Fig.6 No-load back EMF
空载气隙磁密的对比和傅里叶分析分别如图7和图8所示。优化前后齿槽转矩仿真波形如图9所示,可见,优化前幅值为355.56 mN·m;优化后幅值为92.46 mN·m,降低了大约73.9%,主要因为电机优化参数的改变会使气隙之间的磁导率发生改变,能有效改善气隙磁路。齿槽转矩是转矩脉动的主要来源,削弱齿槽转矩能有效降低转矩脉动[12]。图10为优化前后对称V型LSPMSM的转矩,由于启动时转矩较大且不稳定,选取了从40 ms开始转矩趋于稳定时的波形进行对比,优化后的波动明显变小,转矩脉动从16.7%下降到6.6%,从而使电机在运行时振动和噪声降低,运行情况更加稳定。

图7 空载气隙磁密对比Fig.7 Comparison of no-load air-gap magnetic density
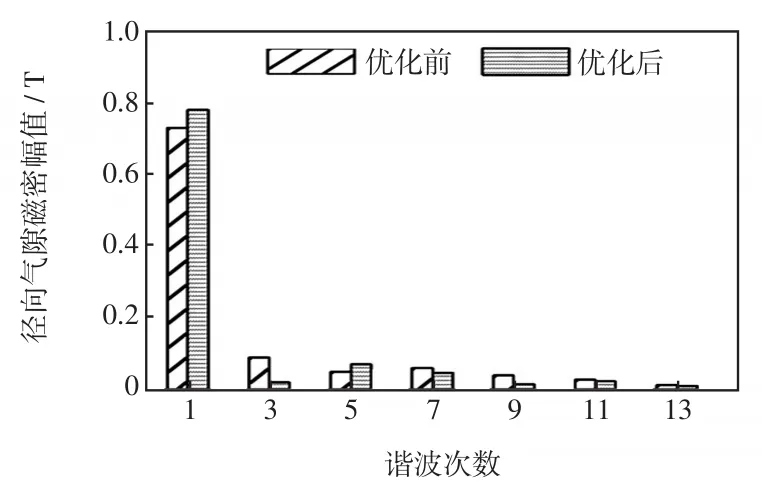
图8 空载气隙磁密傅里叶分析Fig.8 Fourier analysis of no-load air-gap magnetic density
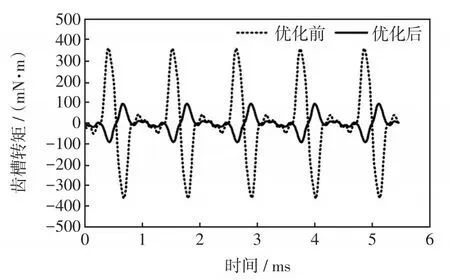
图9 优化前后齿槽转矩Fig.9 Cogging torque before and after optimization
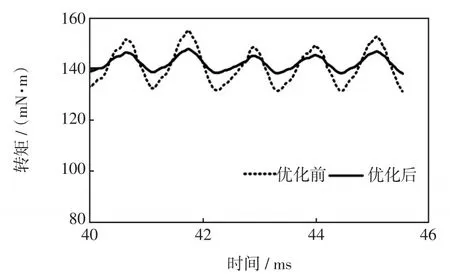
图10 优化前后转矩对比Fig.10 Comparison of torque before and after optimization
优化前后电机效率如图11所示,可见,在额定功率15 kW时,电机的效率最高;经过有限元软件分析计算,优化前电机效率为94.4%;优化后则为95.9%,优化后齿槽转矩下降的同时,电机效率也得到了提升。
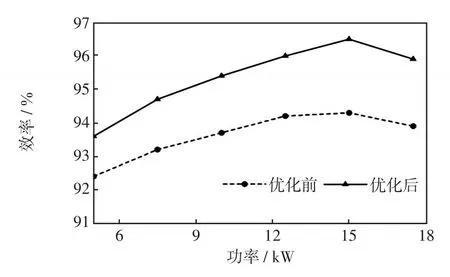
图11 优化前后电机效率Fig.11 Motor efficiency before and after optimization
综上,优化后齿槽转矩大幅削弱,电机转矩脉动也随之减小,运行更加稳定,电机电磁性能满足要求,同时较优化前电机效率得到提升,说明所提出的针对对称V型LSPMSM齿槽转矩优化方法是有效的。
4 结论
本文提出一种基于参数分层设计与响应面法相结合的对称V型LSPMSM齿槽转矩优化方法,通过MMAS算法和有限元法计算出最优参数,达到削弱齿槽转矩的目的。利用有限元分析法对优化前后电机性能进行验证,得到以下结论。
(1)参数分层与响应面法相结合显著提升了电机齿槽转矩的优化效率,与传统优化方法相比,能更加快速、准确地获取优化参数值。
(2)对电机结构参数优化能大幅削弱齿槽转矩,减小转矩脉动,从而使电机振动噪声降低。
所提出的方法能有效抑制对称V型LSPMSM齿槽转矩偏大问题,但是最终的优化参数为齿槽转矩最小情况下得到的,不能保证其他性能最优,同时该方法针对单一目标优化,具有一定的局限性,对电机的多目标优化还需要进一步研究。
