分数槽集中绕组的ISG电机涡流损耗分析

2021-06-10王晓远王力新

电力系统及其自动化学报 2021年5期

王晓远，王力新

（天津大学电气自动化与信息工程学院，天津 300072）

集成启动发电机ISG（integrated started genera⁃tor）系统因其成本低、技术结构简单而被广泛应用于混合动力汽车。ISG电机综合了启动和发电的功能。在汽车加速时，电机工作在电动状态，助力发动机，弥补发动机的转矩不足。在汽车减速和制动时工作在发电状态，将能量存储在直流供电系统中[1]。ISG电机的应用场合决定了其具有功率密度大、调速范围宽、可靠性高和轴向长度短等特点。分数槽集中绕组能缩短线圈周长和绕组端部的伸出长度，因此适用于ISG系统。分数槽集中绕组的电枢反应磁动势除基波外，还存在着幅值接近基波、转向和基波相反的次谐波和高次谐波磁动势[2]。谐波磁动势相对转子有较高的转速，会在永磁体内产生大量的涡流损耗，导致永磁体温度升高。永磁体温升过高可能导致永磁体退磁，降低电机的可靠性[3]。此外，分数槽集中绕组ISG电机工作环境恶劣，散热条件差，因此有必要研究降低ISG电机永磁体涡流损耗的方法。

国内外学者对于永磁体的损耗进行了一系列的研究。文献[4]提出了一种判断不同极槽配合下定子磁动势谐波对转子损耗的影响因子，该因子越大转子损耗越大，并通过有限元验证了分析方法的有效性；文献[5]分析了分数槽集中绕组表贴式永磁同步电机转子损耗，得出了在低速区间转子损耗以铁心损耗为主、在高速区间转子损耗以永磁体涡流损耗为主的结论；文献[6]分析了变频器供电条件下的定子槽口宽度对永磁体涡流的影响，得到减小定子槽口宽度能有效减小永磁体涡流损耗的结论；文献[7]分析了永磁电机转子涡流损耗的产生机理，并提出了利用转子轭和永磁体分段技术降低涡流损耗；文献[8]研究了一种基于分数槽集中绕组的新型绕线形式，大大减少了绕组磁动势的次谐波，从而减少了永磁体的损耗；文献[9]研究了一种新型转子结构，通过增加阻尼环降低了永磁体的涡流损耗。

定子开槽引起的气隙磁导变化是造成永磁体涡流损耗的主要原因之一[10]。电机设计时通常将槽肩角设计较大，避免定子齿尖处的饱和。在槽满率过高的情况下需要较小的槽肩角来增加槽面积，此时槽肩高的设计直接影响定子的齿尖饱和程度。鲜有文献研究槽肩角较小时槽肩高对永磁体涡流损耗的影响。本文通过分析开槽引起气隙磁导率变化的原理，进一步研究槽肩高对永磁体涡流损耗的影响，总结了定子槽肩高设计原则，为工程设计提供了一定借鉴。

1 定子开槽引起气隙磁导率变化的解析计算

1.1 样机参数

以一台50 kW电动汽车用ISG电机为研究对象。定子绕组采用分数槽集中绕组形式以节省端部用量，缩短电机轴向长度。极槽配合选择18槽12极，转子形式为内置一型。电机的径向截面如图1所示。单元电机为2极3槽形式，其主要设计参数见表1。

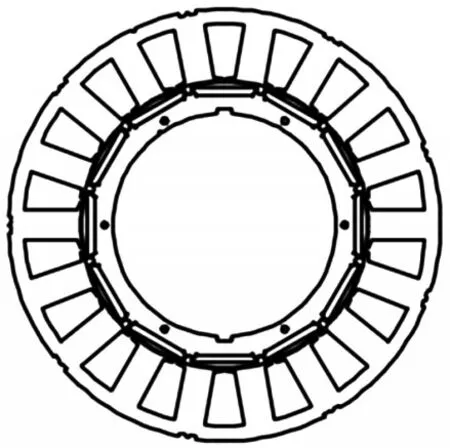
图1 ISG电机的径向截面Fig.1 Radial cross-section of ISG motor

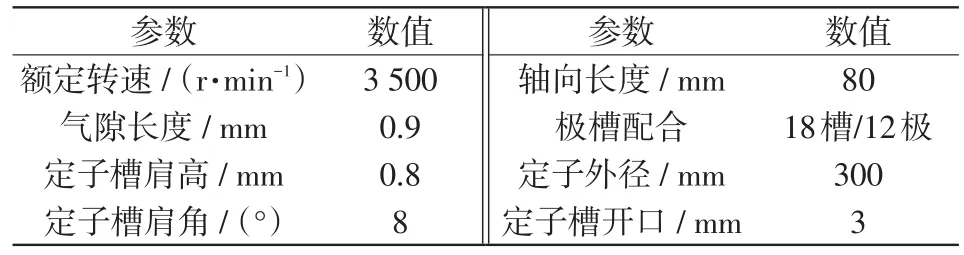
表1 ISG电机的主要设计参数Tab.1 Main design parameters of ISG motor

1.2 定子开槽引起气隙磁导率变化的解析计算

当电机旋转时，永磁体上的任意一点从面对齿顶转到面对齿槽的过程中，磁路的磁导率会发生变化。永磁体内的磁场发生变化，感应出电动势造成涡流损耗[11]。因此，减少定子开槽引起的气隙磁导变化可以减少永磁体涡流损耗。

首先给出一个齿距气隙磁密的计算模型[10]，如图2所示。考虑到计算模型的复杂性，做出如下假设：铁心的磁导率远大于空气磁导率；除铁心外的非导磁材料的磁导率和空气磁导率相同；在二维平面求解，忽略轴向长度的影响。

图2 定子开槽对气隙磁密影响的计算模型Fig.2 Calculation model of the influence of stator slotting on airgap magnetic density

由Cater理论，电机槽开口对高次谐波的影响解析分析为

1个齿距内气隙磁通密度的变化情况可以表示成傅里叶形式，即

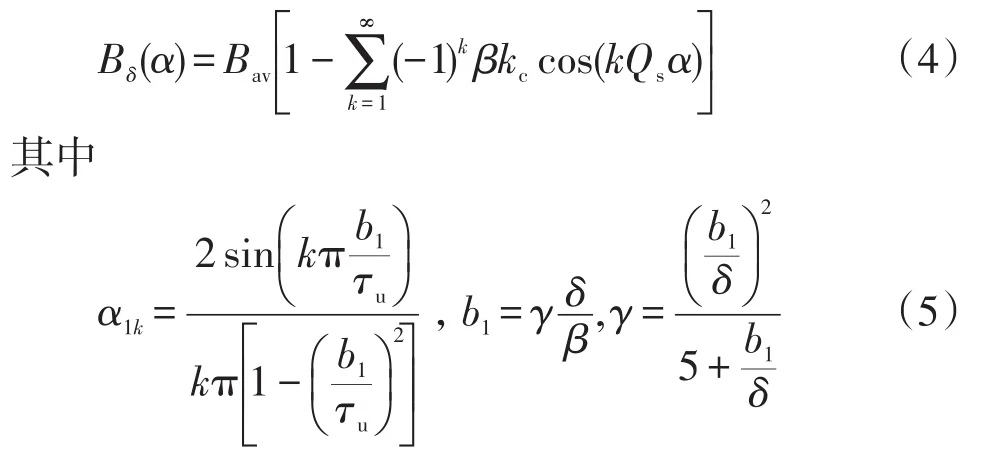
由上述各式可以得到

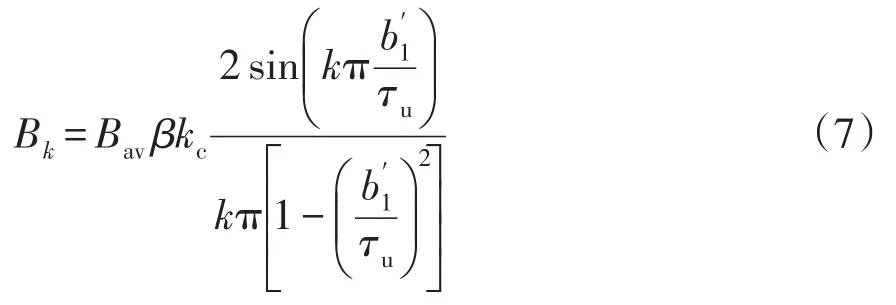
式中：Bk为定子槽口影响下的k次谐波幅值；τk为k次谐波的波长。

由式（7）计算ISG电机的气隙磁密谐波畸变率理论值为26.1%。电机设计中减小槽口可以降低气隙磁密的畸变，从而减低永磁体涡流损耗。但定子槽口过小会导致电机下线困难甚至无法下线，增加了电机制造的成本。

1.3 考虑铁心饱和的气隙磁密

上述分析定子槽开口对气隙磁密影响时，忽略了定子齿尖的铁磁材料非线性，认为铁磁材料的磁导率远大于空气磁导率。实际电机中若存在定子齿尖严重饱和，则必须考虑铁心材料的非线性而引起的铁磁材料磁导率的下降。以研究对象ISG电机为例，槽肩角设计为8°，槽肩高为0.8 mm，空载下电机气隙磁密波形以及气隙磁密云图如图3所示。

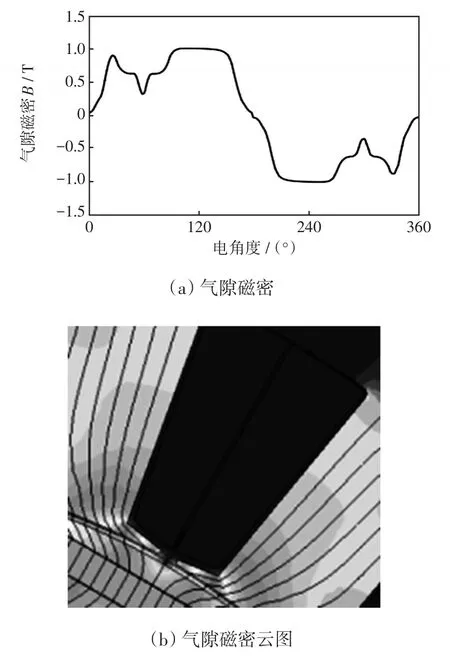
图3 定子槽肩角8°的空载气隙磁密波形及云图Fig.3 Airgap magnetic density waveform and cloud chart under no-load condition at stator slot shoulder angle of 8°

气隙磁密畸变率为27.7%，高于不考虑饱和的理论计算值26.1%。由于铁磁材料的非线性，定子齿尖磁导率会随着饱和程度的上升而下降。气隙磁密出现了两段式的下降，当磁动势经过定子齿尖会遇到较高的磁阻，磁密小幅度下降。磁动势经过槽口，遇到了空气磁阻，磁密将大幅度下降。气隙磁密的两段式下降，增加了气隙磁密的谐波含量。

2 定子槽肩高对永磁体涡流损耗的影响

2.1 槽肩高对永磁体涡流损耗的仿真计算

增加槽肩高和增大槽肩角是抑制定子齿尖饱和的有效手段。增大槽肩角会导致槽面积严重下降，当ISG电机槽肩角增大至30°时，槽面积降低6%，已无法满足下线的工艺性。保持槽肩角度并增加槽肩高能在槽面积变化很小的情况下抑制定子齿尖的饱和。为了探究定子齿尖饱和情况下定子槽肩高对永磁体涡流损耗的影响，建立ISG电机的有限元仿真模型，利用有限元法计算永磁体涡流损耗，仿真模型如图4所示。

图4 ISG电机的1/6有限元仿真模型Fig.4 1/6 FEA simulation model of ISG motor

对求解模型做如下假设：①不考虑永磁体充磁的不均匀性；②铜线的导磁率接近于空气；③以定子外径处的空气包为计算边界条件，假设电机场量全部包含在空气包内，空气包外的磁场为0；④不考虑端部效应，使用二维仿真模型求解。

取气隙平均半径处的圆作为观测路径，求解空载情况下，定子槽肩高为0.8、1.2、1.5、1.8、2.0、2.2、2.5 mm的有限元模型。不同槽肩高下的空载气隙磁密B及傅里叶分解结果如图5所示。

仿真结果支持理论分析。图5（a）可以看出，在槽肩高小于1.8 mm的时，空载气隙磁密存在两段式下降，这是由于定子齿尖存在饱和导致的。在槽肩高大于1.8 mm以后，气隙磁密不存在明显的两段式下降，气隙磁密只变化了1次。

气隙磁密进行傅里叶分解结果如图5（b）所示。可见，基波随槽肩高的增加而增大，最主要的3次谐波随槽肩高的增大而逐渐减小；5次谐波和11次谐波在槽肩高小于1.8 mm时随槽肩高的增加明显变小，在槽肩高大于1.8 mm后不再变化；7次谐波随槽肩高的变大先减小后变大，在槽肩高为1.8 mm时最小；9次谐波和15次谐波基本不随槽肩高的变化而变化，而13次谐波随槽肩高增大而略微增大；磁密谐波的减少，也使得基波值有所增大。不同槽肩高的波形畸变率如表2所示。

图5 不同槽肩高下空载气隙磁密波形以及傅里叶分解结果Fig.5 Airgap magnetic density waveform and Fourier decomposition result under no-load condition at different slot shoulder heights

表2 不同槽肩高的空载气隙磁密波形畸变率Tab.2 Distortion rate of airgap magnetic density waveform under no-load condition at different slot shoulder heights

由计算得到的空载气隙波形畸变率，结合前文的理论分析可以预见，增大槽肩高可以有效减小永磁体的涡流损耗。应用有限元仿真，求解ISG电机1个周期的单块永磁体涡流损耗。不同槽肩高情况下转子永磁体涡流损耗的有限元分析结果如图6所示。

图6 不同槽肩高下的单块永磁体涡流损耗Fig.6 Eddy current loss in one single permanent magnet at different slot shoulder heights

从图6可以看出，在定子槽肩高为0.8 mm时，磁密高次谐波作用在定子铁心和永磁体上产生了大量的损耗；当定子槽肩高为1.8 mm时，定子齿尖饱和程度下降，气隙磁密高磁谐波含量减小，永磁体损耗降低；定子槽肩高继续增加时，齿尖磁导率远大于空气磁导率，气隙磁密不再发生明显变化；当定子槽肩高为2.5 mm时，永磁体涡流损耗已下降得不太明显。这与之前的理论分析一致。当槽肩高从0.8 mm增加到1.8 mm时，槽满率仅增加1.75%；永磁体涡流损耗由97.58 W下降至75.60 W，下降了22.60%。

2.2 定子槽肩高的设计原则

前文分析了定子槽肩高对永磁体涡流损耗的影响，并应用有限元法对ISG电机进行了求解分析。分析结果表明，在定子齿尖铁磁饱和的条件下，增加槽肩高能有效减小永磁体的涡流损耗。且槽肩高在大于某值时，永磁体涡流损耗下降不再明显。因此需要总结定子槽肩高的设计原则。另选2台电机，对其空载气隙磁密波形进行分析，探究槽肩高的设计最佳值。不同电机的气隙磁密对比如表3所示。

表3 不同电机的气隙磁密对比Tab.3 Comparison of airgap magnetic density waveform among different motors

由仿真结果可以总结，分数槽集中绕组的定子槽肩高的设计原则为

式中：ho1为槽肩高；δ为气隙长度。

3 实验验证

为了验证仿真结果的可靠性和电机设计的准确性，试制了2台样机。由于槽肩高为1.8 mm时电机槽满率过高，定子下线存在困难，因此选择2台样机的槽肩高分别为0.8 mm和1.5 mm，进行电机的实验。图7为样机实验平台。

图7 样机实验平台Fig.7 Experimental platform of prototype

空载反电动势的波形畸变率很大程度上反映了气隙磁密的波形畸变率。空载反电动势最容易通过实验验证，基于实验仪器条件，分别对2台样机的空载反电动势进行实验测试。因永磁体涡流损耗难以直接通过实验获取，通过实验获得的反电动势结果，再应用反电动势下降法[10]间接获取ISG电机的永磁体涡流损耗。

2台样机在额定转速下的线空载反电动势实测与仿真波形如图8所示。可见，槽肩高为0.8 mm时，空载反电动势的基波幅值的实验结果为355.5 V，仿真结果为370.4 V；实验和仿真的波形畸变率分别为5.20%和7.14%。槽肩高为1.5 mm时，空载反电动势的基波幅值实验结果为356.2 V，仿真结果为372.0 V；实验和仿真的波形畸变率分别为3.31%和3.92%。