高速电机系统电感对电磁损耗抑制效果的敏感度分析

王晓远，蔚 盛，陈学永

（1.天津大学电气自动化与信息工程学院，天津 300072；2.天津内燃机研究所，天津 300072）

高速永磁同步电机HSPMSM（high-speed per⁃manent magnet synchronous motor）采用控制器供电，控制器输出的电流时间谐波会加剧电机的电磁损耗，对电机的效率和可靠性产生负面影响[1-2]。由于高速永磁同步电机通常具有电磁气隙大、匝数少的特点，导致其电枢电感较小，对电流时间谐波的抑制能力有限，故常采用串联电抗器的方式增大系统电感以抑制电磁损耗，此时系统电感包括电枢电感和电抗器电感两部分。系统电感增加的同时会对电机动态性能产生负面影响，因此有必要对电机在不同系统电感下的电磁损耗做计算，分析系统电感对电磁损耗抑制效果的敏感度，选择最优的电抗器电感。

国内外学者对控制器供电时的电流谐波以及电磁损耗计算及其抑制方法进行了一系列的研究。文献[3]采用场路耦合仿真的方式对比了变频器供电与正弦波供电的情况，仿真了载波比和调制比对电机损耗削弱效果的影响；文献[4]针对一台涡轮鼓风机用高速电机，对转子护套进行了分段设计，对护套分段并优化涡流通路，计算并对比了优化前后的损耗变化；文献[5]以一台非晶合金永磁同步电机为例，研究了不同控制策略下的铁耗分布规律；文献[6]针对非正弦供电下的永磁同步电机，提出一种用于评估电枢磁动势谐波对转子涡流损耗影响的损耗因子，评估电流时间谐波对转子涡流损耗的影响；文献[7]针对表贴式高速永磁同步电机永磁体中的涡流损耗进行了谐波分析，计算了电机变频器载波引起的涡流损耗，提出了利用磁钢分段优化转子涡流损耗的方法；文献[8]以一台高速永磁同步电机为例，计算力气隙长度、槽开口宽度以及护套材料对于转子涡流损耗的影响；文献[9]提出一种新型的无刷直流电机矢量控制策略，抑制了电流时间谐波并减小了电机中的电流波动程度。

为了分析系统电感对电磁损耗的影响，首先对电枢电感进行计算。电机采用永磁实心转子，相对于转子轴穿过永磁体的结构，电枢反应产生的磁场分布特点有较大不同，故在计算电枢电感时应结合其结构特点特殊考虑。串联电抗器可以有效抑制电磁损耗，但要综合考虑系统电感对不同电磁损耗抑制效果的敏感度做最优选择，鲜有文献对电抗器的最优选取原则做分析。通过场路耦合仿真计算系统电感对不同电磁损耗抑制效果的敏感度，为类似工程设计提供借鉴。

1 高速电机电枢电感的解析计算

1.1 电机结构与参数

转子结构如图1所示。转子由实心永磁体、护套、和转子轴组成，其中：永磁体采用钐钴材料，具有温度系数低、最大失效温度点高的特点；护套采用镍基高温合金材料，在高温下仍旧具有很高的强度；转子轴由左右两个半轴组成，采用气浮轴承支撑转子运转。

图1 高速永磁同步电机转子结构Fig.1 Rotor structure of HSPMSM

定子铁心和绕组结构剖面如图2所示。采用2极12槽配合；为降低铁耗，铁心由0.2 mm厚的硅钢片叠成，且设计磁密较低；为削弱集肤效应影响，绕组采用多根导线并绕。电机主要结构尺寸如表1所示。

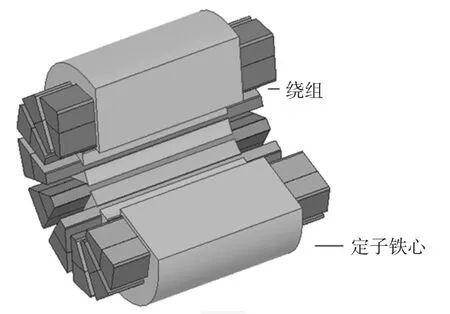
图2 高速永磁同步电机定子结构Fig.2 Stator structure of HSPMSM

表1 高速永磁同步电机的主要设计参数Tab.1 Main design parameters of HSPMSM

1.2 电枢反应电感计算

电枢电感包括电枢反应电感、槽漏电感、端部漏电感3部分。采用解析的方式，结合两极永磁实心转子电机的结构特点，首先对电枢反应电感进行计算。

采用磁链法计算电机的电枢反应电感。假设在对称的三相绕组中通入对称的三相电流，以电枢磁动势基波过零点为坐标起始点，如图3所示，对于两极永磁实心转子高速电机，空间电角度与空间机械角度相同，电枢磁动势基波分布函数F(θ)为

式中：N为一相串联匝数；I为相电流的有效值；ky1为短距系数；kq1为分布系数；θ为空间机械角度。

为计算电枢反应电感，需计算电枢电流单独作用时的等效气隙长度和绕组交链的磁链。由于永磁体和护套的磁导率接近真空，故将转子上的励磁源永磁体去掉，并将永磁体和护套所在区域用真空代替，仅保留电枢电流作为励磁源。

由于转子为永磁实心转子，转子中不含导磁轴。当电枢电流单独作用时，等效气隙区域以及该区域内的磁力线分布如图3中虚线所围区域所示。电枢磁动势产生的磁场从一个极出发直接回到另一极，位于不同θ处的磁力线穿过气隙区域的距离不相同，靠近圆心位置的距离较长，靠近两端位置的距离较短，等效气隙长度不是一个固定值，应该计算气隙长度在不同位置处的函数表达式。

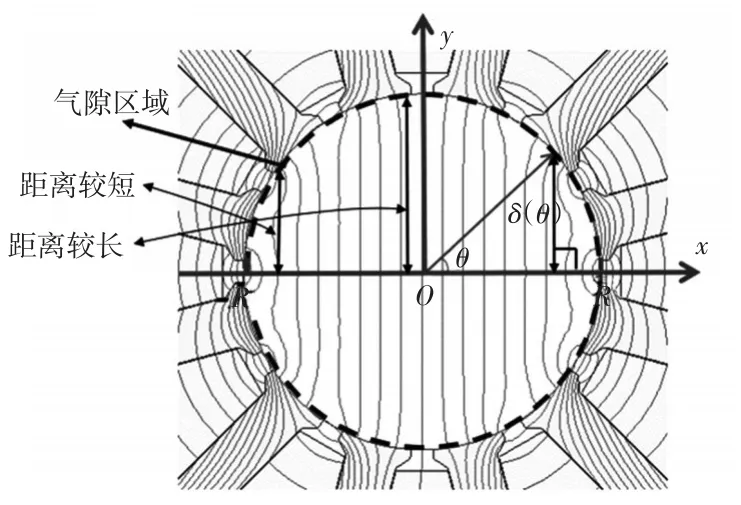
图3 电流建立的磁场以及等效气隙长度δ（θ）Fig.3 Magnetic field established by current and equivalent air gap length δ（θ）

图3中，在电机的一个极下，当θ取值为0°和180°时，气隙等效长度为0；当θ取值为90°时，气隙等效长度为R。不同位置处的气隙长度δ（θ）与θ之间的关系为

则电机在单位轴向长度上的气隙磁导在该坐标系下的分布函数为

式中，μ0为真空磁导率，μ0=4π×10-7H/m。

由于电枢磁动势基波F（θ）和单位轴向长度上的气隙长度Λ(θ)均为θ的函数，在计算绕组交链的磁链时，需要采用积分法，首先计算位于空间中每个位置x处的微元交链的磁链，然后在[-R，R]范围内对磁链进行积分，得到每相绕组交链的基波磁链为

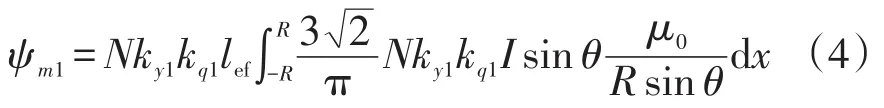
利用磁链和电流幅值的比值计算电机的电枢反应电感，得到最终电机电枢反应电感[9]为

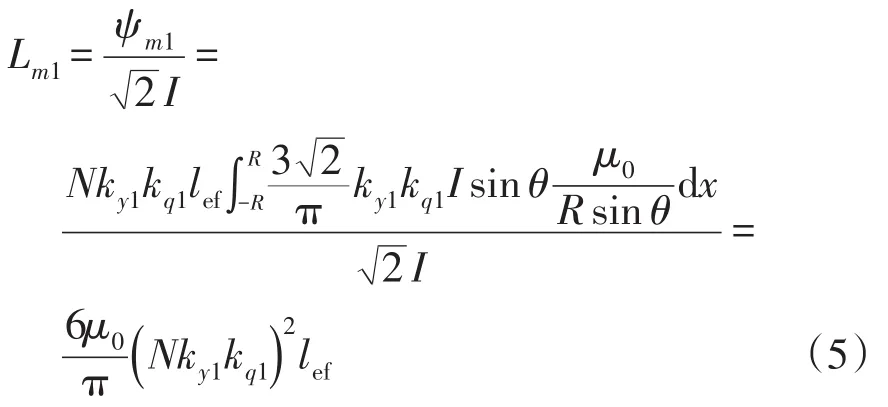
式中，lef为绕组有效部分的长度。

1.3 槽漏电感和端部漏电感计算

电机的槽漏电感与端部漏电感的计算方式与常规电机相同，双层绕组的槽漏电感的表达式[10]为

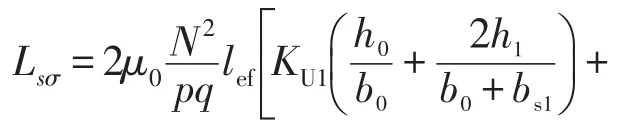
式中：KU1和KL1分别为上下层的节距漏抗系数；b0、bs1、bs2和h0、hs1、hs2为定子槽型形状的参数，取值如表2所示。定子槽型形状参数示意如图4所示。

表2 定子槽形参数Tab.2 Parameters of stator slot

图4 定子槽型参数示意Fig.4 Schematic of parameters of stator slot

在双层短距绕组中，端部漏电感[10]为

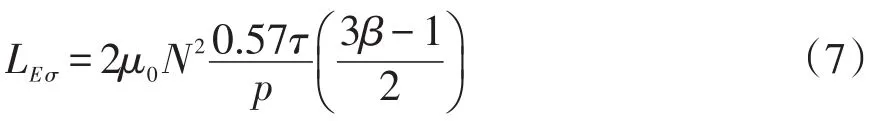
式中，τ为电机极距。

计算得到电枢反应电感为36.92 μH，槽漏电感为3.01 μH，端部漏电感为1.73 μH。当存在外部电抗器时，整个系统的电感为

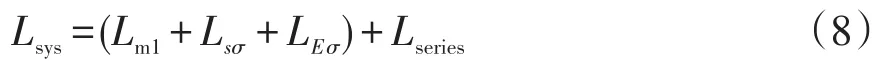
式中：Lsys为系统电感；Lseries为电抗器电感。

2 系统电感对电磁损耗抑制效果的敏感度分析

2.1 电机与控制器直接连接时的电磁损耗分析

计及时间谐波的影响，考虑每个工作状态下开关管的开关过程、将控制电路和电机本体模型耦合在一起仿真计算[13]。电机与控制器直接连接时的模型如图5所示，直流侧电压为540 V，控制器输出SVPWM对电机供电，采用的载波频率为20 kHz，电机工作频率即调制波频率为1 kHz。

图5 控制器与电机直接连接时的仿真模型Fig.5 Simulation model for the direct coupling of controller and motor

在无外部电抗器的情况下，此时的系统电感为电机的电枢电感，各类电磁损耗仿真结果如图6所示，转子涡流损耗平均值为101.1 W，定子铁耗的平均值为179.5 W，绕组铜耗平均值为12.3 W。

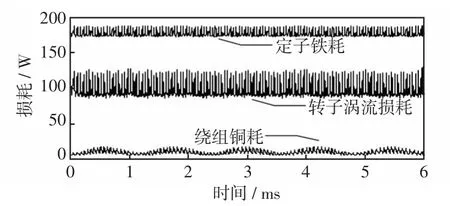
图6 控制器与电机直接耦合时的电磁损耗仿真结果Fig.6 Simulation results of electromagnetic loss when the controller and motor is coupled directly

由于电流中的时间谐波含量很大，电流波形畸变率高，造成的电磁损耗很明显，此时电机效率仅为85.3%，故由此产生的电磁损耗若不加抑制，会对电机的安全性和效率带来显著的负面影响，故需要经过串联电抗器增加系统电感对损耗进行抑制。

2.2 系统电感对电磁损耗抑制效果的敏感度分析

电机串联电抗器后，系统的电感包括电枢电感和电抗器电感两部分。系统电感增加时，由于电流时间谐波被进一步削弱，转子涡流损耗、定子铁耗、绕组铜耗相对于图6中损耗的计算结果均会得到抑制。

为了分析系统电感在增加过程中对3类电磁损耗的抑制敏感度，采用场路耦合方式，每增加25 μH的电抗器电感采用有限元法计算各类电磁损耗。如图7所示为电机、电抗器、控制器三者耦合的仿真模型示意。

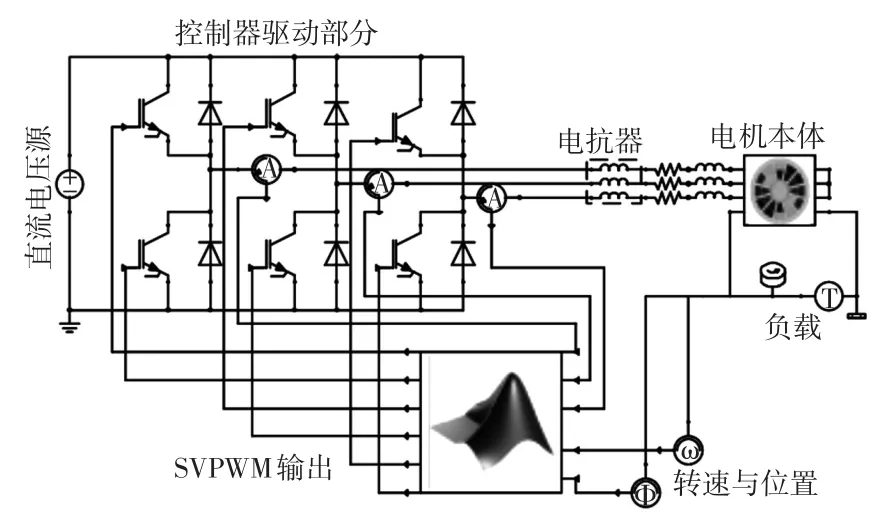
图7 电机串联电抗器与控制器耦合时的仿真模型Fig.7 Simulation model of motor series reactor coupled with controller

图8～图10所示分别为电机转子涡流损耗、定子铁心铁耗、绕组铜耗随着电抗器电感的变化曲线。

图8 转子涡流损耗随电抗器电感的变化Fig.8 Eddy current loss of rotor varying with the inductance of inductor

图9 铁耗随电抗器电感的变化Fig.9 Iron loss varying with the inductance of inductor

图10 铜耗随电抗器电感值的变化Fig.10 Copper loss varying with the inductance of inductor

由损耗的变化曲线分析可知：当滤波电抗器电感为50 μH时，与无电抗器时相比，转子涡流损耗下降了62.8%，铁耗下降了21.1%，铜耗下降了49.4%；当滤波电抗器电感为100 μH时，与电抗器电感为50 μH相比，转子涡流损耗下降了35.6%，铁耗下降了5.6%，铜耗下降了14.2%；当滤波电抗器电感为150 μH时，与电抗器电感为100 μH相比，转子涡流损耗下降了20.4%，铁耗下降了2.2%，铜耗下降了5.2%；当滤波电抗器电感为200 μH时，与电抗器电感为150 μH相比，转子涡流损耗下降了8.5%，铁耗下降了0.76%，铜耗下降了2.4%。由此分析可以得知，在系统电感增加的过程中，转子涡流损耗受系统电感变化的影响是最敏感的，其次是铜耗，而铁耗对系统电感增加最不敏感。

当外部电抗器选择200 μH时，即系统电感为240.962 μH时，各类电磁损耗随着系统电感的增加不再发生明显变化，与控制器和电机直接连接的情况相比，转子涡流损耗下降了82.6%，铜耗下降了59.9%，铁耗下降了27.6%，此时若再增加电抗器的电感，反而会影响电机的动态性能。从损耗抑制和电机动态性能两方面考虑，这是一个合适值。

3 仿真与实验验证

为了验证系统电感增加对损耗抑制的有效性，选择200 μH的电抗器，结合电磁损耗的仿真计算结果，利用有限元稳态热仿真，对电机的温度进行仿真计算和实验验证。

电机运行过程中除了电磁损耗外，还会在转子表面产生风摩损耗。风摩损耗的计算公式为

式中：Cf为绕组为摩擦系数；ρ0为介质的密度；ωm为转子角速度；r为转子半径；L为轴向长度。

将仿真计算得到的电磁损耗和风摩损耗作为电机温度场分析的热源，计算得到电机在各位置处的温度分布如图11～图13所示。

图11 转子温度串联电抗器前后变化Fig.11 Variation in rotor temperature before and after the series connection of reactor

图12 定子温度串联电抗器前后变化Fig.12 Variation in stator temperature before and after the series connection of reactor

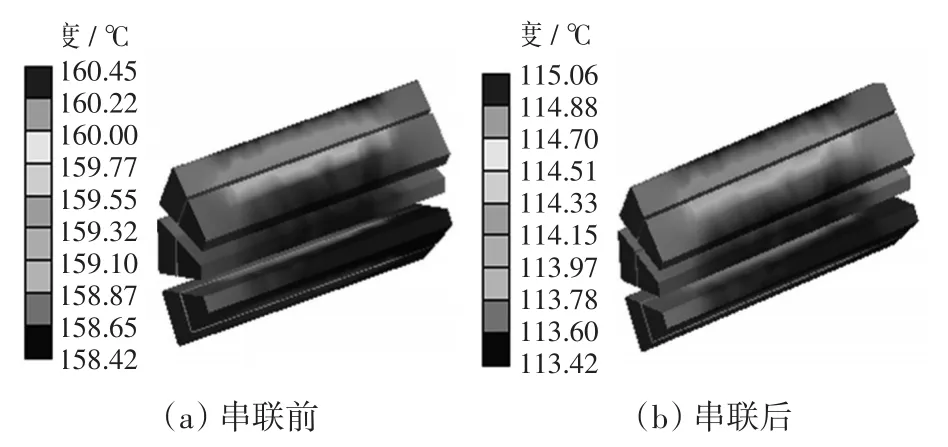
图13 绕组温度串联电抗器前后变化Fig.13 Variation in winding temperature before and after the series connection of reactor

图14所示为实验平台，对电机串联电抗器前后分别进行测试，图15为串联200 μH电抗器前后电机绕组中间和绕组端部的温度变化。

图14 实验平台Fig.14 Experimental platform

将图15中串电抗器前后电机温度达到稳定时的实测值与仿真计算值均列于表3中，由实测结果和仿真结果的对比可知，最大误差为5.05%，验证了损耗仿真结果的可靠性。

图15 电机串联电抗器前后温度变化Fig.15 Variation in motor temperature before and after the series connection of reactor

表3 温度仿真值与实测值的比较Tab.3 Comparison between simulated and measured temperatures

4 结语

采用解析法结合两极高速永磁同步电机的结构特点计算了电机的电枢电感，通过有限元仿真的方式计算了电机在与控制器直接连接情况下的电磁损耗，分析了通过外部串联电抗器使系统电感增加时各类电磁损耗对系统电感变化的敏感度，通过实验对仿真进行了验证。研究结果表明，转子涡流损耗对系统电感的变化最敏感，铜耗次之，铁耗对于对系统电感的变化最不敏感；当系统电感增大到一定值时，3种电磁损耗都不再随着电感的增加产生明显变化。分析系统电感对损耗抑制效果的敏感度，可以为选取合适的外部电抗器数值提供参考。