基于PCA-BP神经网络的审计风险识别研究

2021-06-10张志恒

重庆理工大学学报(自然科学) 2021年5期

张志恒，李超

（重庆理工大学会计学院，重庆 400054）

现代风险导向审计围绕审计风险开展审计实践活动，要求将有限的审计资源集中在高风险环节，合理配置资源，以提升审计效率和效果。这就需要对审计风险进行准确的识别和评估。大数据时代背景下，审计师在审计实务工作中所面对的信息和数据复杂多样，如何在海量复杂的数据中准确识别审计风险，提升识别准确率，是当前审计领域需要解决的重要问题。

目前，对于审计风险的研究囊括审计风险成因、影响因素以及方法评估等领域，有学者关注审计风险所包含的固有风险和控制风险［1］，并研究了影响审计风险的相关因素，包括审计师的行业了解度［2］、审计人员职业道德［3-4］等，还有研究者实证分析组织管理能力［5］、外部环境和事务所内部控制［6］、审计师经验判断［7］对审计风险的影响，并对审计风险的成因进行阐述［8］。随着互联网的发展，有研究引入大数据因素［9］。在审计风险的识别与评估方法上，有学者采用业绩归因法［10］、GONE理论分析［11］、熵权理论-层次分析法［12］、模糊综合评价法［13-14］、Python爬虫［15］及孤立点算法［16］进行学术研究。

现有的审计风险识别研究较多地使用模糊综合评价法和层次分析法，针对特定公司获取其公开和非公开的财务及非财务信息，在已有财务数据的前提下，还需根据审计对象的不同进行评价项目的制定，工作量大、多定性成分的指标，而且评价量表在更换审计对象后需要重新制定，泛化能力差。BP神经网络作为一种分类和预测方法，通过神经网络建立特征属性与识别对象间的联系来进行分类预测，该方法效果良好，被广泛应用于财务金融等领域［17-20］，但在审计风险识别领域缺乏应用。并且，由于审计风险影响因素多，各个影响因素间存在较强的相关性，若直接输入到BP神经网络模型中可能导致过拟合，影响识别效果，所以采用主成分分析方法（PCA）进行数据精简和降维处理，选取出不相关、包含绝大部分信息的主成分输入神经网络，提升模型识别效率。

基于以上缘由，利用上市公司披露的财务与非财务数据，采用PCA-BP神经网络方法构建审计风险识别模型。研究表明：该审计风险模型识别准确率高，能为审计实务工作提供有效帮助。

1 PCA-BP神经网络审计风险识别模型构建

1.1 相关理论

1.1.1 PCA方法

PCA（主成分分析）分析法由Karl Pearson提出，用于多维数据处理，通过引入正交变换，对多维信息数据进行降维转换，重新组合为新的互相无关的综合变量，实现精简指标、删除多余信息、解释主要成分的目的。PCA分析具体原理和步骤如下：

步骤1定义原始矩阵。设P个指标组成变量X，X=（X1，X2，…，Xp），其中P代表评价指标数；该变量中，样本个数为N，表示待评价的审计风险样本个数。原始矩阵计算公式为：

步骤2计算相关系数矩阵。

式中：rij表示原始变量Xi与Xj的相关系数，取值范围为（1，p），其计算公式为：

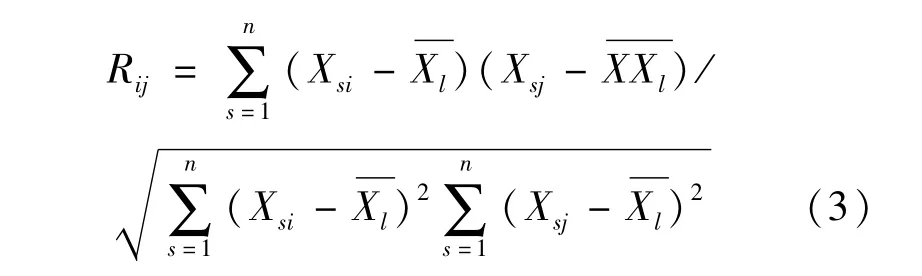
步骤3计算特征值和特征向量。求解特征方程|R-λIp|，求出特征值λi（i=1，2，…，P），并按大小顺序，即λ1≥λ2≥…≥λi≥0，分别求出特征值λi对应的特征向量ei（i=1，2，…，P）。

计算主成分贡献率和累加贡献。一般取累计贡献率达到80%以上的特征值λ1，…，λm（m≤p）分别对应第1，2，…，m个主成分。

主成分贡献率：

累加贡献率：

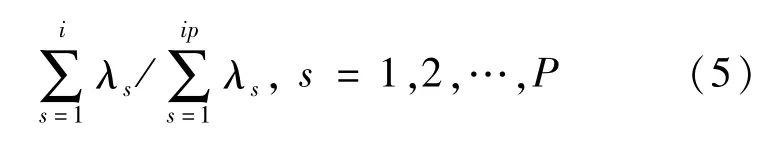
步骤4由主成分载荷计算得分。计算主成分荷载，以方差贡献率作为权重，通过对m个主成分进行加权求和计算得分，抽取主成分。

1.1.2 BP神经网络

BP（back propagation）神经网络属于人工神经网络的一种，由Rumelhart和McClelland等科学家于1986年提出。该神经网络是一种多层前馈神经网络，它通过对大脑神经系统功能和结构的模仿，基于学习信号正向传播和误差逆向传播机制进行训练，能实现复杂非线性映射功能。

图1表示经典3层BP神经网络的结构：由最基本的输入层、隐含层以及输出成组成。最初的学习信息从输入层输入，经由隐含层学习传播，最后由输出层输出并与期望值进行对比。如果不符合期望，误差作为调整信号，再由输出层→隐含层→输入层反方向传播，按照每层之间不同的连接权值加载误差，对各连接权值进行动态调整、反复学习，不断优化。BP神经网络的一大特点是可以根据不同的案例进行学习和训练，满足不同类型的审计工作需求。

图1 3层BP神经网络示意图

1.2 模型构建思路

构建PCA-BP审计风险识别模型的整体思路为：①构建影响审计风险的财务和非财务指标体系，对样本数据进行筛选和预处理。②运用PCA进行指标精简和优化，获取最终输入变量。③构建BP神经网络，以输入数据为基础进行训练，得到审计风险识别模型。④输入测试样本集验证模型准确率。模型构建流程见图2。

图2 PCA-BP模型构建流程框图

1.3 指标体系和样本选取

1.3.1 指标体系构建

指标体系的构建需要全面反映影响审计风险（包括重大错报风险和检查风险）的关键要素。舞弊三角理论指出，上市公司自身经营压力和证券市场对于公司的业绩压力使管理层进行财务报表错报，而公司治理水平和内部控制制度的不足，给管理层进行财务报表错报的机会和合理化借口。公司的经营状况可以通过偿债能力、发展能力等财务指标进行体现，股权集中指标、内部控制缺陷等非财务指标代表公司的治理水平和内部控制状况。

综合以上分析，选取了27个财务和非财务指标对重大错报风险和检查风险进行解释，参考李明辉等［21-22］的研究，选取审计费用存货占资产比例等6个指标来间接衡量审计风险水平。最终形成包括33个指标的审计风险识别指标体系，具体如表1所示。

表1 评价指标

1.3.2 样本选取

我国《中国注册会计师审计准则》中对于审计风险的定义为：财务报表存在重大错报而注册会计师发表不恰当审计意见的可能性。基于这一定义，选取被证监会处罚且审计意见为标准无保留和无保留意见的上市公司作为高审计风险水平样本公司。处罚条件包括：虚构利润；虚假记载；虚列资产；重大遗漏。其中，被证监会处罚的公司作为高审计风险样本（样本1），并选取相同数量上市公司为对照样本（样本0）。

以2009—2018年作为样本区间，从国泰安（CSMAR）数据库中筛选我国A股上市公司数据，样本筛选条件为：①1∶1选取同行业的配对公司样本。②根据2012年证监会分类标准进行行业匹配，剔除金融业公司。③配对公司的总体规模、效益等方面与高审计风险水平公司相当。④样本公司皆在A股证券市场交易。

剔除缺失数据之后，共选取了124家公司作为研究样本，取得1 195条数据记录，其中62个高审计风险样本1，62个低审计风险样本0。

2 实证分析

2.1 PCA指标处理

由于选用的审计风险评价指标多达33个，可能会带来重复信息，造成信息冗余和神经网络进行训练过度拟合，因此需要利用PCA方法实现数据精简，降低学习复杂度。本文中使用SPSS21软件进行PCA分析。

2.1.1 相关性检验

在PCA分析前，需要进行KMO和Bartlett的检验，该检验通过分析数据矩阵中各变量间的相关性，判断所采用的数据是否适合进行PCA分析。一般要求KMO大于0.5且Sig值小于0.05。表2显示了KMO和Bartlett检验结果，KMO值为0.653，大于0.5，且Sig值为0，小于0.05，说明样本数据具有较强相关性，存在数据冗余，可以利用PCA方法进行降维处理，进而降低神经网络的数据处理量，能有效提高模型的运行效率。

表2 KMO和Bartlett的检验结果

2.1.2 主成分提取

在KMO和Bartlett的检验后，将数据输入到SPSS21进行PCA分析。通过PCA降维处理，可以分析主成分对于原始指标信息的综合程度。PCA分析所得的方差贡献率反应单个主成分的综合能力，能力数值越大，综合原始数据能力也就越强。

通过PCA方法，提取出7个特征值大于1的主成分（见表3），这7个主成分的累计方差贡献率有87.661%，保留了大部分原始指标信息的基础上，可以作为神经网络的数据输入。

表3 主成分分析表

2.1.3 主成分得分及意义分析

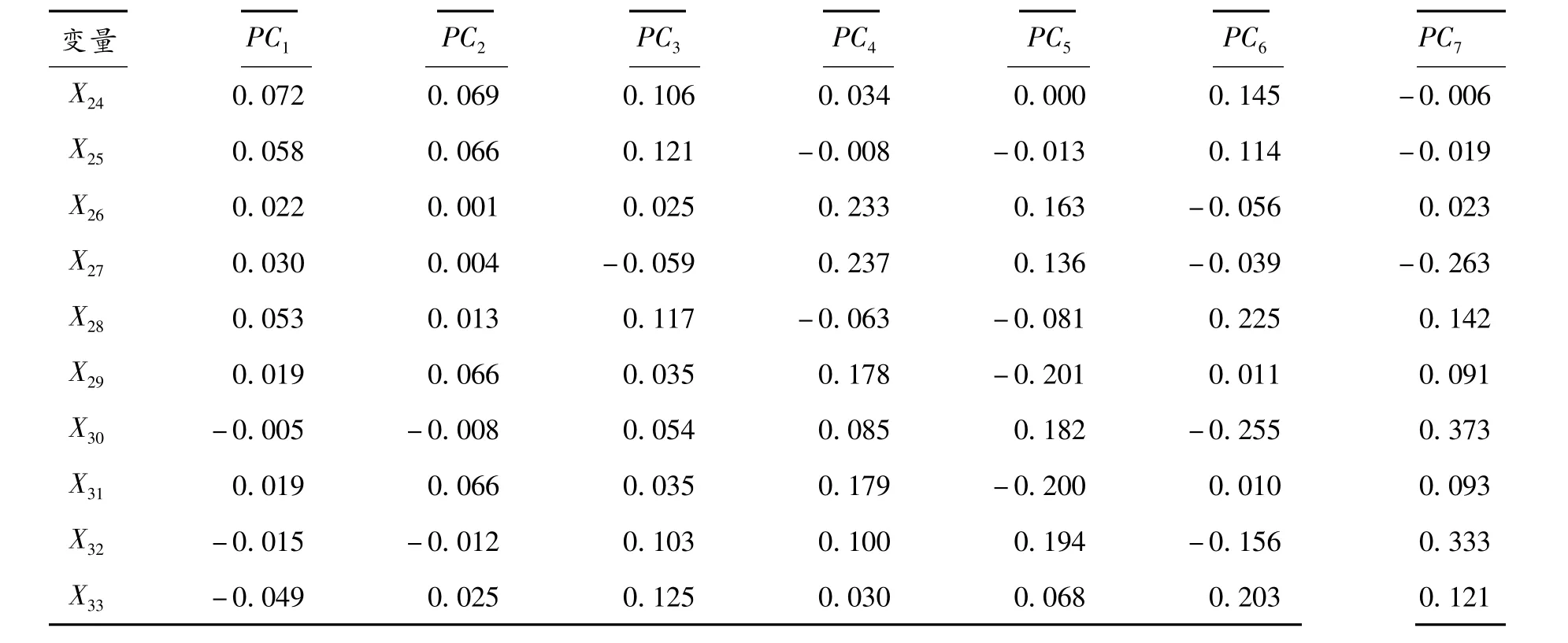
在提取出7个主成分后，输出主成分得分系数矩阵（表4），该矩阵将每个主成分分解为33个原始变量之间的线性组合，主成分PCi=得分系数X变量Xj（i=1，2，…，7；j=1，2，…，33）。系数矩阵显示主成分与各变量之间的相关性，可以分析每个主成分侧重反映的指标情况。

结合表3、4可知，在提取的7个主成分中，PC1和PC2累计方差贡献率达43.27%，这2个主成分综合反映企业整体的审计风险。

PC3主要与X15、X33正相关，X24显示应收账款周转率高低，X32反映经营杠杆水平，因而该主成分着重反映企业经营能力方面。

表4 主成分得分系数矩阵中的元素

续表（表4）

PC4主要与X29、X31正相关，X29说明前十大股东是否存在关联，X31说明企业是否存在内部控制缺陷，PC4侧重反映企业公司治理水平。

PC5主要与X11、X13正相关，分别代表企业的总资产增长率和营业收入增长率，反映企业发展能力。

PC6主要与X24、X25正相关，2项指标代表总资产净利润率（ROA）和净资产收益率，表明该主成分主要综合企业盈利能力信息。

PC7主要与X1、X3正相关，X1代表企业审计费用，X3代表企业存货占比，解释传统审计风险水平。

2.2 模型设置

根据已经筛选的主成分，输入到BP神经网络中，并按照图3的流程对BP神经网络进行设置，具体内容如下：

1）样本数据预处理。因为不同数据指标取值范围和表示方法存在差异，需要在神经网络学习之前进行预处理，将样本数据的格式和范围统一。采用一种快速的线性转换归一化算法对指标进行处理：

该算法中，x，y∈Rn。通过本算法，所有的数据都归一化到［0，1］范围。在Matlab中使用Mapminmax函数对数据集进行归一化处理。

2）数据分组。收集的1 195条数据分类为2组：训练集和测试集，每组数据中样本1和样本0数量比例为1∶1。其中：训练集数据797条，占样本总体比例67%，保证识别模型的识别学习能力；测试集数据398条，占样本总体比例33%，用于模型训练后进行准确性评价。

3）隐含层节点数确定。隐含层的节点数量决定数据训练的准确性和速度，如果选择的隐含层节点数过少，就会产生训练结果无法达到预期的精度目标的情况，如果选择的隐含层节点数过多，会出现训练时长延长和过度拟合的不良状况。隐含层数参考经验公式：

其中n1、n2、m、a分别代表输入层节点数、隐含层节点数、输出层节点。本文设置输入层节点数为10，隐含层节点为10，输出层节点为1。

4）函数与训练参数确定。选用的隐含层传递函数tansig函数、输出层传递函数purelin函数、模型学习函数learngdm函数以及模型训练函数trainlm函数。设置训练次数1 000，学习速率0.1，神经网络误差范围0.000 1。

5）训练集训练完成，利用学习后的神经网络模型对测试集进行识别，通过计算正确与错误识别数量，分析训练模型准确率。

6）分析数据结果，对模型进行评价。针对输出的结果数据与期望值进行对比，分析其误差，不断对模型进行调整，以达到最佳识别率。

2.3 结果分析

PCA-BP神经网络模型运行环境为Matlab R2019a。在设置好相关参数后，输入训练集对模型进行训练，并输入测试集进行测试。测试结果如图3、4所示，本次测试集识别准确率为89.44%，效果优秀。

图3 训练结果

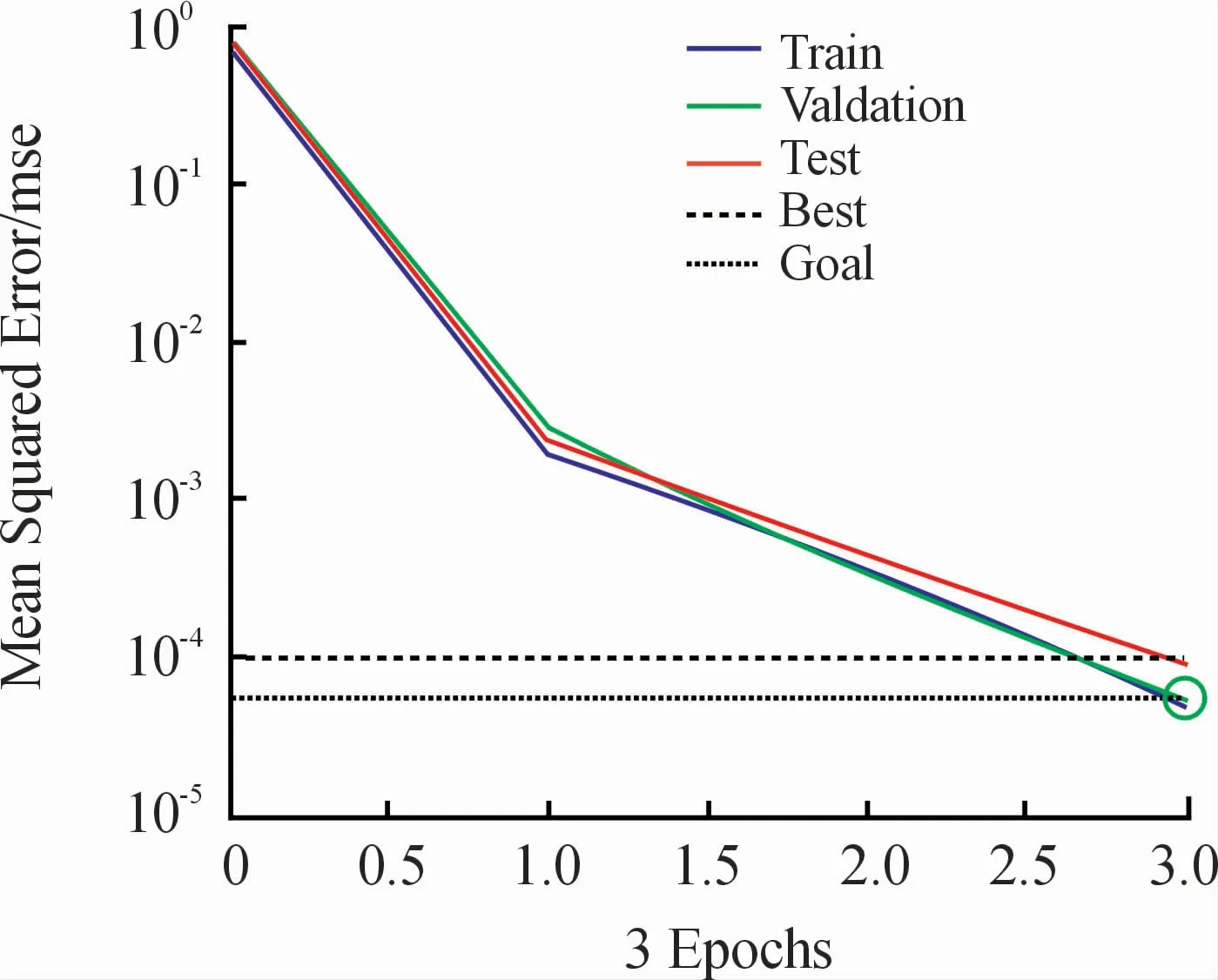
图4 误差下降曲线图

首先，针对模型识别情况，使用混淆矩阵进行评价。混淆矩阵又被称为误差矩阵，通过将预测类别和真实类别分别列示在矩阵的列和行上，对评价对象的精度进行分析。表5混淆矩阵显示2分类模式下PCA-BP审计风险识别模型输出的预测值和实际值的情况，可以计算出模型的整体正确率=（544+532）/1 195=90.04%，准确率较高。表6显示了混淆矩阵下的6类评价指标，可以看到正确率、精确率、灵敏度和特异度达到90%左右的水平，表明模型性能优秀。同时，假阴性率在研究中意味着高风险的样本被识别分类为低风险的样本，这会使得审计人员对审计风险的防范应对不当，从而发表错误审计意见，导致审计失败，造成严重后果。表中显示假阴性率有10.82%，说明PCA-BP神经网络模型下此类事件发生概率较低，有良好的预防效果。

表5 审计风险识别结果混淆矩阵

表6 模型评价

随后，统计识别准确率，具体结果如表7所示，在经过BP神经网络学习之后：①797个训练集样本中，有65个样本识别错误，准确率为91.84%。②1 195个整体样本中，有119个样本识别错误，准确率为90.04%。③398个测试集样本中，有42个样本识别错误，准确率为89.44%。训练集、样本整体、测试集三者识别准确率呈现下降趋势。训练集的预测准确率高，是因为整个审计风险识别模型以训练集为基础进行训练学习，经过神经网络模型的学习之后再次识别训练集，获得较高的识别准确率符合机器学习客观规律。学习后的识别模型去识别测试集时，虽然对比训练集数据准确率下降2.4个百分点，但依然拥有89.44%的准确率，这说明所构建的审计风险识别模型在面对陌生数据信息时，有89.44%的判断正确率，体现了模型优秀的识别能力。

表7 审计风险识别模型识别结果

最后，将模型与传统BP神经网络进行对比。在模型最大训练次数、训练精度、学习速率等参数不变的前提下，分别对传统BP神经网络和PCABP神经网络模型进行10次测试，统计2种模型的准确率、平均训练时间、平均迭代次数以及平均样本均方误差，整理得表8。

在表8中，PCA-BP神经网络模型平均准确率为90.54%，大于BP神经网络84.82%的准确率，展现出良好的鲁棒性。在模型的平均均方误差表现上，2个模型都达到10-4的精度要求，但PCABP神经网络平均均方误差对比传统BP神经网络有较大幅度下降。同时在平均训练时间和迭代次数上，PCA-BP神经网络模型也是优于BP神经网络。