时间平均莫尔条纹的信息隐藏技术

2021-06-10刘泽宇易军凯张阳平

重庆理工大学学报(自然科学) 2021年5期

刘泽宇，易军凯，张阳平

（1.北京信息科技大学自动化学院，北京 100192；2.北京化工大学信息科学与技术学院，北京 100029）

信息隐藏是把秘密的信息（如个人财产信息、网上银行等）通过各种隐蔽性处理，起到保护信息的作用。

莫尔效应作为一种光学效应，在2片光栅以不同的角度、不同的频率、不同的方向相交时形成各种各样的图案，以达到图案多变的目的。基于莫尔效应的以上特征，提出了基于莫尔条纹的信息隐藏技术，因为该技术隐蔽性较低，本文提出基于时间平均莫尔条纹的概念。在加密过程中，嵌入秘密信息可以利用随机相位编码和相位匹配算法的方法进行加密；解密过程中，使用时间平均条纹振动来产生干涉效果。图片以特定的方向和振幅振动时，才会显现秘密信息。

1 莫尔效应及其应用

1.1 莫尔效应介绍

莫尔效应［1］又称光栅效应。莫尔效应是典型的光学现象，是利用2个平面的光栅［2］互相干涉形成的。肉眼识别能力有限，在干涉部分难以快速识别点、直线、曲线，使得干涉区域形成看似图案的视觉效果，当两光栅干涉角度、方向和自身频率不同时，出现的图案也不相同。

1.2 莫尔条纹介绍

光衍射和干涉形成的视觉效果产生莫尔条纹，形成阴影区域和反光区域，出现的暗部和亮部交织的条纹，称为莫尔条纹，见图1。

图1 莫尔条纹图像

这里提出莫尔条纹周期的概念，莫尔条纹周期的函数为：

式中：t1表示母版光栅的周期；t2在函数中代表检测光栅的周期；θ表示两光栅之间的夹角。特别地，当t1和t2相等时，即t1=t2=t，莫尔条纹的周期函数为：

由式（2）可知，当夹角θ越小时，莫尔周期也会因此越大，同时莫尔效应表现现象就会越明显。

1.3 莫尔效应的应用

莫尔效应在工业和印刷方面都有广泛的应用。其中在工业方面应用主要包括角度［3］、相位、等精密测量、形变检测、轨迹控制、三维形貌检测等。文献［4］提出了一种高速光栅光纤传感器，它支持在极端环境（如燃烧、爆炸）中测量能量物质的速度、位置、温度和压力。在印刷领域，莫尔效应用于印刷防伪［5］。通常，半色调图像［6］是指经过特殊操作后出现的打印图像中，用离散点的面积大小或密度来表示颜色的变化。由于目前打印机等输出设备的颜色不能满足原始图像的需要，必须对图像数据进行取整量化，使其达到输出设备对相应的颜色性能要求，这个过程称为加网［7］。因为灰度值不同，半色调图像网点的大小（调幅加网）或者密度（调频加网）［8］会有一些不同，采用调幅加网或者调频加网的方法，将色彩逐级变化的连续色调图像转换为离散网点表示的半色调图像。半色调图像定义为排列具有规律性变化的网点而成的图像，在实验中修改秘密信息区域的半色调图像中网点的属性，如位置、密度、排列方向等，这样会与未更改的其他网点形成区别，输出后可以实现信息隐藏［9］和防伪印刷的目的。

2 信息隐藏技术

2.1 人眼视觉系统

人的肉眼可看成人眼视觉系统，又称HVS［10］。人眼视觉系统是一个天然的可处理外部图像信息的系统，但它却又不是完美的，如视觉惰性、低通性、掩蔽性。

2.2 可视密码

可视密码［11］首次被Naor和Shamir提出，利用了密码分享的途径，可以用人的肉眼辨识，不需要复杂的计算机和密码学计算。是把密码分为多个子密码n，只有当k个子密码组合时，才能恢复密码。子密码数低于k时，计算无法解密。这可以避免巨大的计算量，通过肉眼观察出密码。

3 平均莫尔条纹信息隐藏过程

按照形状各异的栅格，用不同办法把信息加密隐藏在母板上，分为以下2类：

直线光栅应用于信息隐藏。将光栅模板重叠在母版图像上，如果栅格与隐藏信息重叠，那么把该光栅点向非光栅方向移动。为了避免隐藏信息的缺失，用光栅的偏移点交换母版偏移点的方法来进行改进。

曲线光栅应用于信息隐藏。栅格之间会有一定角度，当栅格点移动时，可能把隐藏信息的栅格点移动到没有信息的栅格点上，使信息消失。另外，可能使有信息的栅格点移动，与其他栅格点连接，会使信息模糊，容易在识别过程中出现错误。因此按照直线光栅的办法，只对边缘相交的光栅点进行移动，并对移动位置进行检测。具体方法为：一是当旁边没有干扰的栅格点，就根据直线栅格规则移动；二是如果旁边有栅格点，再看旁边的栅格点有没有信息，若没有则移动该栅格点，同样也移动周围栅格点，如果旁边栅格点里有信息，再看该隐藏信息中有没有关键信息，可以归归纳为：

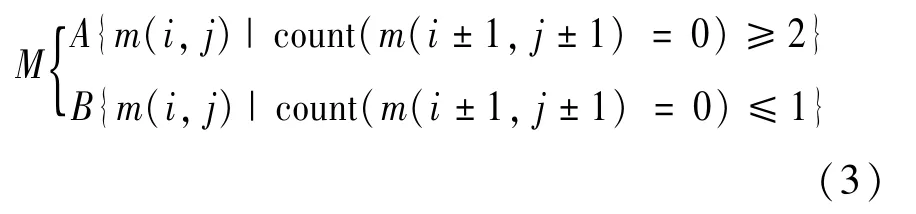
式中：A表示旁边栅格点无关键信息的集合；B表示旁边栅格有关键信息的集合。

几何莫尔技术是基于2个常规光栅叠加产生相干条纹的视觉分析，是一种经典的平面非破坏性光学实验技术。关于莫尔效应研究的现状分为莫尔条纹的分布和如何产生特定的莫尔条纹等2个方向。这涉及2种图像的生成，当这2幅图重叠时，即可看见非常清晰的莫尔条纹（描述了光栅形变区域的形变量）。为了将莫尔效应用算法表示出来，用一组黑白两色周期性变化的栅格来表示光栅，当光栅趋于平衡状态时，视为一个一维谐波函数［12］，即：

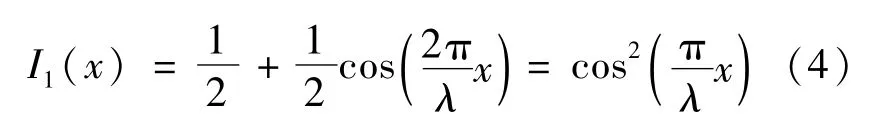
式中：λ表示栅距；函数I1（x）的值表示光栅表面x点的灰度值。

当有变化出现在莫尔光栅x点处时，用f（x）表示，函数I2（x）可以表示为：

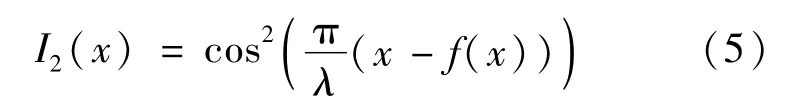
将I1与相叠加，产生的图像表示为Id，则Id可以表示为：

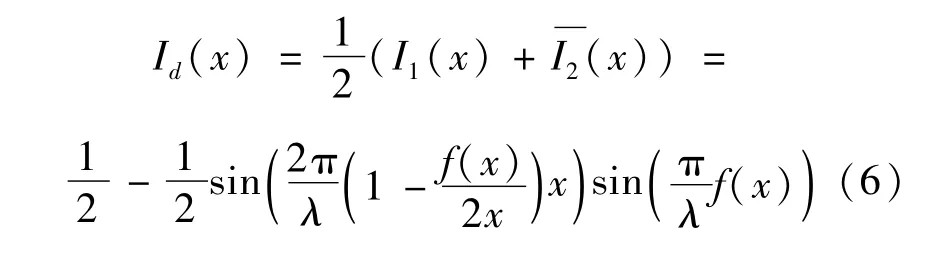
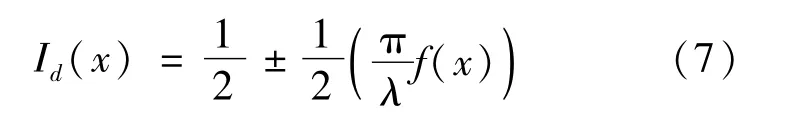
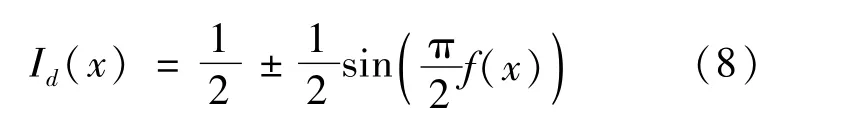
莫尔效应的加密解密原理如图2所示，图2（a）表示莫尔光栅的波形图，栅距λ=0.8；图2（b）表示需要加密的函数波形，即形变函数f（x）；图2（c）表示I2的波形光栅经过f（x）形变后的波形图，c=0.4；图2（d）表示函数的包络波形图。Id波形图的包络与原始形变函数基本一致，计算Id+I1即可获得原始图像的包络，再经过低通滤波，即可获取到原始图像。

图2 莫尔效应的加密解密原理

时间平均莫尔条纹图像信息隐藏技术只生成一幅图像，编码生成的图像看起来像一副随机混乱的图像。秘密图像只有按照预先计算的振幅振动才能显示原始的秘密信息。

光栅图层在x点处的灰度值F（x）由式（4）确定，图层根据谐波振动，振动函数计算公式为：

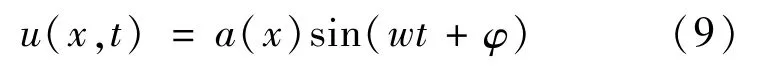
式中：t是时间，代表x点谐波振幅；w代表角速度；φ代表初始相位。因此，振动过程中x点灰度值FT（x，y）计算公式为：

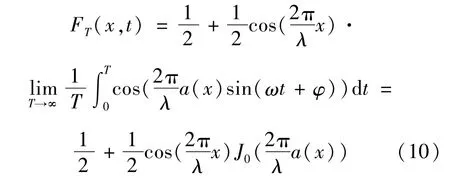
式中：T是曝光时间；J0是第一类0阶贝塞尔函数［13］。在符合的位置上，将会出现时间平均莫尔条纹，从中得到振幅函数和栅距函数为：

式中：ri是第一类0阶贝塞尔函数的i号根；ai是第i个条纹振幅。

根据式（9）可知，振动频率与时间平均条纹无关。图3表示时间平均条纹的计算构建过程，取栅距λ=0.2，除栅格区，其余部分是白色。假设a（x）=x，当左侧的部分出现清楚的光栅条纹时，x点的振幅值等于坐标值，随着谐波振幅的增大，光栅条纹也会变得模糊，灰度值达到稳定值的一半时，会出现周期的灰度条纹，还不能生成时间平均莫尔条纹。即使振幅逐渐增加或减少，图像对比度的变化也不单调，由第一类0阶贝塞尔函数，根据式（11）计算得出。在满足式（11）的区域周围可以构成时间平均条纹，振动频率与时间平均莫尔条纹无关。为了保证较好的条纹效果，需要足够长的曝光时间。

图3 时间平均莫尔条纹的形成原理

时间平均莫尔条纹出现在0阶贝塞尔函数根区域周围，其他部分未出现。

当振幅a是一个常数时，计算（x，y）点灰度值无需根据式（9）对时间进行无限积分，只需求多次振动灰度值的积分和，如式（12）所示。在实际操作中这意味着通过计算多次振动的灰度值的平均数，来最终确定（x，y）点的灰度。通过式（12）计算原来的静态图像，生成每次振动的灰度值的形变程度。

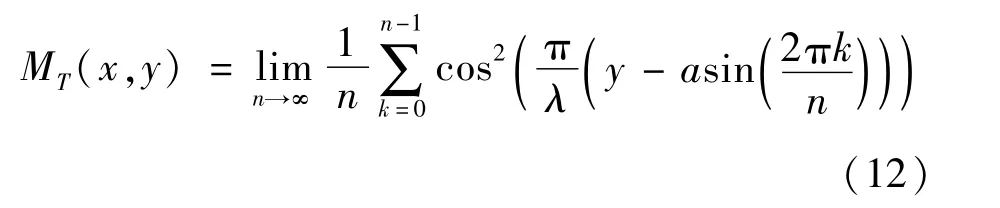
取n=256，得到前32个精确的时间平均莫尔条纹，前3条实现数字区域的可视化。固定振幅的时间平均图像如图4所示，对莫尔条纹进行不同振幅的振动可得时间平均莫尔条纹。

图4展示了时间平均条纹的形成过程，整幅图像选取的振幅都是常数，图4（a）五角星表示原来图像，由一组光栅组成，此时光栅之间的距离为0.3，图4（b）是将图4（a）按照振幅为0.05振动得到的图像，图4（c）是用图4（a）按照振幅为0.1振动得到的图像，图4（d）是用图4（a）按照振幅为0.15振动得到的图像。

图4 固定振幅的时间平均图像

图4 （a）所在部分并不会产生干涉条纹，产生了些模糊。图4（c）、图4（d）进行振动出现了平均莫尔条纹。原图像（图4（a））信息隐藏的结果用肉眼识别，明显存在安全隐患，需要通过额外的转换来保证成为安全的信息载体，保证振动转换之后的图像，秘密信息所在区域必须形成干涉条纹，实现秘密信息的显现。

使用相位匹配［14］算法和随机相位偏差来加工背景图像，使秘密信息更难显现，相位匹配算法的作用是使秘密信息和背景图像的连贯性更好。为了使原始图像有更多干扰，更难识别，增加了随机相位算法。以上两算法的加入，都不会影响时间平均条纹的形成，因此可以通过振动来获取解密效果。

图5表示贝塞尔函数根、振幅与栅距的关系，纵坐标为振幅，横坐标为栅距，同一坐标的点对应同一振幅。

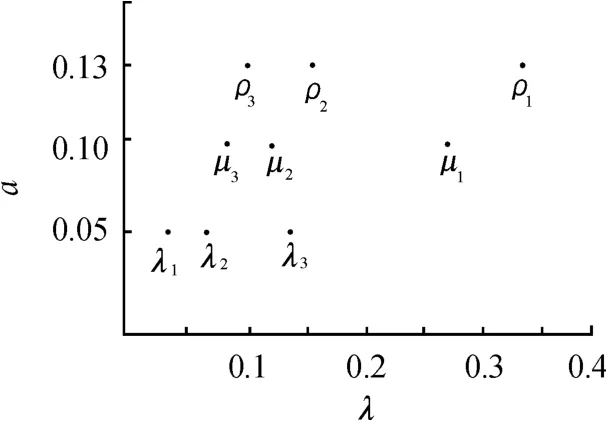
图5 不同振幅对应的栅距

多重隐藏方法如图6所示，将一个矩形的图像分成25个不同的区域，如图6（a）所示，各个部分都是通过指定栅距的莫尔条纹组成，要求这些莫尔条纹的方向相同，如图6（b）、图6（c）、图6（d）所示。

图6 多重隐藏方法

构建了3种非重叠模式的光栅，莫尔光栅的栅距是预先选定的，当以不同振幅进行振动时，不同模式的光栅将会可视化。根据式（11），计算出时间平均条纹对应的前3个栅距，在实际中，一个振幅可以对应更多的栅距。根据振幅a1计算出3个栅距，选择不同的振幅a1、a2、a3，计算得到不同的栅距，而且，每个栅格对应的栅距是随机排布的，如图6（a）所示。假设采用图6（c）中的光栅模式进行加密，将原始图像还原，需要进行初始随机相位震荡。不法分子必须知道需要振动图像才能显示出秘密信息，这样的振动需要特殊设备的辅助，通过多次实验很可能无法解密出秘密信息。以振幅a1振动时，图6（b）中光栅模式将可视化；以振幅a2振动时，图6（c）中的光栅模式将可视化；以振幅a3振动时，图6（d）中的光栅模式将可视化，不法分子无法确定是秘密信息究竟对应于哪一个模式。

4 实验与分析

取谐波震荡函数的频率ω=100 Hz，曝光时间T=1 s，因此在曝光时间内，出现了100次振动，选第一类0阶贝塞尔函数的第一个根，由式（12）得到背景区域形成时间平均莫尔条纹所需要的振幅a0=0.057 4，则谐波振动的函数为μ（x，t）=0.057 4sin（100t+φ）。

以不同振幅振动载秘图像产生的时间平均图像如图7所示，对产生的时间平均图像进行对比度增强，能够更加明显地展示隐藏信息重现的效果。将载秘图像按照振幅a=0.057 4振动产生的解密效果，可以看出只有背景区域由于干涉形成了一定模糊效果的灰度图像，如图7（d）所示。秘密光栅区域由于不符合振幅要求，虽然产生了一定的波纹扰动，但是没有形成灰度模糊效果，仍然以随机条纹的形式存在。实际上背景区域以及秘密图像区域均由栅线组成，在本质上并无差别，因此也可以以秘密区域形成时间平均莫尔条纹所需的振幅a=0.074 7振动，得到反色的秘密图案。但是如果随机选择振幅，则无法产生相应的灰度图像。

图7 时间平均图像

在实际的解密过程中，需要严格控制振动的频率、方向以及振幅，才可以形成时间平均莫尔条纹。理想情况下，谐波振动的方向应该与光栅条纹的方向严格正交，才可以产生最好的时间平均效果；并且谐波振动的最小频率应该大于等于人眼视觉系统的最大截止频率，否则，会造成振动过程中干涉产生的时间平均莫尔条纹中断，无法形成灰度连续的区域，影响人眼识别。

现在有文本信息KAUNAS，要求把这个信息隐藏在背景光栅中，如图8所示。

图8 “KAUNAS”嵌入背景光栅

首先需要选取背景光栅的振幅，以备解密时需要。在实验中选取背景光栅的振幅a=0.057 4，因此可以计算出背景光栅的栅距，这个值可以保证在产生时间平均条纹时，背景光栅不会消失，即使是不同的栅距也有可能因为相同的振幅产生干涉条纹。其次选择秘密文本区域对应的栅距，第一类0阶贝塞尔函数有多个“KAUNAS”嵌入背景光栅。

图8为将秘密文本信息编码隐藏到背景莫尔光栅图像后的效果，其中背景莫尔光栅的栅距，秘密文本“KAUNAS”区域对应光栅的栅距。

简单的嵌入无法达到隐藏信息的要求，在图8基础上，先进行相位匹配操作，使得秘密文本区域与背景光栅区域实现平滑过渡，执行随机相位偏转操作，增加随机相位差，扫描检查秘密文本区域与背景光栅连接区域的边界，如果有较大相位差，则再次执行相位匹配操作，在最大程度上减少秘密文本区域与背景光栅的相位差，所得结果如图9所示。

图9 执行随机相位偏转之后的隐藏效果

在现实操作的过程中，显现重构被隐藏的秘密信息，在这里需要使用振动台来辅助，对载密图像以指定方法进行振动，因为肉眼视觉滞后的原因，看到时间平均莫尔条纹的形成，因此显现出原本的秘密信息。由于实验需要，在计算机上模拟了载密图像的振动效果，结果显现了被隐藏的秘密信息。

以不同振幅振动获取解密文本如图10所示，图10（a）为将载密图像依照a=0.057 4振动得到的结果，秘密文本被干涉出现了模糊不清的情况。因为振幅没有达到规定的标准，背景光栅上出现了移动的波纹扰动，未出现模糊的灰度区域，可以看到随机条纹。

图10 以不同振幅振动获取解密文本

背景区域及秘密文本区域很相似，以背景部分a=0.074 7振动，在背景区域形成灰度图像［15］，而秘密文本区域仍保持杂乱的随机波纹效果，如图10（b）所示。随机选择一个不满足式（5）中关系的振幅a=0.133 4，无法产生相应的灰度图像，如图10（c）所示。

在实际的解密过程中，需要严格控制振动的频率以及方向，谐波震荡的方向应该与时间莫尔条纹的方向严格垂直，并且振动的最小频率应该大于等于人眼视觉系统的最大截止频率，否则时间莫尔条纹干涉产生的视觉模糊效果存在间断。根据上文的结论，振动频率不影响时间平均条纹的产生，因此理论上可以不借助振动台，只依靠手振动来完成信息解密，但是在实践中，仅依靠手的控制无法精确控制振动的振幅以及方向，并且依靠手的振动频率无法达到人眼视觉系统的最大截止频率，因此实践中还是要借助振动台的辅助。

为了更加有效展示视觉解密的效果，截取图10（a）和图10（b）中字符“K”上边的部分进行放大，如图11（a）和图11（b）所示，可以明显地看到隐藏文本部分与背景图像部分有明显的边界。