非结构化环境下四足机器人避障性能研究

吴国洋

（攀枝花学院 钒钛学院，四川 攀枝花 617000）

为了提高机器人在非结构化环境下的平稳通过能力，使其更加贴近生物的自然运动，国内学者围绕结构优化设计和控制2个部分做出了一定的研究。通过结构设计层面来实现避障功能的文献较多，如肖时雨等［1］基于人体爬树运动研制的一种新型四壁式巡检机器人，王吉岱等［2］设计了一种具有越障效率高、爬坡能力强的四臂巡检机器人机械结构，房立金等［3］设计的通过关节匹配实现越障平衡的新型四臂巡检机器人，郭文增等［4］提出了一种兼具轮式和履带式高越障性的机器人，孟广耀等［5］提出了一种可变形新式履带机器人。另一方面，关于机器人避障控制方面的研究甚少，且只是在现有的结构上采用智能算法或神经网络进行控制，如杨志成等［6］提出了一种具有避障功能的控制系统，王云倩等［7］提出了一种具有探测障碍、位姿调整的CPG运动控制方法，李志海等［8］提出了一种双足机器人避障运动的控制系统，韩宝玲等［9］提出了一种基于新粒子群算法的四足机器人机身横向调整参数优化方法，葛卓等［10］提出了四足机器人坡面/避障运动数学模型。

本文结合生物界蜘蛛的运动特点，针对非结构化环境的复杂路面，研究一种多足机器人，结合空间机构学的数学基础，求解多足机器人的运动学模型，利用CPG神经网络对多足机器人构建运动拓扑结构，对其在平坦路面、圆柱障碍物等2种环境进行仿真试验，以验证结构仿生、功能仿生在机器人非结构化环境中的合理性与有效性。

1 多足机器人运动学模型

1.1 运动学数学基础

通常来讲，多足步行机器人主要包括机体与腿2个部分；其中，单腿由髋关节、膝关节和脚部3个部分组成，且通过髋关节铰接于机体。机器人行走过程中，与地面接触的腿称为站立腿，与地面非接触的腿称为摆动腿，站立腿在转变为摆动腿之前与地面的接触点假设保持不变。由此，多足机器人运动学模型由站立腿和摆动腿2个部分的位姿组成。下文将逐个对站立腿、摆动腿的运动学模型进行介绍与阐述。

1）站立腿的运动学模型

机器人站立腿的结构如图1所示，Ai表示站立腿的立足点；Bi表示机体臀关节的连接点；lj（j=1，2，…，5）表示第j个连杆的长度，l1、l2、l3为平面连杆；φi、φi、χi表示驱动关节的位置（或角度）；εi、δi、θi表示被动关节的位置；XYZ）表示固定坐标系；表示臀关节Bi上的相对坐标系，且满足其旋转轴线和z轴重合；为Ai，Bi在参考坐标系∑o中的位置矢量。脚关节模型由相互正交的旋转关节代替，且旋转关节分别为图中的θi、δi、εi及连杆l4、l5（通常，l4=l5=0）。

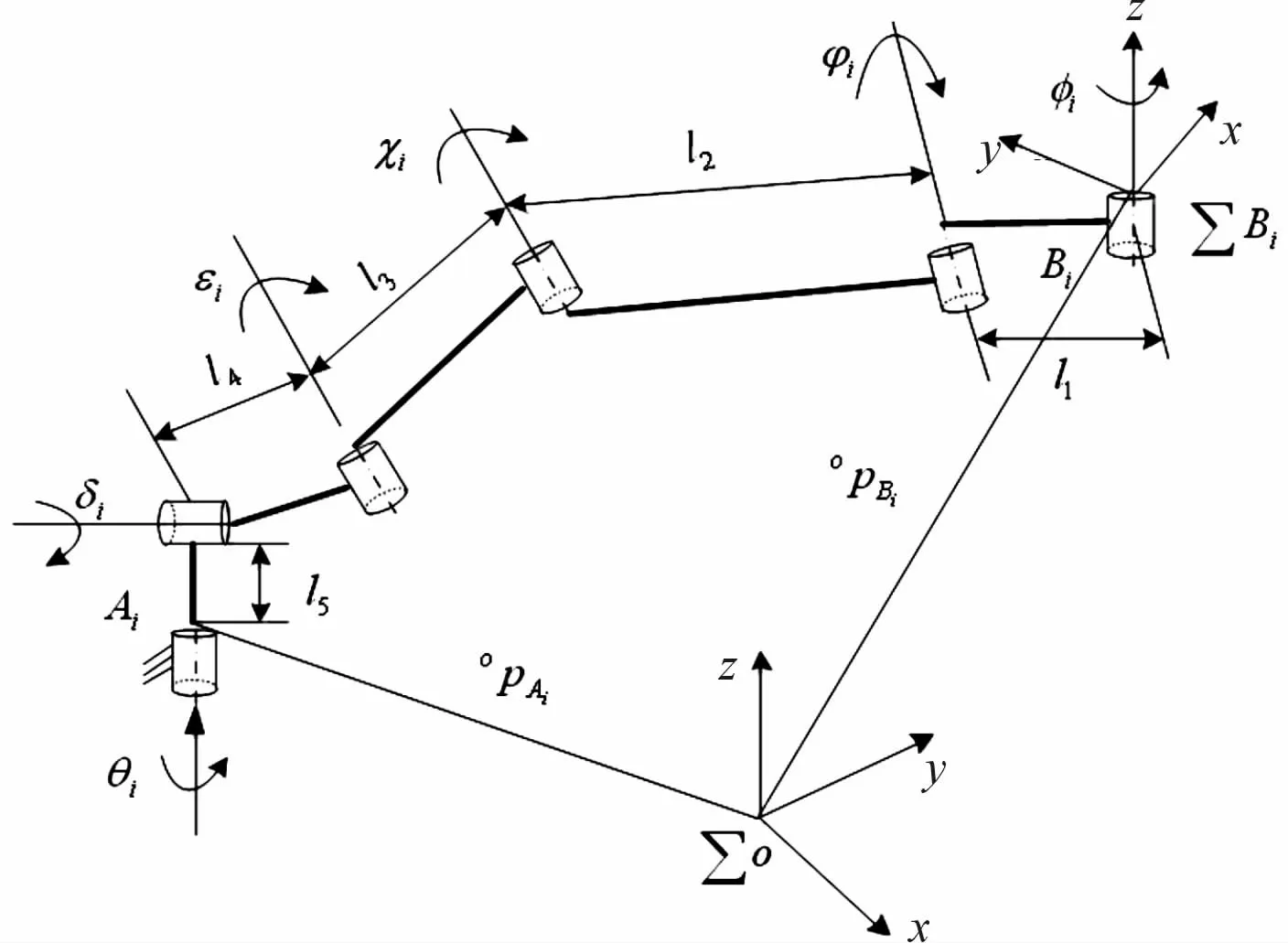
图1 多足机器人站立腿结构示意图

为描述机体、连杆和地面的几何关系采用齐次变换矩阵表示；其中，表示坐标系的原点位置和旋转矩阵，即：

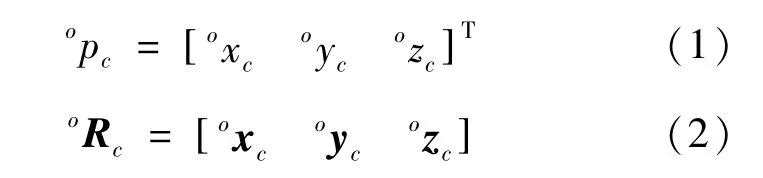
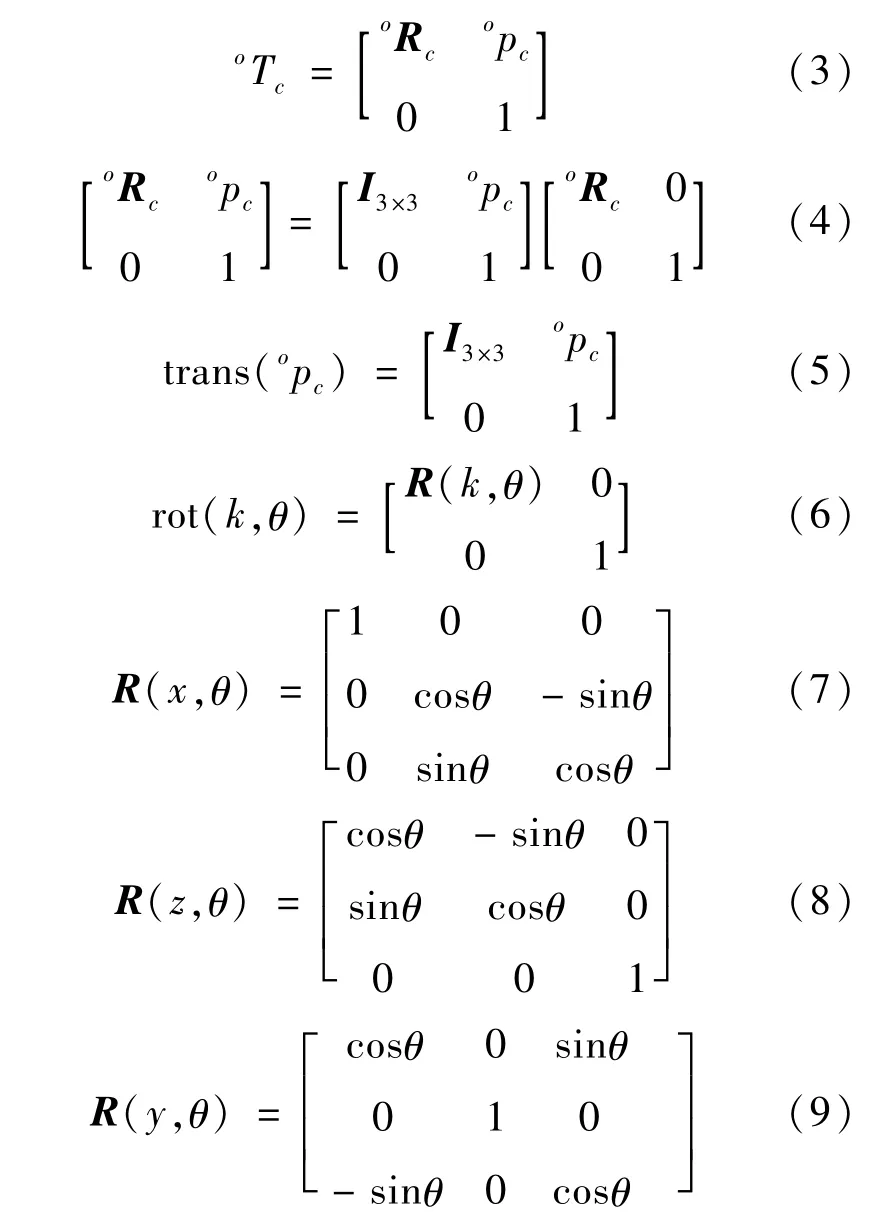
式中：I3×3为3阶单位矩阵。此处，trans（opc）、rot（k，θ）分别表示坐标系平移和旋转变换。R（k，θ）表示坐标系绕轴k旋转θ角度之后新坐标系的方位矩阵。

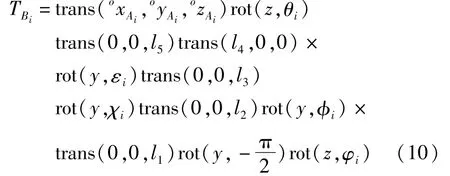
式中：（oxAi，oyAi，ozAi）为Ai在∑o的位置坐标，展开得：

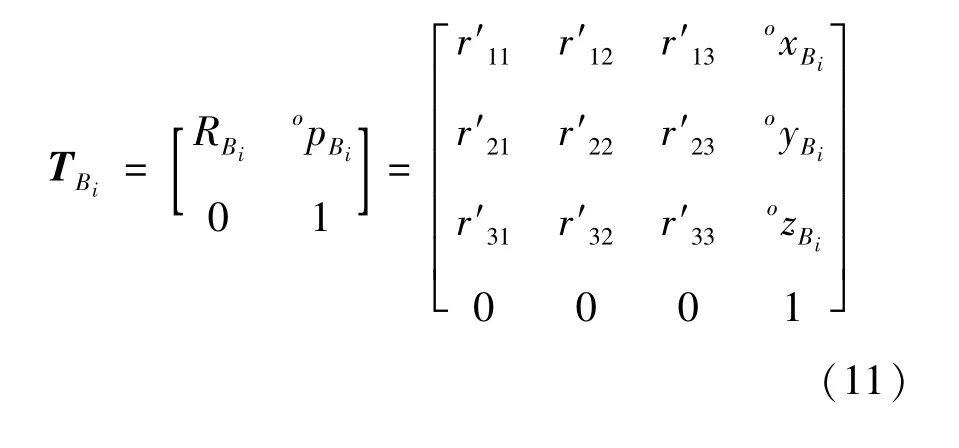
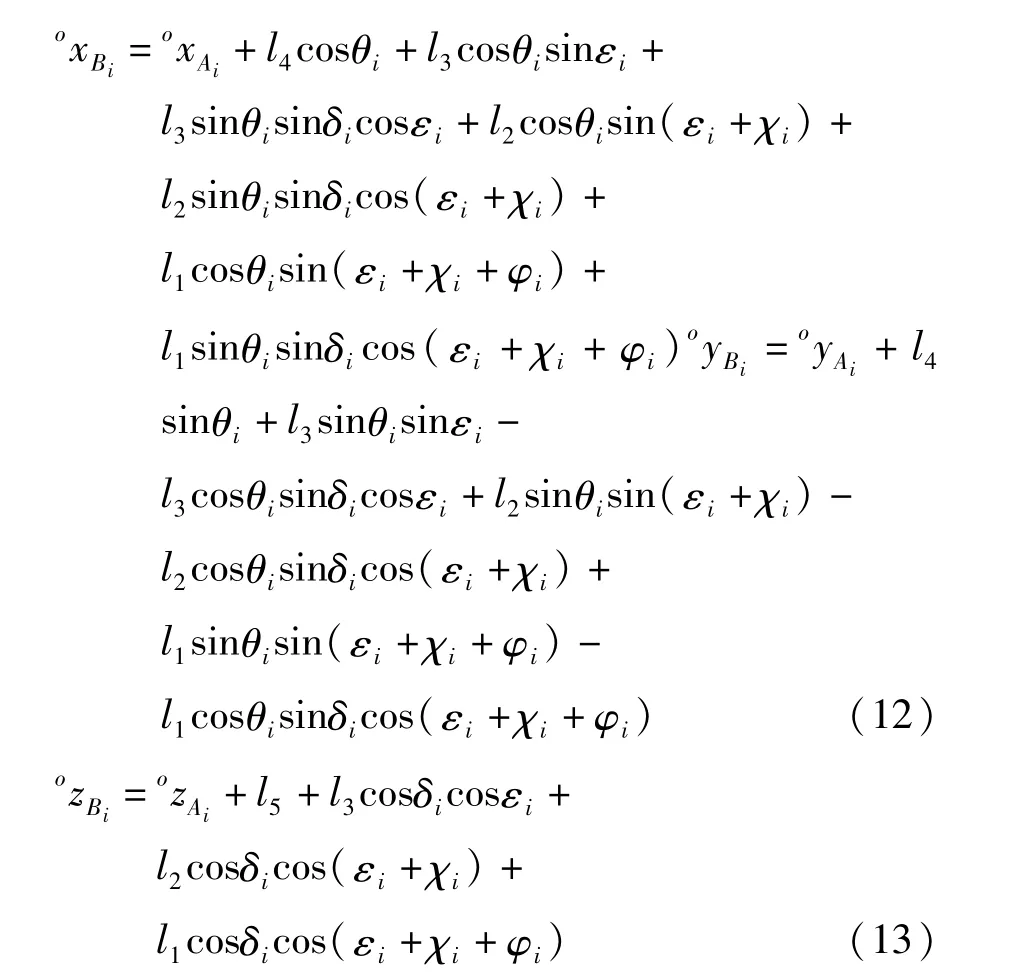
式中：θi、δi、εi表示连杆平面和接触地面之间的几何关系；φi表示的是连杆与机器人机体的方向关系；表示的是机体在坐标系中的位置。因此，为描述机器人位姿的站立腿运动学模型。

2）摆动腿的运动学模型

驱动关节摆动腿结构如图2所示。

由机器人空间机构运动学可知，多足机器人摆动腿的正运动学即依据机器人当前本体位姿和腿驱动关节变量来求解机器人的脚在的位置则有

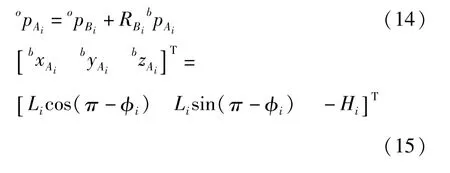
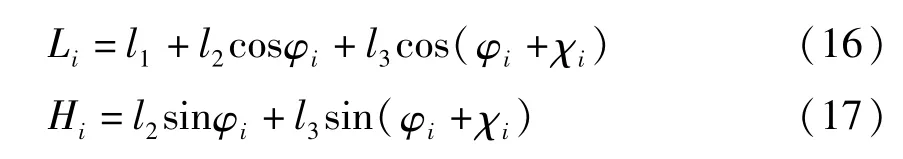
则Ai在的位置坐标：

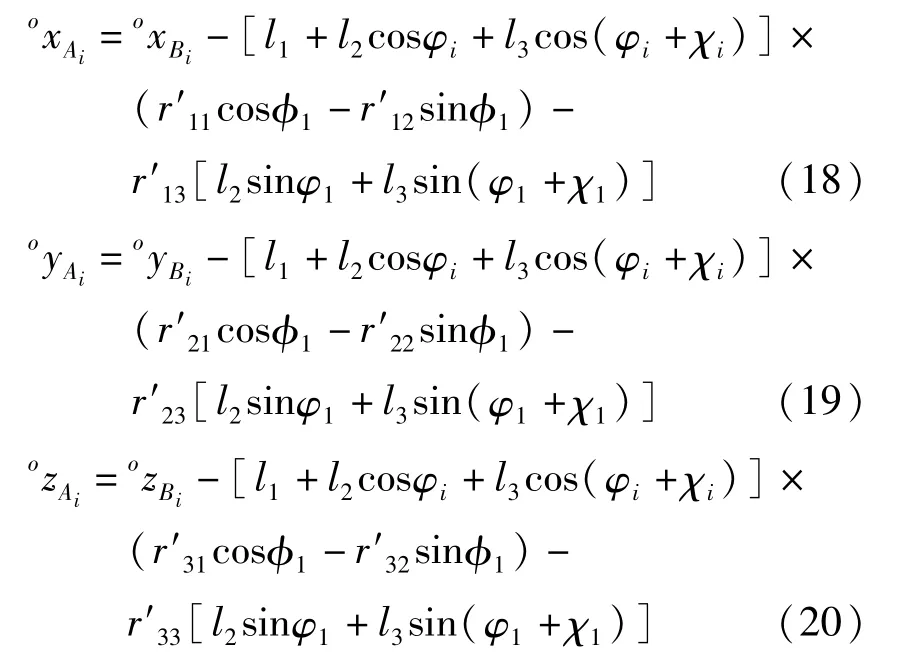
1.2 四足机器人运动学模型

自然界中，许多爬行动物的运动多数是通过提供动力的肌肉和驱动关节的配合来实现的。为了适应生存环境，动物的肢体在逐步进化，演变成与运动方式匹配的骨骼结构。当前，动物的肢体关节主要分为膝式和肘式2种类型，此处选取膝式结构对机器人的结构进行配置设计，如图3所示。

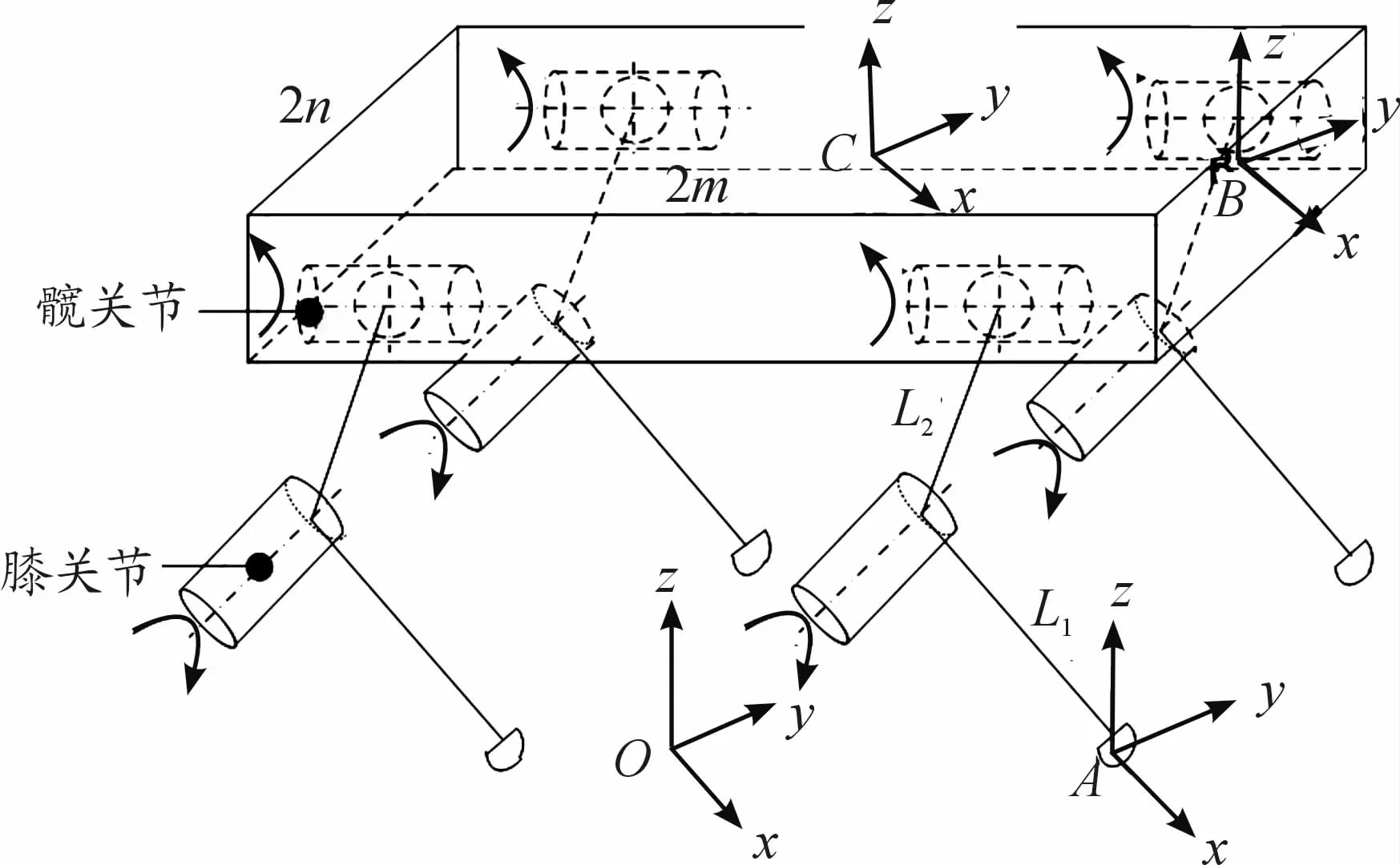
图3 四足机器人结构

由图3可知，该机器人结构由膝式关节组成，且每个膝关节包括髋关节与膝关节，自由度分别设置为2和1，此图中腿关节的脚环节采用简化处理（不含有自由度）。因此，该全膝式机器人的步行运动等同于具有3条站立腿、1条摆动腿的运动平台相对于地面的运动。分别表示机体坐标系、原点坐标系、单腿脚关节落脚点坐标系和单腿髋关节与机体连接处的坐标系，机体长宽分别为2m、2n。

将该机器人连杆平面投影到机体坐标系∑C中xy平面可得图4。

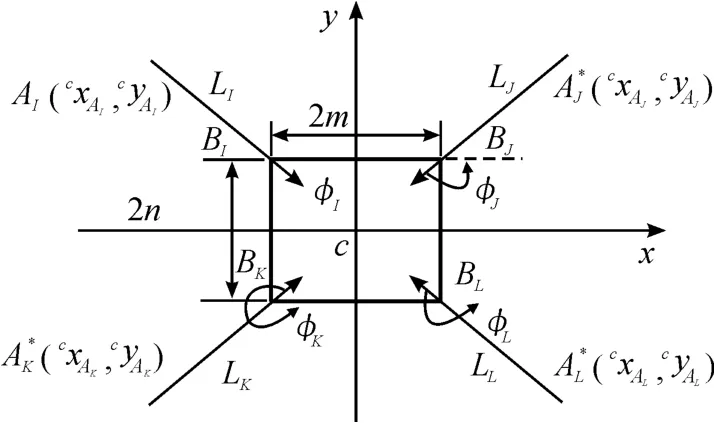
图4 四足机器人平面投影

在∑C中XY平面的投影

则有：

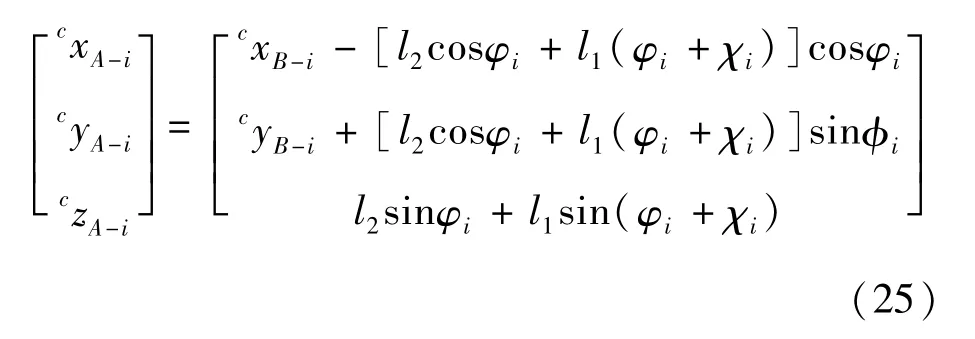
鉴于全膝式机器腿关节通过髋关节铰接于机体，则有：

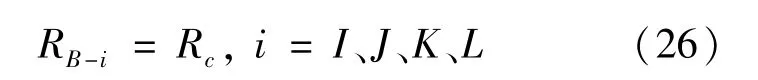
∑C相对于原点坐标系∑O的方向矩阵用Rc表示，RB同理；cpB-i为常数矢量，且为m、n的函数。

则由式（14）（25）（26）得全膝式机器人在原点坐标系∑O中的坐标（即运动学方程）：

2 基于CPG的机器人控制网络

动物运动控制结构由高层中枢、中枢模式发生器、效应器和外界环境等部分组成，如图5所示。当运动控制结构执行运动指令时，动物结合外界环境的实时条件，控制网络选取匹配的节律运动模式进行运动。在运动过程中，运动控制网络在外界反馈信息和本体感受器的基础上，自主调整运动模型及节律运动中的相关参数以实现动物在非结构化环境中的避障等功能。其中，CPG是产生节律运动、实现节律运动的中心控制单元，是组成具有多个震荡中心分布网络系统的单元，且其由多个中间神经元构成。该运动控制结构网络通过调节神经元之间的相互抑制以产生稳定的周期信号，进而实现躯体相关的节律运动。CPG中各神经元之间的突触连接可通过改变参数实现变化，因而具备多种输出行为，可用于实现动物的多种运动模式。

图5 动物的运动控制网络

2.1 单神经元网络结构

步态常用来表示足式动物各腿之间具有固定相位关系的行走模式［11-12］。由于动物自身的结构属性，其在不同运动状态下的步态还是存在差异的。步态根据各腿负载因子的大小，可分为规则步态和不规则步态，前者指的是各腿运动规律相同及相位差相同，相位差是机器人步态描述的关键参数。四足动物按照运动的节奏，一般分为单拍步态、双拍步态、准两拍步态和四拍步态［13］。

如上所述，机器人步态指的是在运动过程中每条腿依次按照预定的顺序进行运动的过程［14］。理想的步态生成与转换方法应当使机器人产生自然协调的步态，并能实现快速平稳的步态转换。当前，机器人产生稳定步态的模型主要有基于神经元的CPG模型和基于非线性振荡器的CPG模型2种形式。鉴于该全膝式机器人需要稳定的周期性振荡信号，并且易于实现，选取Hopf振荡器［15］作为CPG的单元模型，数学模型如下：

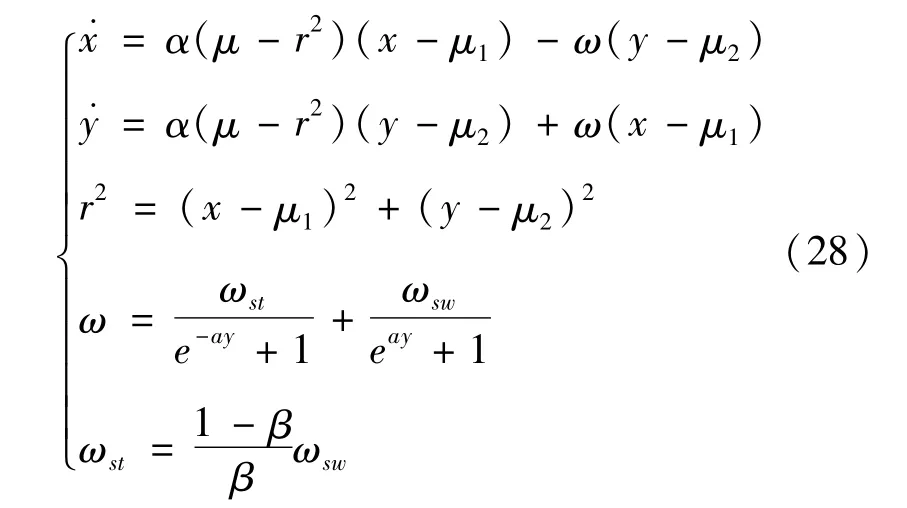
对该数学模型进行数字仿真，如图6所示，上述模型描述的振荡器可构建稳定的周期性信号。其中，x表示机器人的关节信号，具体来讲，一个步态周期内，上升段表示腿部的摆动相，下降段表示腿部的支撑相。

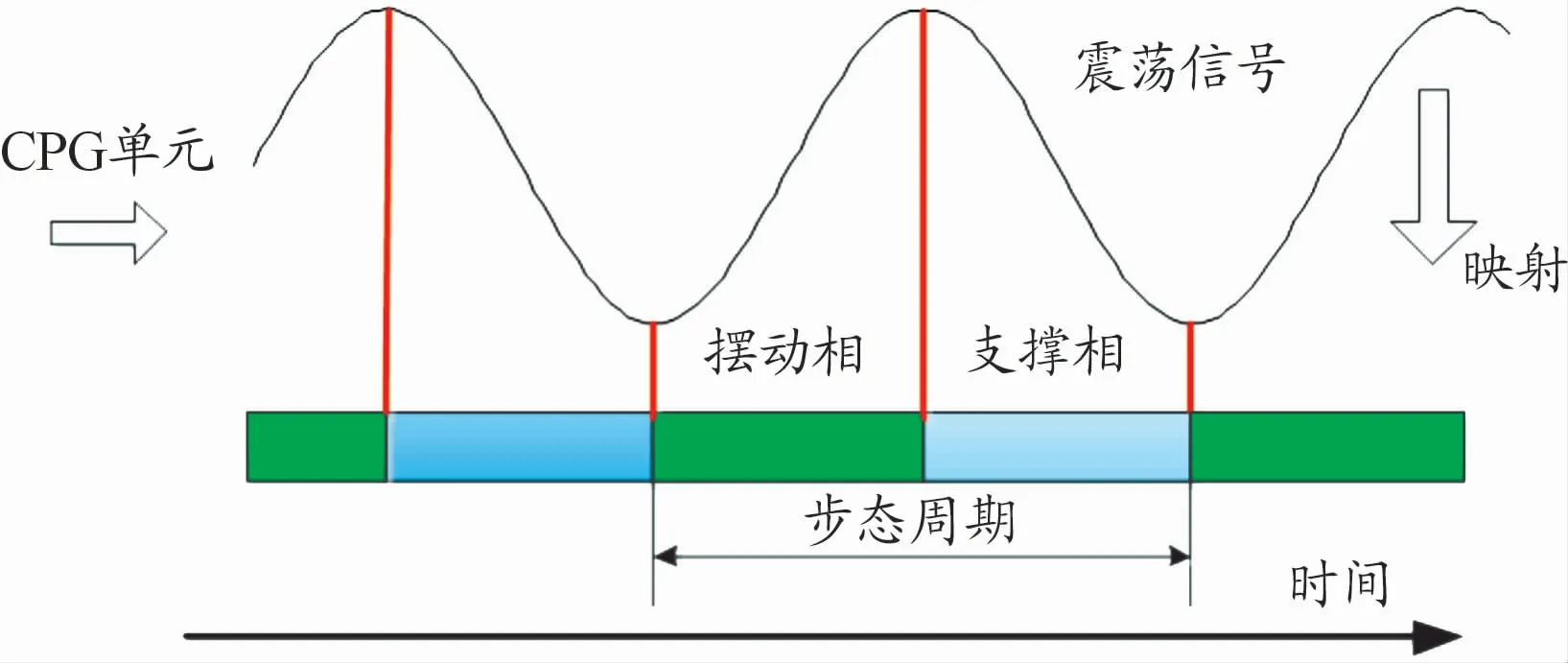
图6 CPG输出信号与步态之间的映射关系

2.2 四足机器人网络拓扑结构

由上述可知，CPG网络可实现生物自激行为生成的节律性运动［16］。CPG网络由多个中枢神经元组成，且由神经元之间的相互抑制产生节律信号并实现节律运动［17-18］。其中，CPG按照不同的连接方式可分为链式连接和网式连接，且具有以下优点：

①具有一定的自主控制能力，在脱离上层控制的前提下可以自主产生有规律的振荡信号，完成相应的控制任务。

②可产生不同的节律信号，实现不同的运动控制。

③能够接受外部信号的耦合，通过对外部信号的调节实现对节律运动的控制。

④结构简单，具有很强的适应性。

因此，如何构建足式运动机器人所需的稳定、适应性较强的节律运动是足式机器人运动控制的难点。为简化机器人的网络拓扑结构，机器人的4个全膝式腿关节采用4个Hopf振荡器进行描述，各腿之间采用4个振荡器进行表征，单腿髋-膝关节之间采用单向连接：振荡器的输出x做髋关节的角度控制信号，输出y经变换后作为膝关节的角度控制信号。因此，机器人CPG控制网络如图7所示，连接方式采用全对称进行连接；其中，LF、RF、RH、LH分别表示左前腿、右前腿、右后腿和左后腿。

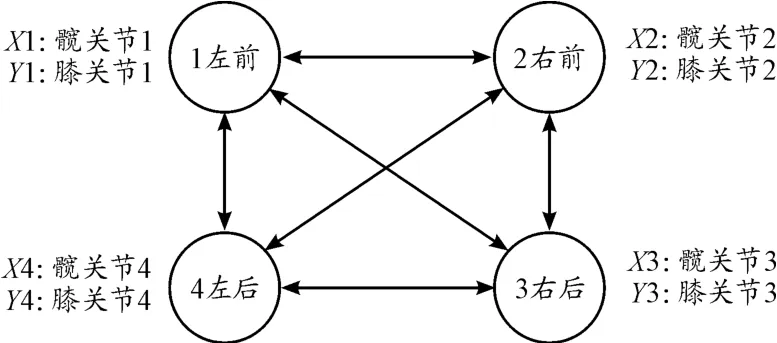
图7 机器人CPG控制网络

该CPG网络的数学模型及足内髋-膝关节控制信号如下：

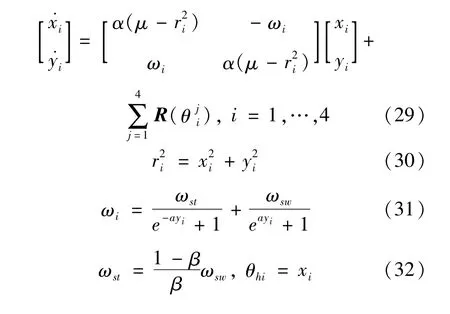
式中：Ak、Ah分别为髋、膝关节幅值；xi表示振荡器的输出，用作髋关节角度控制信号，且有θhi=描述振荡器间的耦合项，表示振荡器i、j之间的相对相位。R为CPG网络的连接权重，影响着CPG的输出形式，以实现机器人不同的步态，为旋转矩阵，表示振荡器之间的相位耦合关系。其他参数同式（28），此处神经元模型仅用于产生节律运动信号，故外部输入选项μ1=μ2=0。

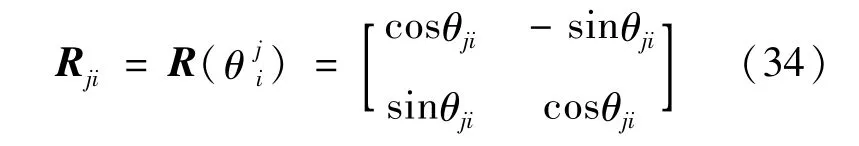
①摆动相：髋膝关节保持同步运动；髋关节摆动开始初期，膝关节逐步收缩；当摆动到幅值的中点时，膝关节收缩到最大；摆动的后期，膝关节开始伸展；当摆动到相位终点时，膝关节到达原始位置。

②支撑相：髋关节后摆时，膝关节基本保持不变。

依据上述假设，建立四足机器人足与足之间、足内髋-膝关节间的耦合关系，足内髋-膝关节耦合关系矩阵由Rhk表示，二者之间的连接权重矩阵为：

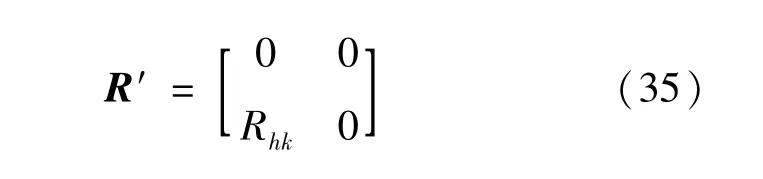
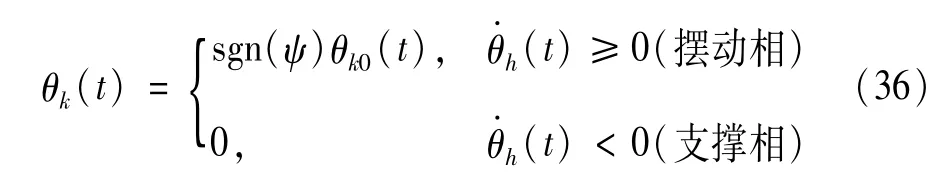
对该网络模型进行数值模拟，足间及足间模型输出如图8所示。

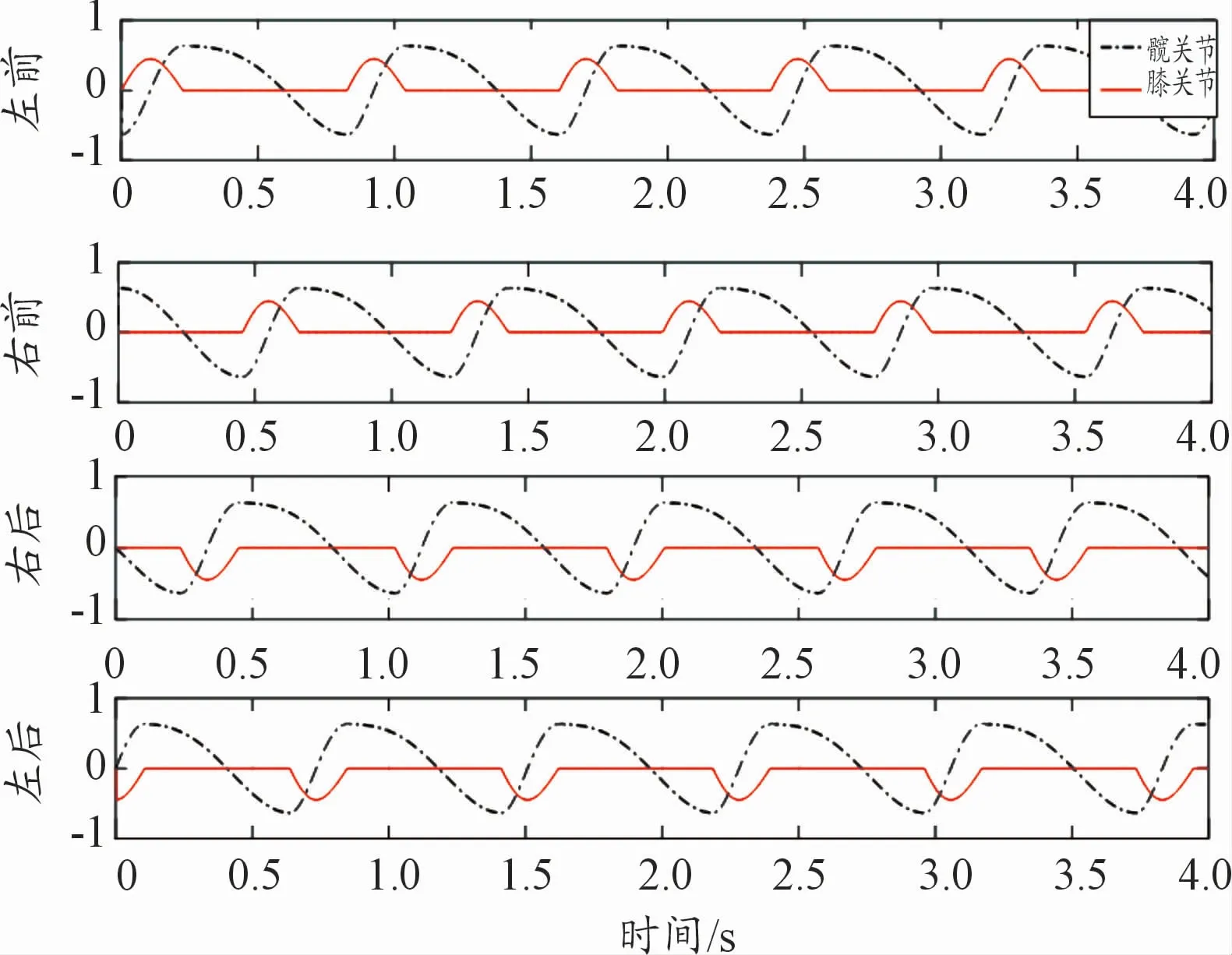
图8 机器人步态关节控制曲线

由图8可知，CPG控制网络模型所输出的髋关节控制曲线严格符合四足机器walk典型步态的相位关系，膝关节控制曲线到达稳态之后满足腿膝髋关节的运动关系。

3 仿真

为验证上述步态特征对四足机器人避障功能的有效性，对该四足机器人进行仿真分析。首先对四足机器人的平面行走进行验证，仿真时间设置2 s，步数为5；进而采用带有障碍物的路面进行Adams仿真分析，参数设置如下：仿真时间设置为25 s，步数为20。仿真步态表明：该四足机器人在实现避障的同时，步态调整曲线与前文假设髋膝关节运动关系证明了CPG控制网络的有效性。

1）平坦路面试验

平坦路面各足髋关节-膝关节相位运动曲线如图9所示。

图9 平坦路面各足髋关节-膝关节相位运动曲线

2）四足机器人避障仿真

障碍物设置圆柱1：半径45 cm，高30 cm；圆柱2：半径45 cm，高10 cm；依据上述的步态仿真特性，对机器人进行仿真分析，仿真结果表明：在保证稳定行走的前提下，髋关节和膝关节的变化曲线基本与CPG网络结构下的步态吻合（即摆动相时，髋膝关节同步启动，髋关节摆动前期，膝关节收缩，摆动中点时，膝关节收缩到最大；摆动后期，膝关节伸展；摆动中点，膝关节恢复原位），且能实现避障的功能，仿真环境、各足与膝关节的变化曲线如图10所示。

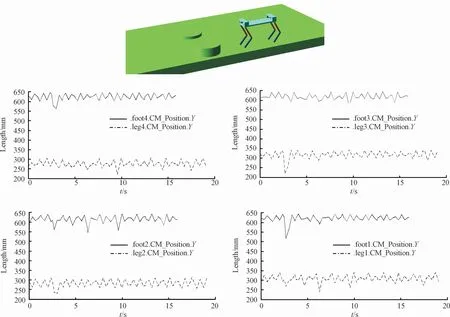
图10 避障运动中各髋-膝关节的变化曲线

4 结论

以四足机器人为研究对象，依据设计机器人的避障需求，首先对该机器人的结构进行全膝式关节配置设计，并基于机器人空间结构的数学基础，求解该全膝式机器人的运动学模型；结合CPG的仿生控制理论，采用Hopf振荡器对控制网络进行建模，并对该机器人的平面行走和避障行走2个方面进行了仿真分析。仿真结果表明：所提出的四足机器人可依据所处环境，协调四足之间的运动时序，维持平面行走的稳定性；在行走过程中遇到障碍物时，可调整四足的行走频率和相位，实现避障的功能，进一步拓展了生物控制在机器人中的应用深度。