基于数据驱动的车身不确定性优化方法

梁 源，许恩永，蒙艳玫

（1.广西大学 机械工程学院，南宁 530004；2.华中科技大学 机械科学与工程学院，武汉 430074；3.东风柳州汽车有限公司，广西 柳州 545005）

承载式车身是车辆最大的零部件，承载来自路面、侧向外力和车厢内部等各方面的作用力，使车身成为一个非线性耦合的结构体。针对车身的研究大多以车身处于近似线性条件下，各工况对车身的作用效果可叠加且易于分析，但较少考虑非线性因素对车身的影响［1］。然而，随着大数据技术的发展和计算能力的显著提高，为解决非线性问题提供了新的解决方法［2-3］。基于支持向量机的机器学习方法，采用序列最小优化算法，对车身在满载扭转工况、自由模态振动工况和车身侧倾工况下采集数据集进行车身应力和基频频率的分类和预测，以实现非线性结构的解耦。基于数据驱动和多目标遗传算法协同优化的方法，搜索解空间，在保持结构体力学性能的前提下优化各结构面特征尺寸。

基于不确定因素影响下的多目标优化问题，国内外已有不少研究成果。王岩等［4］利用结合Hammersley试验设计方法、RBF拟合方法和多目标遗传算法对车身关键零部件进行优化，提升了车身的动态性能，并通过实验验证了优化结果的正确性。Fang Y等［5］提出一种基于混合内核的支持向量机的回归方法，该混合内核结合了多项式核函数和粒子群优化算法，以解决单核支持向量在车身碰撞条件下处理非线性数据时无法涵盖数据特征的问题。Karimi M等［6］提出基于机器学习方法的元启发式算法，以解决输入参数的不确定问题，并通过实验证明了该方法的有效性。Ugo R等［7］提出基于数据驱动建立MPC预测模型的不确定性优化策略，该方法有效实现预测性能指标的最小化。Maity S等［8-9］提出一种不精确的多目标遗传算法以解决随机模糊环境下多目标商旅问题，采用经典MOGA、NSGA-Ⅱ和MOEA-D等多种算法求解多目标问题，对比结果表明所提出的方法具有优越性。从大量文献可看出，基于机器学习的数据驱动建模方法和智能优化算法相结合的嵌套优化方法，可以有效解决不确定条件下的非线性多目标优化问题，但是目前还没有一般性的方法适用于解决不同的具体问题。所以，车身在不确定因素影响下的协同优化方法仍然是值得研究的问题。

1 理论与方法

1.1 数据集的构成

数据集的构成对数据驱动建模的方法有很大影响，因此正确分析输入参数和输出参数的传递关系显得尤为关键［10］。承载式车身在车辆行驶过程中承受的载荷多变且运行工况复杂，对于车身设计和结构优化提出更高的要求。从静力学方面分析，在车身受力的4种典型工况中，满载扭转工况是车身产生应力最大的工况［11］。因此，选择满载扭转工况作为车身产生最大等效应力的第1种工况。从动力学方面分析，车身需尽可能避免低频共振，为此提高车身的基频是一种有效的解决方法。因此，选择自由模态振动作为车身的第2种工况。车辆在行驶过程中，由于车身侧倾的存在，车辆承受的侧向力发生转移，作用于车身的载荷产生明显的非线性作用。为较为全面地反映车辆在行驶过程中的承受不确定载荷的影响，选择车辆发生侧倾时车身产生的最大等效应力作为第3种工况。

车身的基频频率，即第一阶自由振动模态频率，是衡量车身动态特性的关键指标［12］。基频的测量原理如图1（b）所示，其中车身通过弹性绳悬挂于固定支架上。车身材料为B340LA钢，金属的模态阻尼很小，因此忽略阻尼对模态频率的影响。

车身和车轮的连接并非完全刚性连接，因此当车辆处于变形转向时，车辆会发生侧倾运动。相比于车身满载转弯工况，车身的侧倾运动考虑了侧向力、横摆力矩和侧倾力矩在一定区间范围内对车身的影响，把车身的受力系统从线性域扩展到非线性域。车身的侧倾工况等效动力学模型如图1（c）所示。由图1可知，车身的受力状态非常复杂，对于建立动力系统的目标函数非常困难。

为了解决在不确定因素影响下非线性系统目标函数难以建立、难以求解的问题，提出数据驱动建模的方法，为多工况下的车身建立分类模型。首先对模型进行参数化建模，基于拉丁超立方法构建车身的输入参数，进而分析车身处于图1的多工况条件下，分别获得不同结构面特征尺寸的最大扭转应力、基频频率和最大侧倾应力，以此构建数据集。其次，在车身结构满足使用要求的前提下，以车身各个面的特征尺寸作为输入参数，以车身的最大扭转应力、基频频率和最大侧倾应力建立分类标签，基于支持向量机的序列最小优化算法实现对数据集的分类。最后，构建分析模型进行输入参数的优化求解。

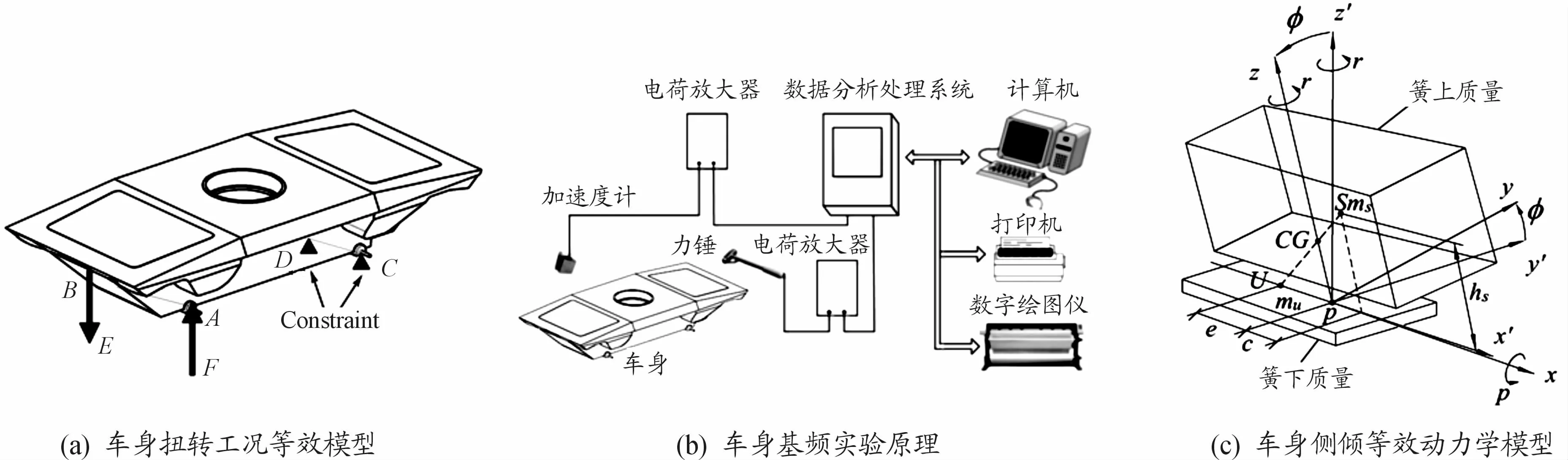
图1 车身多工况等效模型示意图

1.2 多目标问题的优化策略

不确定多目标优化问题的描述如下［13］：

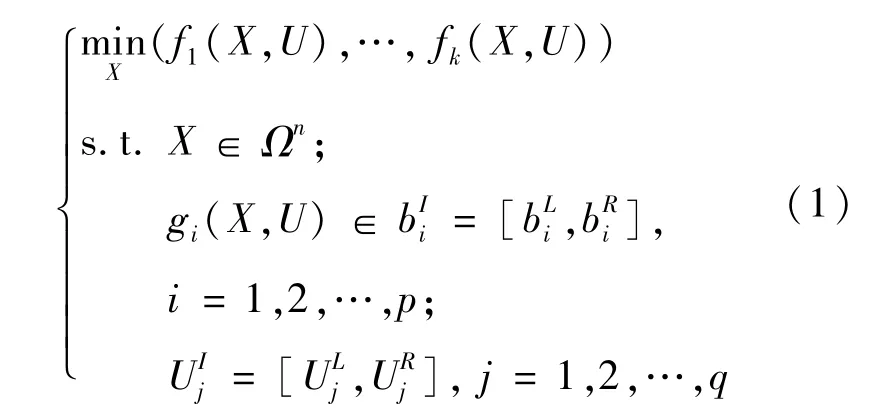
式中：X为取值范围为Ωn的n维优化变量；fk（X，U）和gi（X，U）分别为目标函数与约束条件；为第i个不确定约束所允许的区间；U为取值范围为UI的q维不确定变量。

在多输出分类问题中，为提高预测精度可尝试使用不同类型的支持向量机对数据进行分类［14］。这里二分类标签为｛-1，+1｝，分别代表负分类和正分类。对非线性支持向量机而言，序列最小优化算法是支持向量机学习算法的一种快速实现算法，把支持向量机的学习问题转化为求解凸二次规划的对偶问题［15-16］，如式（2）所示。

式中：xi∈Rn；yi∈y｛-1，+1｝；K（xi，xj）为正定核函数；α=（α1，α2，…，αN）T为拉格朗日乘子向量；C为参数。

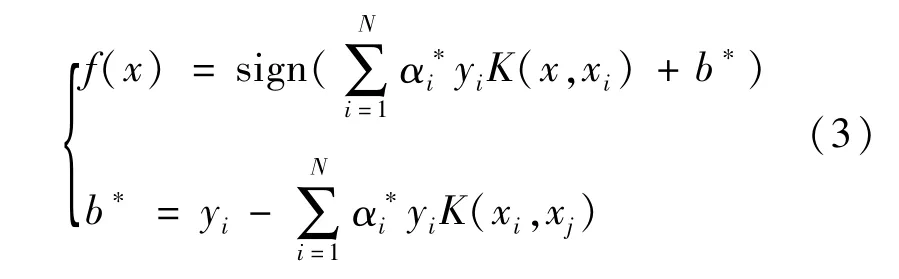
由于核函数为正定核，式的问题为凸二次规划问题，因此解是存在的。这里核函数使用高斯径向基函数，如式（4）所示。

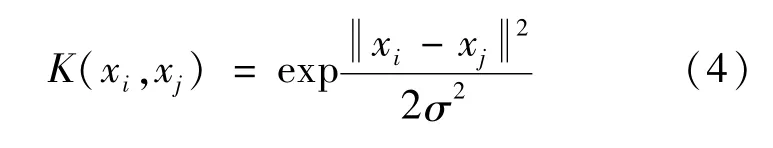
式中：σ是用户定义的用于确定达到率或者函数跌落到零的速度参数。

数据集分为训练集和测试集，当训练出较高精度的支持向量机分类器后，下一步就可以通过多目标遗传算法搜索解空间。初始种群经遗传、交叉和变异后产生新种群，使用分类器对新生成的解向量进行分类，直到遍历整个解空间，求出最优解，算法优化策略如图2所示。

从工程实际应用的角度考虑，结构的最大应力越小越好，基频频率越高越好。因此，对车身的最大扭转应力和最大侧倾应力而言，标签类期望取为“-1”，其物理含义是在相同工况下优化后的车身最大扭转应力和最大侧倾应力降低。同理，对车身基频频率而言，标签类期望取为“+1”，其物理含义是在相同工况下优化后的车身基频频率有所提高。

在种群进化过程中，对于符合分类器预测结果且满足期望的标签类，优先遗传给下一代种群，这会导致种群的个体xα（α=1，2，…，N）的值趋于增大。同时，种群通过遗传算法搜索整个解空间，求解xα的最小值，使xα的值趋于减小。所以当种群进化结束时，必定会存在满足SVM期望分类的个体x*，且该个体是解空间内满足期望分类条件下的最小值，即为最大最小意义下的最优解。

图2 基于数据驱动的不确定区间优化策略框图

1.3 不确定性模型的评价方法

模型不确定性包括模型结构的不确定性与模型参数的不确定性［17］。由于车身由许多零部件拼焊而成，导致焊接后的车身力学性能在一定范围内波动。另外，轮胎的侧偏特性和悬架系统产生的侧倾力矩等外作用力，造成车身实际受力处于非线性耦合状态，近似线性分析只在一定范围内拟合效果较好。这些不确定因素导致建立的近似模型和对系统建立目标等不能很好地解决不确定因素对系统的影响。

大多数不确定性工程问题多采用概率方法、模糊集方法和非概率方法描述。在非概率方法中，不确定因素上下界相对容易获取，因此采用区间方法描述不确定性问题［18］。

不确定性模型的评价方法参考朴素贝叶斯法对数据集的假设，即假设特征条件相互独立［19］。总体均值最小，表明自变量的特征尺寸总体最小，有利于实现车身轻量化。总体方差最小，表明每个变量与总体的差异最小，变量离散程度最小，有利于不同厚度板材的焊接。以解向量的均值和方差最小为优化的目标函数，表达式如式（5）所示。

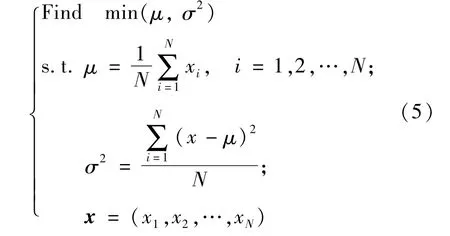
式中：μ为解向量的值；xi为解向量内各元素的值。

2 结果与分析

2.1 数值算例

为提高算法的运行效率，对车身结构面进行简化。该车身是用于装载农业机械臂的无人承载平台，车身结构既关于x轴对称又关于y轴对称，如图3所示。对车身进行参数化且使结构对称的结构面进行变量耦合，可以有效降低自变量的维数，这里特征尺寸构成的解向量为x∈（x1，x2，x3，x4，x5）T，被提取的结构面的5个特征尺寸的位置如图3所示。

图3 车身结构面特征尺寸示意图

样本集包含5个输入参数和3个输出参数，部分数据集如表1所示。在ANSYS Workbench环境下，在输入空间内输入200组数据，经过数值模拟获得对应的输出结果。

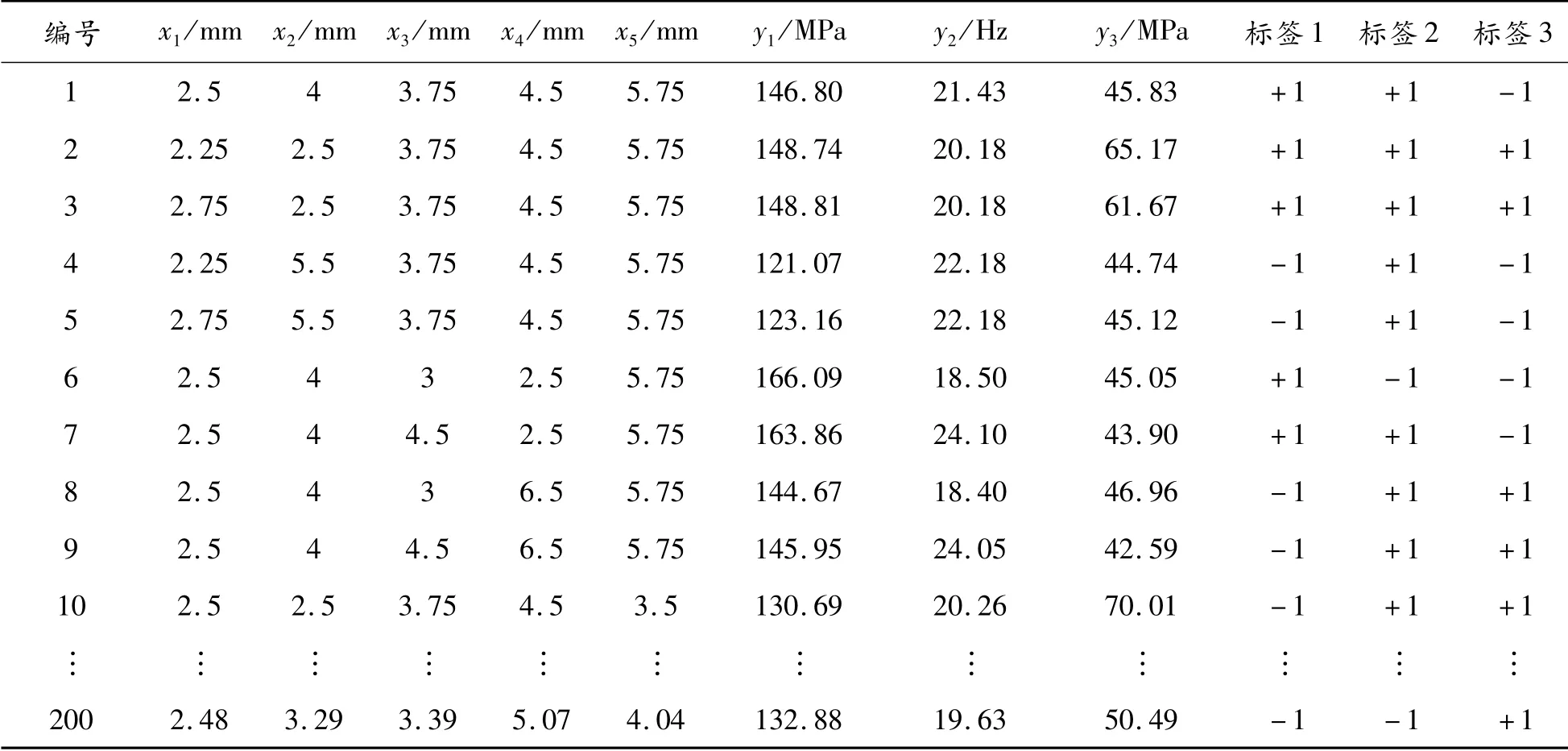
表1 数据集参数构成

数据集xα（α=1，2，…，5）组成输入参数，yβ（β=1，2，3）构成输出参数。为方便支持向量机对数据集进行训练，需要对输出参数进行二值化。这里采取的方法是：对每一个yβ设定一个阈值，yβ大于阈值的标签类记为“+1”，小于阈值的标签类记为“-1”。y1阈值设定为145.98 MPa，y2阈值设定为20.15 Hz，y3阈值设定为46.44 MPa。自变量优化值如表2所示。

表2 自变量优化值

为判断所选取的特征尺寸对优化结果的影响程度，根据表1的数据集分析所选取的特征尺寸的灵敏度。特征尺寸的灵敏度分析如图4所示。由图4可知，虽然特征尺寸xα的灵敏度高低有别，但是对不同的输出参数yβ均有重要影响。因此，需要对选取的所有的特征尺寸进行优化分析。

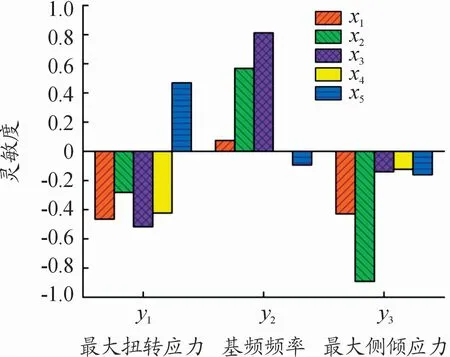
图4 车身特征尺寸灵敏度分析直方图

不确定优化模型除了考虑自变量因素，还考虑了不易准确测量的侧倾载荷F，F以一个变化的区间表示侧倾载荷的转移，这里F取值为7 840～11 760 N。另外，采取安全系数法确保其他不确定因素对结构安全的影响，这里安全系数取为1.0～1.2。

基于数据驱动的车身不确定性优化方法关键在于支持向量机需要达到较高的分类精度。根据Pedregosa F等［20］提出的方法对支持向量机进行参数调节，可以使分类精度达到93.33%。下一步，根据图2的优化策略进行优化。

多目标遗传算法的种群个体数量设置为40个，基于适应度排序法淘汰适应度较低的个体，采取随机抽样方式进行两点交叉，经变异后重组成新种群。按式（5）的评价方法评价种群的目标函数值。种群在进化至100代左右趋于稳定，如图5所示。

图5 种群随遗传代数的进化曲线

根据图2的优化策略，初始种群在解空间内随机生成，在种群进化开始阶段，最优个体的目标函数值可能趋于增大，随后目标函数趋于收敛。当种群进化趋于稳定时，模型可输出一系列Pareto解集，即多工况不确定因素影响下的最优解。Pareto解有若干个，这里选取一组Pareto解，经圆整后x*=（2.54，4.03，3.75，2.50，3.50）T。

2.2 结果分析

优化结果x*和初始值x0=（2.50，3.50，4.00，3.50，5.00）T相比，特征尺寸变化分别为+1.60%、+15.14%、-6.25%、-28.57%、-30%。所选取的特征尺寸总体均值减小11.78%，方差减小39.88%。根据优化结果重新设计车身结构面的厚度，为改善车身性能提供有价值的设计依据，尽可能发挥结构潜力。

为进一步验证优化后输出的解集x*是否正确，在ANSYSWorkbench环境下对x*进行数值模拟。材料选取B340LA，密度为7 850 kg·m-3，泊松比为0.27，屈服强度为410 MPa，弹性模量为2.1×105MPa。当x*=（2.54，4.03，3.75，2.50，3.50）T时，求解获得车身的最大等效扭转应力、基频频率和最大侧倾应力，如图6所示。

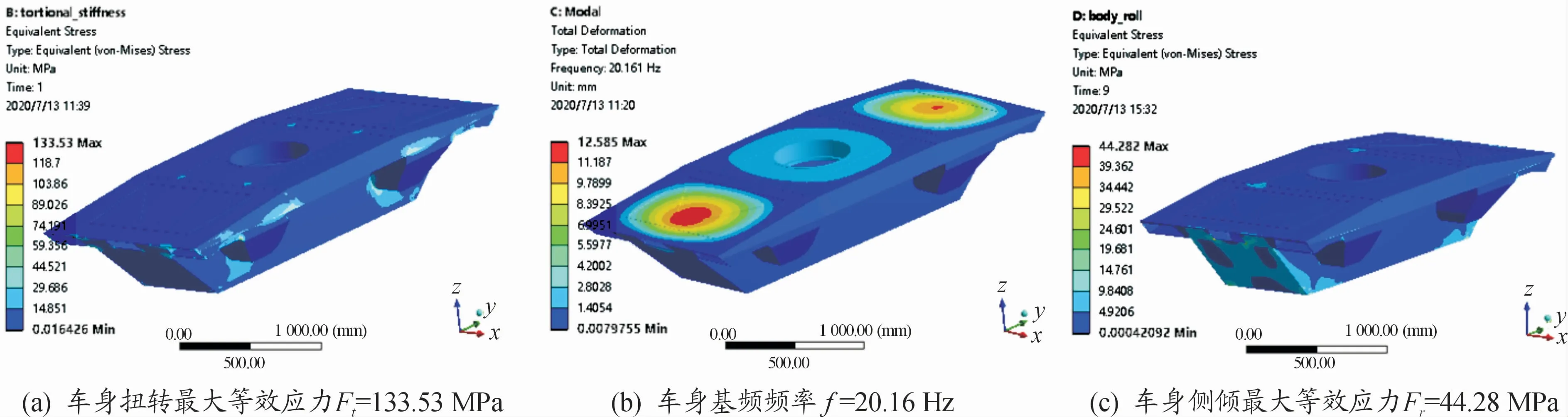
图6 车身多工况数值模拟结果

当优化结果为x*时，获得车身满载扭转的最大等效应力133.53 MPa＜145.98 MPa；基频频率20.16 Hz＞20.15 Hz；最大侧倾应力44.28 MPa＜46.44 Hz。由此可知，支持向量机的分类结果均正确，如表3所示。车身特征尺寸优化后可以使最大扭转应力下降8.53%，使最大侧倾应力下降4.65%，而且基频频率基本保持不变，优化结果较为理想。

表3 模型优化结果

3 结论

研究了车身在多工况下的不确定性优化问题。首先，基于支持向量机构建分类模型；其次，通过改进种群的重组方法，使支持向量机模型和多目标遗传算法进行数据交互，避免建立复杂的优化函数；最后，采用多目标遗传算法在解空间内进行全局搜索，使模型输出最优解。结果表明：所优化的特征尺寸总体均值减小11.78%，方差减小39.88%，而且车身优化后使最大扭转应力下降8.53%，最大侧倾应力下降4.65%。该优化方法不仅可以有效减小车身结构面的特征尺寸，而且可以进一步提高车身的力学性能。

基于数据驱动和多目标遗传算法相协同的优化方法较好地解决了处于不确定条件下车身的非线性优化问题，相比于确定性优化方法，可以最大程度地发挥车身结构的潜力，提高车身应对不确定性因素的稳定性。在不确定因素影响下，所提出的基于数据驱动和多目标遗传算法的协同优化方法是可行的。下一步将通过台架实验测量物理样机的实际参数，并与优化结果进行对比分析。