分布式驱动电动汽车横摆稳定性控制策略研究

2021-06-10李胜琴闫祥伟金丽彤

重庆理工大学学报(自然科学) 2021年5期

李胜琴，闫祥伟，金丽彤

（东北林业大学交通学院，哈尔滨 150040）

随着全球工业化蓬勃发展，环境污染问题和能源问题日趋严重。对汽车行业而言，针对能源和排放问题的技术改革最优方案就是纯电动汽车，同时伴随着人们日益增长的生活水平的需求，对于舒适性、操纵性和安全性要求更高［1］。分布式驱动电动汽车在轮胎纵向驱动力、侧向力等约束条件下，如何得到合理的直接横摆力矩，并将其分配给4个轮毂电机，对提高车辆横摆稳定性而言是急需解决的问题。

对于横摆稳定性控制策略的研究，大多集中在直接横摆力矩控制器的优化和轮毂电机转矩分配策略的优化。Semaan A等［2］根据神经网络原理，设计了一种人工神经网络，估计分布式轮毂电机提供车辆保持横摆稳定所需的直接横摆力矩。Gao等［3］针对分布式驱动电动汽车的横摆稳定性控制，基于线性时变径向基函数神经网络的转矩分配策略，结合轨迹跟踪算法，优化转矩分配。Chen等［4］提出一种基于模型预测控制的分布式驱动电动汽车轮毂电机转矩分配策略，分别基于能量效率的策略和基于最小功率损耗的策略来实施轮毂电机转矩分配。黄彩霞等［5］基于区域极点配置方法制定车辆横摆稳定性控制策略，分析并设计性能权重矩阵参数，提出以路面附着系数为依据的轮毂电机转矩分配策略。赵阳［6］提出在控制车辆的纵向和侧向稳定性同时，将集成能量管理作为控制目标，通过PSO算法优化通信序列，针对车辆不同制动工况，制定相应的制动力回收策略。张新锋等［7］针对分布式驱动电动汽车的横摆稳定性采用分层控制结构设计横向稳定性控制器。

基于积分滑模控制和线性滑模控制原理，设计直接横摆力矩控制策略，制定相应的轮毂电机转矩分配策略，通过对轮毂电机输出转矩的控制实现车辆横摆稳定性控制，实现分布式电动汽车横摆稳定性控制，具有一定的理论及实际应用价值。

1 整车参数化模型

1.1 基本车辆模型

利用Carsim软件车辆模型库中C-Class三厢车作为初始车型，按照国内某电动车车型参数，设置包括车体参数、传动系统、制动系统和轮胎参数的基本模型，并根据分布式驱动电动汽车非簧载质量和转动惯量较大的特点，适当增加二者的数值，用以模拟实际工况。

整车基本模型相关参数见表1，根据表中数据对车辆系统进行设置。

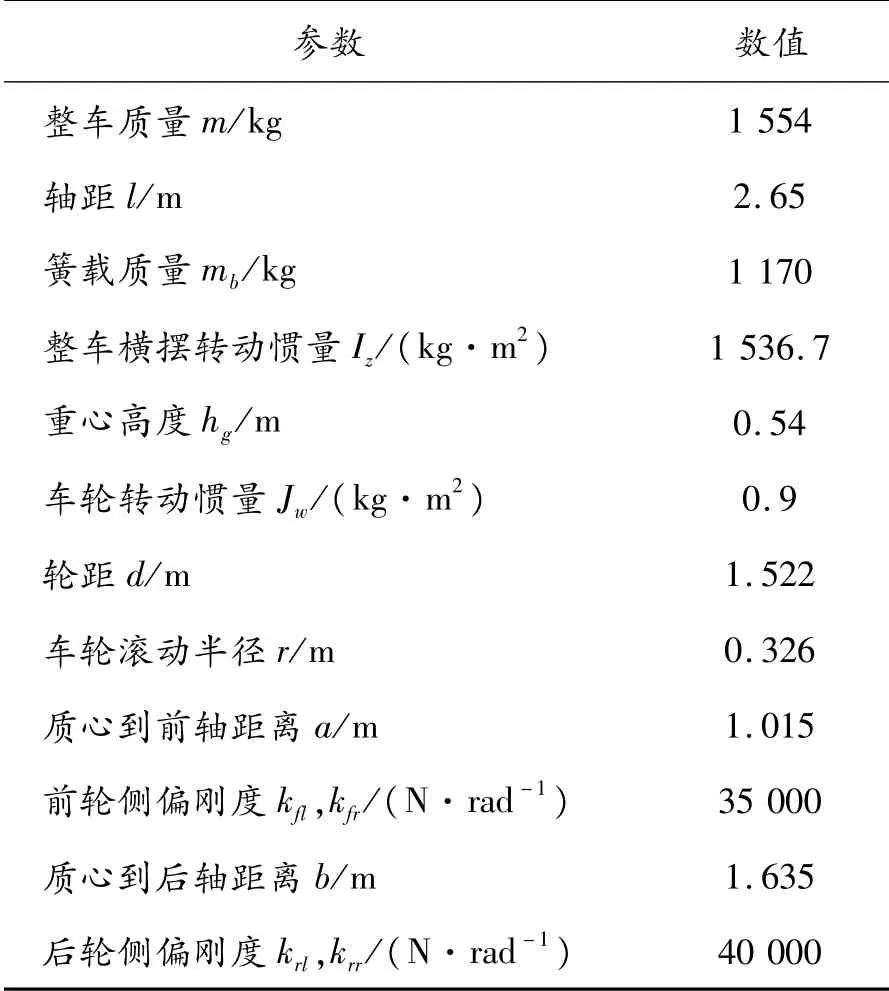
表1 整车相关参数

1.2 电机模型

分布式驱动电动汽车由电机控制动力输出，车辆的操纵稳定性由电机的动力性能直接决定。轮毂电机集成传动系、制动系功能，对于加速、减速和倒车等驾驶意图，均由电机改变输出扭矩完成。

1.2.1 电机参数匹配

电机参数需根据整车动力性能需求进行匹配，其中包括电机额定功率、峰值功率、额定转矩、峰值转矩、额定转速和峰值转速。

根据参考车型的相关参数和国标GB/T 28232—2012的相关试验内容，提出整车动力性需求指标，如表2所示［8］。

表2 整车动力性需求指标

车辆行驶时，4个电机总的需求功率Pall按式（1）计算：

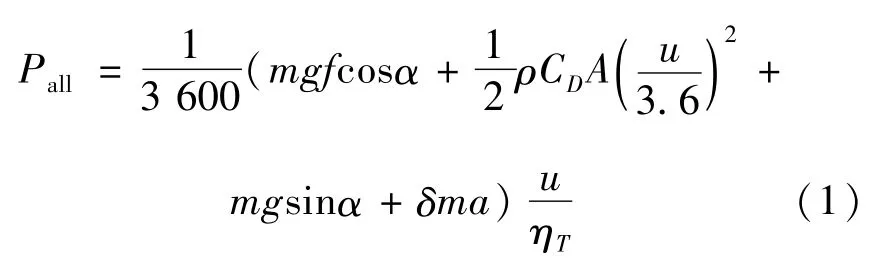
式中：g为重力加速度（m/s2），取9.8；F为滚动阻力系数，一般乘用车滚动阻力系数在0.01～0.02之间［9］，取值0.02；ρ为空气密度（N·s2·m-4），取1.225 8；CD为空气阻力系数，一般乘用车的空气阻力系数取0.28～0.4［10］，取值0.3；A为迎风面积（m2），参考电动汽车取值2.2；u为车辆行驶速度（km/h）；ηT为机械传动效率，由于轮毂电机直接作用于4个车轮，故可取值为1；α为爬坡度对应的坡度角；δ为车辆旋转质量换算系数，电动汽车取1.04［11］；a为车辆加速度（m/s）。

电机额定功率由车辆在平直路面上以最高车速行驶时的需求功率决定。电机峰值功率以最高车速所需功率、最大爬坡能力所需功率和最大加速能力所需功率共同决定。根据上述原则，结合表1、2和式（1），按照4个电机平均分配的原则，计算得到单个电机额定功率PN为9 kW，单个电机的峰值功率Pmax为21 kW。

车速和电机转速之间关系如式（2）所示：

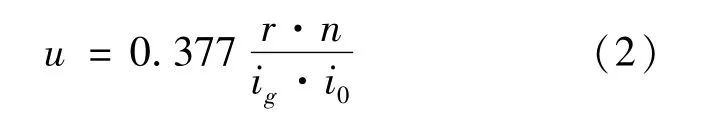
式中：ig、i0为变速器和主减速器传动比，由于电机直接控制车轮，因此均可设为1；u为车辆行驶速度（km/h）；n为电机转速（r/min）；r为车轮滚动半径（m）。则轮胎不打滑情况下，由式（2）可知电机最高转速nmax为1 200 r/min。

电机的基速一般指弱磁点的转速，基速以下电机在恒转矩区工作，基速以上电机在恒功率区工作，因此电机的基速也被称为额定转速。电机的基速比是指电机峰值转速与额定转速之比，一般取值2～4［12］，论文选取基速比为2.5。则根据电机峰值转速1 200 r/min，计算得到电机额定转速nN为480 r/min。

电机峰值转矩由车辆在低速、爬坡情况下输出的转矩确认。汽车在坡度角为14°、车速为20 km/h工况时电机峰值转矩Tmax为：

式中：amax为最大爬坡度对应的坡度角，25%爬坡度对应坡度角为14°；us为爬坡速度（km/h），取20 km/h。

根据式（3）计算，并考虑动力性余量需求，电机峰值转矩Tmax为400 N。

电机额定转矩TN按式（4）计算：

将电机额定转速、额定功率代入到式（4），算得电机额定转矩TN为180 N·m。

1.2.2 电机数学模型

由于本文中只研究车辆横摆稳定性的控制，电机仅作为提供车辆平稳运行所需的动力源，电机本身工作特性并不是研究重点，故对电机内部工作特性不做过多涉及，因此对电机模型进行相应简化。

引入电机时间常数tc，若不考虑电感和阻尼对电机产生的影响，则对于电机的需求转矩与实际转矩之间的关系可以简化为1阶传递函数如式（5）所示［13］：

式中：T为实际输出转矩（N·m）；Tm为需求转矩（N·m）。

2 横摆稳定性控制策略

选定横摆角速度与质心侧偏角作为表征车辆横摆稳定性的观测参数，制定控制策略，保证横摆角速度与质心侧偏角能够迅速恢复到相应期望值。通过整车模型和2自由度参考模型对比得到实时观测参数增益，提供给直接横摆力矩控制器，得到相应的直接横摆力矩期望。选择滑模控制方法，设计积分滑模直接横摆力矩控制器和线性滑模直接横摆力矩控制器，依据车辆横摆稳定性要求，设计轮毂电机转矩分配控制器，将控制器得到的直接横摆力矩期望值分配给4个轮毂电机，实现轮毂电机控制。

2.1 2自由度参考模型

选择横摆角速度和质心侧偏角作为车辆稳定性识别参数，为了便于得到车辆稳定状态时的横摆角速度与质心侧偏角理想值，一般将整车模型简化为2自由度模型如图1所示。假定车辆纵向速度为定值，只考虑车辆沿y轴的侧向运动与绕z轴的旋转运动，此时需满足如下条件：

1）车辆质心为车辆坐标原点；

2）忽略悬架系统影响，不考虑转向系统的影响，车辆左右两侧前轮转角相同；

3）忽略侧向风的影响；

4）4个轮胎型号相同且动力学特性相同。

图1 2自由度模型示意图

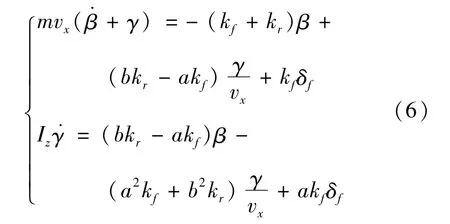
式中：vx为车辆纵向速度（m/s）；vy为车辆侧向速度（m/s）；γ为车辆横摆角速度（rad/s）；β为质心侧偏角（rad）；kf、kr为车辆前、后轮胎侧偏刚度（N/rad）；δf为前轮转角（rad）；Iz为车辆绕z轴的转动惯量（kg·m2）。

由于轮胎侧向力受到轮胎与路面的附着力极限制约，因此横摆角速度和质心侧偏角的最大值为：

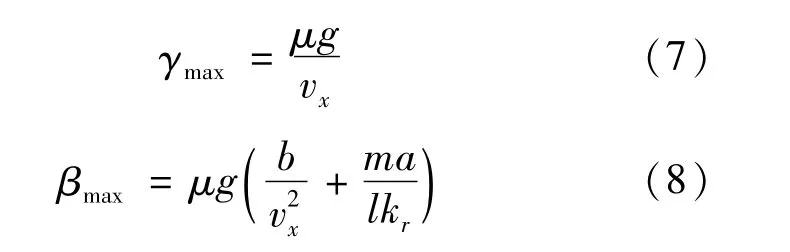
式中：μ为路面附着系数。

当系统稳定时，结合式（6）～（8）得横摆角速度和质心侧偏角的期望值为：

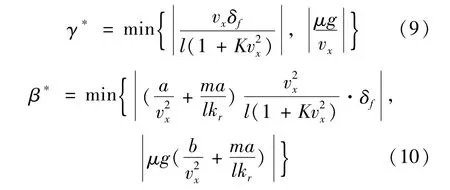
2.2 积分滑模直接横摆力矩控制器

设横摆角速度与质心侧偏角增益为e=［e1，e2］，其中e1=Δβ，e2=Δγ。根据式（6），增加1个额外的补偿力矩ΔM，得到提供补偿力矩后的车辆瞬时状态方程：

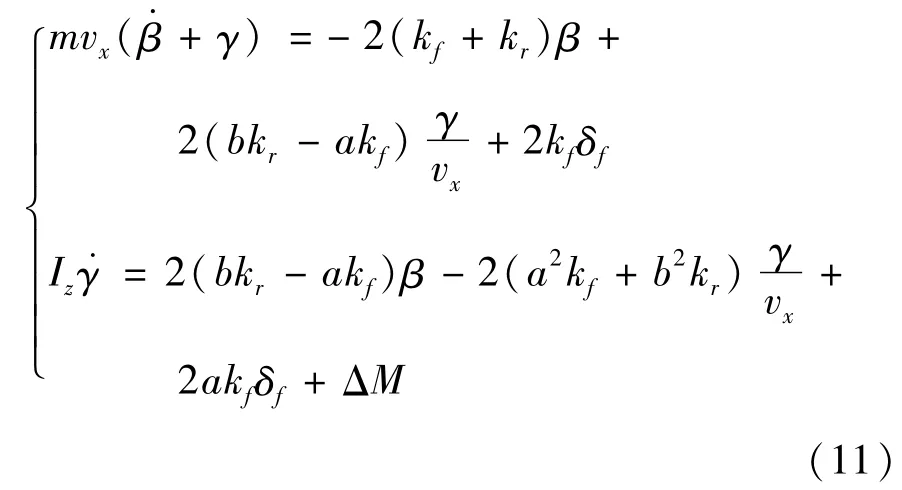
式中：ΔM为直接横摆力矩期望（N·m）。

转化为状态空间方程如下：

将相关参数代入式（8）可得：

设滑模面为：

则状态空间方程表示为：

由式（12）可知，目标由控制β与γ趋近于β*与γ*转化为控制二者增益e趋近于零。则对于v函数来说，可以设为：

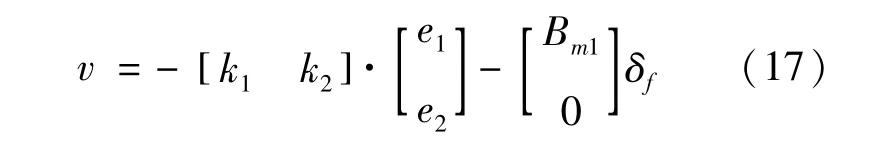
选择李雅普诺夫方程为：

最终得到直接横摆力矩控制器为：

2.3 线性滑模直接横摆力矩控制器

设滑模面为：

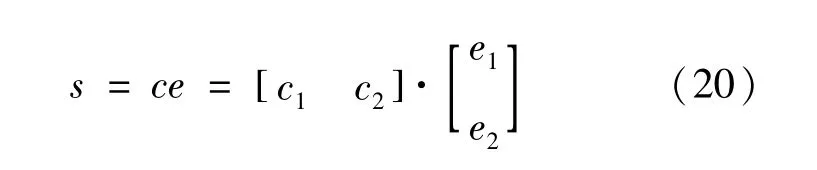
式中：c1、c2为常数。

根据李雅普诺夫方程为：

将式（20）（21）代入式（11）可得：

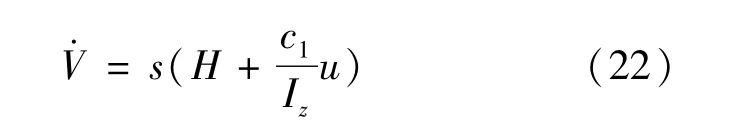
式中：

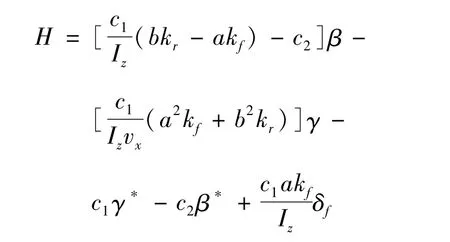
由式（22）可得：

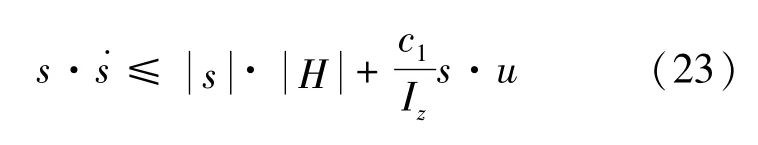
由李雅普诺夫直接方法的系统稳定可控需满足的条件，结合式（22），可得：

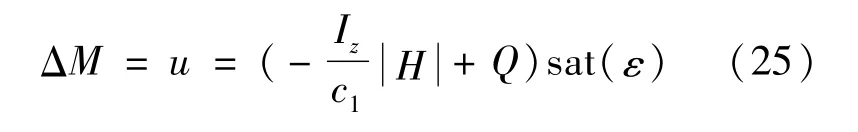
2.4 轮毂电机转矩分配控制器

考虑电机特性、路面附着系数等约束条件，寻找相应优化目标，形成多目标约束寻找最优解的分配方式，并选择罚函数法进行分配计算。

2.4.1 优化目标

为表征车辆稳定性要求，考虑到车辆行驶工况的非线性特性，可将轮胎附着率的平方和作为优化目标函数：

式中：Fxi为路面提供纵向力（N），其中i=1、2、3、4（左前、右前、左后和右后）；Fyi为路面提供侧向力（N）；Fzi为路面提供垂向力（N）。

2.4.2 约束条件

1）直接横摆力矩约束

轮毂电机转矩分配实际上是将控制器得出的直接横摆力矩期望值进行再次分配的过程，因此依据各轮所受轮胎纵向力对质心形成的横摆力矩，建立约束函数：

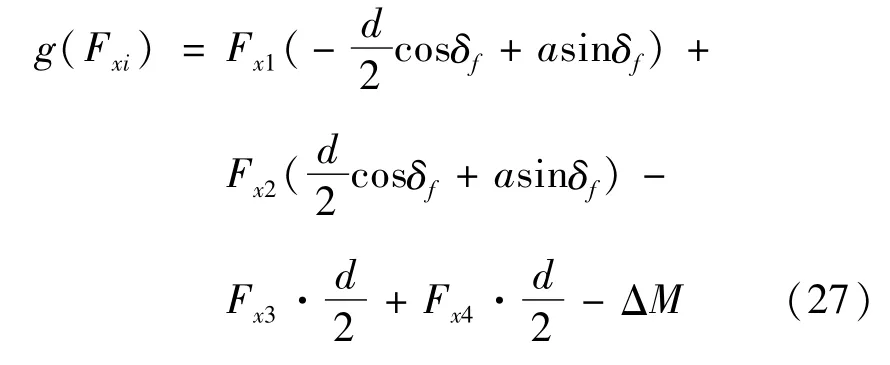
2）轮毂电机峰值转矩约束

驱动轮毂电机本身受到蓄电池、电压、温度和反应时间等的影响，每个电机提供的最大输出转矩均需要设置相应的限制，建立约束函数：

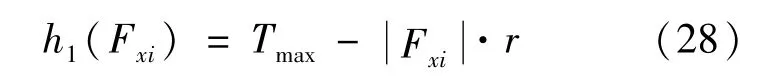
3）路面附着系数约束

在轮毂电机转矩分配策略中需要设计可按照不同路面状况制定分配策略的约束条件，建立约束函数：

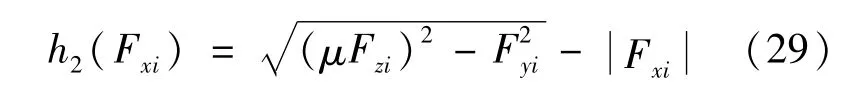
构建罚函数如下：

对式（30）中Fx1、Fx2、Fx3、Fx4进行微分偏导得出▽L，并令▽L=0。用数值迭代法求最优解设ψ初始值为1，并在迭代过程中使ψ不断减小且趋近于零，求出min L（Fxi，ψ）的最优解。

得到各轮毂电机最优纵向力后按照式（31）进行计算得到，然后将需求转矩提供式（5）的电机模型，由电机模型输出实际转矩提供给各驱动轮。

式中：Tmi为电机需求转矩（N·m），i=1、2、3、4（左前、右前、左后和右后）。

3 控制策略仿真验证

综合车身模型、电机模型、直接横摆力矩控制器模型和轮毂电机转矩分配控制器模型，建立联合仿真模型，分别选取双移线工况和鱼钩工况进行仿真试验。

为了对所提出的滑模控制策略进行验证，分别进行了无控制、传统模糊PID控制、积分滑模控制和线性滑模控制几种策略下车辆的仿真试验，对车辆的横摆角速度和质心侧偏角进行对比分析。

3.1 双移线工况

根据双移线试验标准ISO 3888-1-1999，方向盘转角输入设置如图2所示，选取路面附着系数为0.85的干燥沥青路面，测试车速为120 km/h，仿真时间为12 s［14］，仿真结果如图2～4所示。

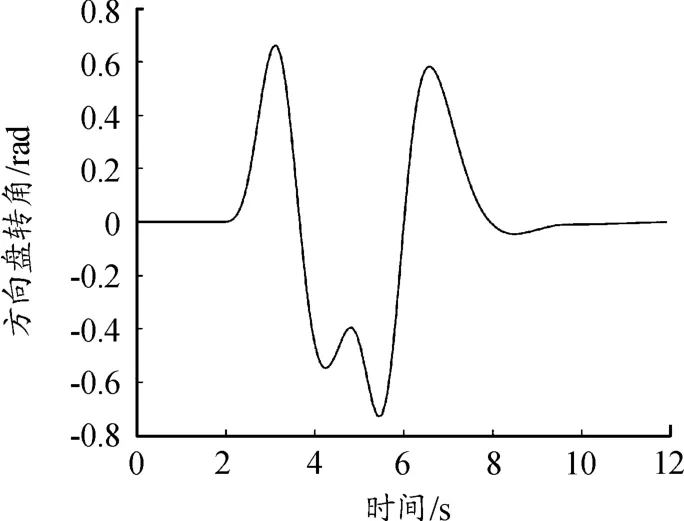
图2 方向盘转角输入

图3、4是在双移线工况中，车辆横摆角速度和质心侧偏角的变化曲线。

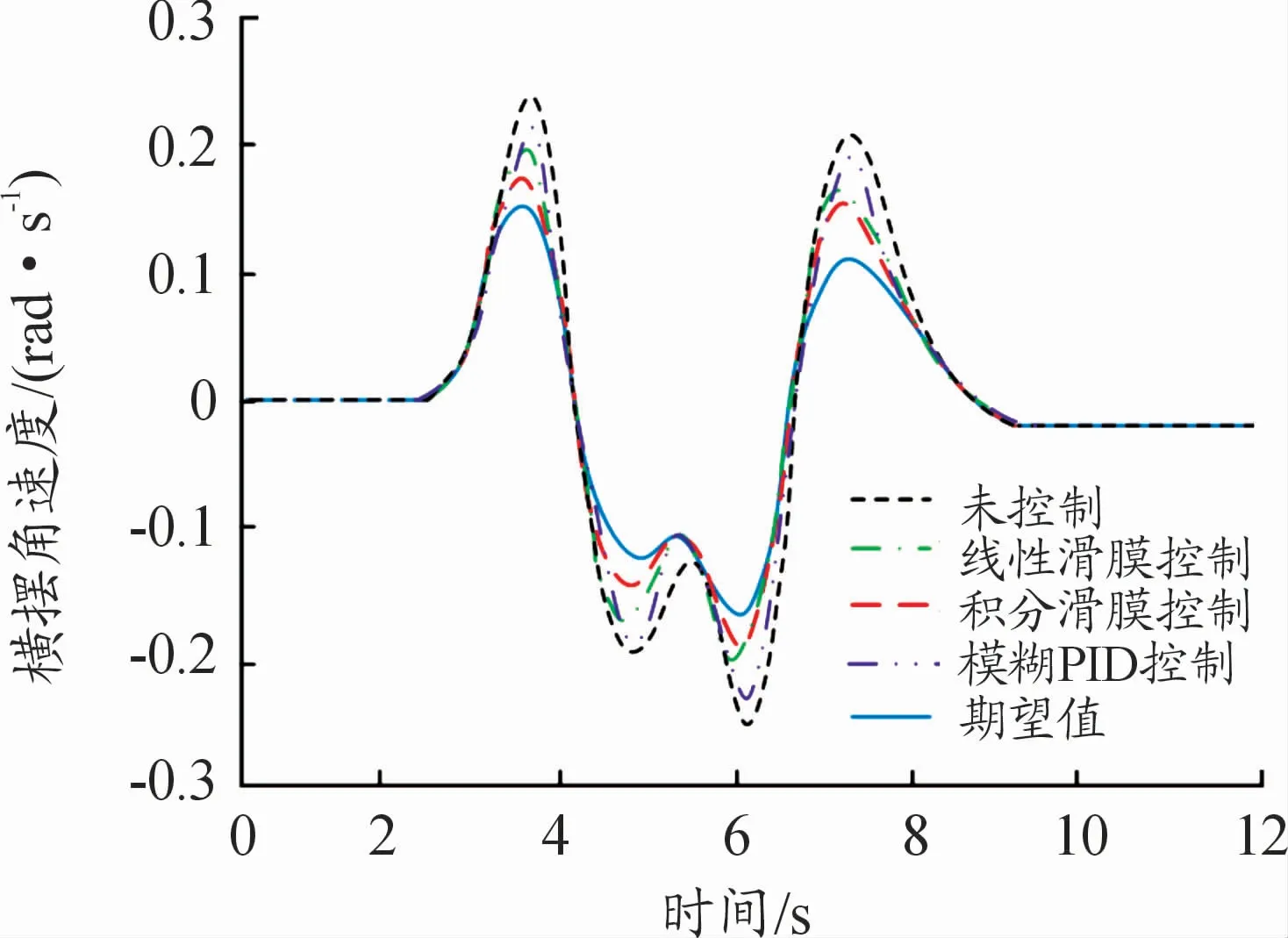
图3 横摆角速度曲线

图4 质心侧偏角曲线

在未施加控制时，横摆角速度和质心侧偏角均偏离期望值变化轨迹，在3.5 s时横摆角速度达到最大值0.24 rad/s，0.5 s后质心侧偏角达到最大值-0.047 rad。施加积分滑模整车控制策略和线性滑模整车控制策略后，横摆角速度和质心侧偏角迅速减小至期望值，并沿着期望值轨迹变化，横摆角速度最大值分别为0.17、0.20 rad/s；质心侧偏角最大值分别为-0.038、-0.040 rad。2种控制策略均能有效对车辆稳定性进行控制。

图5、6是双移线工况中，车辆的行驶轨迹曲线和各轮毂电机输出转矩的变化曲线。可以看出：施加积分滑模、线性滑模和模糊PID控制策略后，车辆的行驶轨迹横向位移最大值分别为3.66、3.78、3.80 m，均小于未施加控制时的最大值，回正速度变快，且滑模控制的2种控制策略均优于模糊PID控制策略。轮毂电机转矩分配策略可以保证施加有效的直接横摆力矩，对车辆横摆稳定进行控制，使得整车横摆稳定性控制策略能发挥较好的作用。

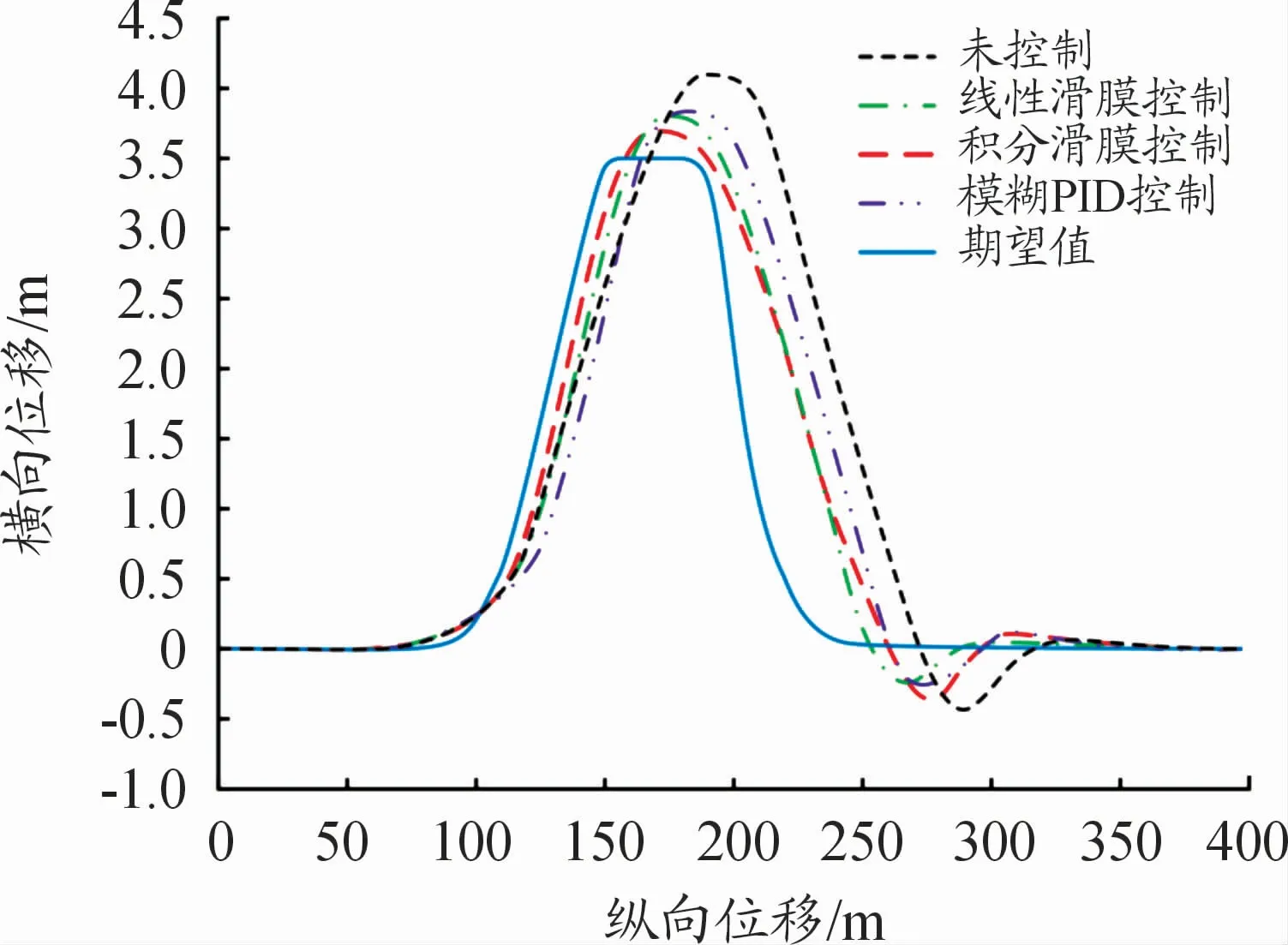
图5 行驶轨迹曲线

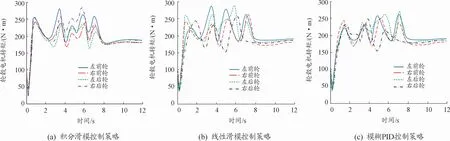
图6 轮毂电机转矩变化曲线

3.2 鱼钩工况

美国NHTSA新车评定规程中NO.NHTSA-2001-9663文件规定，方向盘转角输入如图7所示［15］，仿真试验结果如图8～11所示。

图7 鱼钩试验方向盘转角输入曲线

图8 、9是在鱼钩试验工况中，车辆横摆角速度和质心侧偏角曲线。施加积分滑模控制和线性滑模控制策略后，横摆角速度和质心侧偏角迅速减小至期望值，并沿着期望值轨迹变化，横摆角速度最大值分别为0.23、0.24 rad/s，小于未控制的0.28 rad/s；质心侧偏角最大值分别为0.041、0.042 rad，小于未控制的0.083 rad。3种控制策略均能有效对车辆稳定性进行控制，而对滑模控制策略和模糊PID控制策略的效果进行比较，滑模控制的2种控制策略控制速度更快，控制效果也更好。

图10、11是鱼钩工况中，车辆的行驶轨迹曲线和各轮毂电机输出转矩的变化曲线。

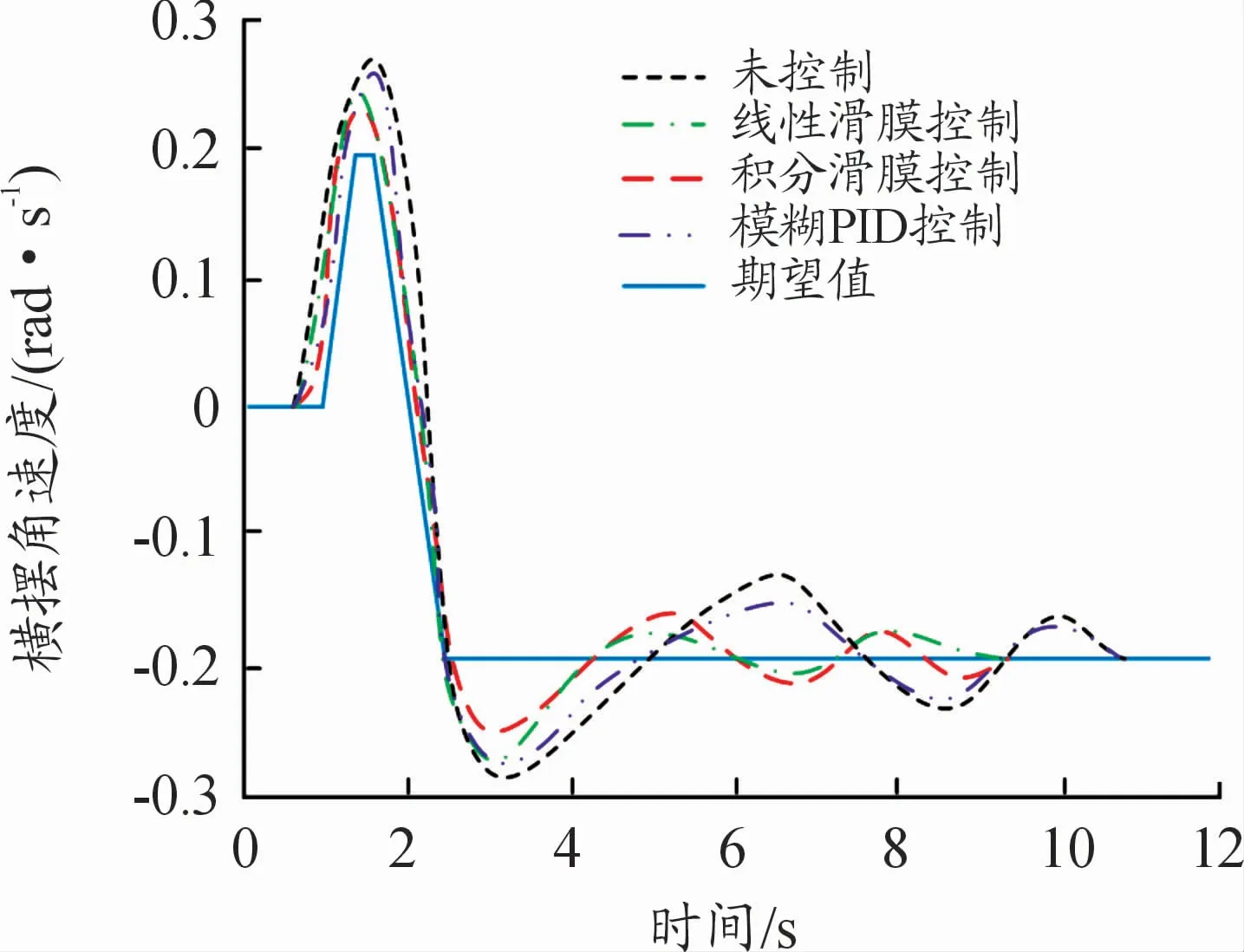
图8 横摆角速度曲线

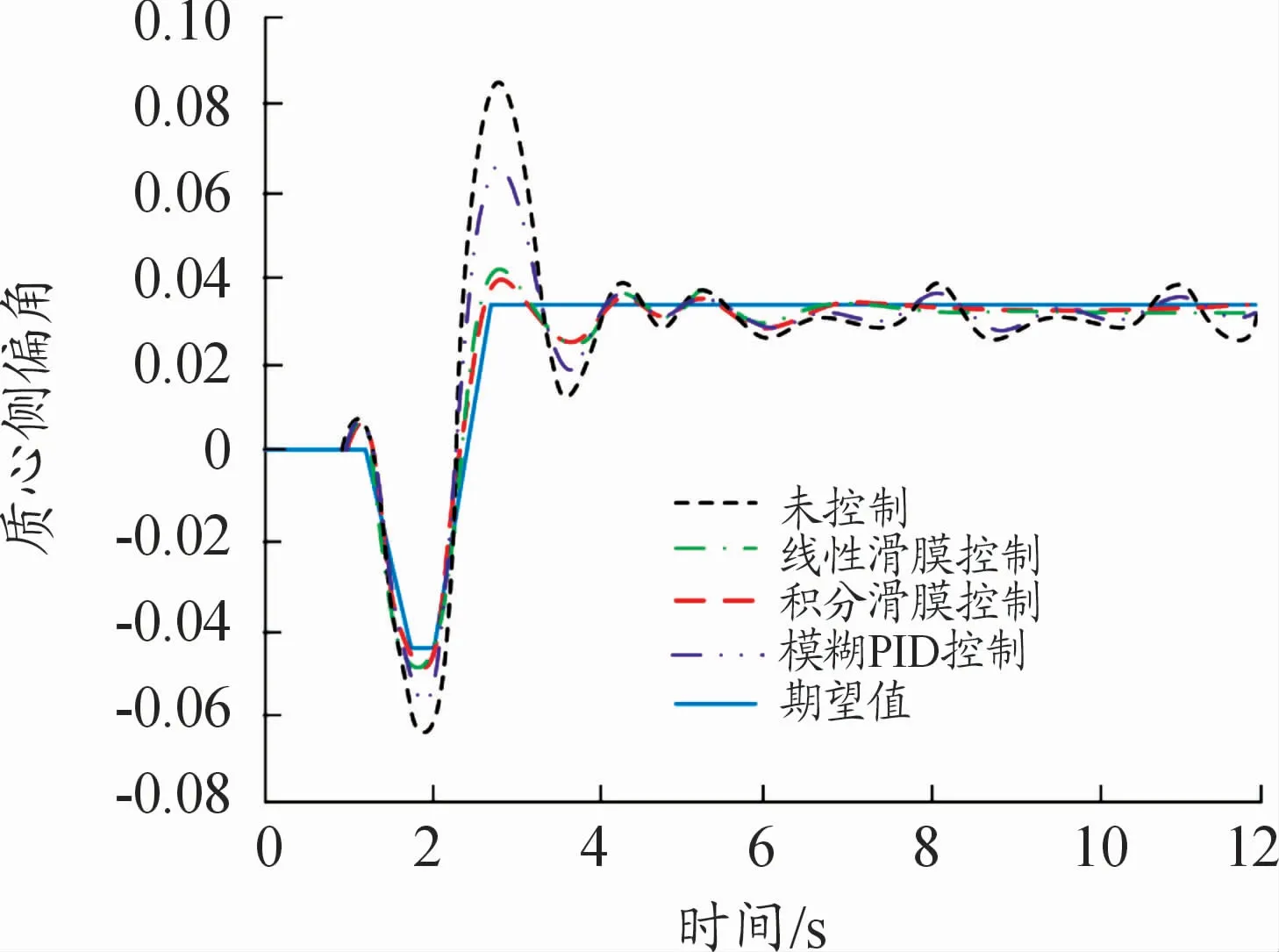
图9 质心侧偏角曲线

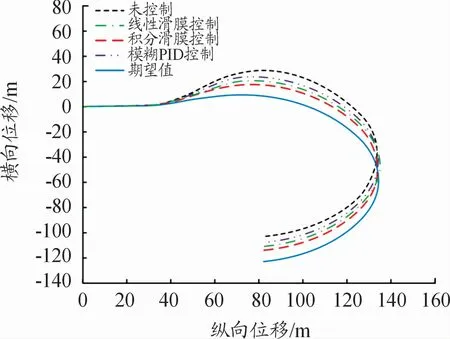
图10 行驶轨迹曲线

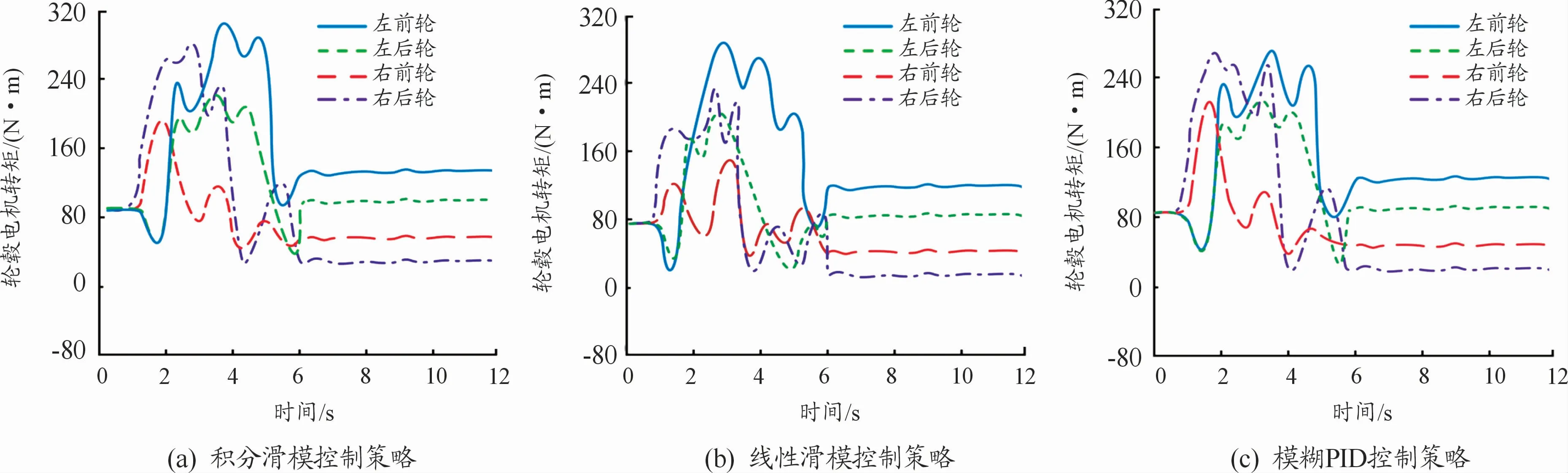
图11 轮毂电机转矩变化曲线

当车辆未进行控制时，车辆的行驶轨迹与期望轨迹差距较大，横向位移最大值为28.2 m。行驶方向发生较大变化。施加积分滑模、线性滑模和模糊PID控制策略后，车辆的行驶轨迹横向位移最大值分别为18.6、20.3、22.1 m，均小于未施加控制时的最大值，行驶轨迹修正效果明显，且滑模控制的2种控制策略均优于模糊PID控制策略。轮毂电机转矩分配策略可以保证施加有效的直接横摆力矩对车辆横摆稳定进行控制。