一类常微分方程的解及其应用

吕桂稳， 王雅茹,薛志群

(石家庄铁道大学 数理系，河北 石家庄 050043)

0 引言

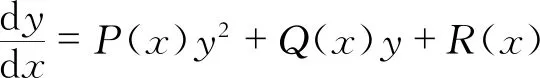
然而在现代微分方程的研究与应用中，很少求微分方程的通解或所有解。一是因为只有少数微分方程可以求出其通解或所有解，二是有些问题不需要通解或所有解。但是对初学者尤其是非数学专业的学生来说，微分方程的解的概念还是非常重要的。因此，在一些通用教材中仍把微分方程的通解、所有解、特解等作为基本概念来一一介绍。

1 微分方程的通解、所有解、特解等基本概念及其关系

文献[1]中有这样的定义:对于n阶常微分方程

F(x,y,y′,L,y(n-1),y(n))=0

(1)

如果将函数y=φ(x)代入方程(1)后，能使它变为恒等式，则称y=φ(x)为方程(1)的解。

含有n个独立的任意常数c1,c2,LLcn的解y=φ(x,c1,c2,LLcn)称为n阶方程(1)的通解。

把满足初值条件的解称为微分方程的特解[1]。

文献[2]中对微分方程通解的定义是这样的：设函数y=φ(x)在区间I上有n阶连续导数，如果在区间I上F(x,φ(x),φ′(x),L,φ(n)(x))=0，则称函数y=φ(x)是微分方程的解。如果微分方程的解中含有任意常数，且相互独立的任意常数的个数与微分方程的阶数相同，那么确定了通解中的任意常数以后，就得到微分方程的特解[2]。

文献[1]、文献[2]中对通解的定义是一致的，而且在本质上特解都是利用通解，通过初始条件确定的。然而对于一个微分方程来讲，大多数情况下它的解并不唯一，那么使某个微分方程成为恒等式的全部函数，称为这个方程的所有解。一个微分方程的解、通解、特解及所有解具有如下关系。

定理1 通解、特解都是微分方程的解，但微分方程的通解未必是它所有解。

情形1 对微分方程进行变形的过程中可能会丢掉解，致使通解不是所有解。

情形2 对微分方程进行变形过程中，丢掉的解会通过对通解中任意常数的选取又补回来，这时候通解又是所有解了。

例2 求微分方程y′+P(x)y=0的所有解，其中P(x)是连续函数。

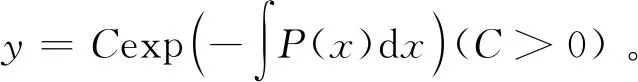
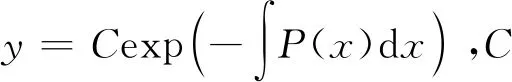
由情形1、2可知，变量可分离的方程，齐次型和准齐次型方程，伯努利方程等在解方程的过程中要进行变形，因此它们的通解可能不是所有解。而对于全微分方程、常系数线性齐次和非齐次方程的通解都是所有解。

情形3 方程的解既不是通解也不是特解，又不包含在通解中。

例3 求解微分方程(y′-1)(yn-1)=0。

解：显然y=x+C和y=C1e-x+C2ex都是它的解，由定义，y=C1e-x+C2ex是微分方程的通解，而y=x+C既不是通解也不是特解。

定理2 微分方程通解中的任意常数是指在一定范围内的“任意”。

定理3 满足初值问题的特解不一定唯一。

2 一阶非齐次线性微分方程特解的一个求法及其应用

一般情况下，求初值问题的特解，需要求出方程的通解，根据初值条件确定任意常数，从而得到特解。但是有些方程要具体问题具体分析。

例6 证明一阶线性微分方程y′+P(x)y=Q(x)，满足初始条件y(x0)=y0的情况下，它的特解为

(2)

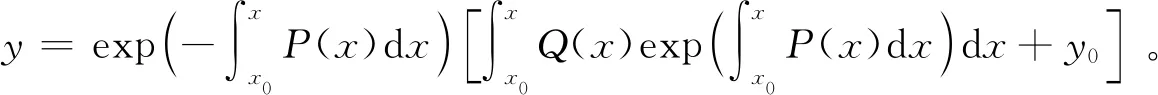
(3)

注：由这个方程的解,即式(3)，得到了次谐Melnikov函数，从而用Melnikov方法，得到了非线性碰撞系统

(4)

出现混沌的条件[4]。