一种架空轨道穿梭车的参数优化与仿真分析
2021-06-10彭孟菲郭文武邢海军韩彦军
彭孟菲, 郭文武, 邢海军, 韩彦军, 李 航
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
0 引言
有轨运输设备具有运量大、速度快和适应性强的特点,在多种工业场合都有广泛应用,例如仓储运输中的有轨制导车辆[1]、隧道施工中的进料和出碴[2]等。这些运输设备的轨道通常铺设在地面,并且往往需要配以辅助卸料设备,或通过人工方式卸料。本文研究了一种架空轨道穿梭车(如图1(a)和图1(b)所示),该穿梭车可用于矿井运输、预制混凝土构件生产线和无人仓库等多种工业场合,并且可以通过简单的结构进行自动卸料。该穿梭车主要由控制单元、行走机构、盛料和卸料机构组成,其简化模型如图1(c)所示,其中各参数符号含义见表1。
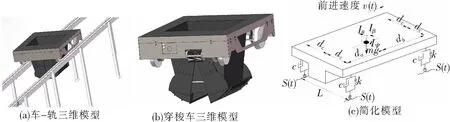
图1 穿梭车模型

表1 穿梭车主要参数
穿梭车在行驶过程中,轨道垂向不平顺引起车身垂向振动,垂向振动的幅值过大将影响车运行的安全性,悬架的弹性元件与阻尼元件能够对车身的垂向振动进行有效隔离,称为消极隔振[3]。此外,较快的车速也会引起垂向振动过大,为了尽可能提高车辆穿梭工作的效率,应要求空载返程速度尽可能快,因此,确定合适的悬架参数是设计该穿梭车的关键。通过H2优化确定了使车身垂向振动能量最小的刚度和阻尼参数,并利用数值方法对1/4车模型进行验证。最后通过Simpack建立了整车模型,利用根轨迹法计算了整车模型在轨道不平顺激扰下车失稳的临界速度。
1 简谐激励下车身的垂向振动
首先考虑1/4车模型以及轨道垂向不平顺为谐波的情况,其动力学模型如图2所示。设车速为v,路面激励波长为l,幅值为α,则轨道垂向激励可表示为
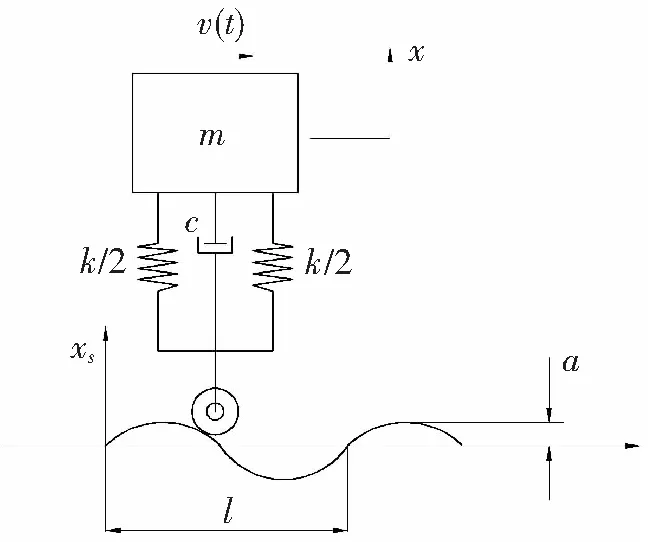
图2 1/4车模型
(1)
由达朗贝尔原理,车身的垂向振动微分方程为
(2)
式中,m、c、k分别为车的1/4质量、阻尼系数和刚度系数。
将式(1)代入式(2),稍加整理可以得到
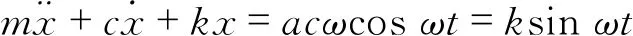
(3)
式中,ω为轨道不平顺对车轮的激励频率,ω=2πv/l。
由线性系统的振动理论[3],车身垂向振动的稳态响应,即式(3)的特解为
(4)
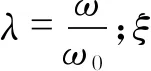

2 悬架参数优化
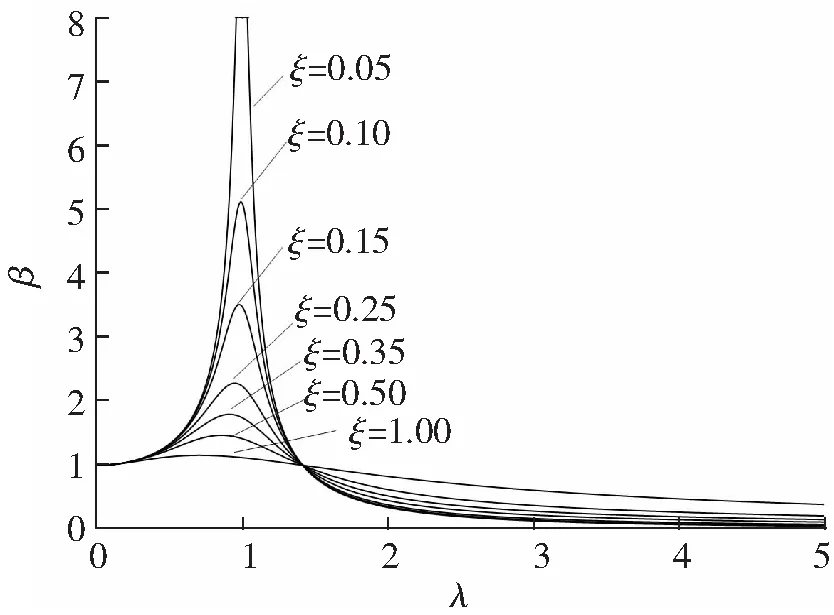
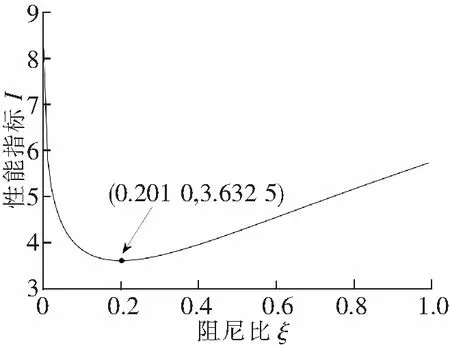
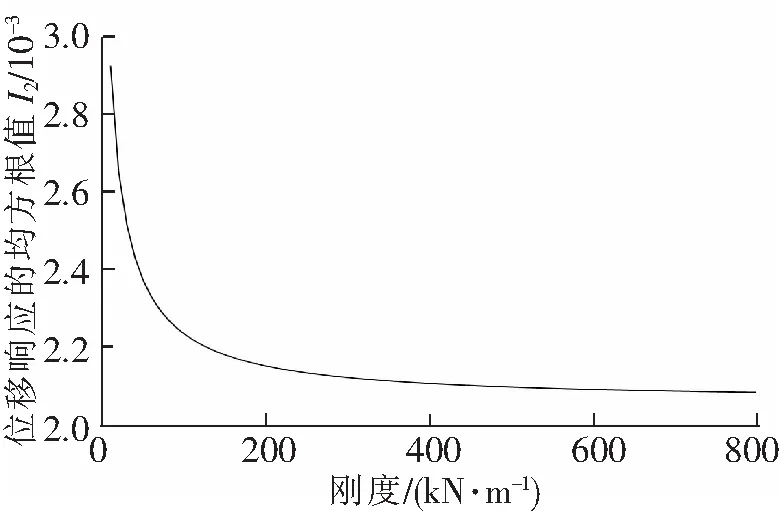
如前所述,该穿梭车可用于多种工业场合,这里以混凝土运输作业为例。普通混凝土的比重在2 000~2 800 kg/m3之间,1/4车身的质量为416.25 kg,1/4容积为0.215 m3,因此满载时车重最高达到1 018.25 kg。设计要求空载返程时速度尽可能快,并保证一定的垂向稳定性,要求满载时垂向静位移X0满足1.5 cm 根据H2优化[4]方法确定最优隔振参数。定义振幅放大因子 (5) 图3 幅频响应曲线 然而上述结果是在假设轨道垂向不平顺激励为谐波下得到,真实的轨道不平顺表现为随机激励,因而可认为穿梭车在行驶过程中频率比λ在一个范围内不断变化。H2优化是指系统在受随机激励的情况下,确定最优参数使整个幅频响应曲线与坐标轴围成的面积最小,从而车身响应的功率最小。幅频响应曲线与坐标轴围成的面积可以表示为 (6) 由于穿梭车在行驶过程中频率比在一个确定的范围内变化,因而考虑车行驶的实际情况来确定式(6)的积分上限。采用逆FFT法[5]生成美国六级轨道垂向不平顺时域信号,其功率谱密度函数为 (7) 式中,K=0.25;AV=0.033 9 cm2rad/m;Ωc=0.824 5 rad/m。 取轨道的空间波长为0.5~50 m,时域的采样间隔为Δ=0.001 s,穿梭车行驶速度为36 km/h,不平顺信号的时长为520 s,利用逆FFT法仿真生成的时域轨道垂向不平顺信号如图4(a)所示,仿真结果的功率谱密度与功率谱密度函数的解析值对比如图4(b)所示。由图4(b)可见,利用逆FFT法仿真得到的轨道垂向不平顺信号具有较高的精度。 图4 时域轨道不平顺仿真信号 如前所述,轨道不平顺为随机激励,具有多个频率成分,为确定轨道不平顺信号的频率范围,对信号进行Hilbert包络谱分析,得到结果如图5所示。由图5可见,轨道激励的频率主要在0~50 Hz之间。由满载时的最大垂向静位移要求和空载质量估算得到空载情况下的固有频率在3.5 ~5.5 Hz之间。因而穿梭车在行驶过程中频率比的范围为0<λ<14。将(0,14)作为性能指标式(6)的积分限,在不同的阻尼比ξ下对式(6)进行数值积分,可得到阻尼比ξ与性能指标I的关系曲线,如图6所示。 图5 轨道垂向不平顺信号Hilbert包络谱 图6 阻尼比与性能指标关系曲线 图7 最优阻尼比下刚度与性能指标的关系曲线 (8) 式(8)的含义为阻尼比ξ=0.201 0时刚度系数k与性能指标I的关系,利用数值积分方法可以得到k与I的关系曲线如图7所示。由图7可见,当刚度系数k<500 kN/m时,随着刚度系数与阻尼系数的增加,性能指标I急剧下降。这意味着在此区间增大刚度与阻尼能够有效地隔离轨道垂向不平顺引起车身的振动。当k>500 kN/m时,增大刚度和阻尼的隔振效果不再明显。 为验证悬架参数设计的合理性,利用数值方法计算在如图4所示的轨道垂向不平顺下车身的垂向振动响应。记时域轨道不平顺信号为S(t),车身垂向振动的微分方程可以写成 (9) (10) 图8 车身垂向振动响应 (11) 式中,n为采样点个数;x(ti)为第i个采样点的位移。 在不同的刚度下计算车身位移响应的均方根值,得到两者关系曲线如图9所示。由图9可见,在刚度系数k<500 kN/m时,增大刚度能使响应的均方根大幅度减小,即响应的功率大幅度减小。当刚度系数k>500 kN/m时,增大刚度的隔振效果不再明显。可见不同的刚度和阻尼参数对位移响应的均方根值的影响趋势与图7基本一致,验证了悬架参数的合理性。 图9 刚度对位移响应的均方根的影响 Simpack是多体动力学仿真的代表性软件之一,利用子结构建模技术和参数化建模方法能够高效建立起复杂的多体动力学模型,也是少数能够进行实时仿真的工具。利用Simpack对整车进行建模,主要考虑车身的浮沉、伸缩、横移、点头、摇头和侧滚以及4个车轮的浮沉、伸缩、横移和点头,共计22个自由度,模型如图10(a)所示。轨底坡为1/40,采用UIC60E1/S1002轮轨型面匹配,轮轨接触状态如图10(b)所示。轮轨接触采用等效弹性接触模型描述,利用Hertz弹性接触理论计算轮轨接触的法向力,利用Kalker简化算法[6]计算轮轨蠕滑力。仍利用美国六级谱生成轨道垂向不平顺和轨距不平顺。 图10 Simpack模型 采用根轨迹法计算该动力学模型在直线线路下失稳的临界速度。根轨迹法即通过计算模型中各个刚体在不同车速下的固有频率来确定穿梭车失稳的临界速度,当某个刚体对应的根轨迹的自然阻尼小于0时,说明此状态下的车已经失稳。根轨迹法计算的速度范围为 5~200 km/h,步长为5 km/h,计算结果如图11所示。图11(a)中,每条根轨迹代表模型中不同的刚体在不同车速下固有频率的变化。当根轨迹对应的自然阻尼小于0时即代表车已经失稳。考虑到设计误差和制造误差等因素,这里取安全余量0.04,即当自然阻尼小于0.04时认为车已经失稳。图11(b)为最小自然阻尼随车速的变化,从图11(b)可见,随着车速的增加,自然阻尼逐渐减小。当车速v>40 km/h时,自然阻尼小于0.04,车随之失稳。从而可以认为该穿梭车的临界速度为40 km/h,在保留一定安全余量的情况下高于设计速度,再次验证了参数设计的合理性。 图11 临界速度计算结果 (1) 研究了一种架空轨道穿梭车的垂向动力学特性,对隔振参数进行了优化。建立了1/4车模型,求解得到振幅放大因子。基于逆FFT法生成轨道垂向不平顺信号,通过对轨道不平顺信号进行频谱分析得到车辆行驶过程中位移激励的频率范围,利用H2优化方法确定了最优阻尼和最优刚度。 (2) 分别对1/4车模型和整车模型仿真,对优化参数进行了验证。定义1/4车模型位移响应的均方根为评价指标,仿真结果表明优化参数的位移响应均方根最小,验证了优化参数的合理性。基于Simpack建立了整车模型,利用根轨迹法确定了穿梭车的线性临界速度。仿真结果表明,线性临界速度高于设计速度,参数优化结果符合设计要求。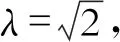

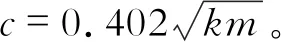


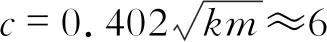
3 仿真验证
3.1 1/4车模型数值仿真
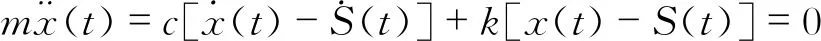
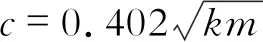

3.2 整车仿真


4 总结
