基于改进Jaccard系数的证据间相似性度量方法
2021-06-10马怀祥
董 仕,马怀祥
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
D-S证据理论是一种证据推理的数值推理方法,该理论是由Dempster首先提出,并由其学生Shafer推广并形成证据理论。D-S证据理论算法简单,融合精度高,能更有效地处理不完全、不精确信息。虽然其在不确定性推理、信息融合、故障诊断等领域有着广泛的应用,但是D-S证据理论存在的一些问题限制其进一步推广,如在合成高度冲突证据时方法失效。针对如何合成高度冲突证据这一问题,国内外学者进行了深入的研究,提出的解决方法主要分为2类,一类是修正D-S组合规则[1-2],一类是对证据源数据预处理[3-4]。在2类方法中,如何有效地度量证据体之间的冲突程度,是研究者需要考虑的至关重要的问题。
典型的度量证据间冲突程度的方法有冲突系数法、Jousselme证据距离[5]、余弦相似度[6]等。Jousselme首先将Jaccard系数应用到证据之间距离的计算之中,使得含多元素焦元的证据之间的距离度量更加明确。利用Jaccard系数衡量多元素焦元证据之间相似性的方法在文献[3]、文献[7]、文献[8]中都有所应用。一些学者根据实际问题的需要,通过改变Jaccard系数的计算方法,构建出了不同的证据间相似性度量方法。文献[9]依据焦元之间的包含关系,构造了新的Jaccard系数计算方法,获得了一种非对称的证据间相似度模型。文献[10]通过将Jaccard系数矩阵分块,合理地解决了传感器节点证据冲突的问题。
文章从证据间相似性度量的角度出发,针对在证据合成时多元素焦元与单元素焦元间存在的结果指向不确定性的差异,提出了一种改进的Jaccard系数计算方法,降低了多元素焦元在证据相似性度量时所占比重,并在此方法的基础上建立了新的证据合成方法。
1 D-S证据理论与Jousselme证据距离
1.1 Dempster组合规则
Dempster组合规则可以将来自同一识别框架下不同信息源的证据组合起来[11]。假设识别框架为Θ={θ1,θ2,…,θj,…,θN},其中,θj为识别框架中的元素,N为元素的个数。识别框架Θ的幂集中包含2N个子集,子集的数量即为该识别框架中能够产生的命题数量。m1、m2是来自于同一识别框架的2组独立的证据体,Ai、Bj分别为证据体m1、m2的焦元,其中,i,j=1,2,…,N。利用Dempster组合规则进行两证据合成的结果如下
(1)
式中,m(A)为A的基本概率赋值(basic probability assignment,BPA),m(A)的值反映了对命题A的信任程度。
(2)
式中,k为冲突系数,是度量两证据之间冲突大小的最初方法。
1.2 Jousselme证据距离
证据m1、m2为同一识别框架Θ={θ1,θ2,…,θj,…,θN}中相互独立的2组证据体,其Jousselme证据距离[5]定义为
(3)
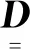
(4)
2 改进的Jaccard系数与证据合成方法
2.1 Jaccard系数矩阵的分块归一化
多元素焦元是证据中模糊性和不确定性的主要来源,在度量证据间相似性时会弱化确定性更高的单元素焦元之间的差异。相对于多元素焦元,单元素焦元具有更高的确定性,其对证据合成的最终结果影响也最大。本文从单元素焦元在度量证据间相似度时更为重要这一观点出发,在余弦相似度模型的基础上进行改进,通过将Jaccard系数矩阵分块归一化,弱化多元素焦元对相似性度量的影响,同时单元素焦元的影响度随之扩大。将Jaccard矩阵分块归一化,既可以保留单元素焦元与多元素焦元之间的集合相似关系,又可以避免复杂度越高的焦元对相似性度量的影响度越高的现象。
现有识别框架Θ={θ1,θ2,…,θj,…,θN},首先按照命题中包含识别框架元素的个数,将原Jaccard系数矩阵划分为(N-1)2+2个区域,其中将命题中包含元素最多的子集{θ1,θ2,…,θN}与空集Ø划分到一个区域。按照区域的划分进行子区域内元素的归一化处理,以达到降低复杂度高的子集在计算相似度时所占比重的目的。Jaccard系数矩阵的具体划分方式如图1所示。

图1 Jaccard系数矩阵区域划分

当i≤j时
(5)
当i>j时
(6)

(7)
2.2 改进的相似度模型
利用式(5)~式(7)中得到的新型分块归一化Jaccard系数,得到改进的相似性度量公式为
(8)
该模型是余弦相似度模型的改进,其中
(9)
‖mi‖2=〈mi,mi〉
(10)
容易证明,利用分块归一化Jaccard系数改进的相似性度量模型满足以下性质:
(1) 0≤c′(m1,m2)≤1;
(2)c′(m1,m2)=c′(m2,m1);
(3)c′(m1,m2)=1⟺m1=m2;
(4)c′(m1,m2)=0⟺(∪Ai)∩(∪Bj)=Ø。
2.3 改进的相似性度量方法的有效性分析
为了验证改进的相似性度量方法的有效性,参考文献[6]和文献[12]中的例子,将本文方法与Jousslme et al[5]所提方法、Wen et al[6]所提度量相似度的方法对比分析。文献[5]中Jousslme距离dBPA是度量2个证据体之间距离的方法,需要将Jousslme距离转化为相似性测度1-dBPA,以便于分析对比。
例1 假设识别框架为Θ={
θ1,θ2,θ3},在识别框架中共有23-1=7个非空子集,使m1{θ3}=1且一直保持不变,而使m2不断变化,m2的变化过程如下。在第一个事件发生时,m2中7个焦元的值相等且都为1/7;由第一个事件变为第二个事件时,将m2{

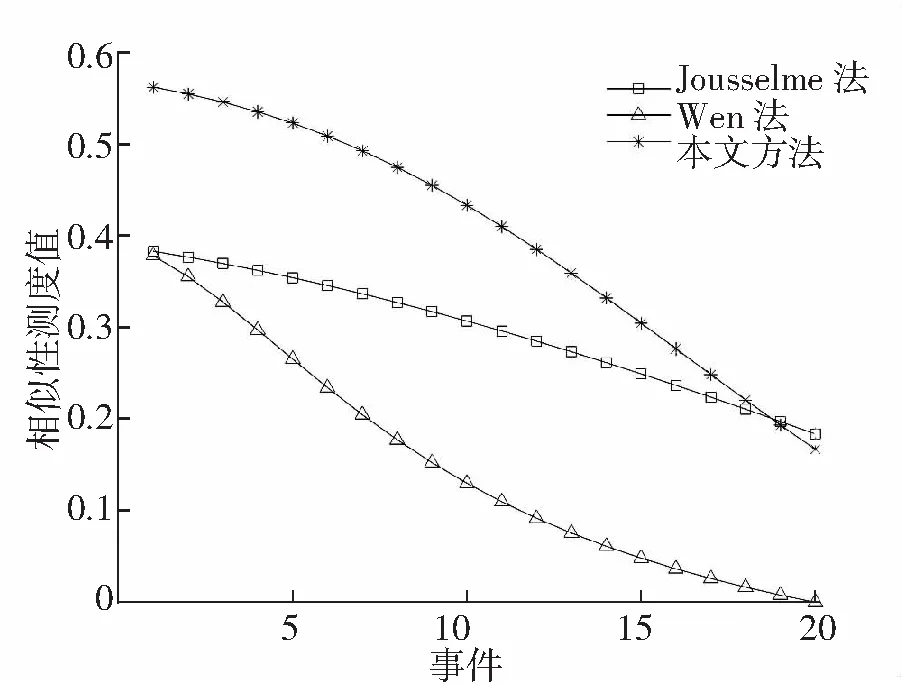
图2 3种相似性度量方法值的变化情况
对于Dempster组合规则中的冲突系数k,由于两证据之间高度冲突,因而其计算方法在本例中完全失效。从趋势上看,3种相似性度量方法值的变化趋势大致相同,说明3种度量方法均有一定的合理性。当事件20发生时,根据Wen法测得的两证据之间的相似度为零,这是因其在计算相似性时将多元素焦元视为独立的个体,忽视了两证据之间客观存在着一定的相似性。Jousselme法与本文法在例1事件的变化过程中,证据间相似度的值都呈下降趋势且不为零。本文方法相较于Jousselme法,在事件1发生时赋予了两证据之间更高的相似性;随着事件的不断变化,证据m2中的多元素焦元BPA值的占比逐渐增大,单元素焦元对应的比重逐渐减少,应用本文方法获得的两证据体之间相似度值相较于Jousselme法下降速度更快,证据之间的相似性度量更加明确。
2.4 基于改进相似性度量方法的加权证据组合
结合文献[3]中所用加权平均的方法,利用改进的相似度计算公式,对证据源数据预处理,步骤如下。
步骤1 由式(8)~式(10)分别计算n条证据之间的相似度,得到相似度矩阵CM
(11)
式中,cij′为证据mi和mj之间相似度的大小,其中,i、j=1,2,…,n。
步骤2 计算各条证据的重要度
(12)
步骤3 计算每条证据的权重
(13)
式中,crd(mi)为每条证据的权重ωi。
步骤4 依据式(13)所得的证据权重对证据源加权平均,得到修正后的数据为
(14)
最后,利用Dempster组合规则合成n-1次,得到合成结果。
3 算例分析
通过以下仿真算例,将本文方法与Dempster组合规则、Murphy[13]法以及文献[3]中所提方法对比,验证本文方法的有效性。
例2 假设识别框架为Θ={
θ1,θ2,θ3},5个相互独立的证据体的BPA为:
m1(θ1)=0.5,m1(θ2)=0.2,m1(θ3)=0.3;
m2(θ1)=0,m2(θ2)=0.9,m2(θ3)=0.1;
m3(θ1)=0.55,m3(θ2)=0.1,m3(θ1θ3)=0.35;
m4(θ1)=0.55,m4(θ2)=0.1,m4(θ1θ3)=0.35;
m5(θ1)=0.55,m5(θ2)=0.1,m5(θ1θ2θ3)=0.35。
表1中分别列举出了几种方法的合成结果。通过对表中的数据分析得知,证据体m1和m2为高度冲突数据,采用Dempster组合规则合成的结果中m(A)=0,并且当证据量进一步增加时,m(A)的值仍然为零。这是由于证据m2对命题A的支持度为零,出现了一票否决的现象,Dempster组合规则失效。文献[3]中所提方法与本文方法均是在Murphy法基础上的改进,因此在两证据合成时3种方法均出现同样的结果,随着证据量的增加,Murphy法因其是对证据源的简单平均而导致合成效果较差。
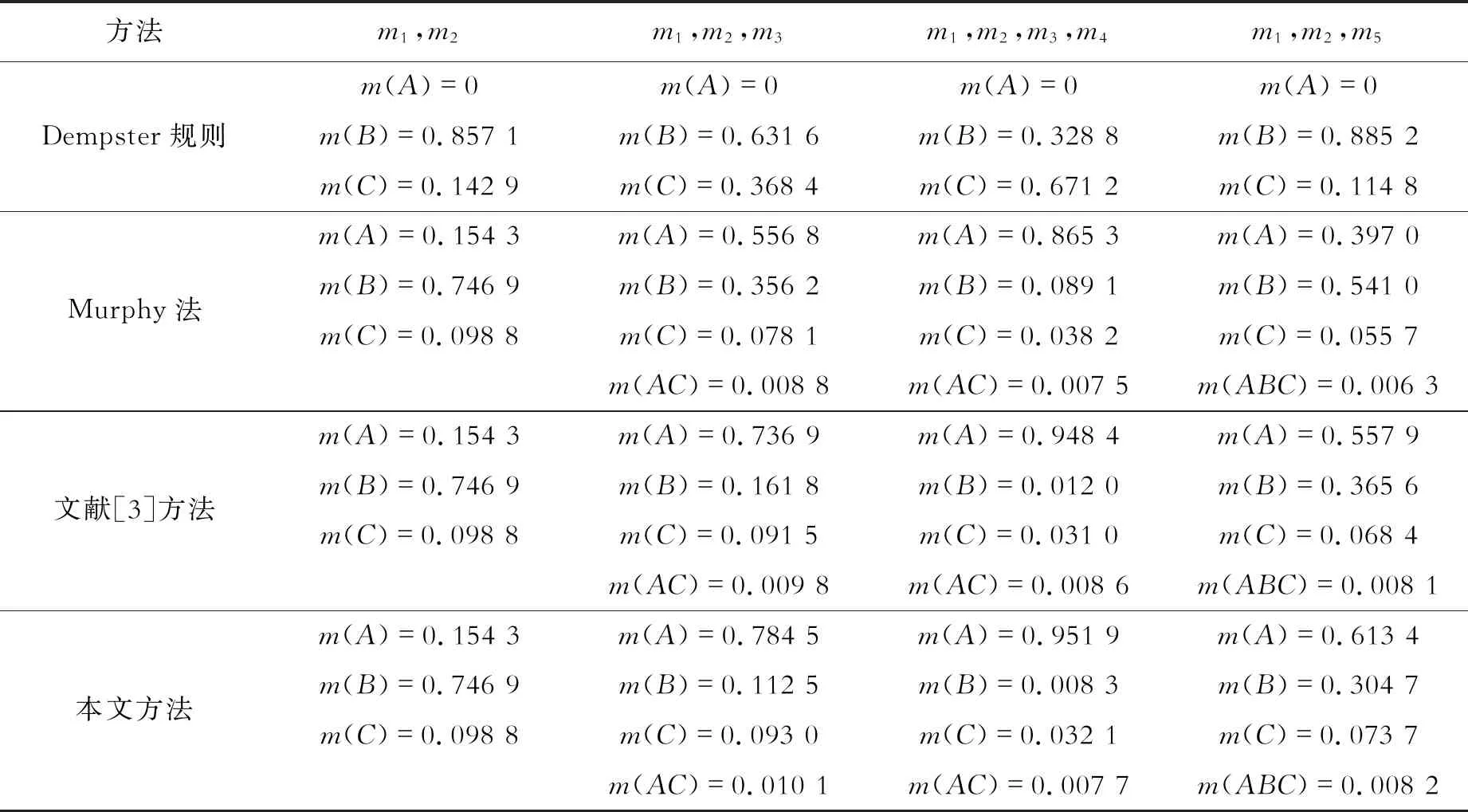
表1 不同方法合成结果比较
本文方法与文献[3]中所提方法的结果均优于Murphy法,且由于本文方法在评价证据间相似性时更多考虑了单元素之间的相似性,扩大了单元素焦元的影响力,使得单元素部分相似度更高的证据所分配的权重更高,因此增强了BPA值更大事件的支持程度。当m1、m2、m33组证据合成时,m(A)的值相较于文献[3]中所提方法提升了6.46%;随着证据量的增多并出现m1、m2、m3、m44组证据合成的情况时,本文方法的最终所得m(A)值为0.951 9,相较于Murphy法以及文献[3]方法对命题A的支持程度仍为最高;在对含有更复杂元素焦元的证据m1、m2、m53组证据合成时,本文方法相较于文献[3]中所提方法m(A)的值提升了9.95%。
4 结论
通过将Jaccard系数矩阵分块归一化,对含有多元素焦元证据体间的相似性做出了新的定义,对多元素焦元与单元素焦元在相似性度量时的重要度做出了明确划分。通过不同相似性度量方法的对比分析,本方法在对相同的事件处理时,扩大了相似度的变化范围,使证据间相似性度量更为明确。通过仿真算例表明,应用本文相似性度量方法对证据源数据预处理,合成的结果更加准确;在证据中的焦元复杂度更高时,利用本文所给相似性度量方法的合成结果相较于其他方法更为有效。
