三体船艏斜浪中扭摇运动特性预报分析

付峥， 李云波， 龚家烨， 李昂

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001； 2.上海海事大学 海洋科学与工程学院，上海 200011)

三体船是由1个舯体和2个侧体组成的高性能船型，具有良好的快速性、良好的耐波性和稳性、甲板面积大等优点[1-2]，近些年受到各国的广泛关注。自本世纪初以来，三体船实船在世界各国的军船和民船领域得到广泛的应用，各国学者对三体船水动力性能的研究也在逐步深入。

扭摇运动是由于不同自由度间运动共同作用所产生的特殊运动形式，会造成船员及乘客的强烈不舒适感，甚至会对船舶安全航行造成威胁。随着多体船的出现，扭摇运动越来越引起重视。双体船的扭摇问题已经引起了学者的关注[3]。三体船由于侧体的存在，其全船型宽较大，长宽比较小且船型复杂，已经发现有扭摇运动现象出现。但是，三体船在什么情况下发生扭摇运动，扭摇运动具有什么特征等问题目前还没有研究。理论上讲，三体船扭摇运动可能造成侧体出水、砰击等非线性运动状态，会对三体船航行的安全性产生不利影响，因此，进行三体船扭摇运动研究具有非常重要的理论和工程实际意义。

现有的船舶耐波性研究中，通常认为横向运动与纵向运动之间没有相互影响，所以在计算时会分别在2个运动方程中求解。但是考虑三体船扭摇运动时，需要考虑横摇和纵摇运动之间的相互影响和耦合作用。Nayfeh等[4]和Virgin[5]较早开始了横向和纵向耦合运动，主要通过运动方程中添加横摇、纵摇间耦合项来研究耦合运动。随后很多学者纷纷开展了横摇纵摇之间的运动耦合问题研究。研究者利用多尺度摄动方法处理了非线性耦合运动方程，唐友刚[6]、周光耀[7]、Li[8]等分别使用多尺度摄动分析方法求解多自由度运动方程，探究了船舶、海洋平台等结构物在波浪中的横摇-纵摇耦合运动问题，研究发现，这些结构物在特定波浪状态下均会出现不同自由度之间运动的耦合现象。同时，研究表明，当某一自由度的固有频率与遭遇频率一致时，会出现强烈的共振现象，运动幅度增大。当某一自由度运动增大至能量饱和状态时会出现能量转移，导致该方向运动不再增大，另一方向自由度运动响应快速增长。洪竹[9]研究表明，这种不同自由度之间的耦合运动会降低船舶在波浪中航行的稳定性，较之单自由度运动更容易造成船舶的倾覆。可见，船舶的横摇-纵摇耦合运动的研究对船舶在波浪中，尤其是斜浪中的安全航行有着非常重要的意义。

目前船舶横摇-纵摇运动耦合问题研究多基于势流理论，求解过程中存在一些基本的假设和经验公式近似，忽略流体粘性作用，阻尼力主要采用经验公式。研究表明，基于势流理论预报船舶横浪和艏斜浪中运动时，采用经验公式或近似公式会带来数值计算结果偏差；另一方面，在研究对象上，现有研究多针对常规单体船[6-7,10-11]和海洋平台[8,12]，未见有三体船横向和纵向运动耦合，以及扭摇运动研究报道。

本研究基于粘流理论，在开源软件OpenFOAM的基础上，利用通过内场不可压缩NS方程模型和外场全非线性势流理论模型匹配的Qale-FOAM求解器，对三体船艏斜浪中运动响应进行数值模拟，求解三体船升沉、纵摇、横摇运动响应及速度响应。基于非线性动力学理论和船舶动稳性理论对预报数据进行分析。在多航速下研究波陡对三体船斜浪航行时的横摇和纵摇运动幅值及运动稳定性的影响，并分析其扭摇运动特性。

1 数值预报方法

1.1 控制方程

基于OpenFOAM开源软件平台，采用外场全非线性势流波浪水池与内场CFD计算域相结合的QaleFOAM[13-14]求解器，对船舶在艏斜浪中的运动响应进行模拟。内场CFD计算域满足质量守恒方程及输运方程如下：

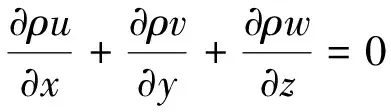
(1)

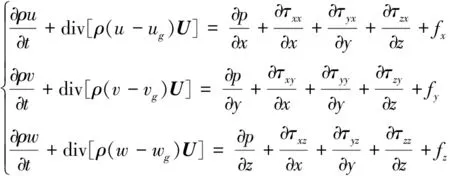
(2)

式中：ρ表示流体密度；U表示流场速度矢量；u、v、w为其3个分量，(ug,vg,wg)为流场点中的网格运动速度；p表示流场动压力；τ表示二阶偏应力张量；f表示质量力，本文中fx=fy=0，fz=ρg。

外场波浪模拟基于全非线性势流理论的QALE-FEM(quasi arbitrary Lagrangian-Euler finite element method)方法模拟二维波浪，并通过过渡域向内场CFD计算域传播，计算过程采用弱耦合的方式进行迭代计算。假设QALE-FEM中的流体为理想流体，流场速度势：

Φf=Φw+r·Uc，

式中：Φw为波浪速度势；r为流场场点位置；Uc为来流速度。

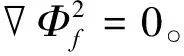
1.2 自由液面

本研究使用流体体积函数(volume of fluid，VOF)方法捕捉自由液面。VOF方法通过流体体积函数捕捉自由液面的位置，默认各项流体互相不存在穿插，并引入相体积分数，定义每个控制单元中，第q相的体积分数为：

(3)

式中：Vq代表q相在控制单元内所占体积；V是控制单元的体积；αq=0即表示该单元内没有q相流体，αq=1即表示该单元内充满第q项流体，当0<αq<1时，说明该控制单元中存在q相流体和其他流体的交接面，此时，该控制单元的输运特性可表示为：

(4)

2 运动模拟方法及验证

2.1 船舶运动模拟方法

本研究中使用水线长3 m的三体船模型进行运动响应预报，船型主尺度见下表1。

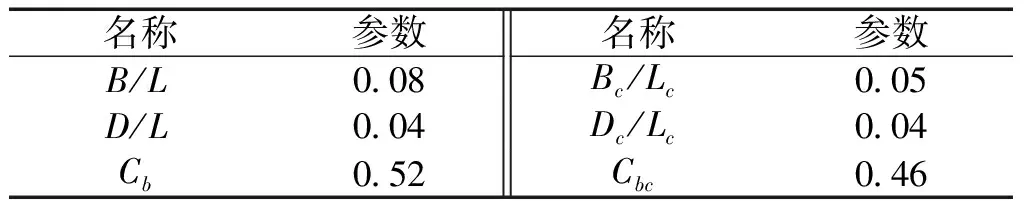
表1 船型主要参数Table 1 Main characteristic dimensions of hull forms

表中，L、B、D、Cb代表主体水线长、主体水线宽、主体吃水和主体方型系数，Lc、Bc、Dc、Cbc分别代表侧体水线长、侧体水线宽、侧体吃水和侧体的方形系数。

船舶运动模拟时，同时使用大地坐标系o-xyz和随船坐标系o-x′y′z′。随船坐标系原点与船舶重心重合，x′指向船艏，y′指向左舷，z′垂直于水平面指向上。运动初始状态下，随船坐标系与大地坐标系重合，随后与船体以相同的运动状态进行运动。

波浪传播方向沿大地坐标系ox轴负方向，船舶航行方向沿随船坐标系ox′轴正方向，二者夹角为浪向角β，本文研究工况中的艏斜浪以β=135°为基础进行理论预报，浪向角示意图见图1。

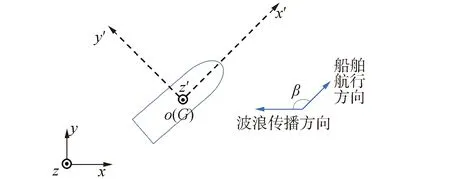
图1 浪向角Fig.1 Wave direction angle

通过2个坐标系之间转换来实现物理量的坐标变换[14-15]，船舶在水平面上的位移和垂直于水平面的升沉由局部坐标系中的速度向量和加速度向量进行表示。船舶绕不同轴的旋转角度通过欧拉角和局部坐标系下响应的角速度进行表示。欧拉角变换率表示为：

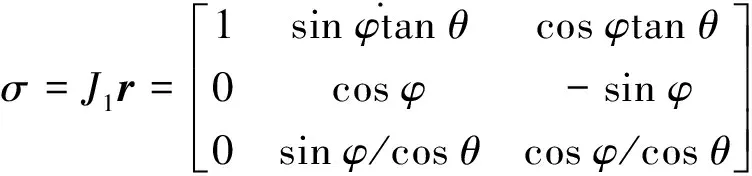
(5)

式中r=(rx,ry,rz)为局部坐标系下的角速度；φ、θ、ψ分别为船舶的横摇、纵摇、艏摇角度。

两坐标系下所受的力和力矩也需要通过转换矩阵来实现，转换矩阵J2可表示为：

(6)

内场粘流计算域示意图见上图2，计算域选取4倍船长，其中船前1倍船长，船后1.5倍船长，左侧、右侧边界距离船舶1.5倍船长，底部距离自由液面1.5倍船长，顶部距离自由液面0.5倍船长。

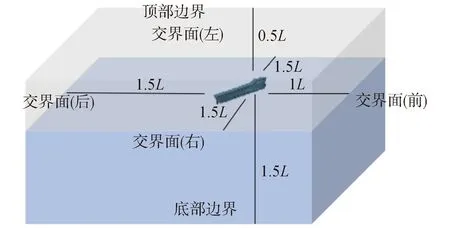
图2 波浪中运动响应NS计算域Fig.2 NS computational domain of motion in waves

在模拟船舶运动过程中，约束船舶纵荡、横荡和艏摇运动，开放并监测船舶的垂荡、横摇和纵摇自由度。约束纵荡运动用以控制船模以指定航速行驶，约束艏摇运动和横荡运动用以控制船舶航向和航行轨迹。三自由度运动模型可以更加准确的模拟指定航行工况下的船舶耦合运动状态。

使用OpenFOAM开源代码的前处理模块snappyHexMesh进行网格划分，并对船体周围网格和自由液面网格进行加密。使用有限体积法(finite volume method)对上述方程进行离散，使用PISO(pressure-implicit split-operator)算法求解压力、速度耦合方程组。进而求解三体船在斜浪下的运动方程，得到运动响应结果，并将计算结果用于横纵摇运动耦合特性分析。

2.2 波浪模拟及验证

本研究使用一阶波浪理论进行波浪模拟，选取与模拟船运动的等长计算域进行波浪模拟验证，模拟波长3.27 m, 波高0.14 m的波浪。为节约计算网格，将计算域宽度缩小至1 m。模拟得到的波高云图见图3。

图3 波高云图Fig.3 Scalar figure of wave amplitude

表2 波浪模拟的网格收敛性验证网格参数Table 2 Mesh parameters for grid independence test of wave simulation

表3 波浪模拟网格收敛性验证结果

定义3套网格所计算的相对幅值的平均结果分别为Sk1、Sk2、Sk3，则可定义收敛因子Rk为：

(7)

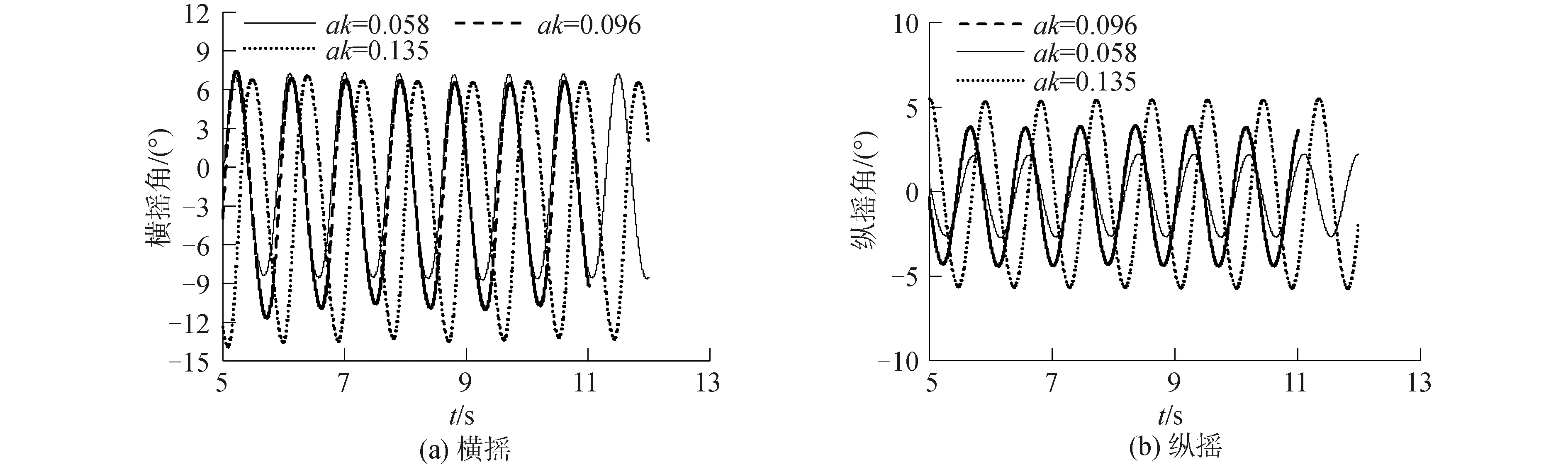
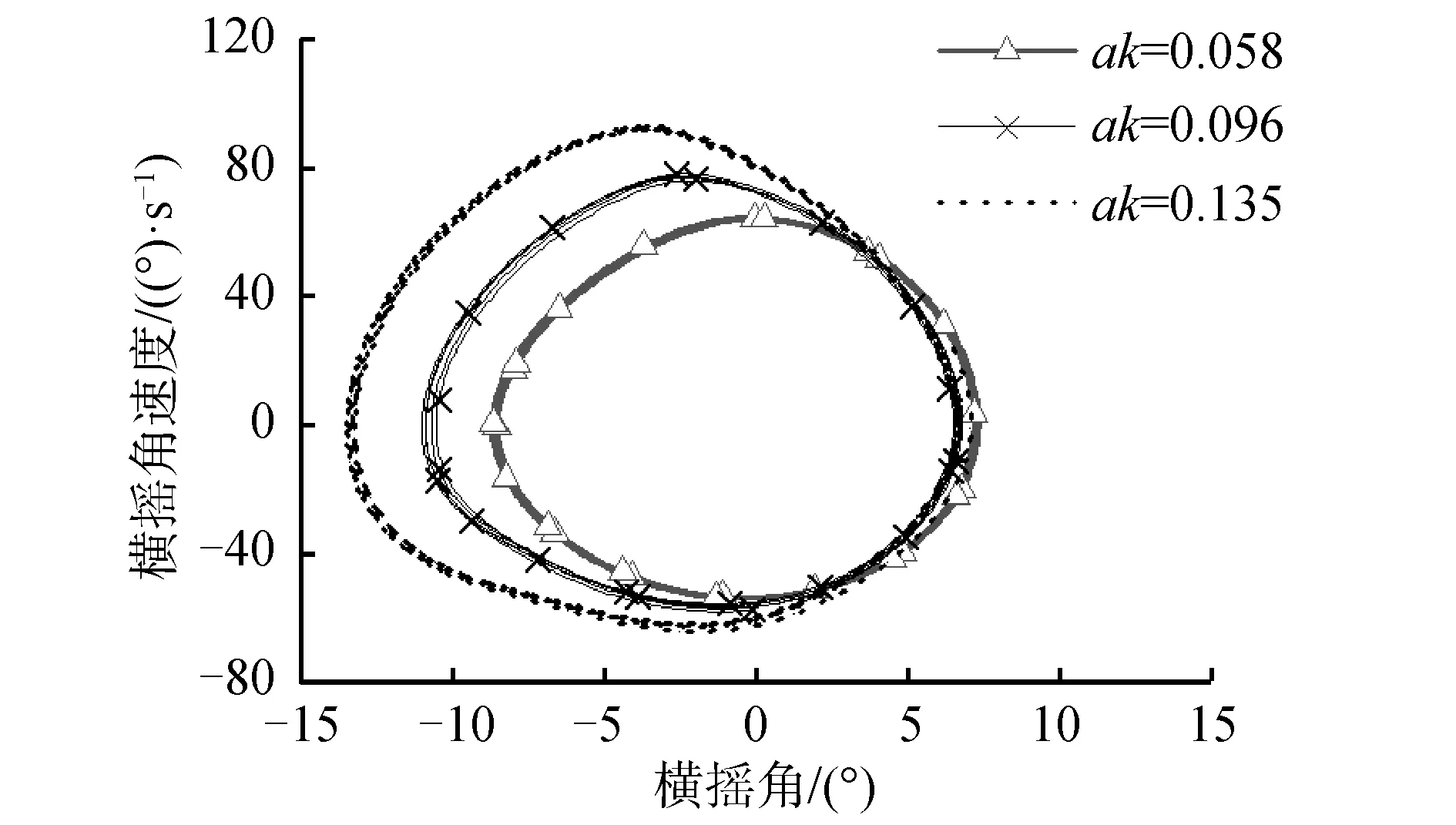
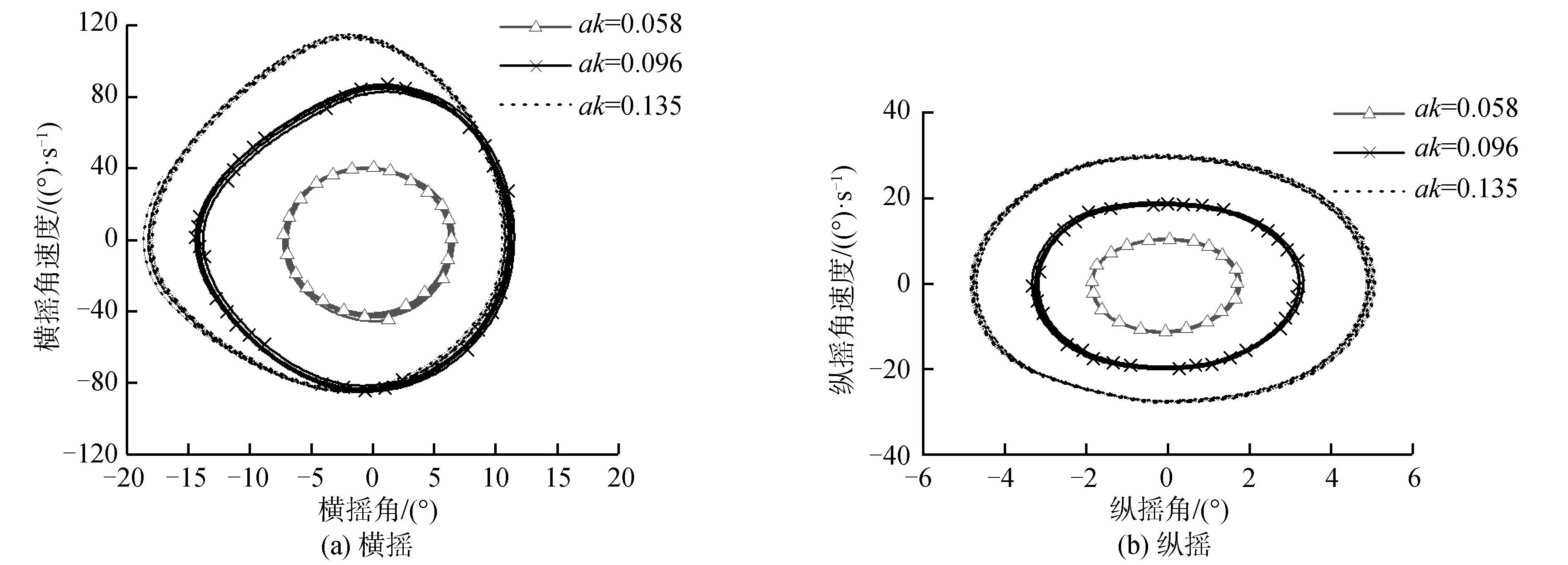
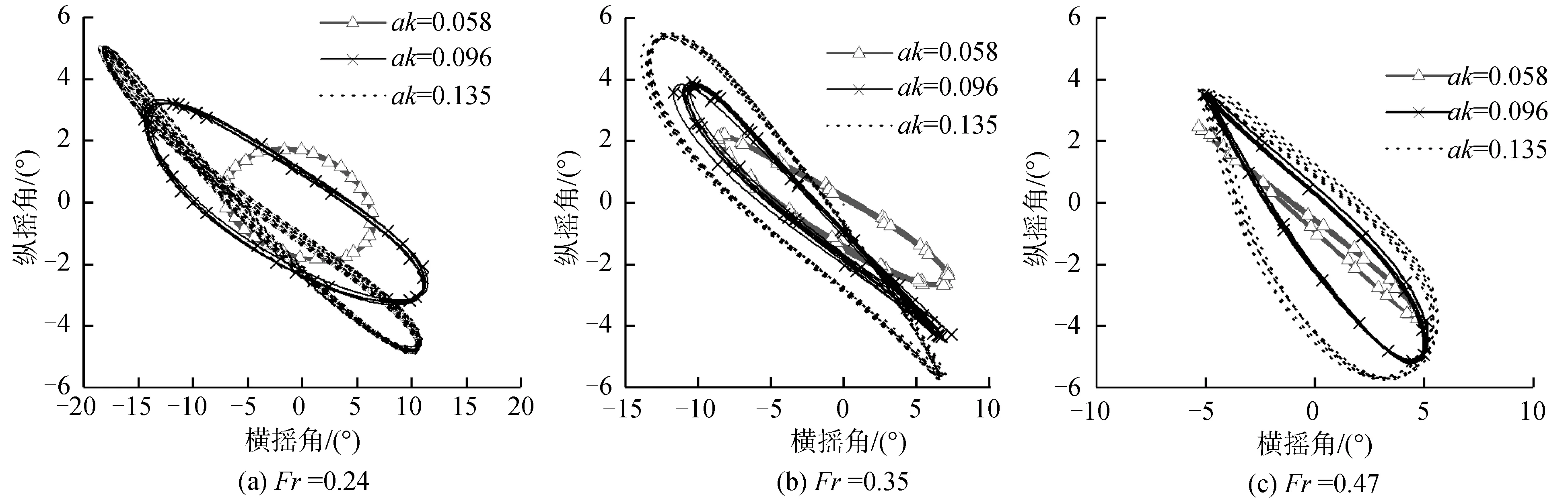
0

由表3可见，3套网格的模拟相对误差均不超过5%，网格数量最多的第1套网格(G1)尽管在计算精度方面有所提升，但预报时间相比于第2套网格(G2)的计算时间增大了4倍。综合考虑计算精度和计算时间，选取网格数量居中的第2套网格进行后续数值模拟。

3 三体船扭摇运动模拟及结果分析

数值模拟中的运动参数和波浪参数见表4。选取3个航速，3个波高，共9个工况，其中航速的选取是在设计航速Fr=0.35的基础上，选取一个较高航速(Fr=0.47)，一个较低航速(Fr=0.24)来对比不同航速下的运动的特征，在巡航航速的基础上变换航速以使研究更具普遍性，对船舶的实际航行也有更重要的意义，具体工况见表4。

表4 研究工况Table 4 Working condition of research

预报得到的三体船运动响应幅值结果见图4。

由图4可见，在不同航速下的艏斜浪运动中，横摇和纵摇运动响应均随着波陡增大而增大。当航速较低时，横摇运动幅值随波陡变化更加明显；当航速较高时，纵摇运动幅值随波陡变化更加明显。

图4 不同航速下横摇-纵摇运动响应幅值对比Fig.4 Comparison of amplitude about pitch and rolling motion with different velocity

当Fr=0.47时，波陡的增大并不会导致横摇运动的进一步增大，纵摇运动大幅度增大，增大后的纵摇幅值与横摇接近，出现了比较明显的扭摇运动，船体绕横摇纵摇矢量和扭摇运动。

3.1 不同航速下波陡对运动稳定性的影响

选取设计航速(Fr=0.35)，135°浪向角，改变波陡，数值预报得到的三体船艏斜浪中运动响应见图5，分别为横摇和纵摇运动的时历曲线。

图5 不同波陡下运动时历曲线Fig.5 Time series of different wave steepness

由图5可见，波陡增加会导致三体船在艏斜浪中的横摇和纵摇运动响应均增大，但二者的变化规律不相同。

随着波陡的增加，三体船纵摇运动时历曲线幅值增加，正负方向几乎是对称增大。整体变化仍随波陡呈线性变化，非线性不明显；但是，波陡对横摇运动的影响呈现明显的不对称性，即随着波陡的增加，正向横摇幅值并没有明显增长，负向的横摇运动幅值明显增大，变化幅值呈现出比较明显的非线性特征。ak=0.096的艏斜浪工况下横摇角可达到-10°以上，此时侧体已经完全出水，三体船已经处于强非线性横摇运动状态，见图6为当横摇运动较大时，船尾处截面的侧体出水截图。就本研究的预报结果而言，ak=0.135时，三体船仍可以正常航行，并未出现侧翻或倾覆现象，但横摇运动、纵摇运动响应均较小波陡海况有大幅度增长。

图6 三体船侧体出水Fig.6 The side hull of trimaran out of water

在非线性动力学领域，周期运动的相平面图可以直观的对运动的稳定性进行分析和判别，近些年已广泛应用到船舶的运动响应的相关研究中[7,9，18]。本研究将三体船在艏斜浪中的数值计算结果用相平面图进行判断。图7为Fr=0.35时，3个波陡下的三体船横摇运动相图。

图7 不同波陡下的横摇运动相平面Fig.7 Phase program of rolling in different wave steepness

由图7可见，小波陡的工况下，横摇运动处在相对稳定的运动状态；随着波陡的逐渐增大，横摇运动的相平面图逐渐由稳定运动向不稳定运动过渡；波陡增大到ak=0.135时，已经出现了混沌运动状态，造成了船舶不稳定运动。

当三体船在艏斜浪中低速航行时，分析Fr=0.24时的扭摇运动稳定性。图8为Fr=0.24时的横摇运动相平面图和纵摇运动相平面图。

由图8(a)可见，当三体船在低速艏斜浪航行时，横摇运动在小波陡时呈现稳定运动状态。当波陡增大，横摇角度和角速度均随之增大。但增大到ak=0.096后，横摇运动幅值只在负方向继续随波陡的增大而增大。可从运动相平面图中明显看出运动稳定性的变化，在ak=0.096之后，运动逐渐呈现不稳定状态。

图8 运动相平面(Fr=0.24)Fig.8 Phase program of motion (Fr=0.24)

由图8(b)可见，低速状态下纵摇运动随波陡的变化规律与Fr=0.35时的变化状态一致，整体随波陡的变化并不会呈现很明显的非线性增长，运动在大波陡状态下也可以保持稳定简谐运动状态。

图9为Fr=0.47时的横摇运动相平面图和纵摇运动相平面图。

由图9可见，当航速增长到Fr=0.47时，三体船运动随波陡的变化规律逐渐与低速和中速时产生了一定的变化。横摇运动幅值不再随波陡明显增长，其运动角度和角速度的变化范围均很小。纵摇运动从小波陡开始即出现负方向幅值偏大的情况，即整体运动呈现尾倾状态。当波陡ak=0.096时，纵摇仍旧保持的稳定运动状态，但当波陡ak继续增大至0.135时，纵摇运动相平面图开始出现明显的不规整现象，运动已经呈现出混沌状态。

图9 运动相平面(Fr=0.47)Fig.9 Phase program of motion (Fr=0.47)

3.2 波陡对扭摇特性的影响

为进一步探究横摇运动和纵摇运动之间的联系与影响，将两自由度运动以李萨如图形(Lissajous-figure)的形式进行分析，该方法近年被广泛应用到各大工程领域。李萨如图是由互相垂直的2个简谐振动方向所合成的规则封闭曲线[19]。在横摇、纵摇均为稳定运动时，二者即为相互垂直的简谐运动。图10为三体船在不同航速下的横摇-纵摇运动李萨如图，图中每个点均代表船舶在某一时刻的运动状态，每条曲线描述了船舶在该工况下的运动变化规律。

由图10可以看出，三体船在小波陡海况中低速航行时，横摇运动和纵摇运动之间的李萨如图形为标准的椭圆，二者均是非常规整的简谐运动。而随着航速增大、波陡增大，均会导致三体船的运动规律发生变化，摇荡运动只是周期运动，并非简谐运动。

图10 不同波陡下横摇-纵摇耦合运动李萨如图Fig.10 Lissajous-Figure of rolling-pitch coupled motion with different velocities

在低速状态下(Fr=0.24)，随着波陡的增大，船舶在艏斜浪中的横摇和纵摇运动的李萨如图形逐渐发生偏移。当波陡达到ak=0.135时，曲线出现明显的混乱现象，即在此状态下横摇和纵摇运动已不是围绕着某一矢量方向做规整摇摆，运动呈现一种非常危险的扭摇状态。

在中高航速状态下(Fr=0.35,0.47)，随着波陡的增大，船舶横摇运动和纵摇运动的李萨如图并不是规整椭圆，在其中一侧的幅值位置为椭圆弧，另一侧的幅值位置产生明显的尖端。这种现象是由上节所述的横摇运动2侧幅值不对称现象造成的，此时的横摇运动并不是规整的简谐运动，但仍呈现稳定的周期运动现象。

可见，三体船的低航速下的扭摇运动对波陡更加敏感。在低速状态下，三体船在小波陡中运动规整、稳定，在大波陡中呈现不规则运动，是非常危险的航行状态；在高速状态下，三体船在不同波陡中仍在进行稳定的周期运动，但会由于横摇的非线性运动造成扭摇运动并非规整的简谐运动，安全性比低速大波陡时较好。

4 结论

1)在不同航速下，波陡的增大都会使三体船横摇和纵摇的运动响应相应增大，但变化规律有所区别。在低速时，纵摇运动随波陡的增大呈线性增长；横摇运动随波陡的增大呈现明显的非线性，且正负方向的横摇运动增长量并不相同。在高速时，纵摇运动随波陡的增长呈现出一定的非线性，波陡达到ak=0.135时，纵摇运动已非规整运动；横摇运动则随波陡变化不再明显。

2)三体船在大波陡艏斜浪中低速航行时，三体船的耦合运动呈现明显的不稳定特征，运动状态的规则性明显变差，且主要是由于非线性横摇运动引起的，相比之下，同样的大波陡工况中提高航速可以适当降低到运动的不规则特征，使扭摇运动变得逐渐稳定。