考虑群桩效应的液化场地桩-土动力p-y曲线研究

2021-06-10惠舒清张效禹唐亮崔杰满孝峰凌贤长

哈尔滨工程大学学报 2021年6期

惠舒清，张效禹，唐亮，崔杰，满孝峰，凌贤长,3

(1.哈尔滨工业大学土木工程学院，黑龙江哈尔滨 150090； 2.广州大学土木工程学院，广东广州 510006； 3.青岛理工大学土木工程学院，山东青岛 266033)

历次震害调查表明[1]，强震下场地液化是导致桩基桥梁结构震害的重要原因。因此，国际上对强震下液化场地桩基桥梁抗震问题十分关注，并陆续开展了卓有成效的研究[2-3]。工程实践与研究表明[4-5]，可液化场地条件下，桩基桥梁结构地震反应分析的关键在于精确模拟桩-土动力相互作用。现有桩-土动力相互作用分析方法中，p-y曲线法具有无需选取土体本构模型、计算参数容易获取、计算时长很短等特点，在工程设计中得到广泛使用。

现阶段，已有多位学者提出了用于桩-土相互作用分析的p-y曲线，如Reese等[6]提出了砂土的p-y曲线、Matlock等[7]提出了水下软粘土和硬粘土的p-y曲线、Lombardi等[8]提出了土体液化后的p-y曲线。然而，现有关于砂土p-y曲线的研究多是针对单桩展开的，其对群桩基础是否适用尚需进一步探讨。为此，本文针对液化场地群桩-土-结构耦合体系地震反应离心机振动台试验，建立了可靠的三维有限元数值模型；随后，在反复的数值模拟与分析基础上，构建了考虑桩间距效应的液化场地群桩-土动力相互作用p-y曲线，并通过离心机试验结果对其正确性进行了检验。

1 液化场地桥梁群桩-土地震相互作用离心机试验数值模拟

1.1 离心机试验简介

本文针对Wilson[4]开展的液化场地桥梁群桩-土地震相互作用离心机试验进行数值模拟工作，离心加速度为30g，文中给出的参数均为按照离心加速度确定的原型尺寸，试验布置见图1。试验中，地基土采用内华达砂(Nevada sand)，总厚度20.5 m，分为上、下两层。上层为相对密度约35%～40%的饱和松砂，厚度为9.1 m。下层为相对密度约80%的饱和密砂，厚度为11.4 m。水位线位于地表处。试验采用真空砂雨法制备地基模型土。试验中，基础为2×2群桩基础，其中，桩采用铝制管桩，桩长14.5 m，桩径0.67 m，壁厚19 mm，桩间距2.67 m(约为4倍桩径)，弹性模量70 GPa，屈服应力290 MPa，屈服弯矩5.3×103kN·m。承台尺寸为长×宽×高：4.6 m×4.6 m×2.3 m；柱墩高10.9 m。上部结构(即模型顶部质量块)配重2 000 kN。试验以1995年日本Kobe地震中的地震记录作为基底激励，如图2所示。

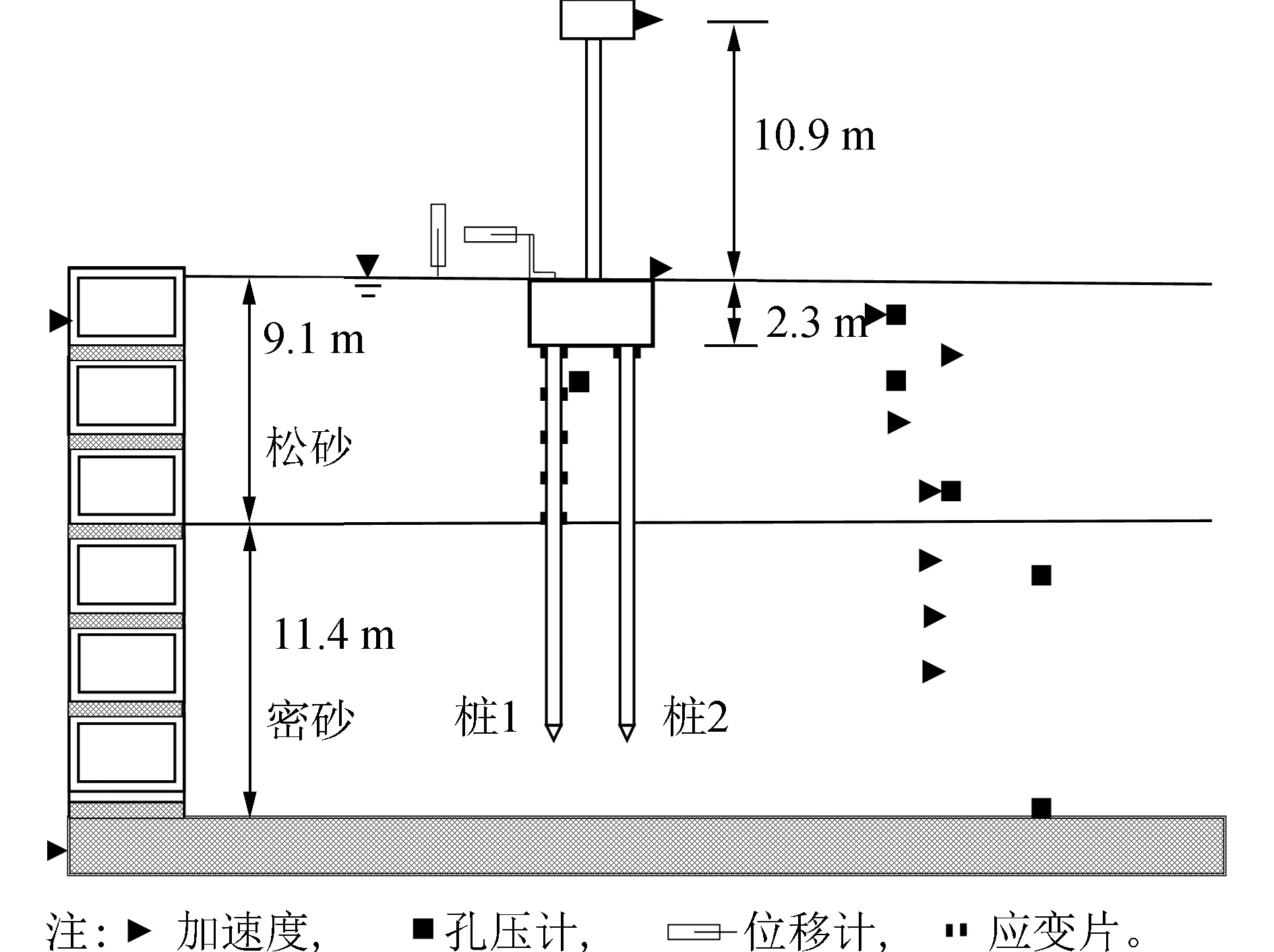
图1 离心机试验Fig.1 Centrifuge test setup

图2 模型输入地震动Fig.2 Base input motion

1.2 数值模型

本文数值模拟借助有限元计算平台OpenSees完成。针对上述离心机试验，考虑到试验体的对称性，对称建立了液化场地群桩-土-上部结构动力相互作用三维有限元数值模型(图3)，模型长×宽×高：51 m×10.5 m×20.5 m。

图3 有限元模型Fig.3 Finite element model

模型中，饱和砂土选用土-水完全耦合的六面体单元模拟。该单元是基于Biot动力方程，将饱和砂土模拟为液固两相介质。单元本质上仍为20节点六面体等参数单元(即为20-8节点单元)，其中，角上的节点包括1个孔压自由度和3个位移自由度，棱上节点只含3个位移自由度。

砂土本构模型采用Elgamal等[9]提出的多屈服面弹塑性本构模型。该本构模型能够准确地模拟砂土的液化动力特性。在多屈服面弹塑性本构模型理论框架下，模型采用数量可自定的圆锥形屈服面。这些屈服面通过定义不同的切向剪切模量，表示不同的土体应力-应变关系。此外，通过定义加载-卸载流动法则，该模型可以有效地模拟砂土的剪胀效应。该本构模型已通过离心机试验结果进行了大量验证，具体详见文献[9]。砂土本构模型参数采用Lu等[10]给出的本构模型建议值，见表1。

表1 砂土的参数Table 1 Model parameters for sand

选用线弹性的梁-柱单元模拟。桩和柱墩材性计算参数与试验中桩和柱墩的物理特性参数保持一致。桩的尺寸效应，通过在桩单元与土单元直接布置刚度极大的杆单元实现(即刚性连接)，见图4，其中，杆单元的抗弯刚度设置为桩的10 000倍[13]。桩-土之间接触面的模拟，借鉴Rahmani和Pak提出的方法[3, 11]，通过在桩-土之间设置零厚度单元实现，如图4所示。为了提高计算的稳定性与收敛性，模拟承台仍然采用20-8节点六面体实体单元模拟。不过，计算中约束了其节点上孔压自由度。上部结构通过在柱墩顶端节点施加集中质量实现模拟。

图4 桩-土相互作用模拟Fig.4 Modeling of soil-pile interaction

模型中，将基底和侧面设置为不透水边界，保证在该面内孔隙水流速为零[13]。地表处定义为自由面，保证水位线处孔压为零。侧面边界选用OpenSees中的Shear beam边界。该边界可以实现位于同一高度上与振动方向垂直的2个侧面边界产生的水平向位移保持一致，模拟试验中层状剪切土箱的土体剪切[14](图1)。

1.3 数值模型可靠性验证

图5～图7对比了离心机试验和数值计算的自由场土体的超孔压和加速度时程、上部结构加速度时程、承台加速度和桩的弯矩时程。

图5 超孔压试验值与计算值对比Fig.5 Comparison of the experimental and computed results of excess pore pressure

可以看出，试验和计算获得的孔压吻合很好。计算得到的2.9 m埋深处土体在2～4 s内加速度幅值略大于试验值，但总体上土体加速度峰值的试验值与计算值相差不大。震动开始时，上部结构加速度的试验值与计算值吻合度较低，但幅值相差不大；相比而言，震动后期上部结构加速度的试验值与计算值吻合度较高。在2～4 s和6～8 s时段内，承台加速度试验值与计算值的幅值整体变化趋势稍有差异，但均在合理范围内。桩1弯矩时程的计算值与试验值吻合较好，说明该模型可以很好地反应液化场地桩的动力响应规律。

图6 加速度试验值与计算值对比Fig.6 Comparison of the experimental and computed results of acceleration

图7 弯矩试验值与计算值对比Fig.7 Comparison of the experimental and computed results of bending moment

如上所述，虽然各响应的试验值与计算值在某个时间段可能存在一定的差异性，但是总体上计算和试验得到的曲线吻合很高，能够较真实地重现离心机试验中群桩和上部结构的动力响应基本规律与典型特征。

2 群桩-土动力相互作用p-y曲线

用于描述桩-土相互作用的p-y曲线中，土反力用p表示，相对位移用y表示。目前，静力条件下砂土p-y曲线的研究已经比较成熟，特别是API(american petroleum institute)规范中建议的砂土p-y曲线已广泛应用。但是，动力作用下液化砂土的p-y曲线的研究还不够成熟，且现有p-y曲线的研究均未考虑群桩效应。群桩效应是指群桩基础承受荷载后，由于承台、桩、土的相互作用使其桩侧阻力、桩端阻力、沉降等性状发生变化而与单桩明显不同，承载力往往不等于各单桩承载力之和这一现象。鉴于此，本节在上述群桩数值模型的基础上，进行液化场地群桩-土地震相互作用p-y曲线的研究。

2.1 p乘因子法的局限性

API规范中建议的砂土p-y曲线已被广泛应用于工程设计。目前，关于液化砂土p-y曲线的研究，以Boulanger等[12]提出的“p-乘因子法”(p-multiplier)应用最为广泛。该方法以API规范中未考虑土体液化效应的砂土p-y曲线为基础，通过对土反力p进行折减来考虑土体的液化效应。

为了研究“p-乘因子法”在液化场地群桩-土动力相互作用分析中的适用性，根据唐亮[13]的研究结果，需要对比“p-乘因子法”提出的p-y曲线与有限元计算得到的动力p-y曲线骨干线的区别。按照唐亮[13]建议的方法，通过拟合不同幅值下动力p-y曲线滞回圈的顶点，可以获得其动力p-y曲线的骨干线，这里分别探讨土体液化前后“p-乘子法”的有效性。

在上述有限元模型基础上，选取幅值0.10g、0.15g、0.20g、0.25g、0.30g、0.35g、0.40g和0.50g的正弦波对模型进行激励。图8(a)给出了孔压比为0.3时的动力p-y曲线骨干线绘制过程，即基于计算得到的动力p-y曲线滞回圈，确定其滞回圈顶点，拟合各个顶点得到其骨干线。图8(b)对比了埋深5.7 m处有限元计算得到的动力p-y曲线和“p-乘因子法”提出的p-y曲线的区别，发现两者整体趋势基本相同。但是“p-乘因子法”的土反力稍大于数值计算结果。

图8 动力p-y曲线骨干线Fig.8 Backbone curves of dynamic p-y

图9为土体孔压比为0.6和0.9时的对比情况，发现其规律与孔压比为0.3时的相同，即两者变化趋势相近。但是，“p-乘因子法”计算得到的土反力偏大。因此，“p-乘因子法”可以描述液化前群桩-土相互作用p-y曲线的基本形式，但仍需对其土反力大小做进一步修正。需要说明的是，其他孔压比及不同埋深处的动力p-y曲线具有相同的规律，这里不再一一列出。图10对比了液化后土体动力p-y曲线与“p-乘因子法”提出的p-y曲线，发现两者相差较大。液化后的土体动力p-y曲线骨干线呈现上“凹”形式，这是不排水条件下，循环荷载作用时饱和砂土发生的剪胀现象导致，然而“p-乘因子法”提出的p-y曲线并未考虑这一特征。综上所述，“p-乘因子法”并不能准确描述液化场地群桩-土地震相互作用p-y曲线特征。鉴于此，本文将基于精细化的有限元计算模型，改进“p-乘因子法”现有局限性，提出更精确的液化场地群桩-土地震相互作用p-y曲线。

图9 p-乘因子法与动力p-y曲线对比Fig.9 Comparison between p-multiplier and dynamic p-y curve

图10 p-乘因子法与液化后土体动力p-y曲线对比Fig.10 Comparison between p-multiplier and dynamic p-y curve for the liquefied soil

2.2 改进的p-y曲线

1)土体液化前p-y曲线的修正。

上述研究表明，“p-乘因子法”能够描述液化前群桩-土相互作用动力p-y曲线骨干线的基本形式，但其土反力值偏大。究其原因在于，该法并不是直接针对群桩基础提出的，同时未考虑桩间距效应的影响。为此，基于验证的群桩-土地震相互作用分析的三维有限元模型，以桩间距和桩径的比值(s/d)为控制指标，对“p-乘因子法”构建的p-y曲线进行修正。

图11为不同桩间距下(s/d分别等于3～8)计算得到动力p-y曲线与“p-乘因子法”中的p-y曲线的对比。同时，针对“p-乘因子法”中土反力偏大的问题，分别选取不同的桩间距修正系数m对其进行修正。

图11 不同桩间距下改进的p-y曲线Fig.11 Improved p-y curves under the different pile spaces

由图可知，修正后的p-y曲线与计算得到的动力p-y曲线滞回圈顶点位置吻合较好。此外，随着桩间距逐渐增大，修正系数m逐渐减小。当s/d=8时，不需要采取任何修正，“p-乘因子法”也能够很好地刻画计算得到的动力p-y曲线滞回圈顶点位置。换言之，当桩间距大于8倍桩径后，“p-乘因子法”能够直接用于液化场地群桩-土动力相互作用分析中。对于桩间距小于8倍桩径的情况，图12给出了桩间距与修正系数的关系，可见两者之间存在较好的线性相关性。因此，拟合得到修正系数m的计算公式：

图12 修正系数m与桩间距的关系Fig.12 Relationship between correction coefficient m and pile space

(1)

式中：m为桩间距修正系数(s/d≤7)，s/d≥8时，取m=1；s为桩间距，m；d为桩径，m。

据此，基于“p-乘因子法”，结合式(1)，得到了考虑桩间距效应的土体液化前p-y曲线表达式：

p=mmppAPI=m(1-0.9ru)A×

(2)

式中：m为桩间距修正系数(m≤7)，m≥8时，取m=1；mp为孔压修正系数；ru为孔压比；pAPI为API公式中的土反力p。

2) 土体液化后p-y曲线的修正。

研究发现，液化后土体动力p-y曲线骨干线呈现出一种“上凹”的形式。因此，为得到液化后土体p-y曲线的表达式，可选用指数函数形式对计算得到的动力p-y曲线滞回圈顶点进行拟合，即液化后土体p-y曲线的统一表达式为：

p=AyB

(3)

式中：p为土反力；y为桩-土相对位移；A、B为曲线形状控制参数。

以埋深5.7 m处为例，如图13所示，通过液化后土体动力p-y曲线滞回圈顶点拟合得到其p-y曲线的表达式：

图13 埋深5.7 m处液化后土体动力p-y曲线Fig.13 Dynamic p-y curve for the liquefied soil at 5.7 m depth

p=1.081y1.01

(4)

埋深5.7 m处的p-y曲线的曲线形状控制系数A和B的值分别为1.08和1.01。其他埋深处的曲线形状控制参数如表2所示。

为了得到便于推广使用的液化后土体p-y曲线计算公式，基于表2中曲线形状控制系数A、B和土体埋深之间的关系，拟合得到系数A和B的计算公式：

表2 不同埋深处p-y曲线形状系数A和B

A=-0.01z2+0.17z+0.36

(5)

B=0.02z2-0.35z+2.56

(6)

式中：z为土体埋深，m；A为曲线形状控制参数；B为曲线形状控制参数。

通过以上分析，最终建立一组可描述液化后桩-土动力相互作用特性的p-y曲线，该曲线主要由深度决定，可依据式(4)～(6)联合计算获得。

2.3 改进的p-y曲线正确性检验

Boulanger等[14]基于文克尔地基梁假设和离心机试验结果，提出了能够考虑桩-土分离与滑动的力学模型，较为全面地刻画地震作用下桩-土地震相互作用的物理过程。但是，该模型采用的是API规范推荐的p-y曲线，未考虑群桩效应的影响。本文将提出的改进后的p-y曲线，融入到Boulanger等[14]提出的文克尔地基梁模型中，进行改进后的p-y曲线的正确性检验。

针对上述离心机试验，基于文克尔地基梁法，建立如图14所示的液化场地群桩-土地震相互作用分析模型。模型中，桩和柱墩采用线性梁-柱单元模拟，桩和柱墩的力学参数和几何参数与试验体保持一致。考虑承台具有较大的抗弯刚度，不易破坏。因此，选用刚性连接模拟承台，其抗弯刚度与试验体保持一致。上部桥梁结构通过在柱墩顶端节点施加集中质量进行模拟。桩-土相互作用通过Boulanger等[14]提出的文克尔地基梁模型模拟，其p-y曲线采用本文提出的改进后的p-y曲线。自由场土体的孔压和位移时程借助软件Cyclic 1D进行计算。

图14 数值模型Fig.14 Numerical modeling

图15和图16分别验证了上部结构加速度和桩1峰值弯矩计算结果的正确性，图中明显看到计算值和试验值吻合较好。因此，采用本文提出的改进后的p-y曲线可以较为精确的描述地震荷载作用下群桩-土-上部结构体系的动力响应。同时，相对有限元法，简化分析方法避免了土体本构模型的选取问题，且计算时间短、计算参数也容易确定。