三元件“惯容-弹簧”反共振隔振器隔振特性分析
2021-06-10张赣波赵耀张晓东
张赣波, 赵耀, 张晓东
(1.华中科技大学 船舶与海洋工程学院,湖北 武汉 430074; 2.海军工程大学 舰船与海洋学院,湖北 武汉 430033)
在机械振动系统中,质量(或惯量)元件是一个单端点元件,而弹簧和阻尼都是双端点元件。在“力-电流”第二类机电相似理论的统一框架下,机械振动系统也必然存在一种具有2个独立、自由端点的,与电气系统的电容严格相似的元件。具有这一性质的元件被定义为“惯容”[1]。目前已经探索出机械、液压、液力、机电等类型的惯容结构[2-4]。
惯容结构的实现为超越传统的质量、弹簧和阻尼3大振动元件的串并联组合约束关系创造可行性。基于“弹簧-阻尼”并联结构的传统隔振器存在低频和线谱隔振的技术瓶颈,这是弹簧元件“通低频、阻高频”的动力特性所决定的[5]。而惯容具有“通高频、阻低频”的特性,与弹簧元件并联组合可以构建具有反共振特性的反共振隔振器[6-8]。以往关于惯容与弹簧的组合关系研究主要集中在这一并联结构上。文献[9]分析惯容对振动系统固有频率的影响,理论推导证明在隔振器结构中并联惯容降低原振动系统的固有频率。文献[10]针对“惯容-弹簧”单级并联结构反共振隔振器的隔振特性进行分析。文献[11]在“惯容-弹簧”单级并联结构基础上串联第二级弹簧,可以改善原隔振器的隔振性能。
在“惯容-弹簧-阻尼”体系下构建反共振隔振器结构,应关注解决两方面的问题:1)反共振隔振器结构的完备性,除“惯容-弹簧”并联结构外,还存在串联或混联结构;2)线谱和宽带隔振相统一,应在保持传统隔振器宽带隔振性能基础上融合线谱隔振,而不是顾此失彼。本文基于“力-电流”第二类机电相似关系,类比电气系统中“电感-电容”谐振发生条件,完备地构建出3型“惯容-弹簧”反共振隔振器基本型结构,包括1型二元件“惯容-弹簧”并联结构和2型三元件“惯容-弹簧”混联结构。重点针对三元件“惯容-弹簧”反共振隔振器,从固有频率、反共振、阻尼影响等方面分析其振动特性和隔振性能。根据力传递函数存在固定点的特征,采用动力调谐优化方法进行隔振器动力参数匹配,推导出优化动力参数计算式,并在最优状态下讨论动力参数对隔振性能的影响规律,以指导实际设计。所构建的2型三元件“惯容-弹簧”反共振隔振器结构,为寻求在被动系统上进行线谱和宽带一体化隔振提供一种有效技术途径。
1 “惯容-弹簧”反共振隔振器结构
将两端点的惯容代替单端点的质量,机械系统与电气系统完全严格相似。根据“力-电流”机电相似理论,机械系统的惯容、弹簧、阻尼分别与电气系统的电容、电感、电阻相对应。在电气系统中,电容和电感有串联谐振和并联谐振两种类型。由此推知,机械系统的惯容和弹簧也必然存在串联和并联两种谐振类型,如图1中Ⅰ、Ⅱ所示“b1//k1”、“b1-k1”,这里以“//”、“-”分别表示并联和串联关系(下同)。但惯容不具有弹簧的承载能力,一旦超过工作行程将发生类似电容的“击穿”现象[3],故在“惯容-弹簧”串联结构中必须再并联-保护弹簧,保护弹簧的位置有2种选择,一是单独与惯容并联,二是与惯容和弹簧整体并联,共2种排列方式,见图1中Ⅱ1、Ⅱ2。因此,单惯容反共振隔振器共有3型结构。
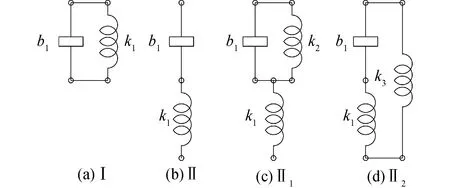
图1 反共振隔振器结构Fig.1 Architecture of anti-resonant isolator
上述3型反共振隔振器的固有频率分别是:
(1)
(2)
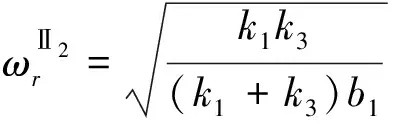
(3)
隔振器Ⅱ1的固有频率与弹簧k1无关,隔振器Ⅱ2的固有频率决定于弹簧k1、k3的合成刚度。
以反共振隔振器进行隔振系统设计,力传递率以阻抗表示为:
(4)
式中Zm、Zi、Zf分别为振源、隔振器和基础的阻抗。
式(4)表明,隔振系统的反共振特性决定于隔振器阻抗。由于隔振器的固有频率是阻抗特征方程的根,故隔振器的固有频率对应于隔振系统的反共振频率。
2 反共振隔振系统固有频率
在隔振器结构中引入惯容,使得隔振系统发生惯性耦合。隔振器Ⅰ中只有1个弹簧,而隔振器Ⅱ1、Ⅱ2中都有2个弹簧,但前者串联,后者并联,不同弹簧数量和组合关系也就决定隔振系统具有不同的固有振动特性。在刚性基础条件下,将振源看作刚体,其质量为m,记隔振器Ⅰ、Ⅱ1、Ⅱ2对应的隔振系统分别为隔振系统Ⅰ、Ⅱ1、Ⅱ2。
2.1 隔振系统Ⅰ
隔振系统Ⅰ的特征方程为:
-mω2-b1ω2+k1=0
(5)
令u=b1/m,γ=ω/ωr,求解得隔振系统Ⅰ的无量纲固有频率为:
(6)
显然,隔振系统Ⅰ的固有频率小于隔振器Ⅰ的固有频率。质量比u越大,两固有频率越接近。
2.2 隔振系统Ⅱ1
令λ=k2/k1,代入前述定义无量纲量,整理得无量纲特征方程为:
(7)
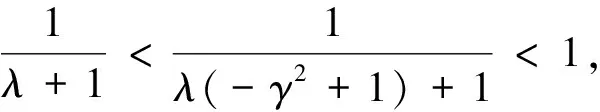
(8)
式(8)表明,第1阶固有频率的上限值决定于质量比u,并且第1阶固有频率小于反共振频率,即第1阶共振峰出现在反共振峰之前。
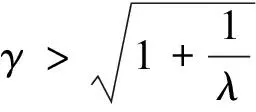
(9)
(10)
式(9)、(10)表明,第2阶固有频率的下限值主要决定于刚度比λ。显然,第2阶固有频率大于反共振频率,即第2阶共振峰出现在反共振峰之后。
2.3 隔振系统Ⅱ2
令λ=k3/k1,代入前述定义无量纲量,整理得无量纲特征方程:
(11)
观察式(11)和式(7),2方程形式相同,仅质量比系数有所区别。在隔振器Ⅱ1、Ⅱ2三元件相同的条件下,隔振系统Ⅱ2相对于隔振系统Ⅱ1的等效质量比是u(λ+1)2。由此推知,隔振系统Ⅱ2的第1、2阶固有频率也是关于质量比u的增函数,并且大于隔振系统 Ⅱ1的同阶固有频率。由于质量比u和刚度比λ存在耦合,隔振系统 Ⅱ2的第1、2阶固有频率关于刚度比λ的变化规律不同于隔振系统 Ⅱ1。
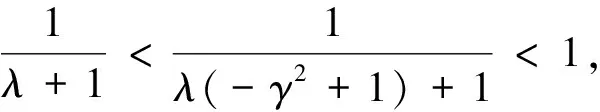
(12)
式(12)显示,隔振系统Ⅱ2的第1阶固有频率是关于刚度比λ的增函数,不同于隔振系统Ⅱ1的减函数。
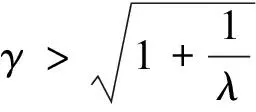
(13)
(14)
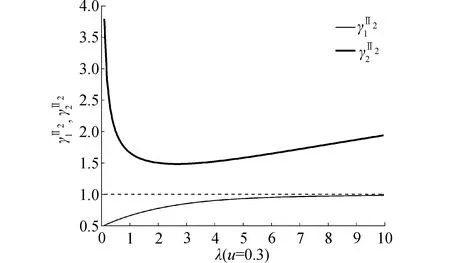
图关于刚度比λ的变化曲线Fig.2 Curves of with respect to λ
3 反共振隔振系统隔振特性
3.1 反共振隔振特性
以力传递率作为表征隔振特性的特征量,隔振系统Ⅰ、Ⅱ1、Ⅱ2的无量纲力传递曲线如图3所示。为与传统隔振器比较,一并绘制出无惯容的传统隔振系统的力传递曲线。
从图3看出,隔振系统Ⅰ、Ⅱ1、Ⅱ2都存在传统隔振系统不具有的反共振现象,在反共振频率处,隔振系统具有极低的力传递率。当激励频率等于隔振器固有频率时,隔振系统将发生反共振,激振力被大幅度隔离。这一反共振特性适用于线谱隔振。在反共振频率之后,隔振器结构Ⅰ、Ⅱ1、Ⅱ2的力传递特性表现出较明显的差异性。隔振器Ⅰ在反共振频率之后的力传递曲线上扬,逐渐接近一渐近值,而隔振器Ⅱ1、Ⅱ2的力传递曲线在第2阶共振峰后以一定速率衰减,衰减速率与传统隔振器相当,具有宽带隔振特性。
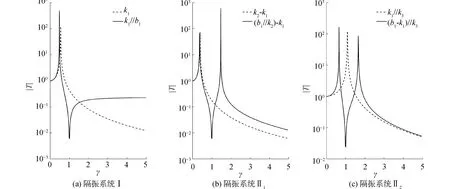
图3 隔振系统Ⅰ、Ⅱ1、Ⅱ2的力传递曲线(u=0.3,λ=1)Fig.3 Force transmissibility curves of vibration isolation system Ⅰ,Ⅱ1,Ⅱ2(u=0.3,λ=1)
隔振器Ⅰ的反共振特性仅适用于线谱隔振,如同传统隔振器,隔振性能都仅有单一性。而隔振器Ⅱ1、Ⅱ2的反共振特性表现出的隔振性能具有双重性,在保有传统隔振器宽带隔振性能的同时,集成线谱隔振性能,实现线谱和宽带一体化隔振。工程上纯线谱激励的激振源较少,在性质上大都是离散和连续的混合激励,隔振器 Ⅱ1、Ⅱ2满足工程应用要求。
3.2 阻尼影响
因未考虑阻尼,上述力传递率曲线共振峰和反共振峰都呈现尖锐、狭窄的特征。在隔振器Ⅱ1、Ⅱ2三元件基本型结构中增加阻尼元件,其位置有3种选择,如图4所示,包括c1、c2、c3、c1c2、c1c3、c2c3、c1c2c3共7种排列方式。因此,反共振隔振器Ⅱ1、Ⅱ2共有14种工程可行的拓扑结构。
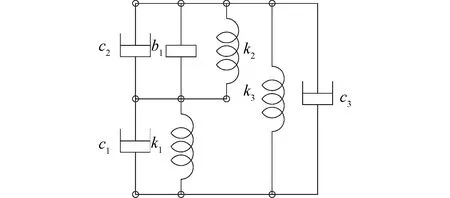
图4 阻尼排列方式Fig.4 Arrangement of damping
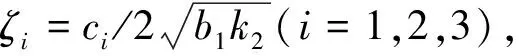
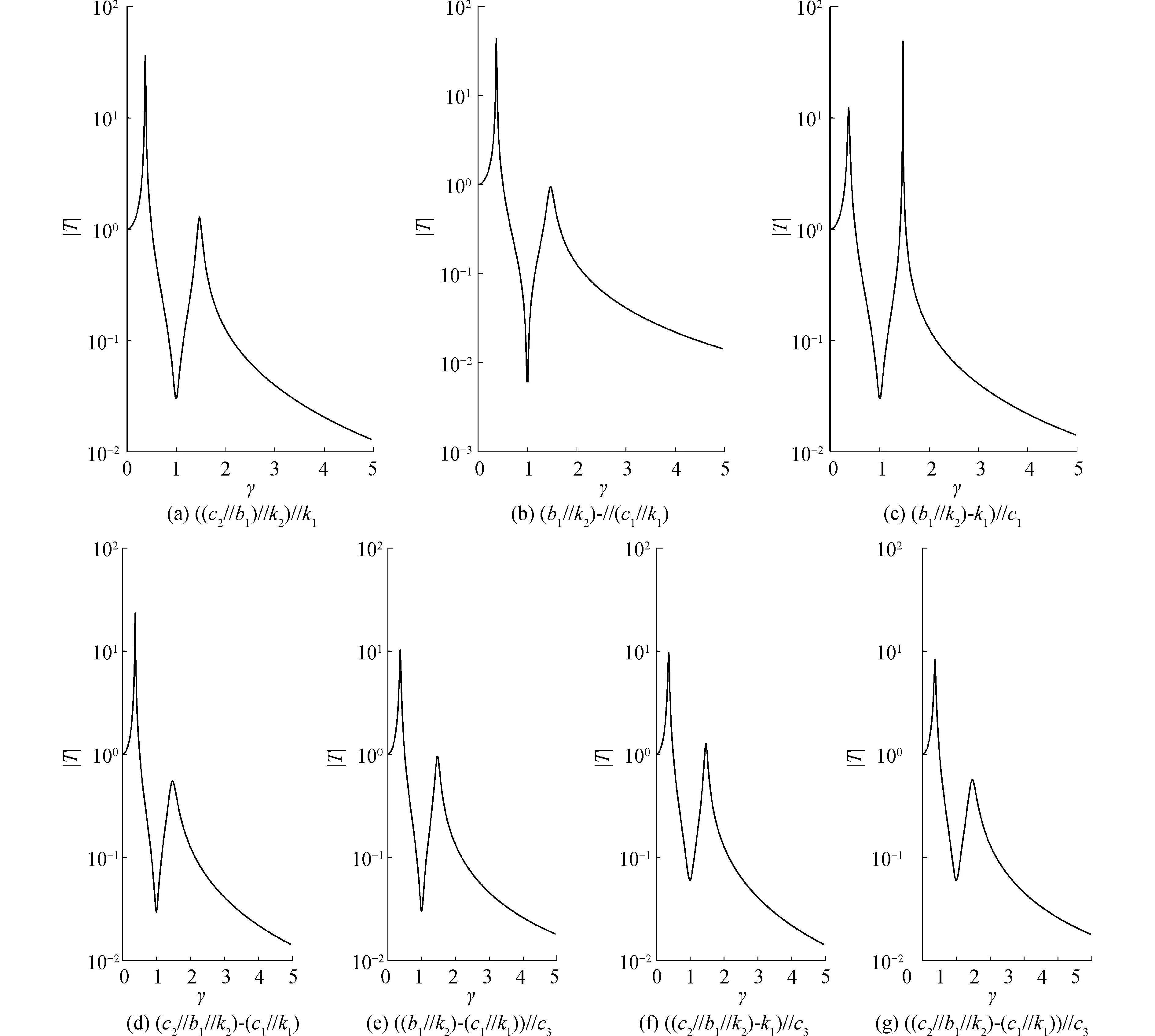
图5 隔振器Ⅱ1不同阻尼排列方式对应的力传递曲线(u=0.3,λ=1,ζi=5%)Fig.5 Force transmissibility curves of isolator Ⅱ1 corresponding to different arrangement of damping(u=0.3,λ=1,ζi=5%)
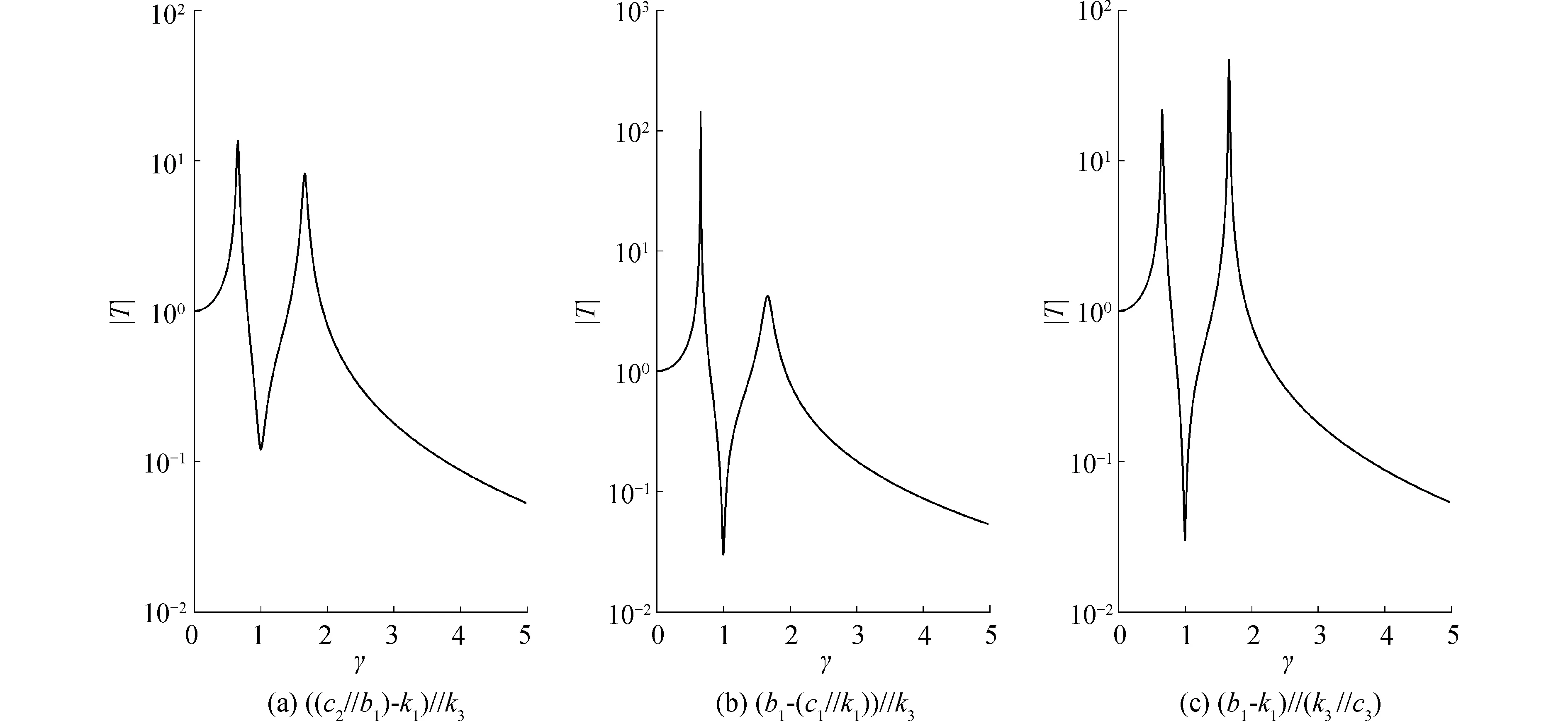
对于隔振器Ⅱ1,阻尼c1、c2、c3都存在主影响区。综合而言,阻尼c1是局部阻尼,仅控制第2阶共振峰值,相应地也控制第2阶共振峰之后的力传递率幅值,影响宽带隔振效果;阻尼c3是区域阻尼,控制第1阶共振峰值和反共振峰值;阻尼c2是全局阻尼,对第1、2阶共振峰值和反共振峰值都有控制作用,主要影响线谱隔振效果。
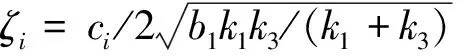
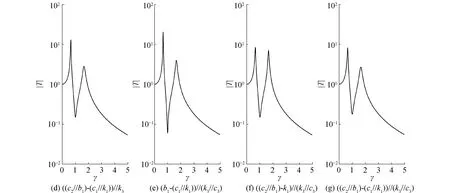
图6 隔振器Ⅱ2不同阻尼排列方式对应的力传递曲线(u=0.3,λ=1,ζi=5%)Fig.6 Force transmissibility curves of isolator Ⅱ2 corresponding to different arrangement of damping(u=0.3,λ=1,ζi=5%)
以上分析结果表明,不同位置阻尼对力传递曲线峰值的影响是相对解耦的。这为满足不同隔振要求提供有效的调节途径,如以线谱隔振为主要目标,应减小或不设阻尼c2,同时增大阻尼c1,以改善整体隔振效果。
3.3 参数优化
由于阻尼c2是全局阻尼,在隔振器Ⅱ1、Ⅱ2三元件基础型结构中引入阻尼c2,根据前述所定义的无量纲量,推导出隔振系统Ⅱ1、Ⅱ2的无量纲力传递函数分别为:
(15)
(16)
观察式(15)、(16),根据动力调谐优化理论,隔振系统Ⅱ1、Ⅱ2的力传递函数都存在不随阻尼比ζ2变化的两固定点。基于两固定点对隔振系统Ⅱ1、Ⅱ2的动力参数进行优化设计,基本步骤是:
1)寻求最优刚度比λopt,使两固定点幅值相等;
2)寻求最优阻尼比ζ2opt,使两固定点为最大值点。
以质量比u为自变量,计算得到隔振系统Ⅱ1、Ⅱ2的最优刚度比分别为:
(17)
(18)
最优阻尼比的解析解推导较繁复,采用最小二乘法拟合得到其数值解为:
(19)
(20)
在最优状态下,隔振系统Ⅱ1、Ⅱ2的力传递函数关于质量比u的曲线簇如图7所示。比较看出,隔振系统Ⅱ1、Ⅱ2力传递曲线共振峰值和反共振峰值关于质量比u的变化规律相反。隔振系统Ⅱ1与质量比u负相关,提高隔振效果应减小质量比u,而隔振系统Ⅱ2与质量比u正相关,增大质量比u可改善隔振效果。
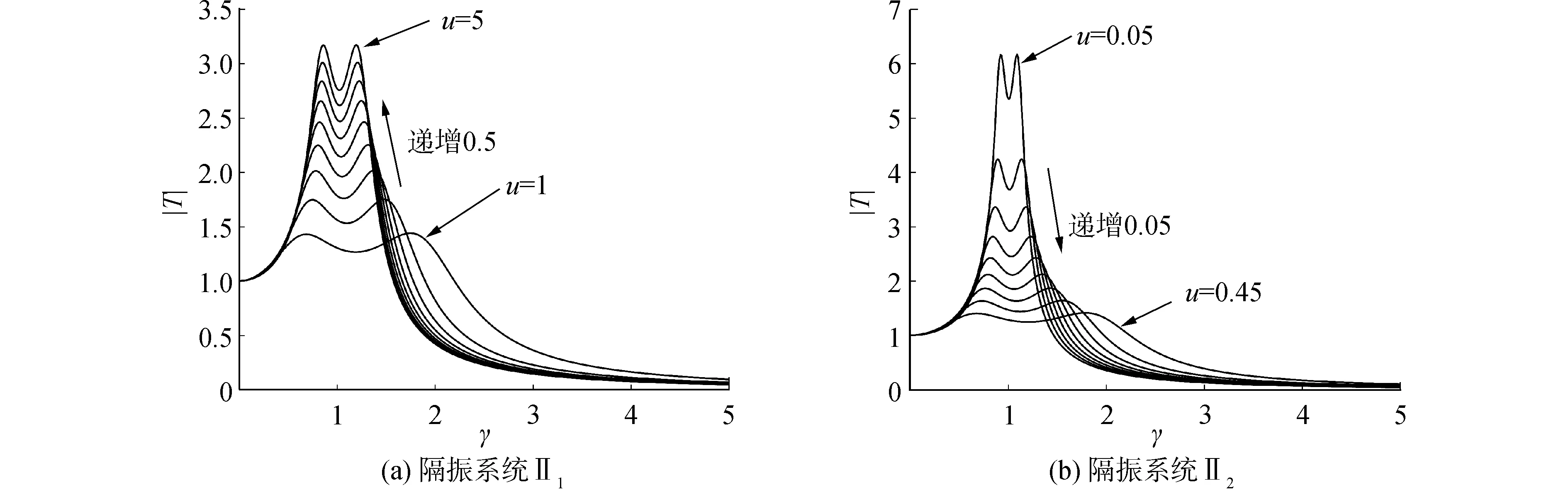
图7 隔振系统Ⅱ1、Ⅱ2的力传递曲线簇Fig.7 Force transmissibility curves of vibration isolation system Ⅱ1, Ⅱ2
反共振峰值表征隔振效果,而共振峰值间距则反映隔振效果的稳定性。对于隔振系统Ⅱ1,减小质量比u在降低反共振峰值的同时也增大共振峰值间距。而对于隔振系统Ⅱ2,增大质量比u,既降低反共振峰值,也增大共振峰值间距。因此,质量比u对隔振性能有决定性作用。
4 结论
1)“惯容-弹簧”串、并联组合可构建3型反共振隔振器基本型结构,其中,1型二元件并联结构和2型三元件混联结构,反共振频率对应于隔振器固有频率;
2)三元件“惯容-弹簧”反共振隔振器同时具有线谱和宽带隔振性能,在基本型结构中匹配增加阻尼元件可针对共振峰值和反共振峰值实施独立控制;
3)质量比是三元件“惯容-弹簧”反共振隔振器进行隔振设计的关键参数,最优刚度比和最优阻尼比都是关于质量比的函数,对隔振性能有决定性作用。
