钢筋与波纹管约束灌浆料的粘结-滑移本构关系试验研究

柳家为， 王浩， 沙奔， 郜辉， 徐寅飞， 朱克宏

(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 210096；2.中铁二十四局集团有限公司， 上海 200071)

灌浆金属波纹管连接是将预制墩柱的外露钢筋插入预埋在承台或盖梁内的金属波纹管中，并通过灌注高强无收缩灌浆料形成锚固连接。该连接方式施工方便且成本较低，目前被广泛应用于装配式桥梁结构。

钢筋与灌浆料之间力的传递是通过两者之间的粘结力来实现的，因此，钢筋与灌浆料间的粘结滑移行为是研究灌浆金属波纹管钢筋连接力学性能的核心问题之一。国内外学者针对钢筋与混凝土的粘结滑移问题已开展了大量有价值的研究工作[1-7]。Mirza等[1]和徐有邻等[2]通过开展中心拔出试验，研究了荷载等级、混凝土保护层厚度、混凝土强度和配箍率等因素对钢筋与混凝土间粘结滑移关系的影响。Ergun等[3]基于拉拔试验，研究了混凝土强度、钢筋等级和钢筋直径等因素对不同温度作用后钢筋与混凝土间粘结强度的影响，并建立了粘结强度退化模型。Oh等[4]和蒋德稳等[5]通过开展重复荷载试验，建立了随加载次数和应力水平变化的粘结本构关系模型。杨海峰等[6]和Ma等[7]通过采用加速通电锈蚀以及钢筋开槽内贴应变片等方法，研究了钢筋锈蚀对粘结强度和粘结应力分布的影响。但对于钢筋与灌浆料的粘结滑移问题研究目前尚不多见[8]。灌浆料与混凝土的材料性能存在差异，且准确的粘结-滑移本构关系是灌浆金属波纹管钢筋连接力学性能分析的理论基础，为此有必要开展钢筋与波纹管约束灌浆料间的粘结-滑移本构关系的研究。

为探究钢筋与波纹管约束灌浆料间的粘结-滑移本构关系及其影响因素，本文设计并制作了15组基准试件和5组钢筋开槽试件(每组2个)，通过中心拉拔试验，分析了不同锚固长度la和孔径比D/d(波纹管外径D与钢筋直径d比值)对钢筋与波纹管约束灌浆料间粘结滑移变化规律及粘结应力分布规律的影响，并建立了考虑锚固长度la和孔径比D/d等因素的粘结-滑移关系式。

1 试验概况

1.1 试件及材料力学性能

参照《混凝土结构试验方法标准》[9]，本试验设置基准试件和钢筋开槽试件的长度分别为10d和15d，截面尺寸均为250 mm×250 mm。试件锚固钢筋采用直径d为18 mm和25 mm的HRB400型钢筋，金属波纹管壁厚为2 mm，外径D分别为63、76和89 mm。在钢筋开槽试件的锚固长度范围内，每隔30 mm粘贴1个应变片，上下交错布置，合拢后应变片间距为15 mm。其中直径为25 mm的钢筋应变片布置如图1所示。采用环氧树脂将两半开槽钢筋密封合拢，并在加载端附近进行点焊处理，以保证钢筋受力的整体性。为避免加载过程中混凝土开裂对试验结果产生影响，于试件内设置φ8@40的横向箍筋。在试件加载端处截取PVC套管包裹钢筋，模拟无粘结段lw，并用填充材料封闭锚固钢筋和套管两端的空隙，防止灌浆料渗入[10]。锚固钢筋和金属波纹管保证严格对中，加载端钢筋预留300 mm，自由端预留20 mm，试件浇筑成型后养护至28 d。试件的具体形式见图2，试件的主要参数见表1。表1中，试件编号由3项数字组成，分别表示钢筋直径、波纹管外径和锚固长度，其中K表示试件的钢筋开槽内贴应变片。如试件18-89-03表示钢筋直径为18 mm，波纹管外径为89 mm，锚固长度为3d。

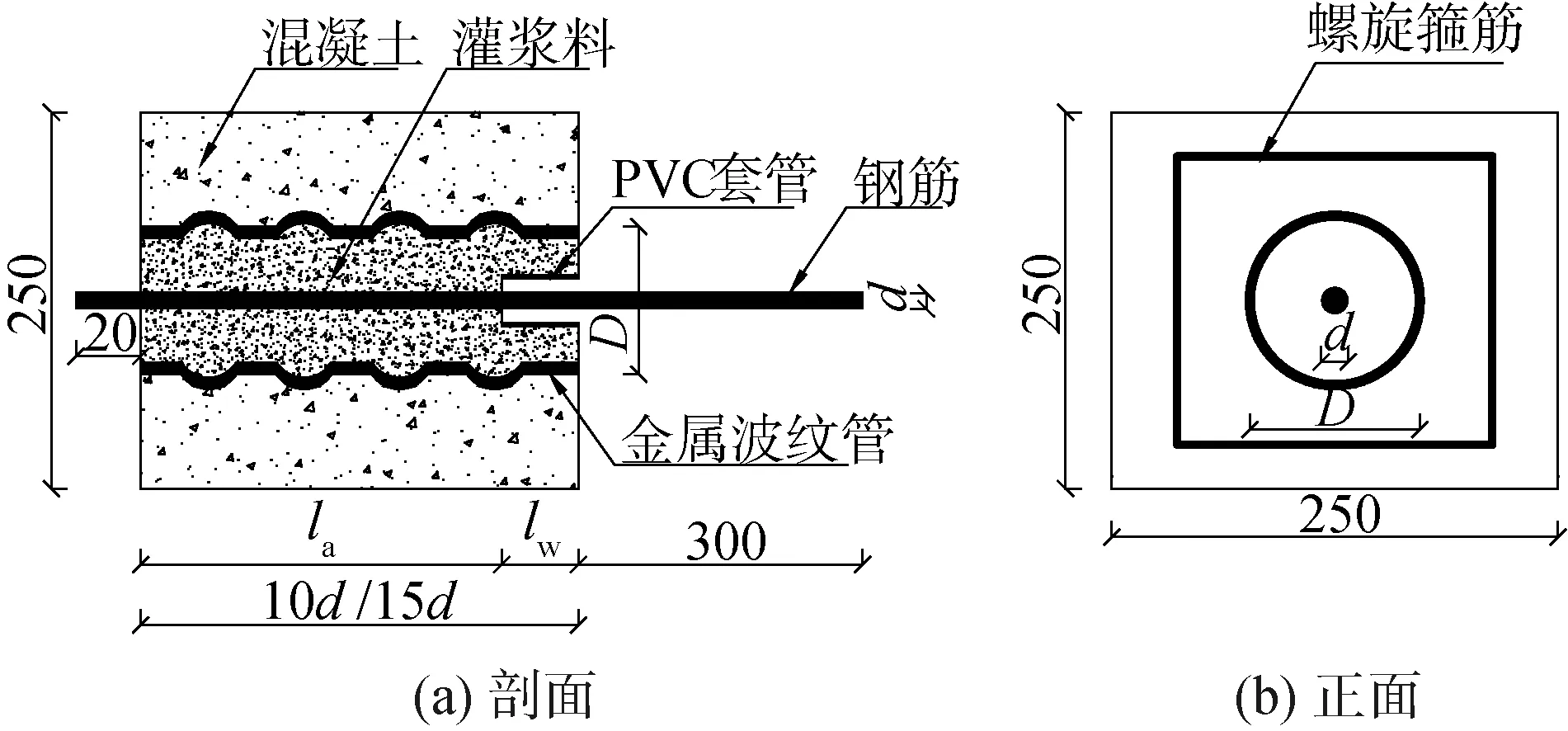
图2 试件几何形式Fig.2 Geometry of specimens

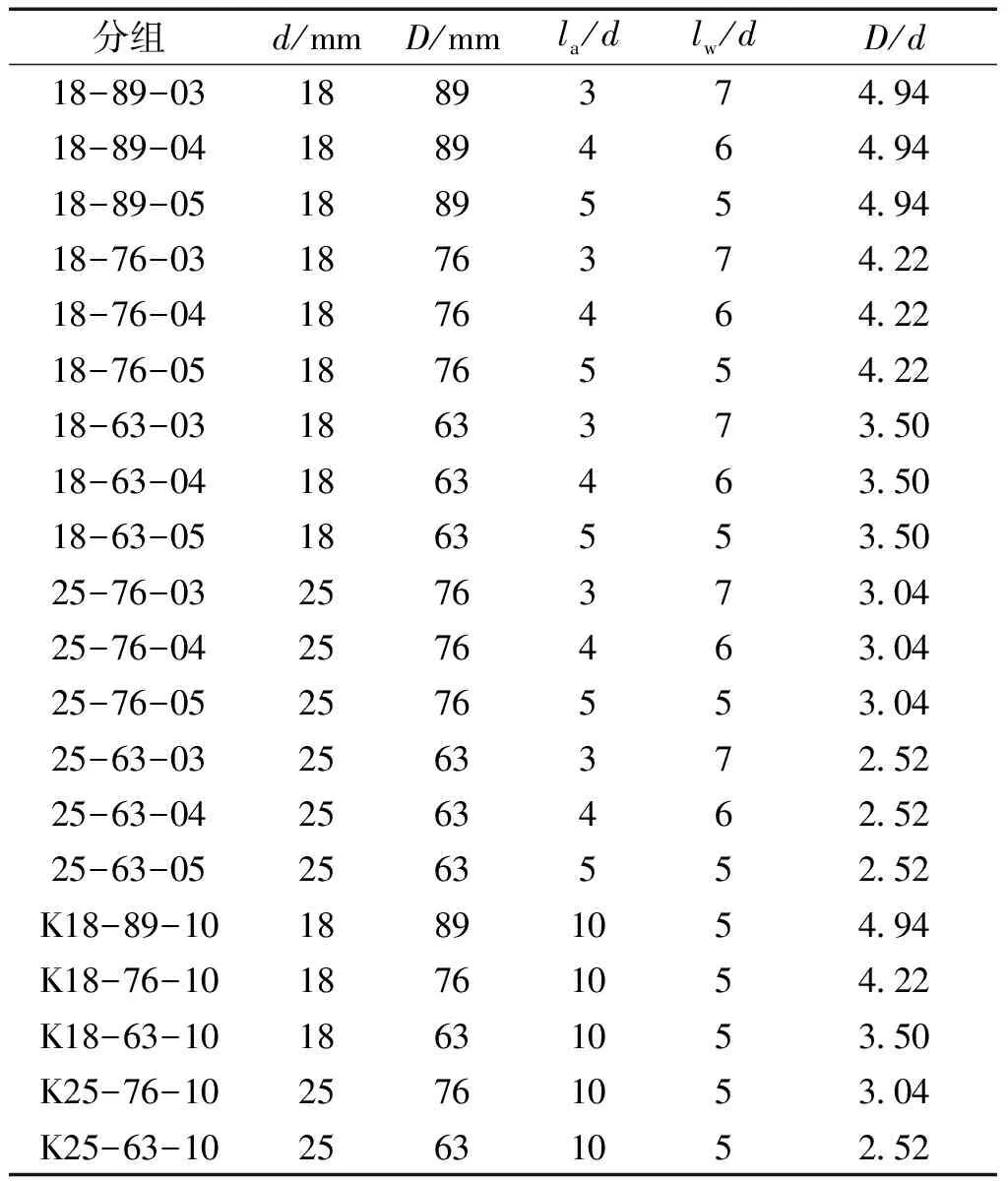
表1 试件主要参数Table 1 Main parameters of specimens

依据《水泥胶砂强度检验方法》和《普通混凝土力学性能试验方法标准》，测得3个40 mm×40 mm×160 mm灌浆料棱柱体标准试块抗压强度平均值fc为69.8 MPa，3个100 mm×100 mm×100 mm灌浆料立方体试块劈裂抗拉强度平均值ft为5.31 MPa。依据《金属材料室温拉伸实验方法》，对每组3个钢筋试件进行拉伸试验，测得钢筋的力学性能参数见表2。

表2 钢筋力学性能参数Table 2 Mechanical property parameters of reinforcement

1.2 加载装置及量测方案

试验采用30 T电液伺服式万能试验机以200 N/s的加载速率进行连续加载[9]，试验加载装置见图3。对基准试件加载至发生钢筋滑移破坏，对钢筋开槽试件加载至钢筋屈服。试验过程中，在钢筋的自由端设置1个位移计，取其滑移测量值s1为A点滑移量sA，在加载端附近C点处设置一个钢引板，将左右2个位移计置于其上，可获得滑移测量值s2、s3，并取其均值(s2+s3)/2为C点滑移量sC，则B点滑移量为sB=sC-ΔBC(注：ΔBC为BC段钢筋弹性伸长量)。钢筋与灌浆料间的滑移量采用A、B点滑移量的平均值，则平均滑移量sa=(sA+sB)/2。加载端的拉力由万能机测出，且控制位移、应变和拉力同频同时采集，以确保测量值一一对应，真实反应试件受力状态。

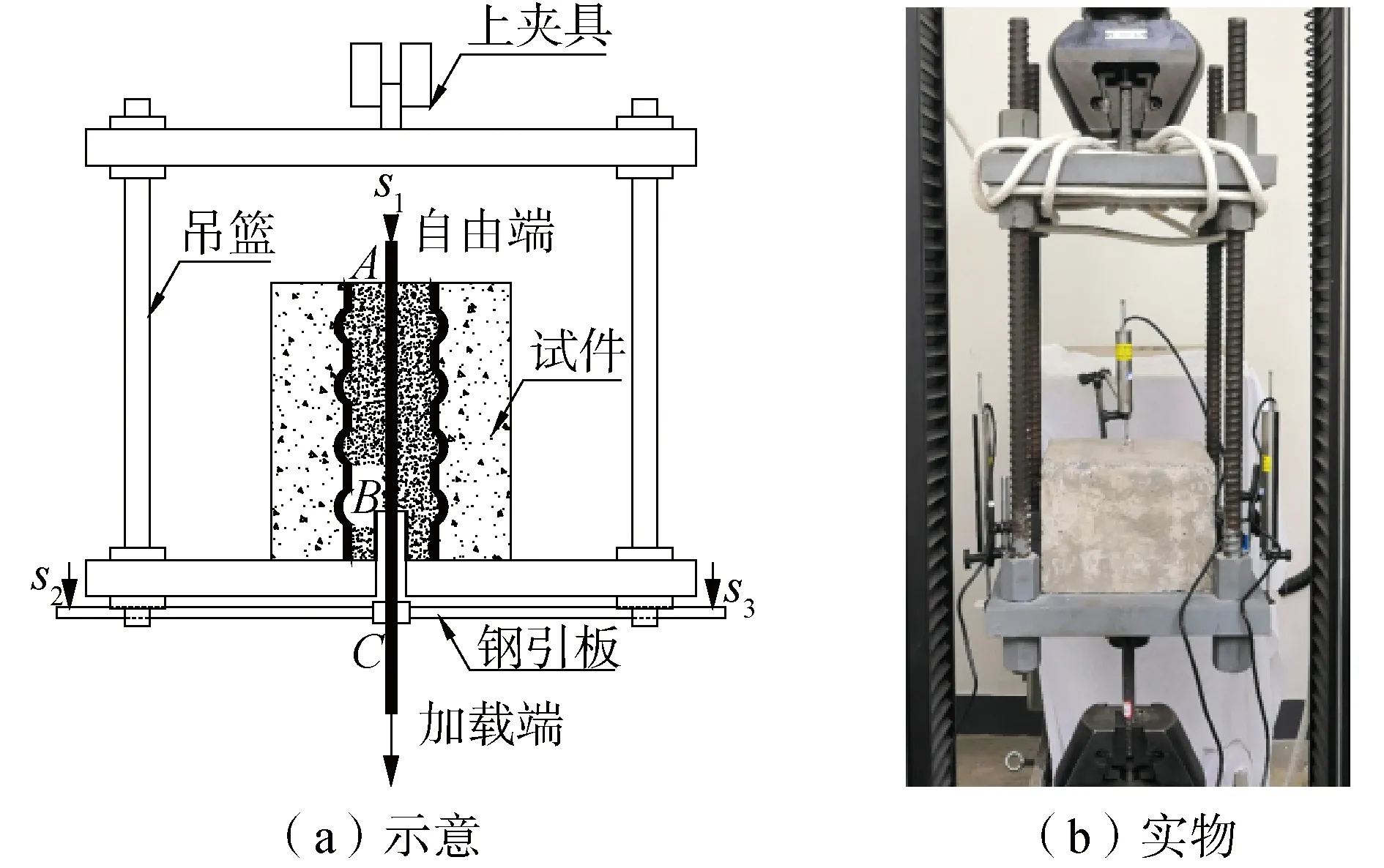
图3 加载装置及测点布置Fig.3 Test setup and measuring point location

2 试验现象及分析

2.1 试验现象

对15组基准试件进行了中心拉拔试验，各组试件的破坏形式均为钢筋滑移破坏，未出现波纹管滑移或混凝土开裂等现象。随着荷载的增加，钢筋应力逐渐由加载端向自由端传递。当自由端的灌浆料达到极限粘结强度时，试件滑移破坏加速，伴有机械咬合齿剪断的声音，并在钢筋和灌浆料之间形成光滑稳定的滑移破坏面，具体如图4所示。当锚固长度不大于5d时，钢筋与灌浆料间的粘结应力可取锚固长度范围内粘结应力的平均值[2]，即τa=F/πdla，试件的试验结果如表3所示。

图4 试件破坏形式Fig.4 Failure model of specimens

2.2 极限粘结强度影响因素分析

当孔径比一定，极限粘结强度随锚固长度的变化规律如图5所示。由图5可知，极限粘结强度随锚固长度的增加基本呈线性下降的趋势。这是由于随着锚固长度的增加，粘结应力的分布趋向不均匀[11]。在外荷载作用下，加载端粘结应力较大，当自由端达到极限粘结强度时，加载端已发生滑移破坏，降低了粘结应力平均值。

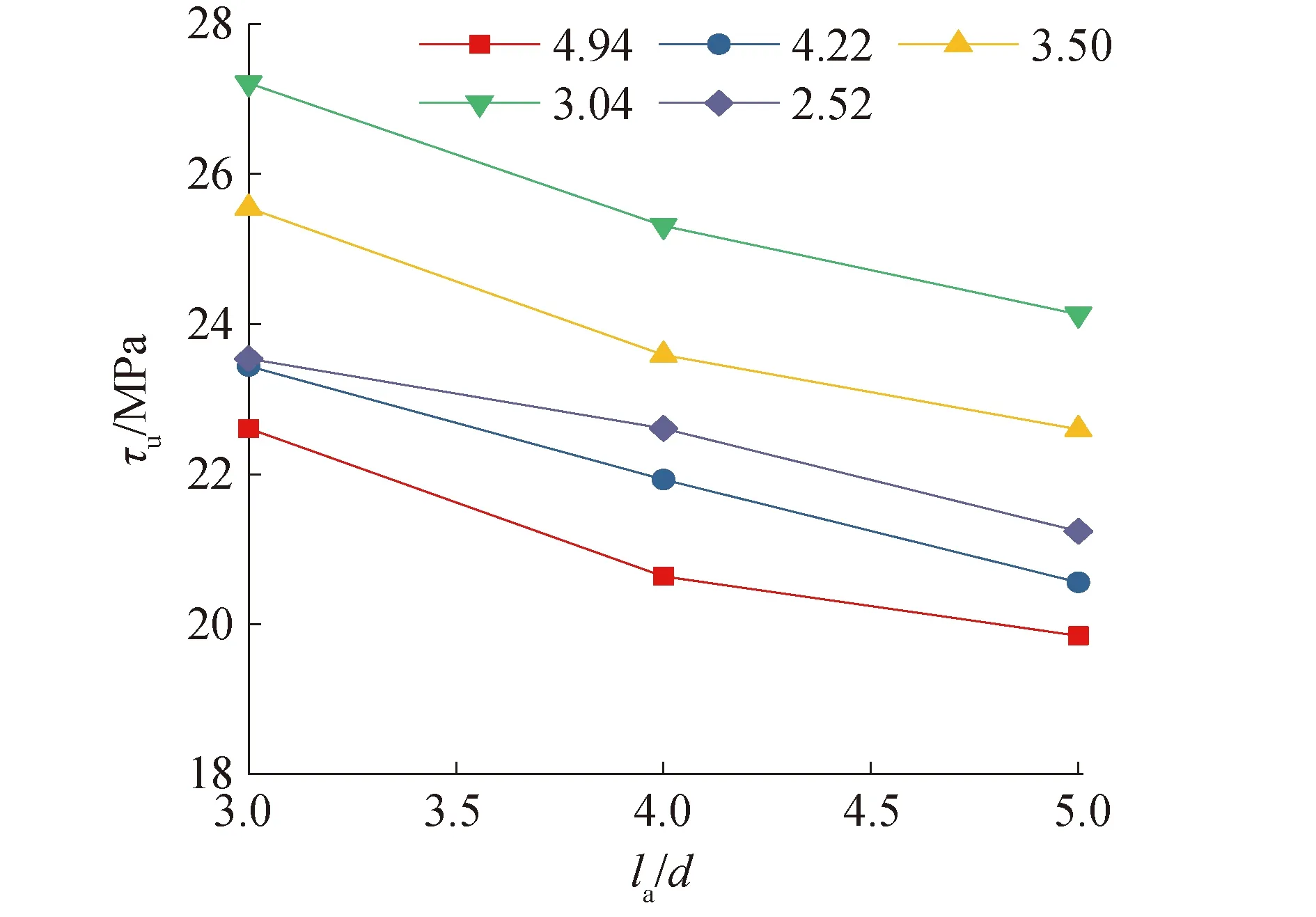
图5 极限粘结强度随锚固长度的变化Fig.5 The variation of ultimate bond strength with anchorage length

当锚固长度一定，极限粘结强度随孔径比的变化规律如图6所示。随着孔径比的增大，极限粘结应力呈先增后减的变化规律。在孔径比D/d=3.04处，极限粘结应力取得较大值，锚固性能表现最佳。在外荷载作用下，钢筋月牙肋会对灌浆料产生斜向压力，轴向分力使灌浆料受剪，径向分力使灌浆料受拉。且钢筋与灌浆料间的粘结力由化学胶结力、摩擦力和机械咬合力组成，化学胶结力在较小的力作用下就被克服[12]。因而当孔径比较大时，浆料层饱满，在外力作用下，钢筋的径向压力使灌浆料产生膨胀，金属波纹管的环向约束有效抑制灌浆料的变形和裂缝的发展，增强了钢筋与灌浆料间的摩擦和机械咬合作用，使极限粘结强度增大。当孔径比过大时，金属波纹管的环向约束减弱，灌浆料易受剪发生滑移破坏，使极限粘结强度降低。

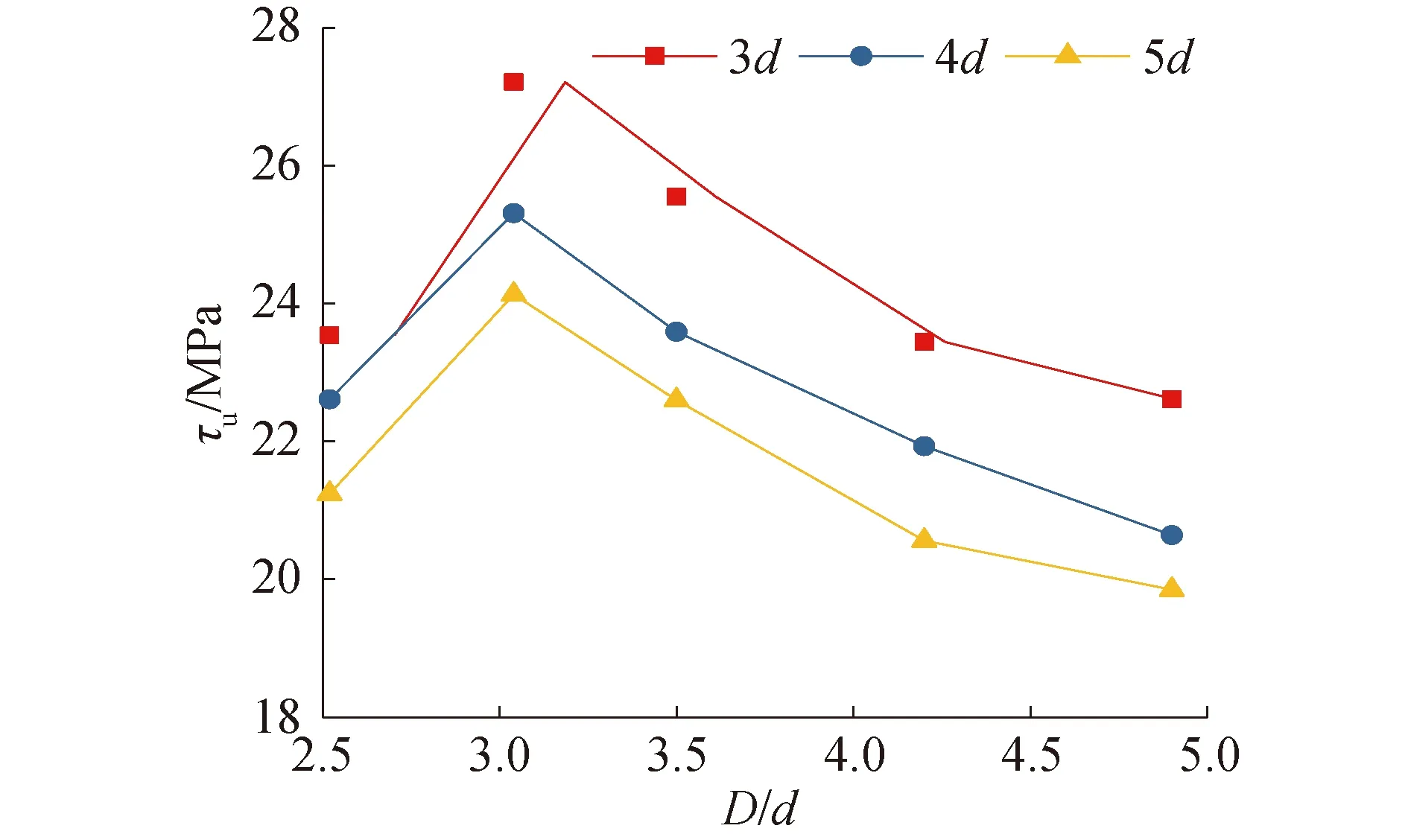
图6 极限粘结强度随孔径比的变化Fig.6 The variation of ultimate bond strength with diameter ratio

3 粘结-滑移本构关系模型

3.1 粘结滑移基本关系

各组基准试件的平均粘结应力-滑移量曲线如图7所示。粘结-滑移曲线大致可划分4个阶段：滑移段、劈裂段、下降段和残余段，具体如图8所示。加载初期处于滑移段，粘结力主要由钢筋月牙肋与灌浆料之间的机械咬合力提供，粘结应力与滑移量之间基本呈线性变化，滑移量较小。当加载至滑移后期，滑移量增长至1～2 mm，肋前灌浆料不断被挤压，开始出现剪切破坏现象。随着荷载的继续增加，粘结应力增长至极限粘结应力的80%左右，滑移量增长加快，粘结滑移曲线斜率开始连续降低，肋前灌浆料大面积发生压碎破坏，逐渐在钢筋周围形成环形破坏区，此阶段为劈裂段。当压碎破坏区延伸至自由端时，开始进入下降段。自由端粘结应力达到极限强度，钢筋与灌浆料之间的机械咬合齿不断被剪断，失效退出工作，粘结力不断下降，滑移量持续增长。在金属波纹管的环向约束和月牙肋轴向剪切的共同作用下，月牙肋和肋间灌浆料组成新的滑移破坏面。当粘结应力下降至极限粘结应力的60%左右时，粘结应力不再下降，在一定范围内上下波动，此刻处于残余段，粘结力主要由滑移破坏面与周围浆料层间的摩擦力提供。

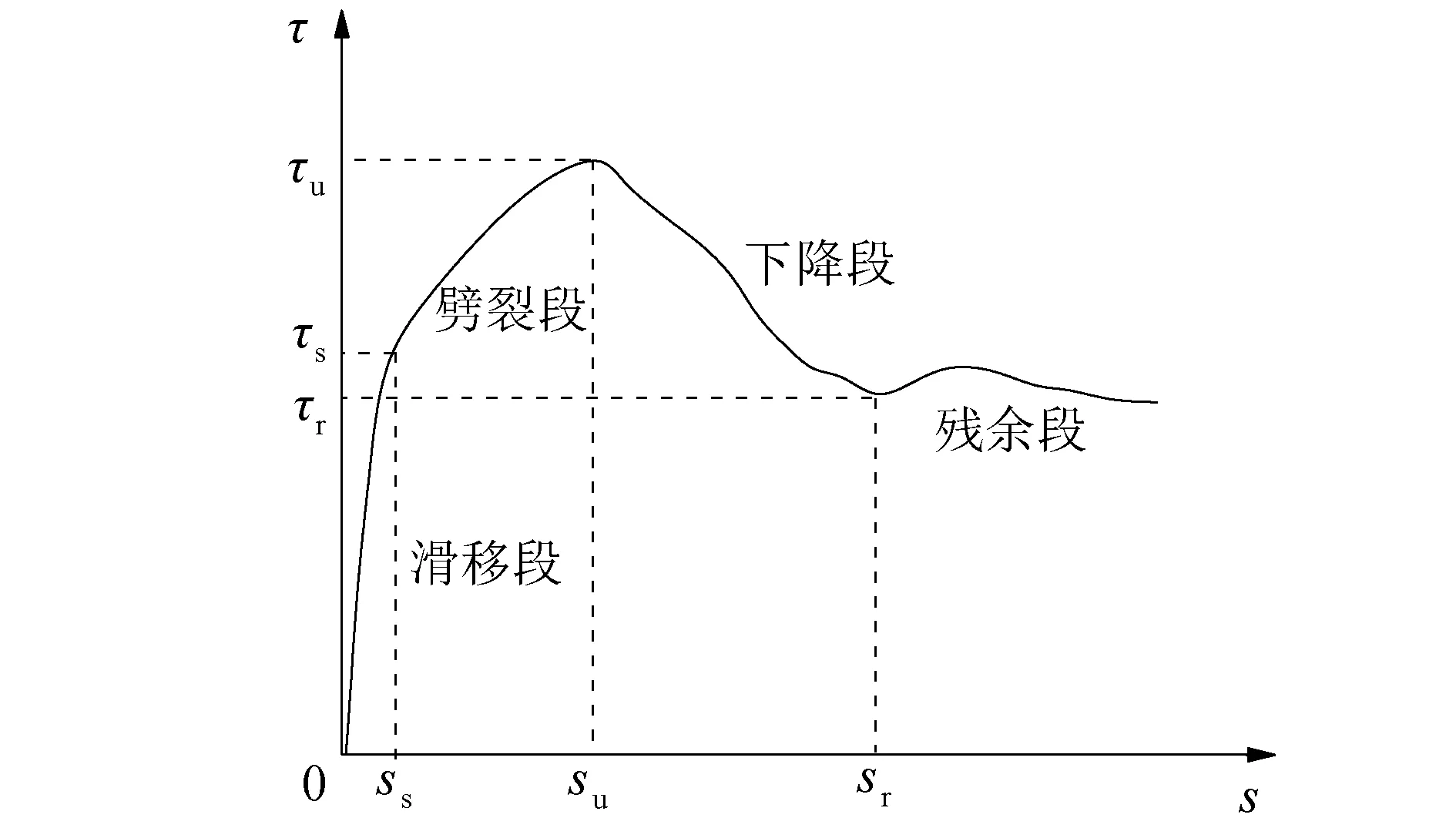
图8 粘结应力-滑移量关系模型Fig.8 Relationship model of bond stress-slip

由本文第2节可知，钢筋与波纹管约束灌浆料间的粘结性能与锚固长度、孔径比等因素有关。已有研究表明，粘结性能还受灌浆料强度影响[13-14]。考虑以上参数，并结合已有相关学者的本构关系模型[2,15]，对30个基准试件的粘结-滑移曲线进行拟合，可得粘结应力τ(s)与滑移量s之间的变化关系：

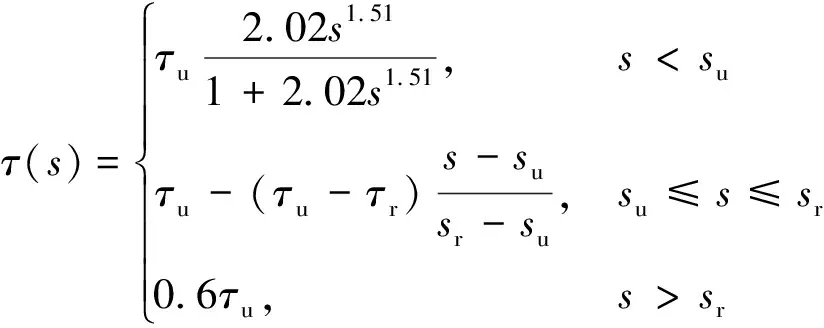
(1)

式(1)中的分段函数包含3部分，第1段为滑移段和劈裂段，采用幂函数描述，第2段为下降段，采用线性函数描述，第3段为水平残余段，采用常函数描述。由图7可知，粘结应力-滑移量关系的拟合曲线和试验曲线吻合较好。依据表3，对粘结应力-滑移量关系曲线上的特征点进行拟合：

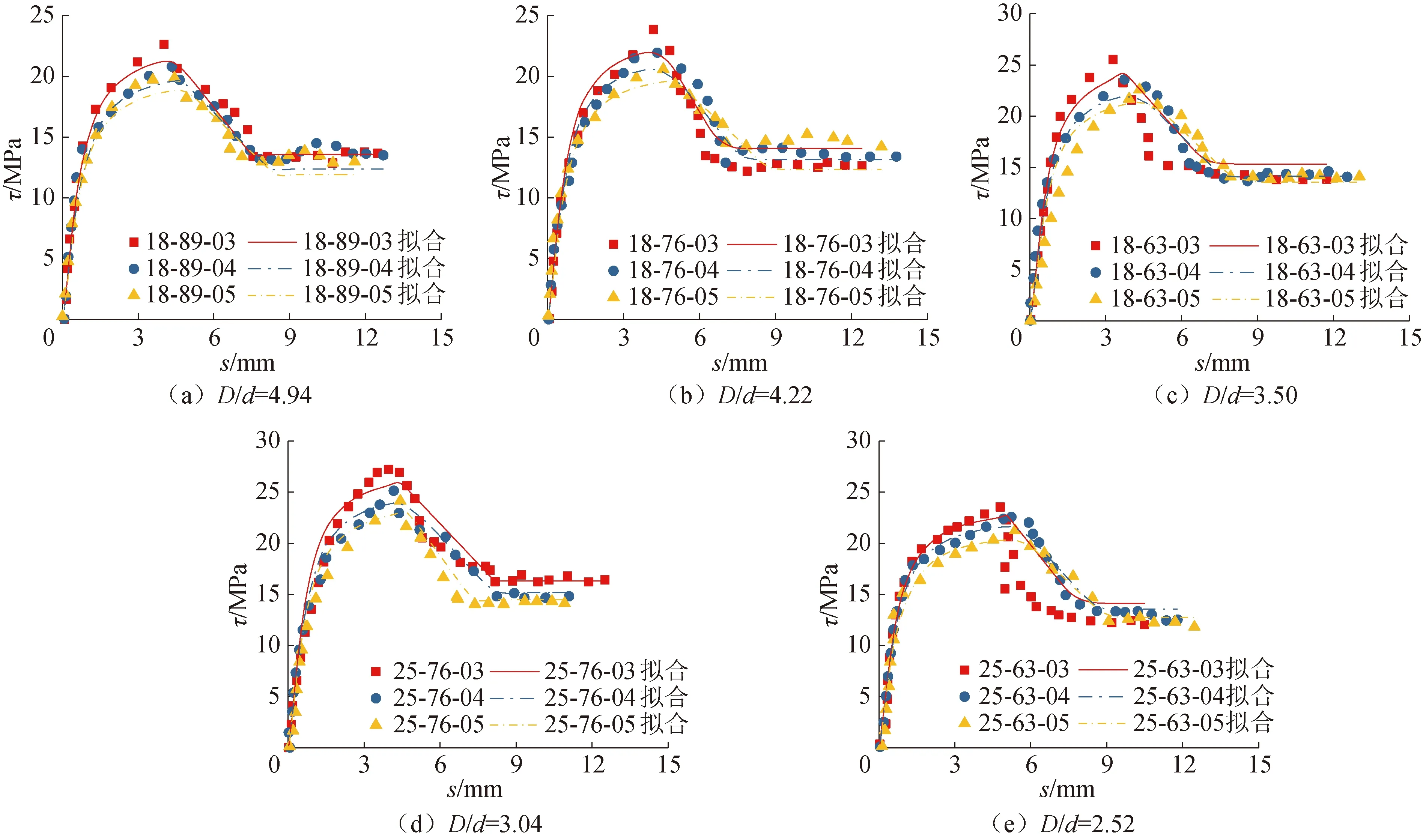
图7 粘结应力-滑移量关系曲线拟合值与试验值对比Fig.7 Comparisons of calculated bond stress-slip curve with test results

(2)

(3)

τr=0.6τu

(4)

(5)

其拟合值与试验值的对比如表4所示。由表4可知，拟合值能较好地反映试验数据。

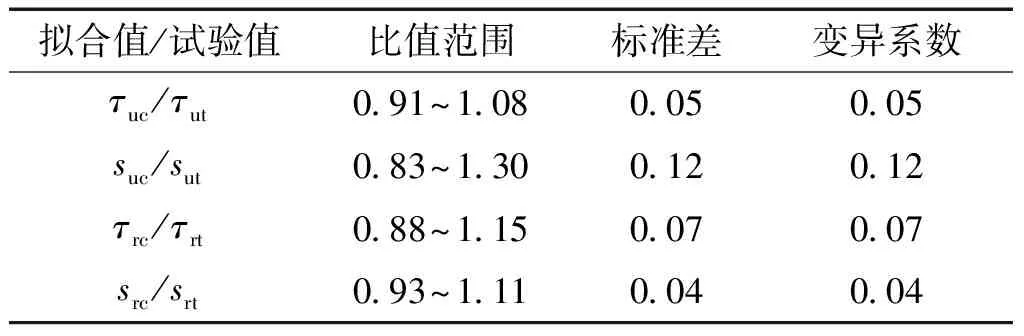
表4 粘结应力-滑移量曲线特征点拟合值与试验值对比

3.2 粘结应力分布位置函数

已有文献研究表明：随着锚固长度的增加，粘结应力不再均匀分布[16-17]。为探究钢筋与波纹管约束灌浆料间的粘结应力分布规律，本文对10个钢筋开槽试件进行了中心拉拔试验。通过测量不同荷载作用下，钢筋沿锚固长度范围内的应变分布和变化，可获取各点的粘结应力分布：

(6)

式中：σs、εs、Es为钢筋的应力、应变和弹性模量。

为便于各组试件间的横向对比，对粘结应力和粘结长度进行无量纲化处理，分别除以平均粘结应力τa和锚固长度la。各组试件从自由端至加载端的粘结应力分布如图9所示。由图9可知，粘结应力沿锚固长度方向呈单波峰状分布，在距离自由端0.75la附近，粘结应力取得峰值。不同荷载作用下，粘结应力分布曲线的形状表现出较好的一致性。加载初期，力主要由加载端附近的粘结力承担，粘结应力尚未发展至自由端，其分布的不均匀性最为显著。随着荷载的增加，力沿锚固长度向自由端传递，粘结应力分布曲线峰值降低，不均匀程度减弱，曲线形状趋向稳定。对比不同孔径比下的粘结应力分布曲线可知，各曲线变化规律总体一致。当孔径比D/d较大时，粘结应力分布曲线峰值有降低趋势，粘结应力分布更均匀，灌浆料可充分发挥工作性能。

通过对图9的粘结应力分布曲线进行拟合，即可得到粘结应力分布位置函数φ(x)(即为τ/τa)：

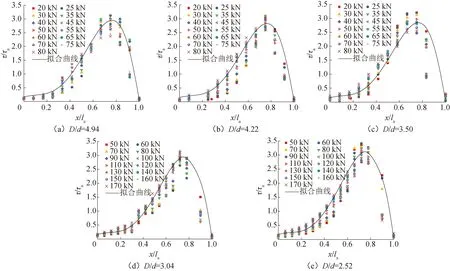
图9 粘结应力分布曲线拟合值与试验值对比Fig.9 Comparisons of calculated bond stress distribution curve with test results

(7)

由图9可知，粘结应力分布拟合曲线与试验曲线能较好地吻合。将平均粘结应力-滑移量基本关系式τ(s)和反映粘结应力分布变化的位置函数φ(x)组合，即为钢筋与波纹管约束灌浆料之间完整的粘结应力-滑移量本构关系模型：

τ(x)=τ(s)φ(x)

(8)

4 结论

1)各组基准试件的破坏形式均为钢筋滑移破坏；当锚固长度la为3d～5d，孔径比D/d为2.52～4.94时，极限粘结强度随锚固长度la的增加基本呈线性降低趋势，随孔径比D/d的增大呈先增后减的变化规律，且当孔径比D/d=3.04时，极限粘结应力取得较大值，锚固性能表现最佳。

2)各组钢筋开槽试件在不同荷载作用下，粘结应力沿锚固长度la方向呈单波峰状分布，在距离自由端0.75la附近，粘结应力取得峰值；当孔径比D/d较大时，粘结应力分布更为均匀，灌浆料可充分发挥其工作性能。

3)通过对试验数据拟合，建立了考虑锚固长度la、孔径比D/d等因素并能反映粘结应力分布变化的粘结-滑移本构关系简化模型，该模型与试验结果能较好地吻合，可为进一步开展灌浆金属波纹管钢筋连接有限元分析等提供有益参考。