钢筋插入式波纹管浆锚连接受力性能数值分析
2021-06-10石棚王浩柳家为朱克宏
石棚, 王浩, 柳家为, 朱克宏
(1.东南大学 混凝土及预应力混凝土教育部重点实验室,江苏 南京 210096;2.中铁二十四局集团有限公司, 上海 200070)
预制拼装桥梁由于克服了传统施工中构件质量无法保证、生产效率低下、交通拥堵以及粉尘污染等问题[1-3],其在桥梁建设改造工程中得到越来越广泛的应用。其中,预制构件主要受力钢筋之间的可靠连接是保证节段预制拼装桥梁整体性的关键[4-6]。
灌浆套筒连接技术自20世纪60年代被提出以来,至今已发展成为预制构件连接的主要技术之一[7-8]。为了探明套筒灌浆连接的锚固性能及受力机理,国内外学者对其进行了试验及理论研究。Ling等[9]研究了连接钢筋锚固长度以及套筒直径对灌浆套筒接头连接性能的影响。Raynor等[10]进行了灌浆套筒接头的循环荷载试验,分析了其在周期荷载作用下的粘结性能。郑永峰等[11-12]提出了一种新型变形灌浆套筒,通过试验研究以及有限元分析,研究了其连接性能及工作机理。然而,有学者提出,传统灌浆套筒内部构造复杂,加工制作难度大,在现场施工过程中无法保证安装及灌浆质量。陈俊等[13]采用波纹管代替灌浆套筒,并对这种新型连接技术进行了试验研究,结果表明该方法施工简便、连接可靠。王志强[14]等对灌浆套筒与灌浆波纹管进行了抗震性能研究,结果表明两种连接方式的各向性能与现浇试件无明显差异。贾俊峰等[15]对基于波纹管浆锚连接的预制拼装RC墩柱进行了试验研究,结果表明其侧向刚度与现浇墩柱基本一致,可用于强震区构件拼装。
为了进一步研究钢筋插入式波纹管浆锚连接技术的锚固性能及受力机理,本文基于有限元法对其进行了单轴拉伸模拟研究,并与现有文献试验结果对比,分析钢筋锚固长度la、灌浆料厚度rg和钢筋直径ds对其连接性能的影响。
1 数值模型
该模型包含钢筋、灌浆料、波纹管和混凝土4种材料,为保证接头轴向拉伸数值模拟的准确性,有限元模型的材料本构关系应与实际材料属性相吻合。此外,模型包含3类接触面,对接触界面进行处理时,应根据各界面的接触特性选择合适的分析方式。
1.1 材料本构模型
1.1.1 钢筋和波纹管
钢筋材料属性采用陈俊等[7]材性试验数据。其屈服强度为451.2 MPa,抗拉强度为591.7 MPa,设定弹性模量为206 GPa,本文中钢筋采用三折线各向同性硬化材料模型,如图1 (a)所示。波纹管采用双线性随动强化材料模型,设定其屈服强度为400 MPa,弹性模量为206 GPa,如图1 (b)所示。
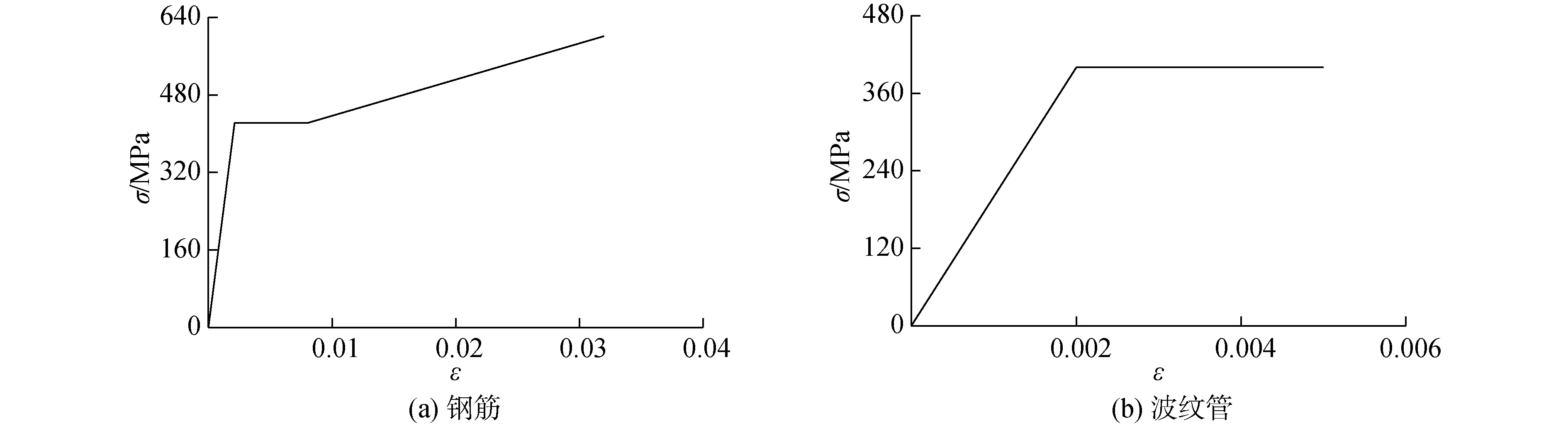
图1 材料本构关系Fig.1 Mechanical properties of materials
1.1.2 灌浆料和混凝土
灌浆料和混凝土都采用多线性各向同性硬化材料模型,其受压应力-应变关系[16]:
(1)
(2)
式中:σ为材料的压应力;ε为材料的压应变;fc为材料的抗压强度;Eg为材料的弹性模量。
灌浆料和混凝土材料属性采用陈俊等[13]材性试验所得数据,灌浆料抗压强度为53.4 MPa,设定弹性模量为30 GPa,其抗拉强度[7]:
ft=0.62(fc)1/2
(3)
式中:ft为材料的抗拉强度。
图2 (a)所示为灌浆料的应力应变关系。混凝土抗拉强度为43.1 MPa,设定弹性模量为30 GPa,如图2 (b)所示。2种材料的破坏准则皆采用William-Warnke 5参数准则。
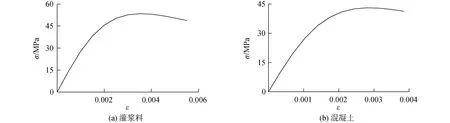
图2 材料本构模型Fig.2 Mechanical properties of materials
1.2 有限元模型
模型包含钢筋-灌浆料、灌浆料-波纹管以及波纹管-混凝土3类接触界面。钢筋和混凝土的粘结本构关系极其复杂,国内外学者对其进行了大量试验研究,并采用粘结单元进行数值模拟,其效果良好,因此本文对钢筋-灌浆料界面采用分离式粘结模型。然而,波纹管波肋增强了其接触界面的机械咬合作用,故本文采用库伦摩擦模型对灌浆料-波纹管接触界面和波纹管-混凝土接触界面进行模拟,摩擦系数μ取0.4[18]。采用ANSYS建立1/4接头模型,1/4纵截面施加对称约束,混凝土侧面固定,如图3所示。钢筋和波纹管采用实体单元SOLID185模拟,SOLID65模拟灌浆料和混凝土,接触单元TARGE170和 CONTA174模拟波纹管两界面的粘结,非线性弹簧单元COMBIN39模拟锚固钢筋与灌浆料之间的粘结应力-滑移关系,其粘结滑移本构关系为[19]:

图3 有限元模型Fig.3 Finite element model
(4)
式中:τ钢筋和灌浆料粘结应力;s钢筋和灌浆料之间的相对滑移;k1线性段斜率,k1=τcr/scr劈裂段斜率;k2=(τu-scr)/(su-scr);k3下降段斜率,k3=(τr-τu)/(sr-su)。
2 模型验证
为验证数值模型的准确性,采用陈俊等[7]试验与有限元模型进行对比,试验装置如图4所示。利用有限元方法模拟25-12-07d和25-12-10d波纹管接头的轴向拉伸试验,模拟结果见表1,其中Py和P′y分别为接头试验和模拟的屈服荷载,Pu和P′u分别为接头试验和模拟的极限荷载。由表1可知,接头25-12-07d和接头25-12-10d轴向拉伸试验和数值模拟得到的屈服荷载误差分别为0.68%和1.04%,极限荷载误差分别为2.56%和6.63%,模拟结果与试验误差较小。图5所示为接头有限元分析所得荷载-位移曲线和试验数据对比结果。由图5可知,数值模拟荷载-位移曲线的变化趋势同试验结果基本吻合,误差较小,证明了有限元模型的可靠性。
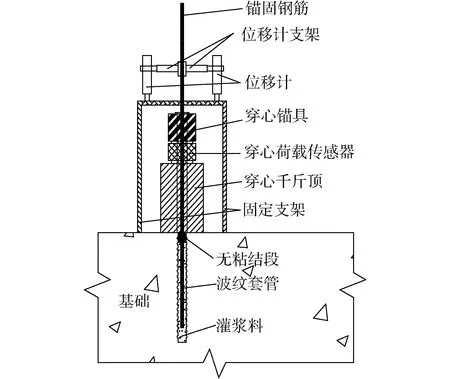
图4 试验加载装置Fig.4 Test setup arrangement

表1 波纹管接头轴向拉伸试验与模拟结果对比Table 1 Comparison between experimental and simulated results
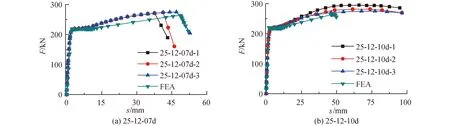
图5 有限元分析与试验结果荷载-位移曲线Fig.5 Load-displacement curves of experimental and FEA
3 参数分析
3.1 有限元模型参数
根据陈俊等[7]试验研究,影响接头锚固性能的因素包括锚固长度、灌浆料厚度及钢筋直径等。数值模型中锚固长度分别取7d,10d,10d和20d,其中d为锚固钢筋直径;钢筋直径分别取18、25、32和40 mm;灌浆料厚度分别取6、12、20和28 mm,波纹管直径根据钢筋直径与灌浆料厚度确定。数值模型几何构造如图6所示,尺寸参数如表2所示,rg为灌浆料厚度,l为锚固长度,ln为无粘结段长度。
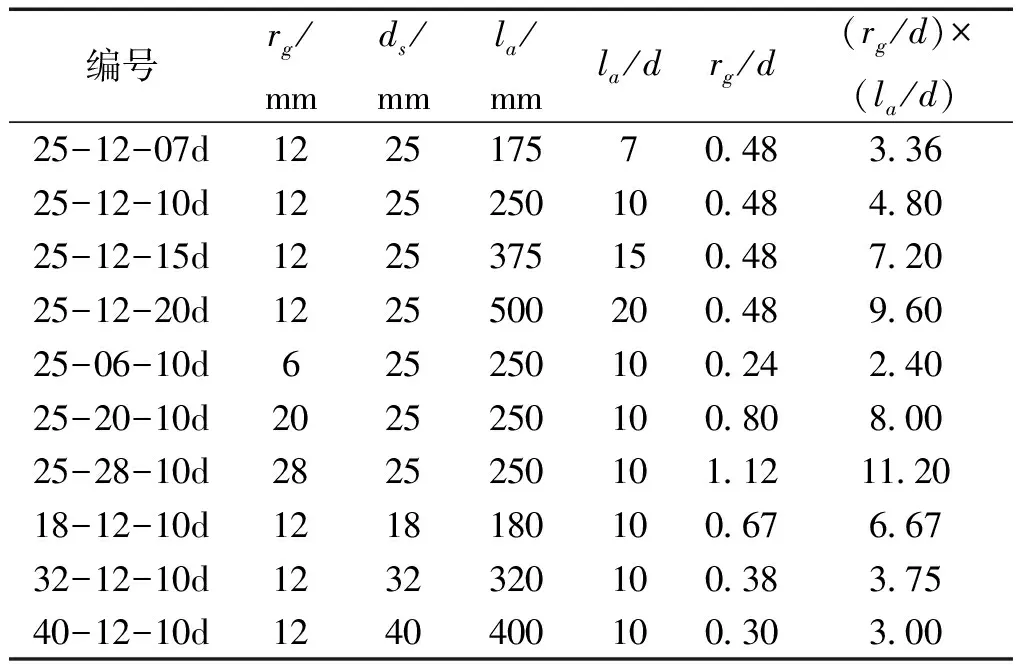
表2 数值模型尺寸参数Table 2 Details of the numerical model
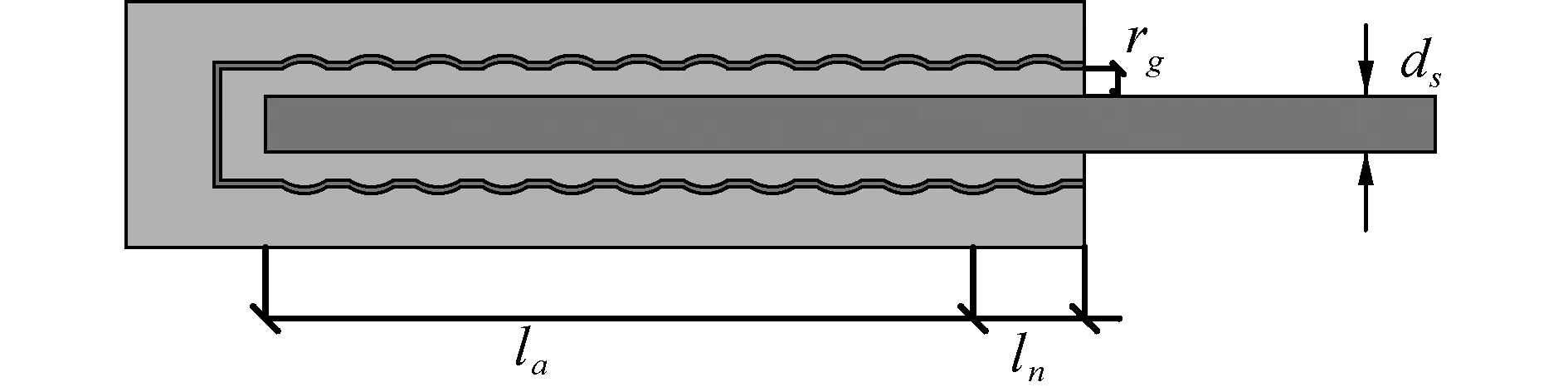
图6 数值模型几何构造Fig.6 Geometric construction of numerical model
3.2 极限抗拉强度与承载力
表3和图7所示分别为波纹管接头极限抗拉强度和承载力对比曲线。其中fu为波纹管接头的极限抗拉强度(fu=Pu/ds),fbyk为连接钢筋的屈服强度标准值,fbuk为连接钢筋的极限抗拉强度标准值。
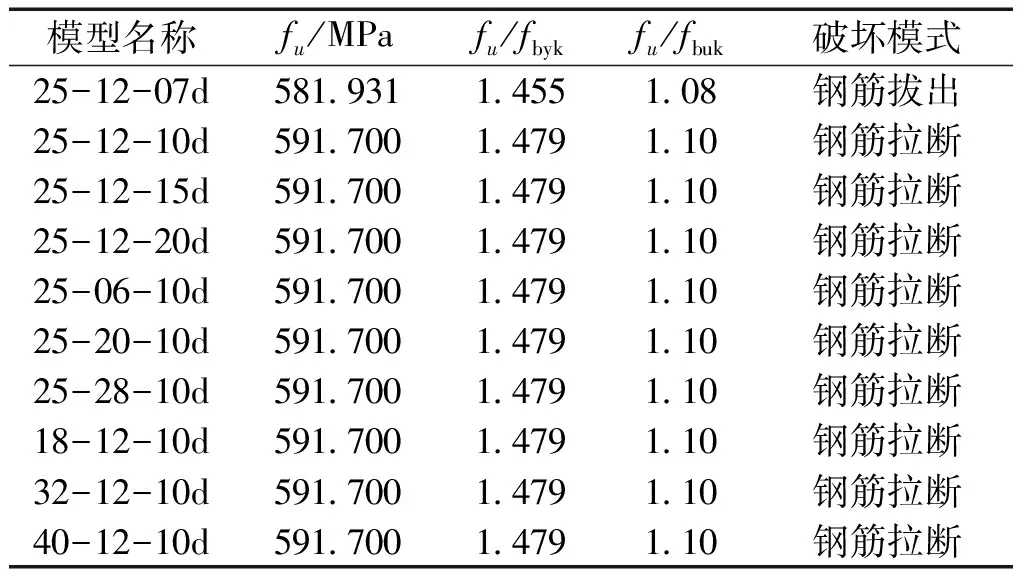
表3 有限元模拟结果Table 3 Results of the FEA
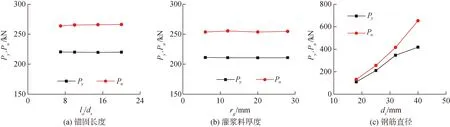
图7 承载力对比曲线Fig.7 Comparison of bearing capacity curves
由表3和图7可知,除锚固长度为7d的接头破坏模式为钢筋拔出破坏外,其余接头的破坏模式均为钢筋拉断破坏,为理想破坏模式,且接头极限抗拉强度与钢筋屈服强度标准值的比值fu/fbyk>1.25,接头极限抗拉强度与钢筋抗拉强度标准值的比值fu/fbuk>1.1,满足JGJ 107-2010《钢筋机械连接技术规程》中I级接头中单向拉伸强度要求。
3.3 荷载-位移曲线
3.3.1 锚固长度对荷载-位移曲线的影响
不同锚固长度接头的荷载-位移曲线如图8 (a)所示。由图可知,接头25-12-07d在达到钢筋极限抗拉强度之前发生粘结破坏,在外荷载作用下,承载力迅速下降。其余3种接头的荷载-位移曲线变化趋势一致,达到钢筋的极限抗拉强度之后,仍保持一定的承载能力,是接头理想的失效模式。
3.3.2 灌浆料厚度对荷载-位移曲线的影响
不同灌浆料厚度接头的荷载-位移曲线如图8 (b)所示。由图可知,尽管接头灌浆料厚度存在差异,但其在单向荷载作用下的F-s曲线变化趋势及极限承载力相似,表明接头极限承载力和灌浆料厚度无明显相关性,在单向受力状态下,接头的破坏形式均为钢筋屈服破坏,满足接头设计要求。
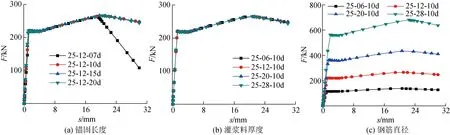
图8 数值模拟F-s曲线结果Fig.8 F-s curves of the FEA
3.3.3 钢筋直径对荷载位移曲线的影响
不同钢筋直径接头的荷载-位移曲线如图8(c)所示。由图可知,接头的屈服荷载及极限荷载与钢筋直径相关,不同钢筋直径接头的破坏模式均为钢筋拉断破坏,为理想失效模式。
3.3.4 灌浆料应力
各接头灌浆料与混凝土的应力分布如图9所示。由图可知,灌浆料和混凝土的应力分布随波肋呈锯齿状分布。接头25-12-07d,25-06-10d和40-12-10d波肋处灌浆料及混凝土最大应力均已超过两材料抗压强度(分别为53.4和43.1 MPa),表明灌浆料及混凝土在轴向拉伸作用下将发生压碎破坏。其余接头灌浆料和混凝土应力分布较均匀,最大应力分布在顶部非粘结段的第1个波肋处,均未超过2材料抗压强度,整体粘结效果良好,符合要求。
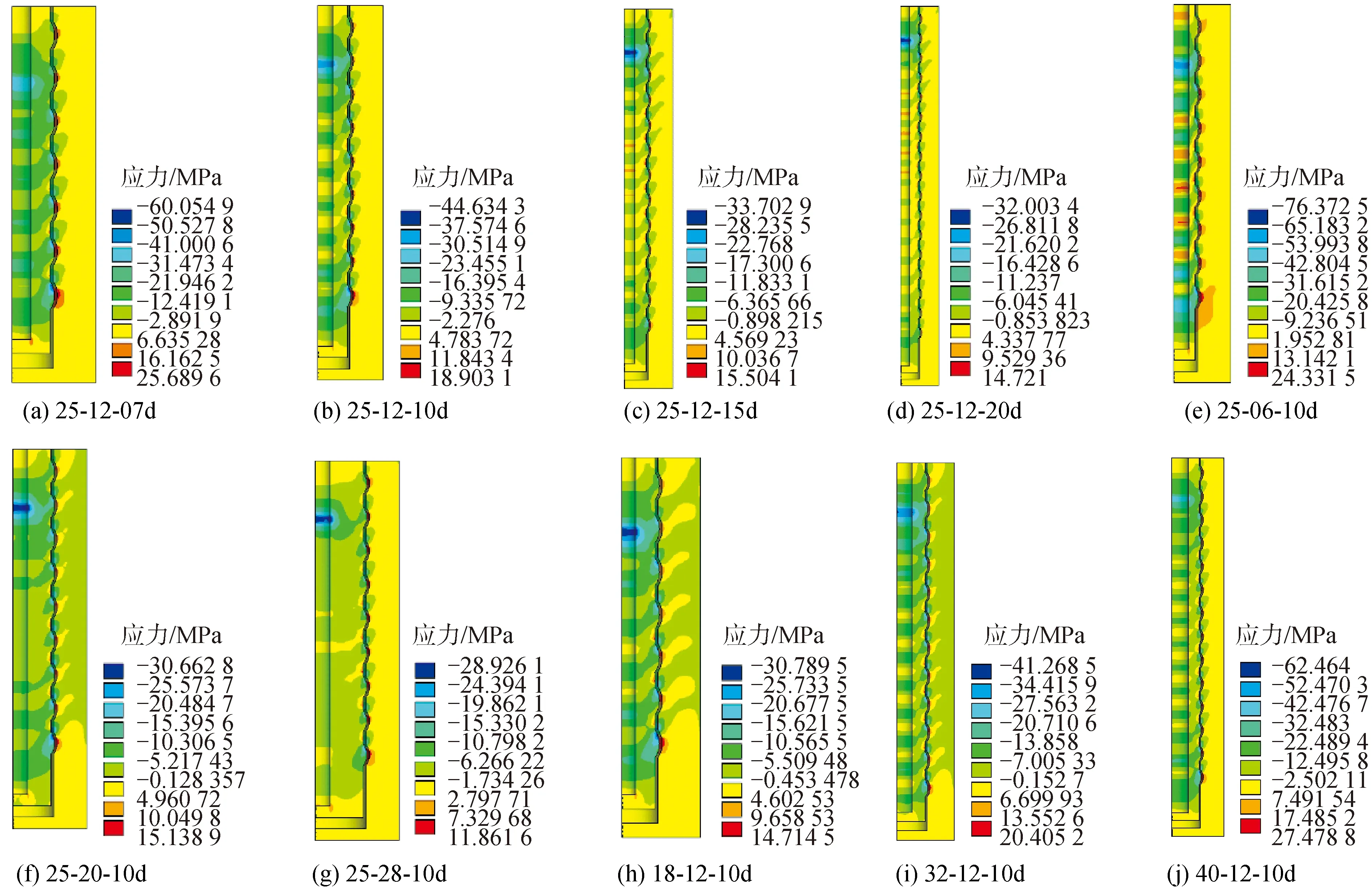
图9 灌浆料及混凝土轴向应力分布Fig.9 Distribution of axial stress of grouting material and concrete
3.3.5 波纹管应力
各接头波纹管应力分布如图10所示。由图可知,不同接头其波纹管的应力分布存在差异。25-12-15d和25-12-20d接头波纹管最大应力出现在顶部第3、4个波肋处,而其余接头波纹管的最大应力出现在底部第1个波肋处,表明锚固长度为波纹管应力分布主要影响因素。此外,所有波纹管最大应力均未超过140 MPa,低于其屈服强度,在外荷载作用下,波纹管一直处于弹性阶段,无破坏危险。
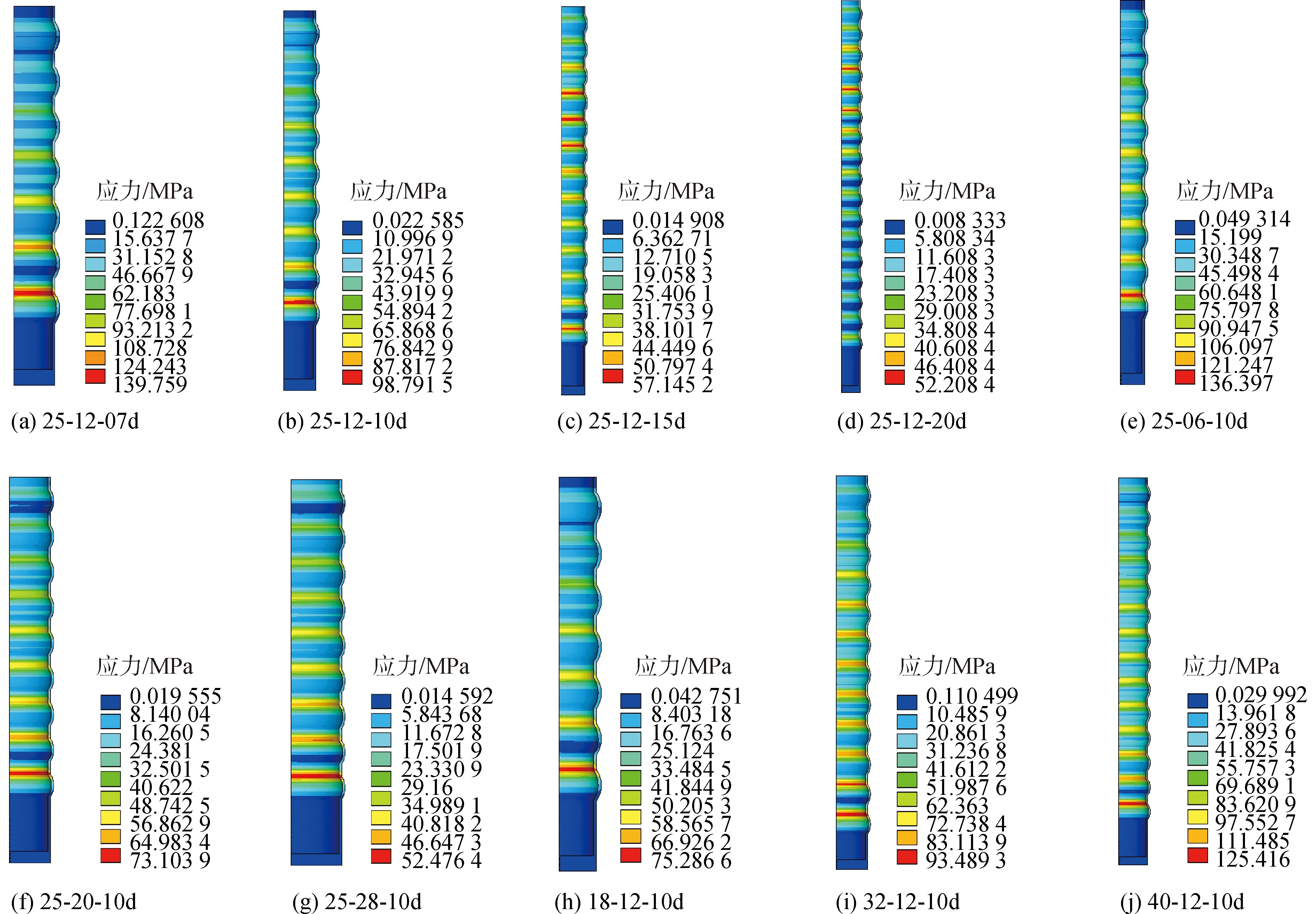
图10 波纹管Mises有效应力分布Fig.10 Distribution of von Mises stress of corrugated sleeve
3.4 参数综合分析
不同rg/ds及rgla/ds所对应的灌浆料与混凝土最大轴向压应力如表4所示,不同rg/ds及rgla/ds对灌浆料与混凝土应力分布的影响如图11所示。由表4和图11可知,随着rg/ds和rgla/ds增大,σg,max及σc,max减小;当rg/ds<0.3或rgla/ds<3.0时,σg,max>53.4 MPa,σc,max>43.1 MPa,灌浆料及混凝土压碎;当rg/ds>0.8,rgla/ds>9.6时,随其值增大,σg,max及σc,max继续减小,但降幅不明显。
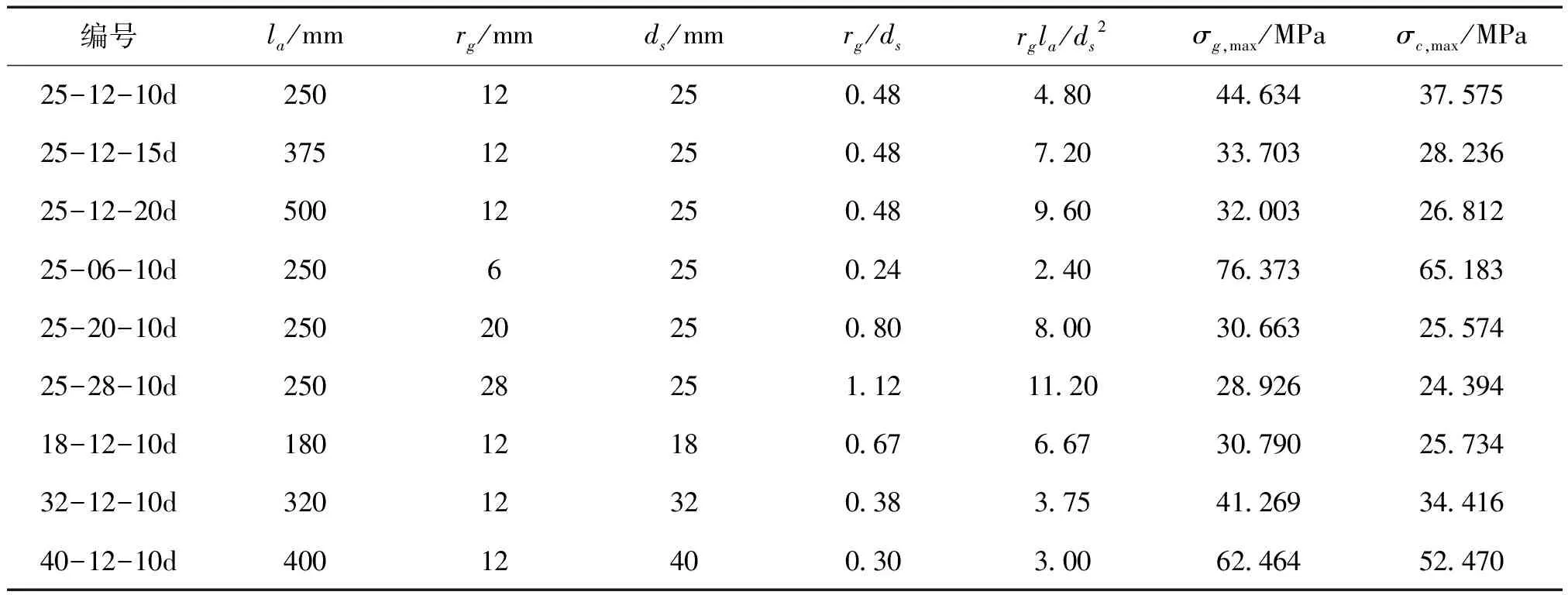
表4 rg/ds及rgla/ds对灌浆料及混凝土应力分布的影响Table 4 Effect of rg/ds and rgla/ds on stress distribution of grouting material and concrete
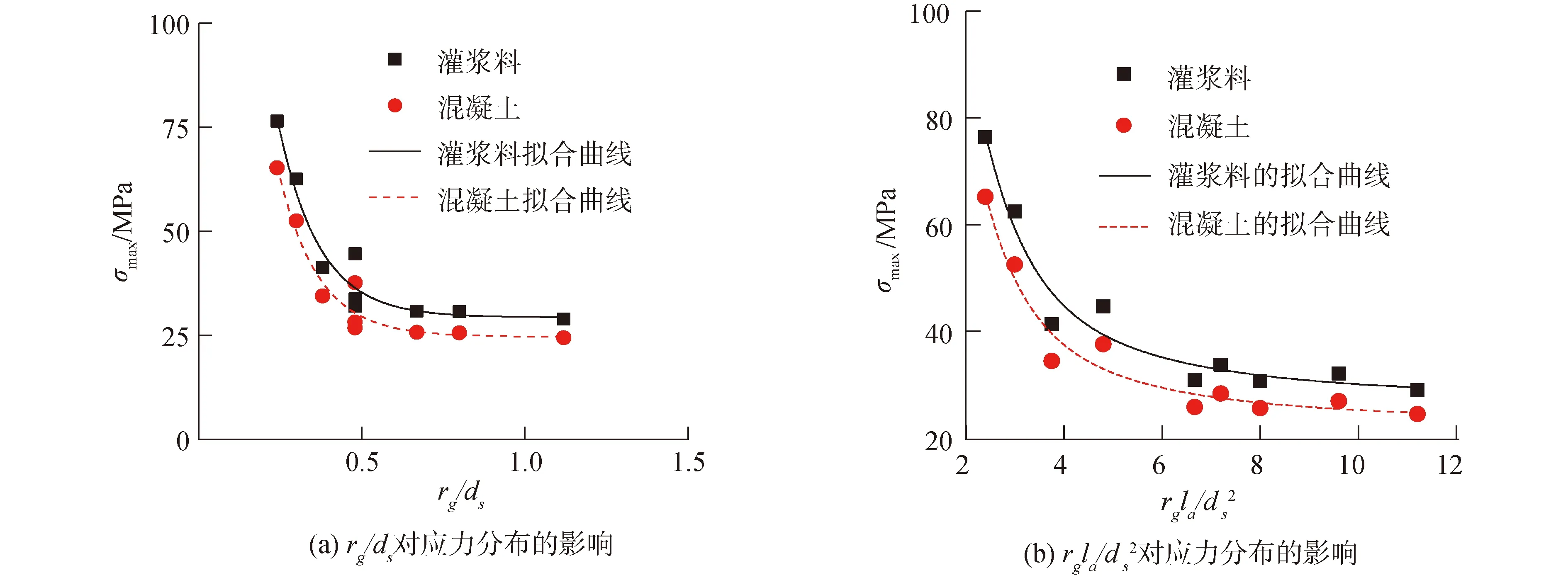
图11 rg/ds及rgla/ds对灌浆料及混凝土应力分布的影响曲线Fig.11 The influence curves of rg/ds and rgla/ds on stress distribution of grouting material and concrete
4 结论
1)对比试验与有限元分析得到的荷载-位移曲线及极限荷载,表明选用模型可以较有效地模拟波纹管接头的受力性能。
2)钢筋锚固长度la、灌浆料厚度rg和钢筋直径ds影响接头的破坏模式,当la≤7ds时,接头主要破坏模式为粘结破坏,当la≥10ds时,接头以钢筋屈服破坏为主,当rg/ds<0.3或rgla/ds<3.0时,接头灌浆料及混凝土发生压碎破坏。
3)波纹管在轴向拉伸过程中,其最大应力均未超过材料屈服强度,一直处于弹性阶段。
4)建议灌浆料厚度与钢筋直径之比rg/ds取值在0.3~0.8,灌浆料厚度与锚固长度的乘积与钢筋直径平方之比rgla/ds取值在3.0~9.6。
