单层SnS薄膜的光吸收特性及应变调控：基于第一性原理计算的GW-BSE方法

李文涛

(陕西科技大学 文理学院， 陕西 西安 710021)

0 引言

自从石墨烯被发现以来，由于其新奇的电子结构和物理性质，使得人们对这类层状二维材料的研究产生了浓厚的兴趣[1].近年来，越来越多的二维材料相继被发现和制备出来，包括过渡金属硫化物、氮化硼、黑磷、硅烯和硼烯等[2].其中，由Ⅳ族和Ⅵ族元素(如Sn、Ge和S、Se等)组成的一类层状化合物，每层拥有和黑磷类似的结构，层间则由较弱的范德瓦尔斯力相互连接，因此在这类结构中也能够实现单层的二维薄膜[3].单层SnS作为这类新型二维材料的代表，由于其能带中存在带隙，并且组成元素在自然界含量丰富，成本低廉且无毒无害，因而在表面催化、吸附、光电和热电等领域具有广阔的应用前景[4].近来，已有研究报道在实验中成功制备出单层SnS的二维薄片[5]，也有研究工作指出其载流子的迁移率可能较MoS2高[6].

二维材料的电子结构和带隙宽度直接决定了其在电子器件、光催化以及太阳能电池和光电及传感等领域中的可能应用前景[7].因此，探索以SnS为代表的这类新型二维半导体材料的电子结构，揭示其的能带类型和带隙宽度等，进而阐明其光吸收特性，以及针对这些物性可能实现的调控手段等，是进一步拓展其在低维人工器件和光电应用领域的迫切需求.针对单层的SnS薄膜，近年来已有部分理论研究工作揭示了其中缺陷的形成以及过渡金属元素掺杂对材料电子结构的影响[8].此外，还有理论研究工作给出单层SnS表面对有害气体分子的吸附及载流子调控，发现其在气体传感方面也有较大的应用潜力[4].

但是，目前理论研究工作都是采用以密度泛函理论(DFT)为基础的第一性原理计算方法，虽然其能够给出这类二维材料的电子结构，但是利用DFT方法得到的带隙宽度理论结果往往较实验值偏低，进而影响到对这类低维材料光吸收特性的判断和理论预测[9].通过引入杂化泛函等方法能够进一步提高DFT关于电子结构和带隙宽度的计算准确度，但是其计算量往往较大；同时材料的光吸收过程中将在价带和导带中产生空穴和电子对，两者通过库仑作用形成激子，因此通过单粒子近似的DFT方法也不能够准确描述材料的光吸收特性[9].因此，本文以第一性原理计算为基础的多体格林函数理论为基础，采用GW近似方法，揭示了准粒子近似下单层SnS薄膜的电子结构，给出了关于其能带类型和带隙宽度更加准确的理论计算结果.利用单层SnS薄膜经过准粒子修正后的电子结构，结合描述电子和空穴对的Bethe-Salpeter方程(BSE)，进一步揭示了这类二维材料中的介电常数和光吸收特性.

应变是调控材料物性的重要手段，特别是对于薄膜和二维材料等低维结构[10].因此研究不同应变对这类新型二维材料电子结构等物性的影响，就可能为在这类二维材料上实现低维电子器件和光电应用等提供可能途径.因此，本文在单层SnS薄膜电子结构的理论计算基础上，进一步研究了二维材料面内施加的不同应变对能带类型和带隙宽度以及光吸收系数的影响和可能调控.本文的研究结果不仅揭示了单层SnS薄膜的电子结构和光吸收特性，表明了这类新型二维材料在光电等领域中的应用前景，而且也为今后进一步开展以这类二维材料为基础的低维电子器件的制备和应用等提供了理论研究基础和依据.

1 计算方法

本文中关于二维材料SnS的第一性原理计算是通过开源的QUANTUM ESPRESSO (QE) 程序平台实现[11].第一性计算基于DFT理论，采用广义梯度近似下的PBE(Perdew-Burke-Ernzerhof)交换关联泛函，为了比较计算得到的材料带隙宽度，计算中还使用了杂化泛函HSE(Heyd Scuseria Ernzerhof)泛函.计算利用平面波和超软赝势的方法，在布里渊区内的积分是通过16×16×1的Monkhorst-Pack网格实现，计算中平面波的截断能为50 Ry，迭代计算中力和能量的收敛判据分别为1×10-3Ry/Bohr和10-7Ry.文中关于应变的计算是在平衡晶格结构的基础上，分别沿着面内晶胞的单轴或者双轴施加从+15%到-15%的区间(以2%间隔取系列离散值)内不同拉伸和压缩数值来实现不同应变下晶胞计算.

基于多体微扰理论的GW近似方法是通过Yambo程序包实现[12]，计算是在第一性原理计算的基础上，将多体格林函数理论中准粒子的自能算符通过GW近似实现，进而通过迭代求解Dyson方程实现，最终可将准粒子自能当作交换关联泛函的微扰带入到Kohn-Sham方程中，实现电子结构激发态的准粒子修正.材料光吸收特性的计算是基于准粒子自能计算中介电函数的计算，计算中采用了无规相近似(random phase approximation,RPA)，通过求解Bethe-Salpeter方程实现[9,12,13].

2 结果与讨论

2.1 单层SnS薄膜的晶格结构

单层SnS薄膜的原子结构如图1所示.每个Sn原子和近邻的三个S原子成键，排列成和黑磷类似的铰链结构.图中还分别用红色虚线框和蓝色实线框给出了单层SnS晶胞和布里渊区示意图.结构模型中X轴沿着薄膜面内的Zigzag方向，Y轴指向薄膜的Armchair方向[14].

图1 单层SnS薄膜晶格结构示意图

通过第一性原理计算能够得到单层SnS薄膜的基态晶格结构.计算给出二维面内x和y方向的晶格常数分别为4.045埃和4.340埃(数值计算的收敛精度在0.001埃)，与文献报道结果比较接近[15].为了进一步验证二维结构的稳定性，图2还给出了单层SnS的声子结构.由于晶格振动在Γ点处不存在虚频，表明了基态结构的稳定性.

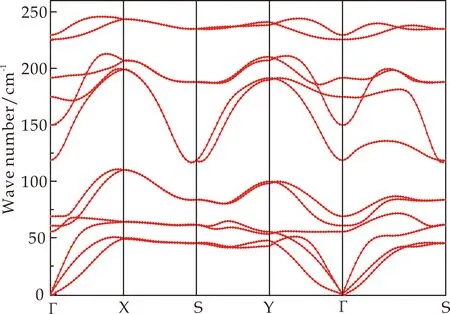
图2 单层SnS薄膜声子色散结构

2.2 单层SnS薄膜的电子结构

在单层SnS薄膜晶格结构计算的基础上，分别采用了PBE泛函、HSE杂化泛函以及GW近似方法给出了单层SnS薄膜的能带结构，费米面附近的计算结果如图3所示.图3中用不同颜色来区分不同的计算方法，并用虚线分别指出了PBE和GW方法下导带最低位置和价带最高位置的对应关系.可以看出所有方法都表明了单层SnS薄膜具有间接带隙的能带特征.虽然不同方法针对费米面附近各条能带都能给出比较接近的色散形貌，但是对于带隙宽度却有显著的差异.使用传统的PBE泛函，计算结果拥有最小的带隙宽度，数值为1.455 eV，这和过去文献报道中普遍认为DFT计算会低估材料带隙宽度的结论相一致.使用杂化泛函以及准粒子的GW近似方法，能够给出更加准确的带隙计算结果，分别为2.053 eV和2.493 eV.

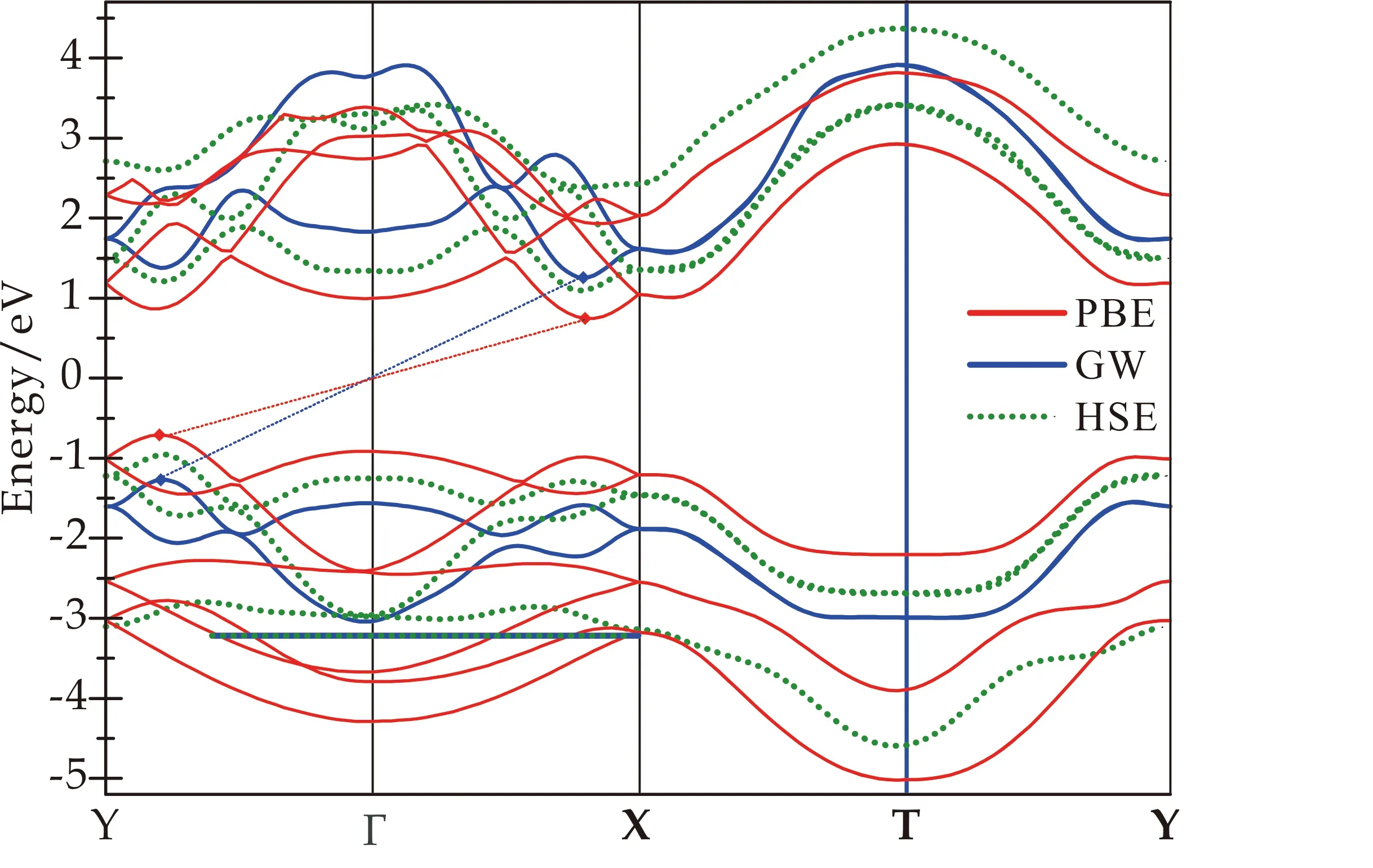
图3 单层SnS薄膜的能带结构

为了说明单层SnS薄膜中各原子轨道对能带结构的贡献，图4给出了电子态密度(DOS)和部分态密度(PDOS)的计算结果，其中费米能级取为0 eV.从图4可以看出，单层SnS中S原子和Sn原子形成化合键后，价带部分主要由S原子p轨道构成，导带部分则主要由Sn原子的p轨道构成.

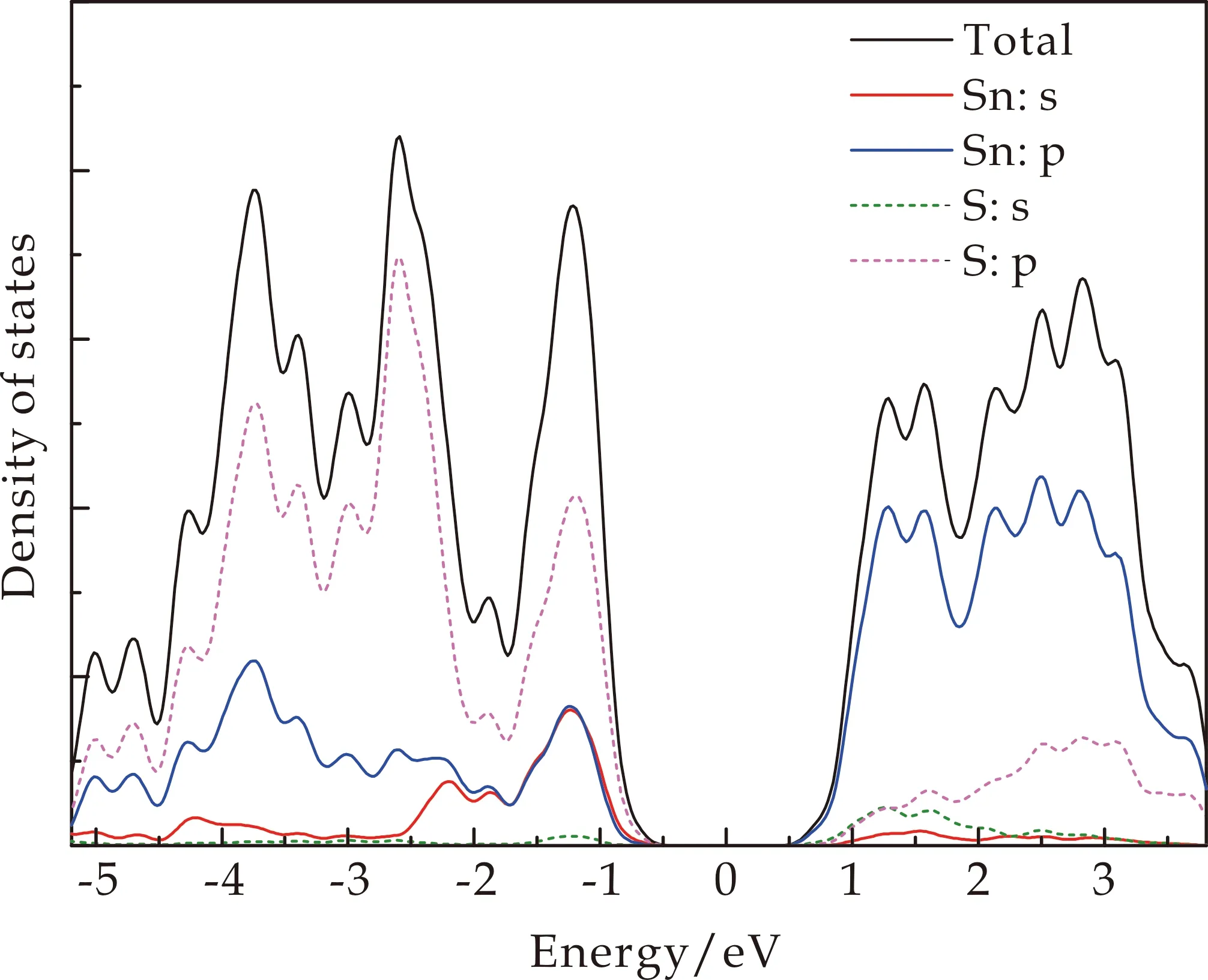
图4 单层SnS薄膜的电子态密度

2.3 单层SnS薄膜电子结构的应变调控

应变是调控低维材料物性的主要手段[16].针对单层SnS薄膜，通过在面内分别施加单轴和双轴应变，相应能带结构的变化在图5给出，其中所有结果均为准粒子GW方法下计算获得.图5(a)～(c)中用不同的颜色给出了费米能级附近3条导带和3条价带随着应变的变化特征：实线为无应变的结果，虚线和点划线分别对应于施加拉伸和压缩应变的结果，其中偏离实线越远，则代表施加的应变数值越大.计算中应变的数值从压缩应变的-15%到+15%之间取一系列离散值.图5(a)和(b)分别对应于沿着单轴x和y分别施加应变，而沿着xy同时施加应变的结果则在图5(c)中展示.

(a)沿着单轴x施加应变

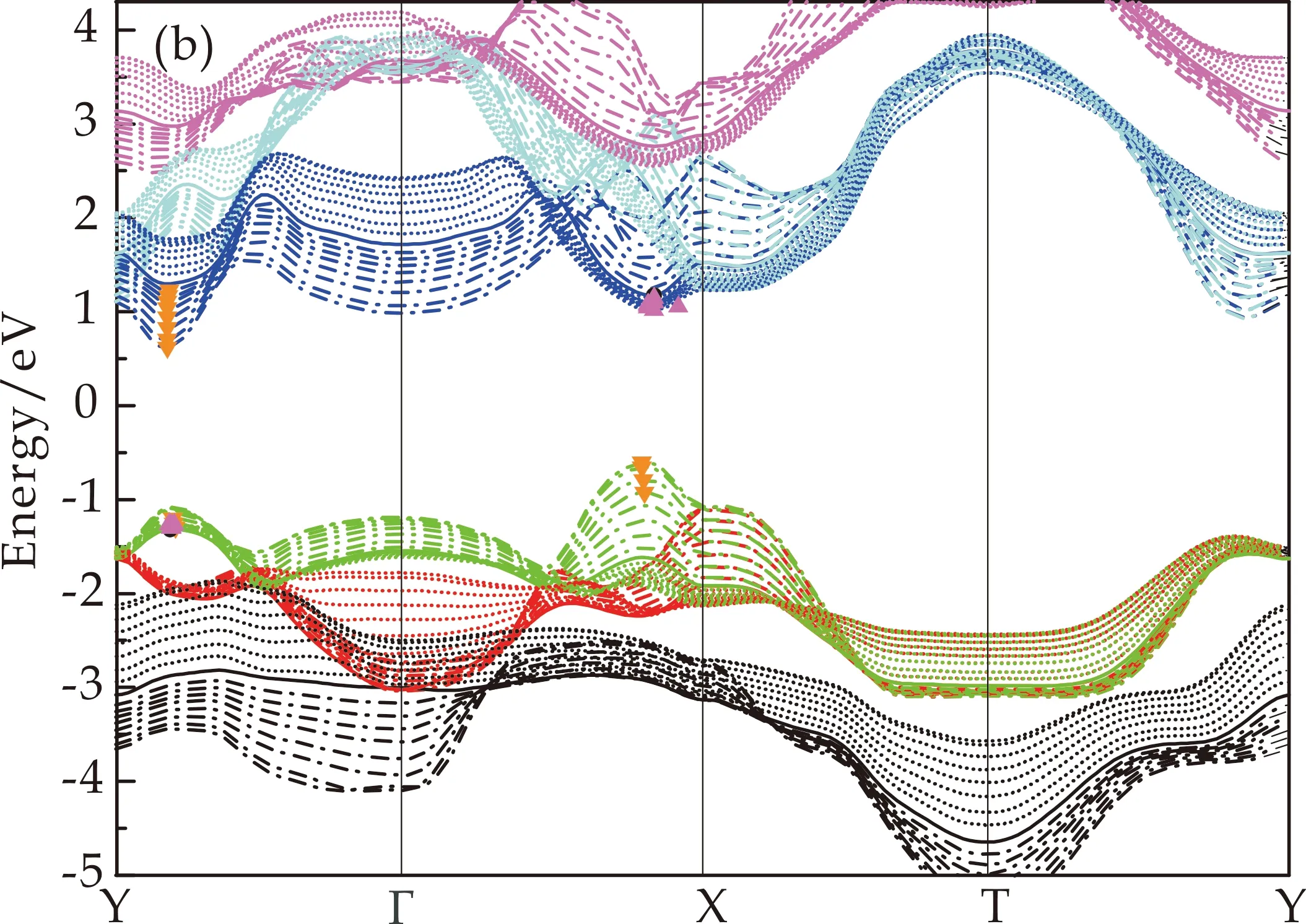
(b)沿着单轴y施加应变

(c)沿着双轴x和y同时施加应变

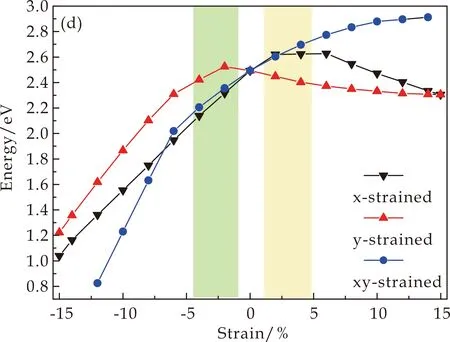
(d)不同应变下带隙宽度的变化图5 单层SnS薄膜不同应变下的GW能带结构

图5(a)～(c)中还分别用黄色和粉红符号标示出不同压缩和拉伸应变下导带底和价带顶所在的位置.计算结果表明，通过对单层SnS二维薄膜施加应变，能够有效调控其能带结构，包括带隙类型和带隙宽度都会随着应变发生变化.不同应变下带隙宽度的计算结果在图5(d)中给出，可以看出压缩应变下体系的带隙宽度都变小；拉伸应变下，双轴应变的带隙宽度会不断增大；单轴应变的带隙宽度变化较缓慢，表现为y向应变会使带隙宽度小幅度下降，而x方向则小幅升高后下降.除了带隙宽度的变化，计算结果还发现通过在x和y方向分别施加应变，可以实现单层SnS薄膜从间接带隙向直接带隙的转变，转变发生在如图5(d)中绿色和黄色覆盖的应变区域，分别对应于x方向2%～5%的应变区间以及y方向-2%～-5%的区间.

2.4 光吸收特性及应变调控

在电子结构计算的基础上，进一步研究了GW-BSE方法下单层SnS薄膜的光吸收特性.图6给出了无应变下单层SnS薄膜介电函数的计算结果，并且包含了电子和空穴相互作用即激子的影响.介电函数实部和虚部的计算结果分别在图6(a)和(b)中展示，图中还分别用红色和蓝色给出了考虑和不考虑激子的计算结果对比.可以看到电子和空穴的相互作用对单层SnS的介电函数的计算具有显著的影响，这也说明为了更加准确的反应材料的光吸收特性，必须在计算中考虑电子和空穴的相互作用.

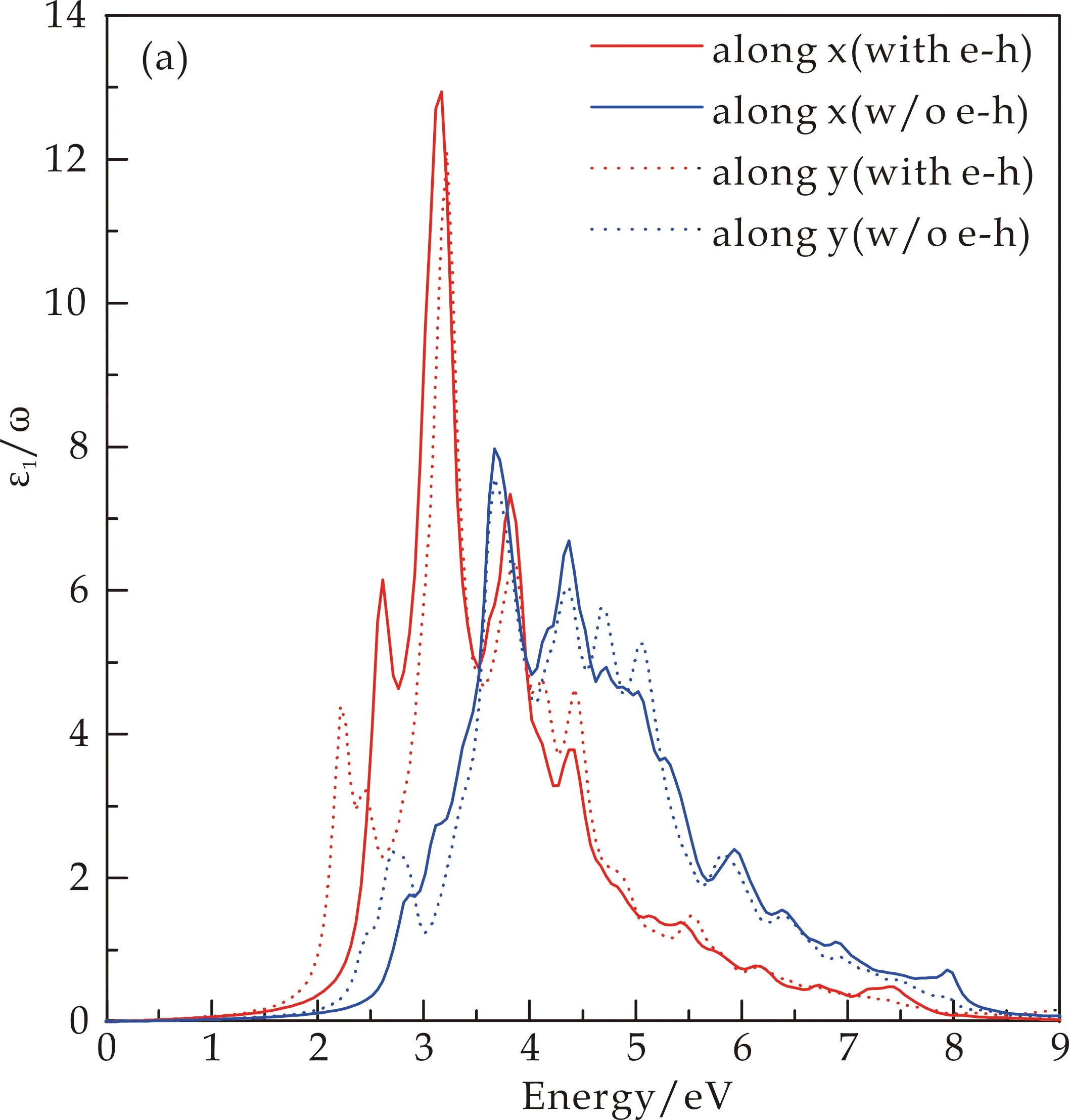
(a)介电函数的实部

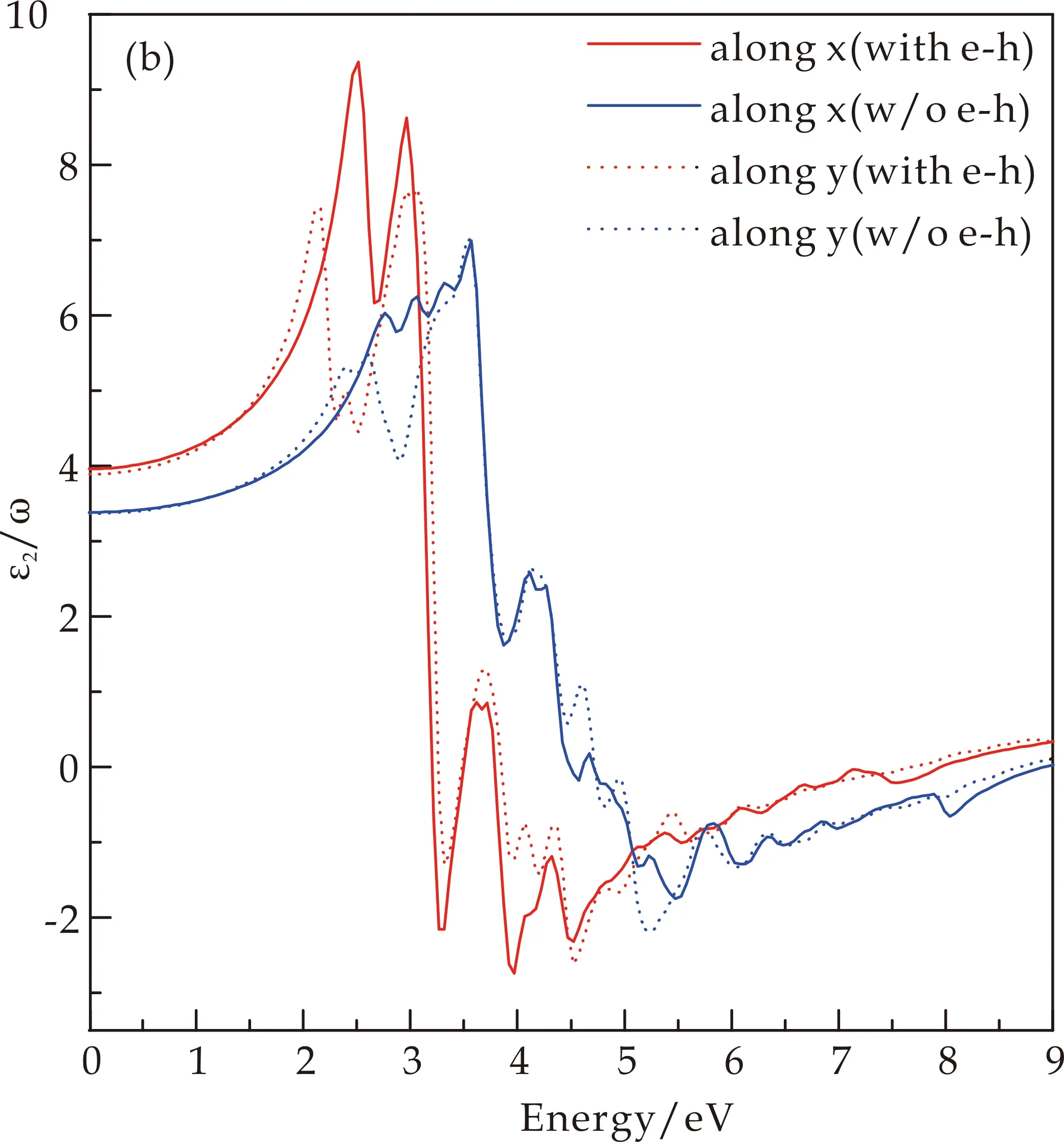
(b)介电函数的虚部图6 单层SnS薄膜的介电函数

由于单层SnS薄膜在面内具有各向异性的晶格结构，如图1原子结构所示.因此，在图6介电函数的计算中还考虑了入射电场强度矢量沿着x和y方向的影响，分别用实线和虚线表示.计算结果也进一步验证了单层SnS薄膜介电性质的各向异性.通过介电函数的计算就能够给出材料的光吸收特性，计算结果如图7和图8所示.

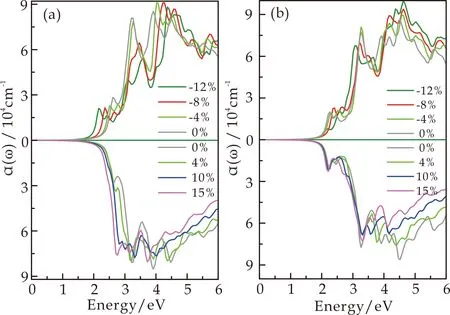
(a)电场强度矢量沿着 (b)电场强度矢量沿着面内X轴 面内Y轴图7 X轴不同应变下单层SnS的光吸收系数

图7和图8分别为单层SnS薄膜在沿着X轴和Y轴不同应变下材料光吸收系数的计算结果，图中上下部分分别对应于压缩和拉伸应变的计算结果，其中所有计算都是考虑了电子和空穴的相互作用.图7和图8中(a)和(b)分别为电场强度矢量沿着面内X轴和Y轴的计算结果.通过对比以上计算结果，可以发现无论是沿着X轴还是Y轴施加应变，材料光吸收系数吸收峰的起点位置在压缩应变下均逐渐降低.这和图5中不同应变下能带色散关系的计算结果是相一致的.由于压缩应变下带隙宽度的降低，导致光吸收的起点数值降低.同时，在X轴方向施加拉伸应变时，材料的光吸收特性表现出较强的各向异性特征，即图7(a)和(b)中下半部分曲线的区别，而其余应变下均不明显.这也说明通过对单层SnS薄膜在X轴方向施加拉伸应变，能够显著增强材料光吸收的各向异性.

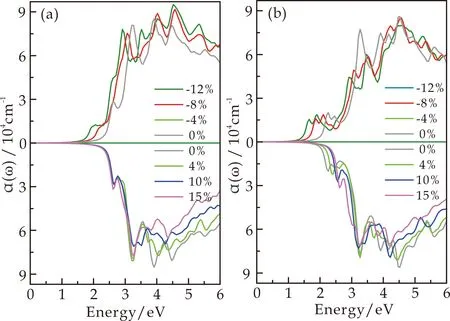
(a)电场强度矢量沿着 (b)电场强度矢量沿着面内X轴 面内Y轴图8 Y轴不同应变下单层SnS的光吸收系数

3 结论

本文基于第一性原理计算的GW近似方法和BSE方程，研究了单层SnS薄膜的电子结构和光吸收特性.通过GW计算方法给出了单层SnS薄膜更加准确的能带特征和带隙宽度的数值.在以上理论计算的基础上，本文还详细揭示了针对二维材料SnS施加不同应变对材料能带特征的影响和调控.计算结果表明通过对单层SnS施加不同应变，能够有效调控其带隙宽度的数值，并且当在面内X轴即Zigzag方向施加拉伸应变，Y轴即Armchair方向施加压缩应变时，单层SnS会发生间接带隙半导体向直接带隙半导体的转变.这可能为将来进一步在SnS上实现光电应用和器件制备提供理论基础.最后，通过对单层SnS薄膜介电函数和光吸收系数的计算，揭示了电子和空穴相互作用对半导体材料光吸收的影响，同时也发现通过在X轴施加应变，能够显著增强单层SnS薄膜光吸收的各向异性.本文的计算结果，可以为将来进一步在单层SnS薄膜上开展低维人工器件的制备以及拓展其在光电和传感等领域的应用提供理论依据.