基于激光雷达提取特征的改进匹配算法

任工昌, 刘 朋, 何 舟

(陕西科技大学 机电工程学院， 陕西 西安 710021)

0 引言

定位是自主移动机器人研究中首先要解决的问题，也是机器人即时定位与构图(Simultaneous Localization and Mapping,SLAM)技术中研究的关键问题.在SLAM算法中，为了避免机器人里程计的累积误差，需要将激光雷达扫描的数据与之前建立并实时更新的地图数据进行匹配，匹配算法的精度直接影响到机器人定位的精度.所以，匹配算法的研究成为自主机器人研究中的热点问题[1].

目前，在2D激光 SLAM 中，主流的扫描匹配算法包括[2]：迭代最临近点(Iterative Closest Point,ICP)[3]及PL-ICP(Point-to-Line ICP)[4]、栅格相关性扫描匹配(Correlation Scan Match,CSM)[5,6]、基于优化的方法[7,8]和基于特征的匹配[9,10]等算法.ICP算法是通过待匹配两帧点云欧式距离的最小化来求解变换矩阵R和T，该方法计算量偏大，且易受初值影响而陷入局部最优.CSM算法通过遍历匹配的方式排除了结果对初值的敏感性，经过分枝定界等方法降低了计算量，但总体计算速度较慢，且计算精度受限于栅格的精度.优化的方法通过给定一个目标函数，把激光雷达数据扫描匹配问题转换成非线性最小二乘优化问题，该方法可以限制误差的累积，但仍然对初值敏感.基于特征的匹配算法通过提取特征点，大幅降低了计算量，但是精度较高的特征点提取比较困难，角点特征的数量较少，而数量较多的线段特征，由于帧间相互遮挡导致同一特征在不同帧中提取的线段特征长度存在差异，无法直接进行匹配.

综上所述，目前的匹配算法较多，但存在初值敏感或计算量大等问题.因此，本文结合特征提取和ICP算法的特点，提出了一种基于提取特征的改进匹配算法，该算法通过计算扫描点的斜率差对点集进行分割，进而提取角点和线段，并计算其相应的特征值，然后再按照ICP的原理进行匹配.本算法在进行线段特征点匹配时，使用提取的线段中点坐标及线段斜率来计算两线段间的距离，代替原有算法中计算两点间距离，避免了因提取的线段长度不同而造成的匹配误差，进而提高了匹配的精度.

1 特征点提取

如图1所示，从O点向直线l以等角度Δθ的间隔画直线，假设交点依次为P1，P2，P3，P4,…,O点到交点的长度依次为ρ1，ρ2，ρ3，ρ4,…，然后，由P1点向OP2做垂线相交于P1′点，则φ1为直线l与P1P1′的夹角，同理可得φ2、φ3.

由几何关系可得：

φ3=φ2+Δθ=φ1+2×Δθ

因为：

当Δθ很小时，则有：

(1)

所以：

tanφ3-tanφ2≈tanφ2-tanφ1≈0

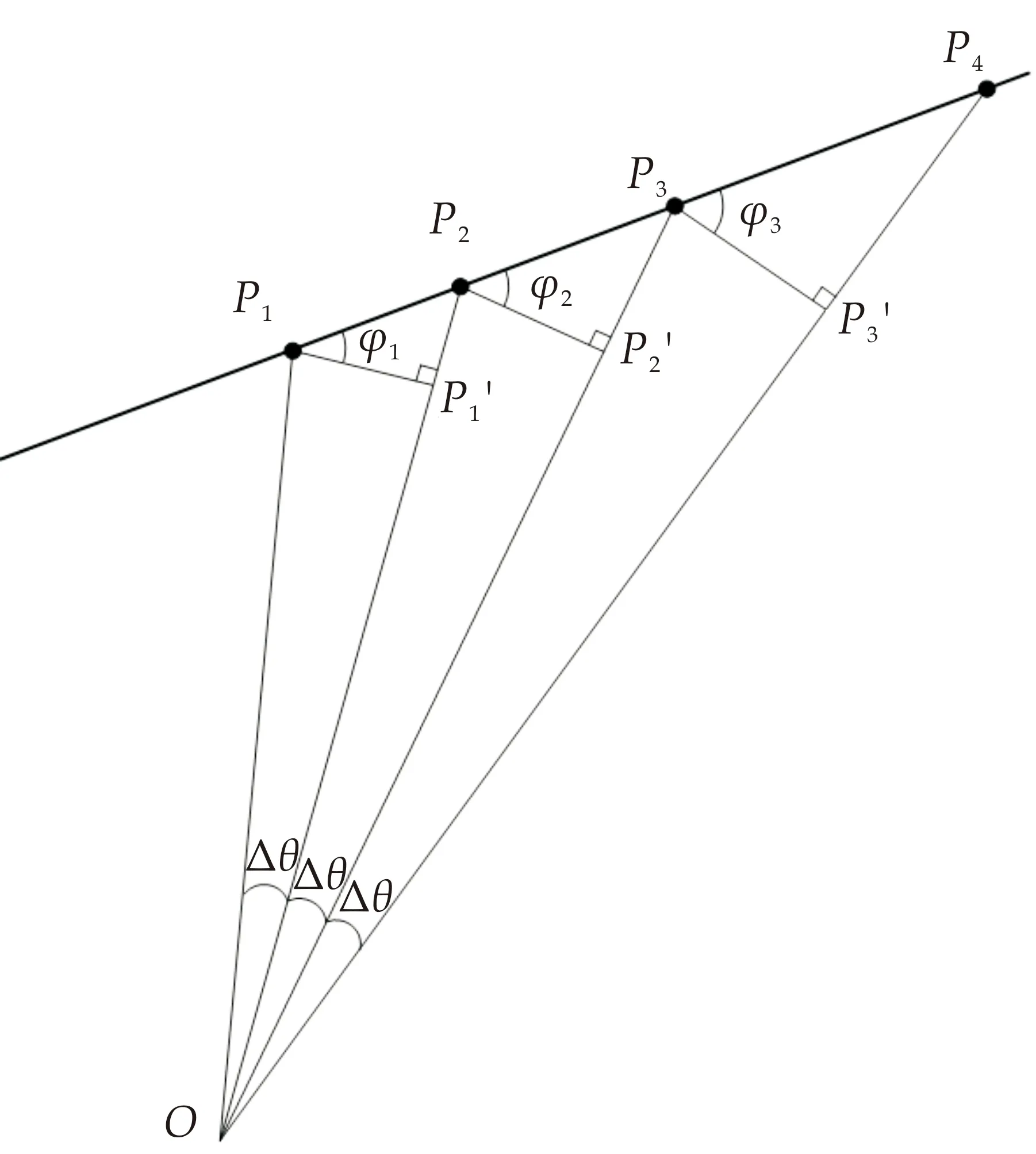
图1 扫描点示意图

由此可得，当相邻两点处的k值之差很小时，就认为该两点处于同一条直线上，否则该点为断点或角点.利用此方法即可对激光雷达扫描点进行分割，分割后采用最小二乘法对直线进行拟合，再通过拟合后的直线交点对角点进行更新，最后获取特征点点集PF[11].

PF={(xi,yi,fi,ki,li,wi),i=1,2,…,n}

(2)

式(2)中：xi,yi为特征点在当前坐标系下的坐标；fi为特征点的类型，1为角点特征，2为线段特征(线段特征以线段中点作为特征点)；ki为特征点的夹角或斜率，如果是角点特征，则其为角点相对应两条直线的夹角；如果是线段特征，则其为该线段在当前坐标系下的斜率；li为线段特征的长度，如果为角点特征，则该值为0；wi为该特征点的权重系数.对于角点特征，如果组成该角点的两条边均较长，则其权重系数较大，相反则较小；对于线段特征，如果该线段两端均为角点特征，或线段长度较长时，其权重系数较大，相反则较小.本算法为了提高匹配的精度，剔除掉了权重系数较小的特征点.

2 特征点匹配

ICP算法需要分别在待匹配的当前帧点云P和目标帧点云Q中，按照一定的约束条件，计算两点间的距离，找到最邻近点(pi,qj)，但是由于点云中点数较多，计算复杂度高、计算量大.经过特征提取后的特征点数将远少于原始点云中的点数，减少了运算量，而且通过特征点的特征值之间的差异可以进一步加快匹配的速度.

在提取的特征点中，角点特征相对较精确，但是一般数量较少，如果仅使用角点特征进行匹配则会造成较大的误差，甚至是无法匹配的情况.由于激光雷达扫描的特点，在不同位置对同一物体进行扫描时可能因为相互的遮挡而导致提取的线段特征不同，特别是在线段长度方面，所以线段特征点也很难直接进行匹配.因此，本算法考虑了特征点以上因素，提出了通过特征点计算两条线段之间的距离来进行匹配的方法.

2.1 计算对应特征点集

假设当前帧点云提取的特征点集为PF，共有n个特征点，其中角点特征nc个，角点特征点集记为PFc，线段特征nl个，线段特征点集记为PFl；目标帧点云提取的特征点集为QF，共有m个特征点，其中角点特征mc个，角点特征点集记为QFc， 线段特征ml个，线段特征点集记为QFl.

如果PF中的第i点fpi=1，即pi点为角点特征时，在QFc点集中，依次计算Δki=|kpi-kqj|.当Δki大于设定的阈值，则说明角点qj与pi的夹角相差较大，不可能成为对应点，并将其从QFc点集中删除，构成新点集QFc′，最后依次计算pi与QFc′中各点的距离，将距离最近点作为pi的对应点.

如果PF中的第i点fpi=2，即pi点为线段特征时，在QFl点集中，依次计算Δki=|kpi-kqj|.当Δki大于设定的阈值，则说明线段特征点qj与pi的斜率相差较大，不可能成为对应点，并将其从QFl点集中删除，构成新点集QFl′，最后依次计算pi到QFl′中各特征点对应线段间的距离，将距离最近的线段中点qj所在的线段Lq作为pi所在线段的对应线段.如图2所示，pc为特征线段Lp的中点，坐标为(xp,yp)，qc为特征线段Lq的中点，坐标为(xq,yq)，线段pcqc′的长度即为特征线段Lp与Lq之间的距离，qc′为pc的对应点.在匹配过程中，随着Lq与Lp之间位置的变化，qc′在线段Lq上的位置也是变化的.

最终得到对应点集{Pc,Qc,fc}为：

{(pcix,pciy,kpi,lpi),(qcix,qciy,kqi),fci,i=

1,2,…}

(3)

式(3)中：pcix,pciy,qcix,qciy分别为pci点和qci点在其坐标系中的坐标；fci为特征类型，如为角点特征，kpi和kqi相等，表示该角点夹角的正切值，如为线段特征，kpi和kqi分别特征线段Lpi和Lqi对应的斜率；lpi为线段特征Lpi的长度(如为角点特征，则该值为0).

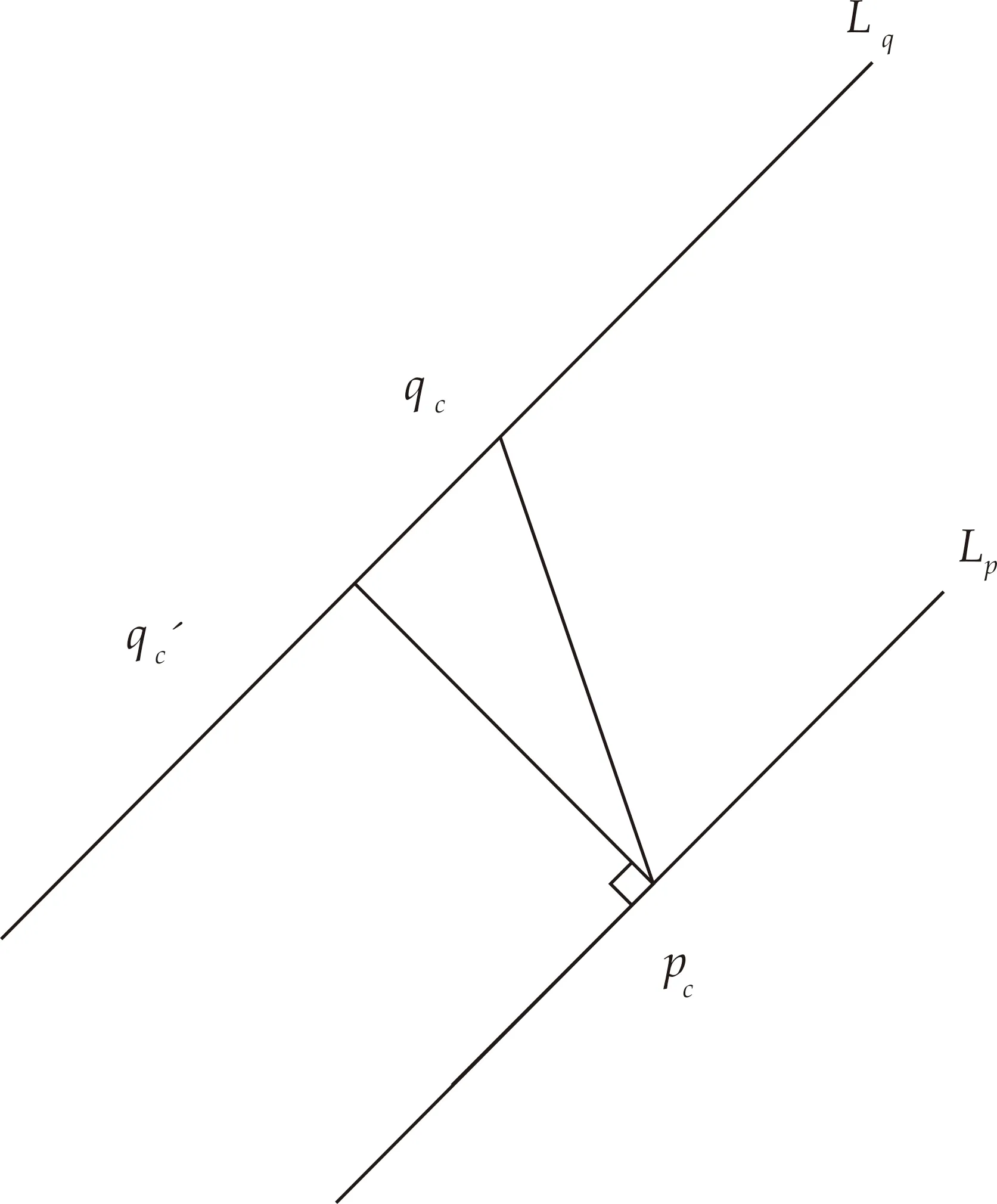
图2 特征线段间距离示意图

2.2 点集变换矩阵的求解

根据ICP算法，对应点集{ai}和{bi}的刚体变换关系为：

a=Rb+T

(4)

式(4)中：R为旋转矩阵，Δφ表示两帧点集之间的旋转角度，T为平移向量，Δx，Δy分别表示两帧点集之间在x和y方向的位移.Ca和Cb分别为点集{ai}和{bi}对应的中心点.

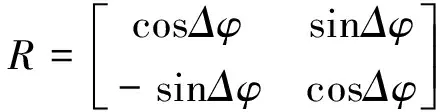
(5)

(6)

只要满足两帧点集中对应点间距离最小，即：

(7)

在对应点(Pci,Qci,fci)中，fci=1时，则直接将(pcix,pciy),(qcix,qciy)分别加入点集{ai}和{bi}中.fci=2时，该特征为线段特征，如果仅使用一个点进行匹配，则无法消除旋转因素产生的误差，如图3所示.因此，本算法使用当前帧中特征线段Lpi的两个端点pli和pri，分别求出在目标帧中对应线段Lqi上的两个对应点qli和qri，以此进行匹配来消除旋转产生的误差.

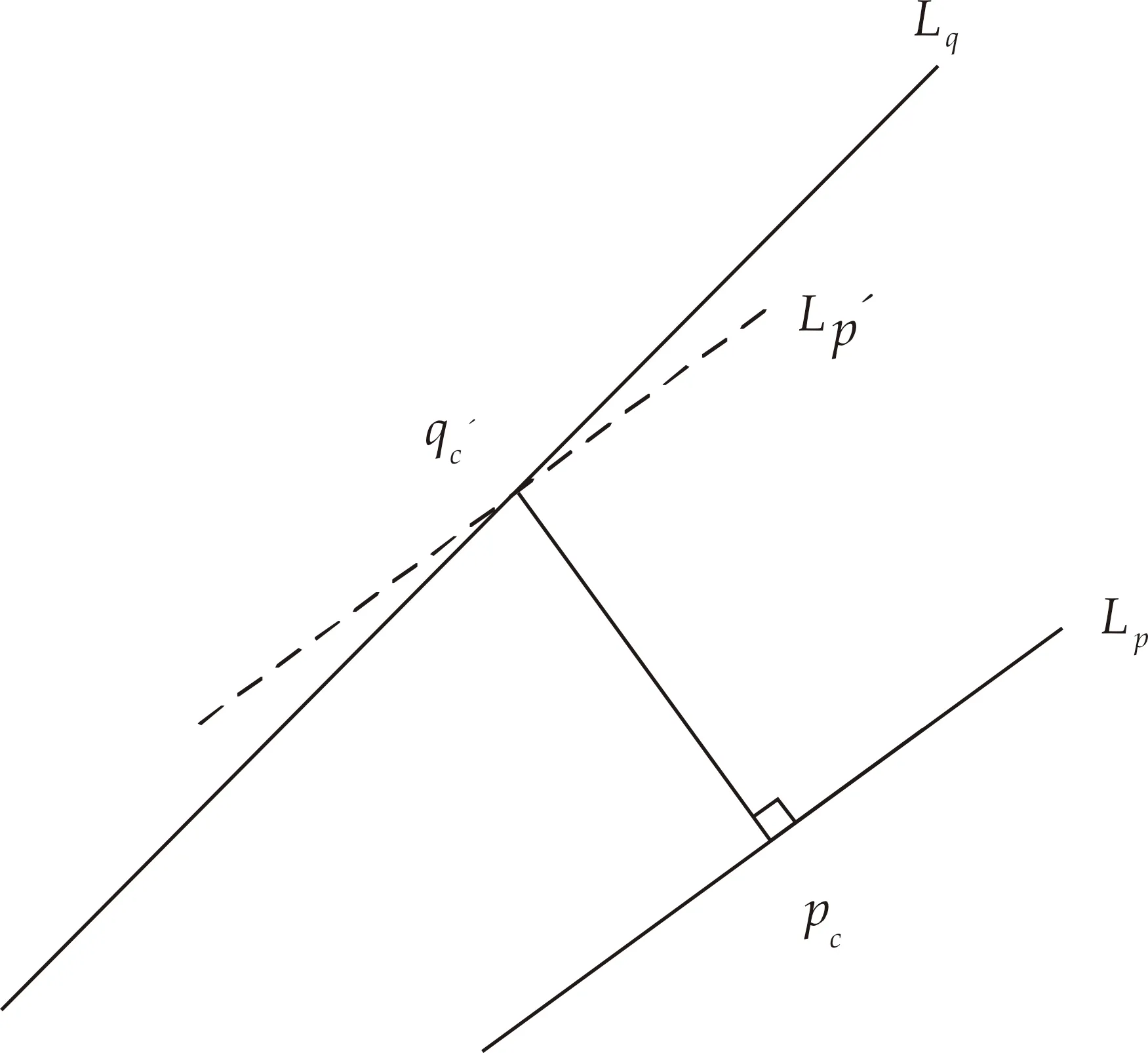
图3 特征线段单点匹配示意图

如图4所示，由Pci点分别求出Lpi的两个端点坐标(plix,pliy)和(prix,priy)，然后分别由pli和pri向线段Lqi作垂线，并根据Qci求得交点qli和qri的坐标(qlix,qliy)和(qrix,qriy)，并将其分别加入点集{ai}和{bi}中.

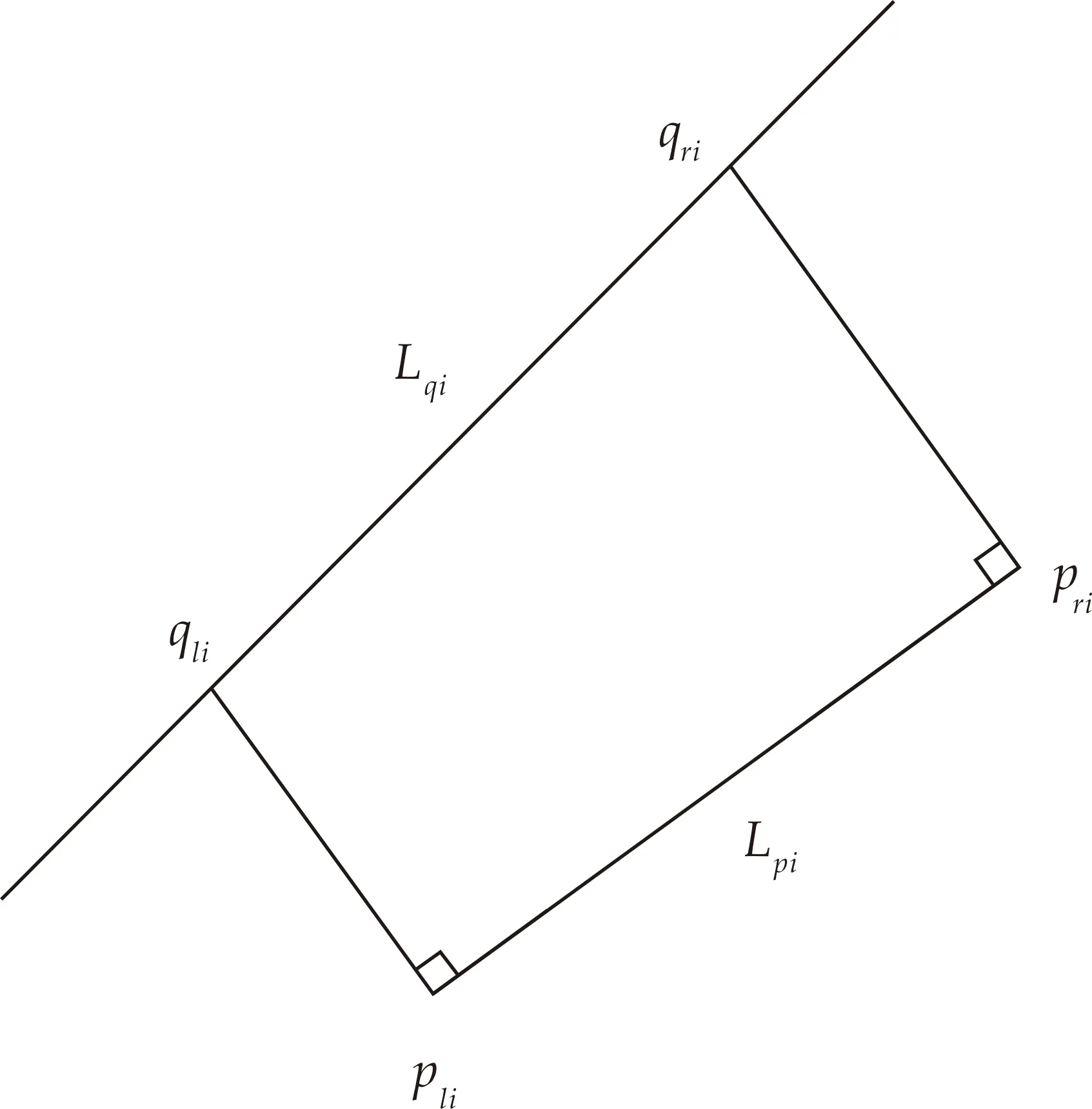
图4 特征线段两点匹配示意图

在求解参数R和T时，先将点集{ai}和{bi}进行Procrustes正则化处理，其中：

匹配误差err即为ai和bi中对应点两点间距离之和.

在旋转矩阵中：

(8)

将Δφ带入式(5)和式(6)可得R′和T′.

由式(4)可得：

(9)

R=R′R

T=R′T+T′

3 实验及结果分析

实验数据来自Cartographer ROS提供的德意志博物馆Deutsches Museum的2D激光SLAM数据集[13].算法使用Matlab2014b，计算机CPU为Intel Core i5-6300U，内存8G.为了验证本算法的正确性，从数据集中选取了第61帧与第62帧数据进行匹配.两帧激光雷达数据经过特征提取和匹配后的共有13组对应点，其中角点特征2组，线段特征11组.如图5所示，*表示61帧(目标帧)特征点，·表示62帧(当前帧)特征点，为了表示方便，分别用小写字母和大写字母对线段特征和角点特征进行了编号.

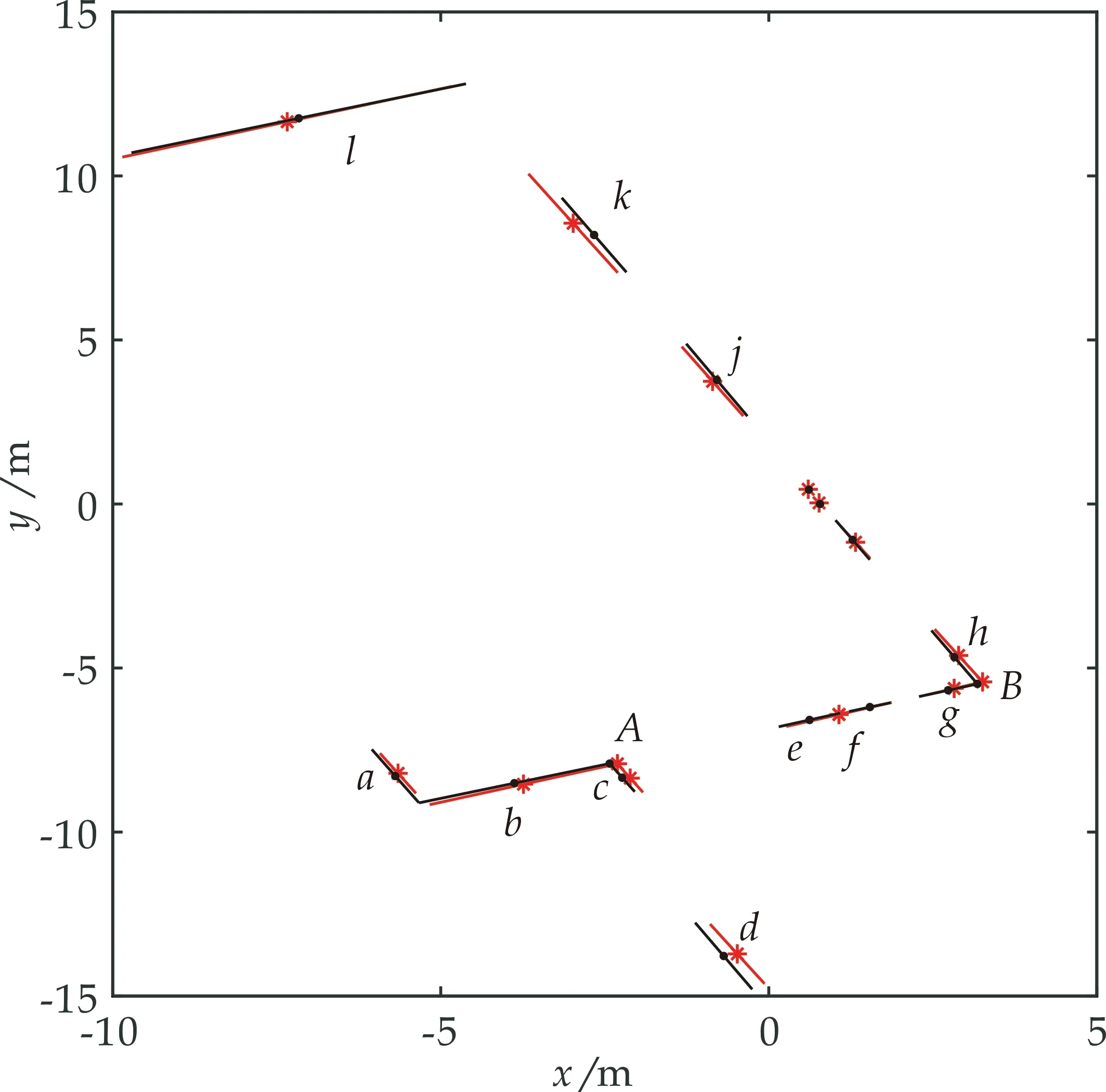
图5 特征点位置示意图

为了验证本算法的有效性和匹配精度，将目标帧与当前帧中的点集分别按本算法、迭代最近点算法(ICP)和栅格相关性方法(CSM)获得两帧数据间的位移和转角，并计算出相应算法匹配后的点集，然后，再将三个匹配后的点集按照前述特征点提取的方法提取角点和线段特征进行对比，如表1所示.表1的距离是匹配后点集提取的特征点与目标帧点集提取的特征点之间的距离，其中角点特征为两点间距离，线段特征则按前述方法计算两线段间距离.图6和图7为局部放大后，各算法计算的匹配后点集提取的特征与目标帧点集提取的特征之间的位置关系.

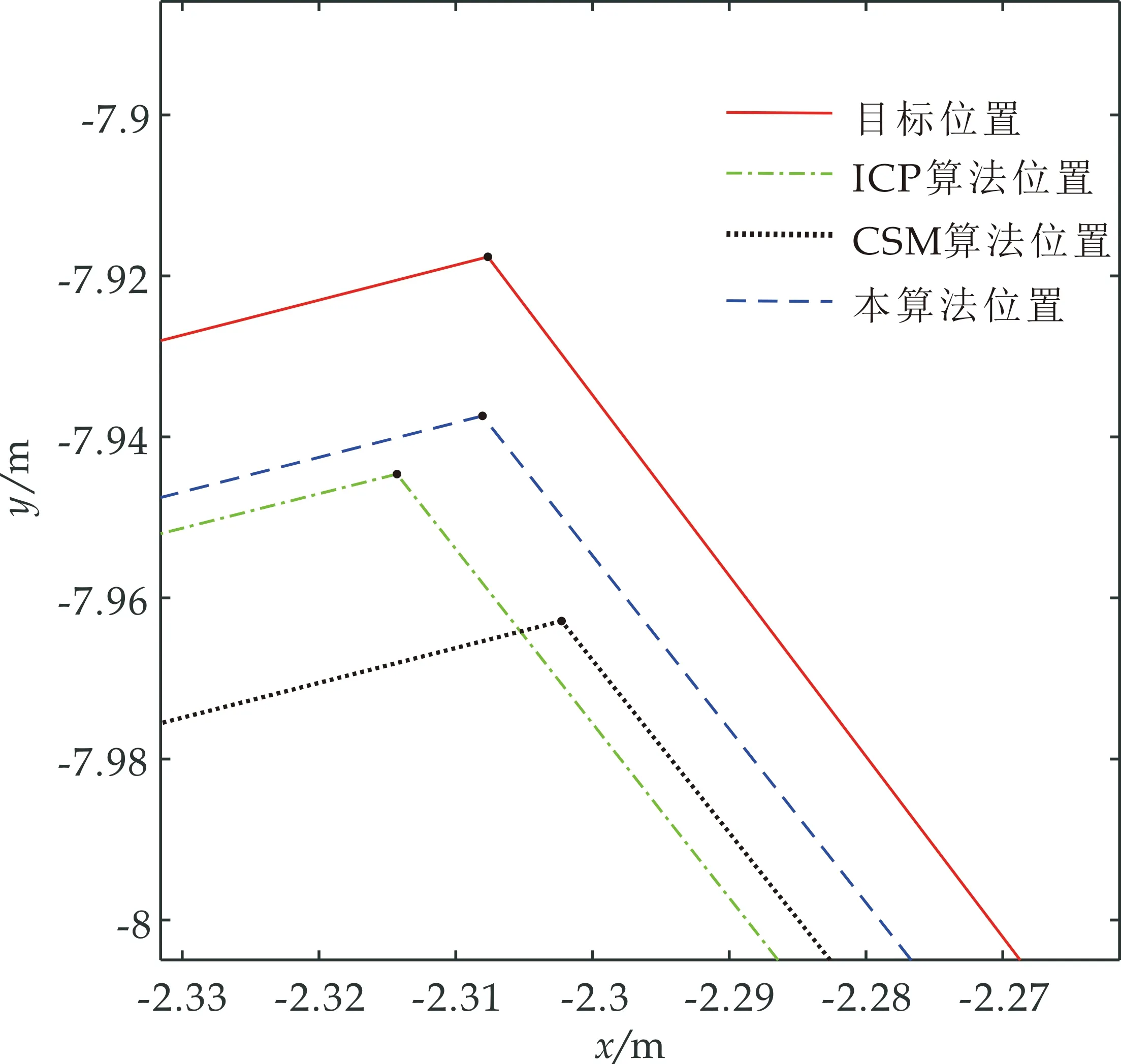
图6 匹配后角点A处放大图

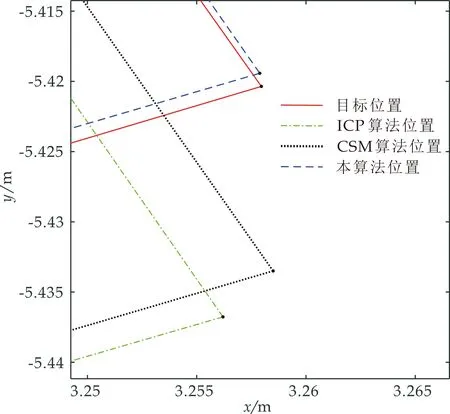
图7 匹配后角点B处放大图

根据表1中的数据可以发现，本算法的匹配精度较好，13个特征点匹配后与目标位置之间的距离范围为[0.001,0.022]，平均值为0.009，均方差为0.006，而采用ICP算法匹配后的特征点与目标位置之间的距离范围为[0.002,0.042]，平均值为0.014，均方差为0.012,采用CSM算法匹配后的特征点与目标位置之间的距离范围为[0.003,0.046]，平均值为0.016，均方差为0.014.

同时，数据集中选取了从60帧开始的连续11帧数据，进行相邻两帧数据的匹配，用匹配后特征点的位置与目标位置之间的距离作为考察的指标，并对三种算法的计算效率进行了对比.表2中分别给出了每次匹配后，所有对应特征点距离的平均值和最大值，以及每次匹配计算所消耗的时间.其中距离是指在一次匹配时，由算法计算出的位置与目标位置之间的距离.

由表2中数据可以发现，本算法在连续数据帧间进行匹配时，仍然具有较好的精度，距离的平均值范围为[0.005,0.024]，而ICP算法得到的距离平均值范围为[0.013,0.057]，CSM算法得到的距离平均值范围为[0.009,0.025].在计算效率方面，三种算法的平均耗时分别为18.91 ms、124.02 ms和26.65 ms，所以本算法连续10帧的匹配结果，在平均值、最大值和计算耗时三方面均优于ICP和CSM算法.

为了进一步验证本算法在实际应用中有效性，选取某楼端侧梯形平台为测试对象，该平台几何尺寸使用卷尺测量后如图8所示[11].使用自主制作的移动机器人在测试平台随机选取了10个点进行扫描获取10帧扫描数据，其中激光雷达选用SLAMTEC公司的RPLIDAR A2型.将其中任意一帧数据作为目标帧(本实验中使用第7帧)，其余帧数据依次按照本算法对其进行匹配，并将匹配结果绘制于同一坐标系中，如图9所示(由于各数据帧间位移较大，所以匹配前使用了里程计数据进行粗定位).图9中各交点或端点坐标为其附近各条线段上对应点坐标的平均值.

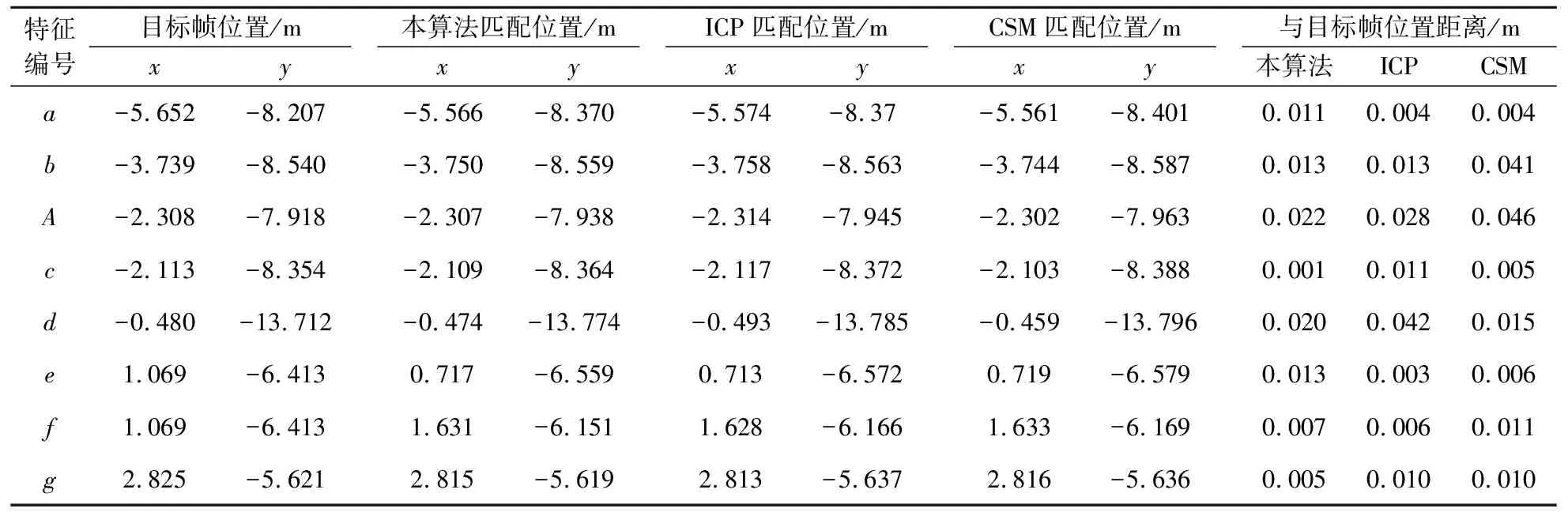
表1 61帧与62帧匹配结果本算法与ICP和CSM对比

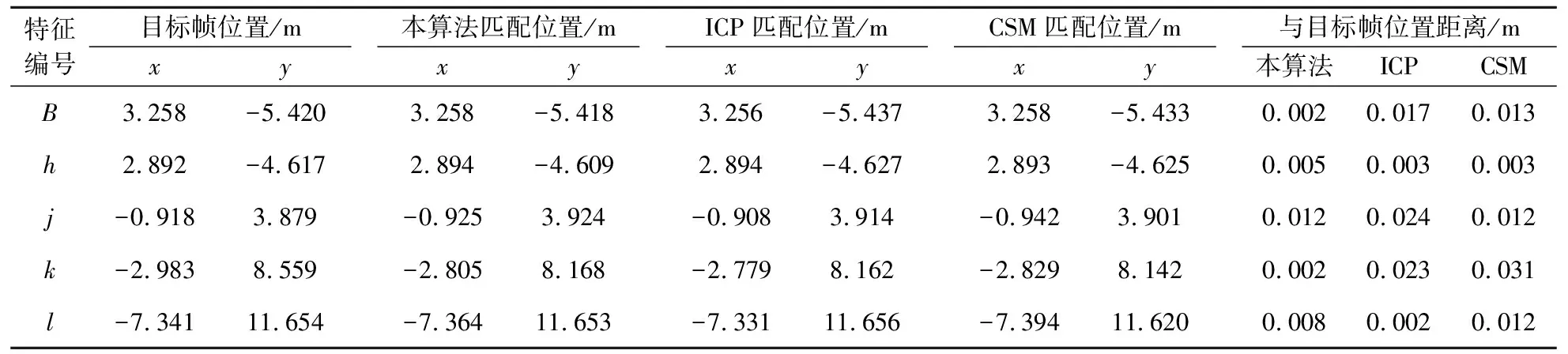
续表1

图10和图11分别为ICP算法和CSM算法匹配后的结果.由图9可以发现，各帧中提取的线段均存在误差，部分线段不完整，但是经过匹配后，大部分线段的位置波动范围较小，形状基本与平台一致，相较于ICP和CSM算法匹配效果更好.

最后，为了直观评价匹配结果，分别用三种算法求出相应线段两点间长度与测量值进行对比，结果如表3所示.其中相对差值按式(10)计算.

(10)

表2 本算法连续帧匹配结果及计算效率与ICP和CSM对比

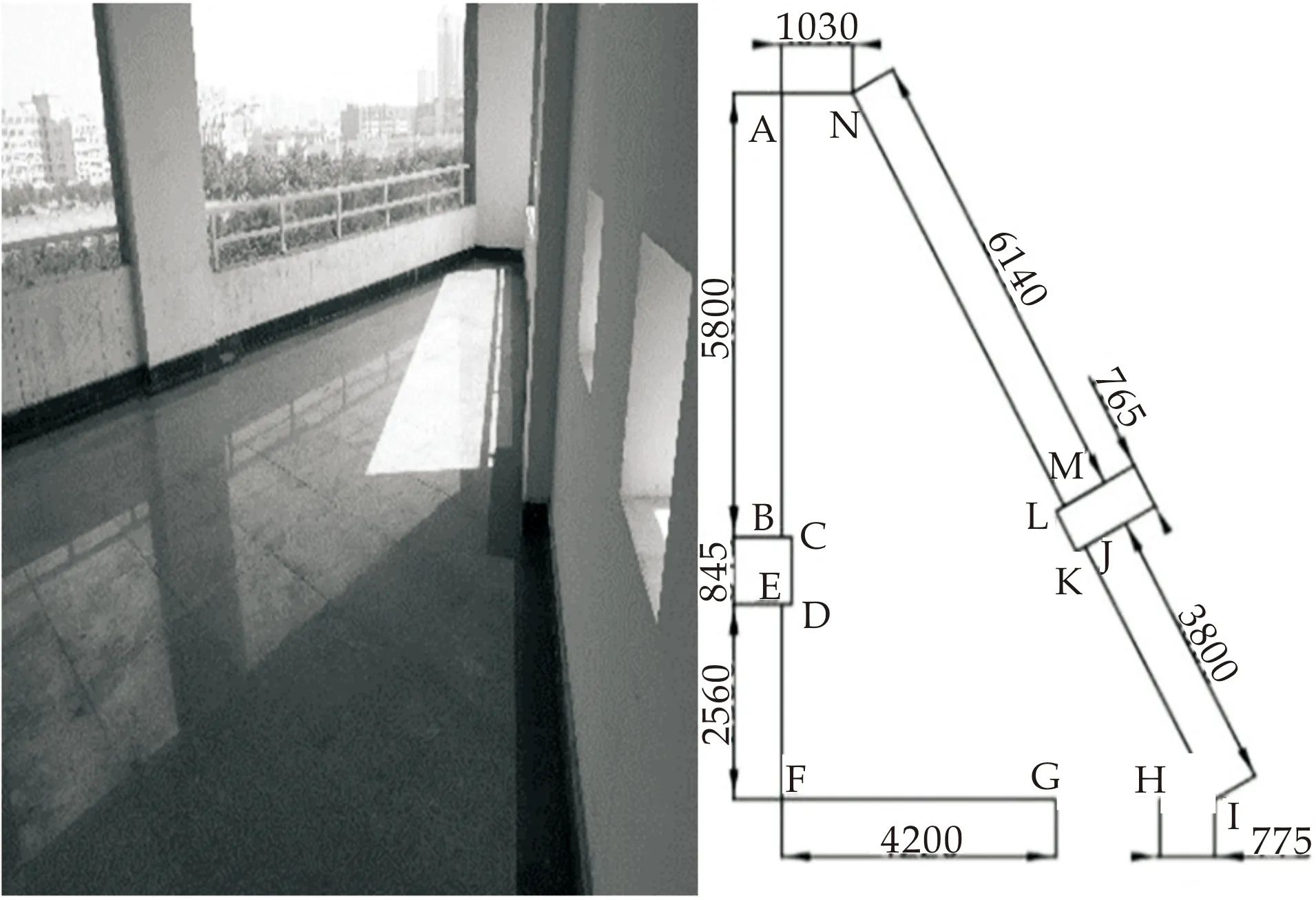
图8 实验测试平台

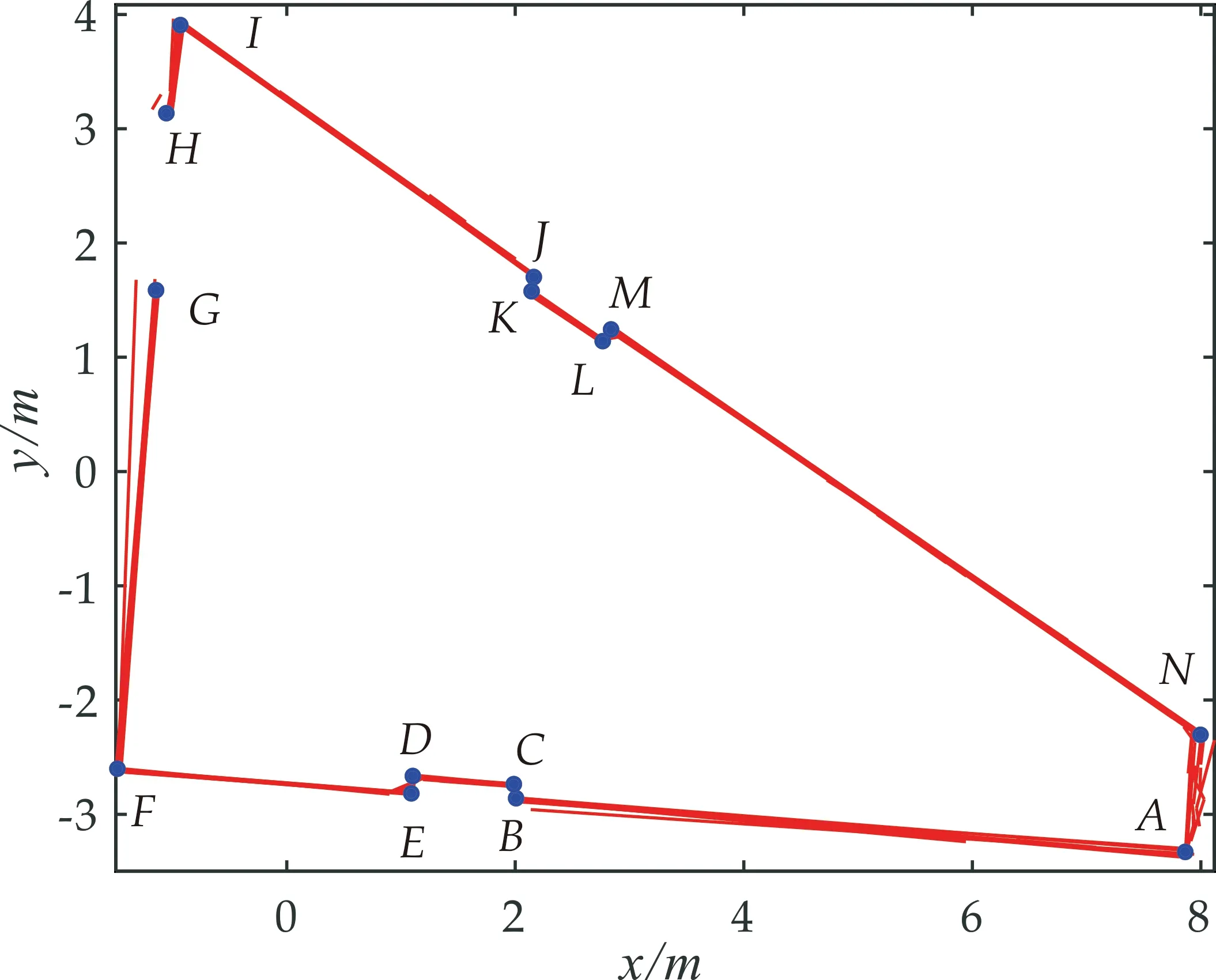
图9 本算法匹配后结果

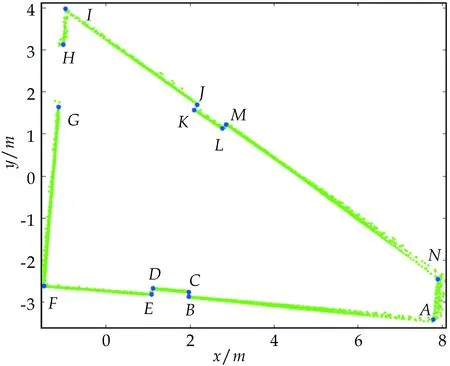
图10 ICP算法匹配后结果

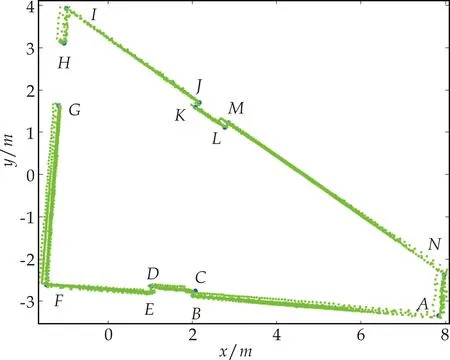
图11 CSM算法匹配后结果

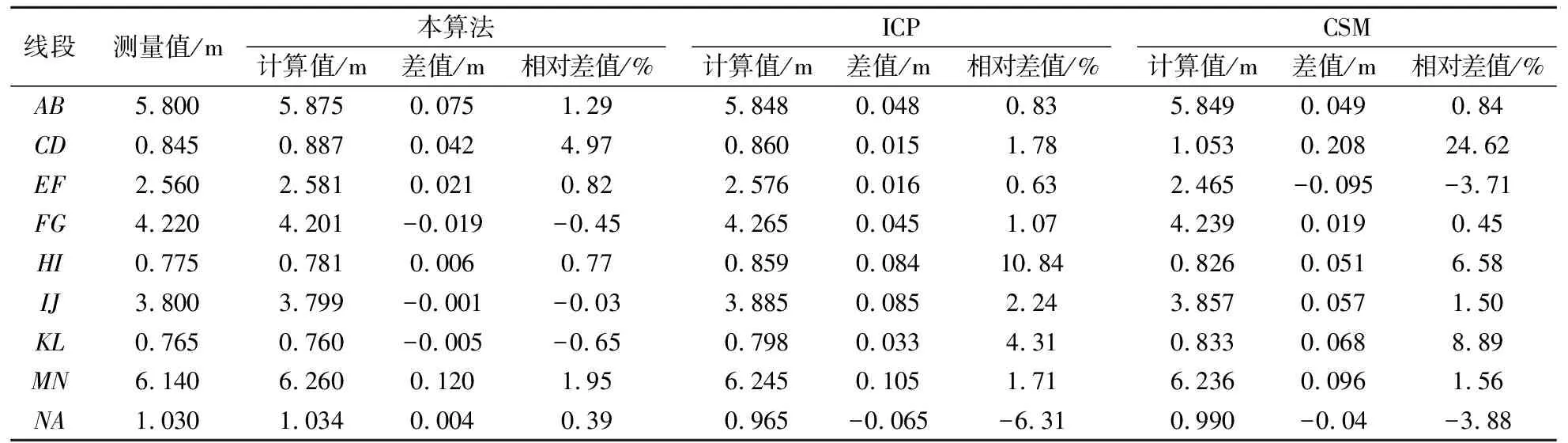
表3 匹配后各线段计算值与测量值对比

4 结论

本文提出了一种针对激光雷达扫描数据进行匹配的算法，该算法先通过计算相邻点斜率差将扫描点集进行分割和特征提取，然后按照ICP算法的原理，将提取的特征点进行匹配.由于该算法采用特征值进行匹配，降低了初值的敏感性，并且通过匹配特征点的类型和特征值，加快了匹配速度，提高了匹配的准确性.同时，本算法在进行线段特征点匹配时，使用线段间的距离代替两特征点间的距离，进一步保证了算法的准确性和精度.经过实验验证，本算法的匹配效果较好，且在同等条件下优于ICP和CSM算法，但本算法仅需匹配少数特征点，因此，计算量与CSM和ICP等算法相比有所下降.

本算法给出了提取的特征点可靠性判断依据和权重，在此基础上，匹配时可以加入特征点的权重系数，从而进一步提高匹配的精度和效率.