静态推靠式导向翼肋陷入井壁风险分析

史玉才 岳德胜 张德军 付成林 张文盛 常迪 邵光昊

1. 中国石油大学(华东)；2. 非常规油气开发重点实验室(中国石油大学华东分校)；3. 中国石油川庆钻探有限公司；4. 中国石化江苏油田分公司石油工程技术研究院

旋转导向钻井系统(RSS)是目前最先进和最有代表性的导向钻井系统，也是高难度定向钻井作业的核心装备和必备利器。与滑动导向钻井系统相比，旋转导向钻井系统可在钻柱旋转钻进过程中灵活调整井斜角和方位角，可大幅度提高钻井速度和钻井安全性，其轨迹控制精度也非常高［1-3］。国内从20 世纪90 年代中期开始研制旋转导向钻井系统，目前已成功研制出与Baker Hughes 公司Auto Trak 钻井系统类似的静态推靠式旋转导向钻井系统，部分国产系统已进入工业化应用［4-5］。

静态推靠式旋转导向钻井系统依靠导向翼肋推靠井壁来为钻头提供导向力［3,6］。现有导向翼肋多采用单柱塞铰接式结构，上端用销钉固定，下端由单柱塞施加推靠力［7］。理论研究和现场实践表明，单柱塞铰接式导向翼肋有可能导致井下复杂情况。例如，导向翼肋与井壁之间存在较大摩擦力，影响钻压传递效率和钻井速度［8-9］；当地层较软时导向翼肋还有可能陷入地层，影响造斜率和井眼轨迹调控精度［8-9］。国内在渤海油田、国外在墨西哥湾［10］、喀麦隆近海［11］、挪威南部［12］、泰国湾［13］等油田均出现过导向工具在软弱地层中造斜率不足、导向控制差等问题，这些地区地层的单轴抗压强度(UCS) 基本都位于6.89~13.79 MPa (1 000~2 000 psi)之间。

到目前为止，国内外对静态推靠式导向翼肋与井壁连续接触问题研究较少，难以为导向翼肋结构改进提供支持。鉴于此，笔者采用有限元软件对导向翼肋与井壁接触过程进行了模拟，探讨井壁的屈服情况，并分析了影响井壁破坏的因素，为避免导向翼肋陷入井壁提供理论支撑。

1 导向翼肋与井壁接触分析模型

借助有限元软件ABAQUS 的Explicit 模块对静态推靠铰接式导向翼肋与井壁的接触问题进行仿真模拟。Explicit 模块可以进行显式动态分析，适于求解复杂非线性动力学问题和准静态问题，对处理接触条件变化的高度非线性问题也非常有效［14-16］。

1.1 岩石破坏准则的选择

在研究岩石材料塑性变形阶段的屈服破坏特性时，最常用的岩石破坏准则是Mohr-Coulomb 准则和Drucker-Prager 准 则［17-18］。其 中，Drucker-Prager 准则不仅考虑了静水压力和中间主应力对岩石屈服失效过程的影响，克服了Mohr-Coulomb 准则的主要缺陷，还能反映剪切力引起的扩容，在国内外岩石力学数值分析和计算中得到广泛应用。

有限元软件ABAQUS 中，Drucker-Prager 准则包括线性、双曲线和指数函数3 种模型［18］。此处采用线性Drucker-Prager 准则来满足动态分析要求。目前岩石的内聚力、内摩擦角等参数大多是基于Mohr-Coulomb 准则，需要先转换至Drucker-Prager 准则，三维情况下转换方法如下。

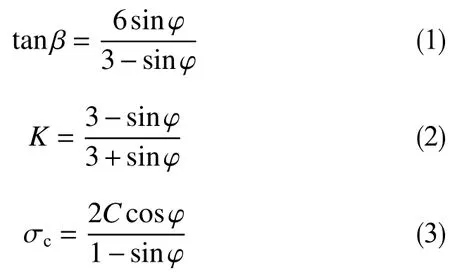
式中，β、K、σc分别为Drucker-Prager 准则对应的岩石内摩擦角(°)、流应变率、屈服强度(MPa)； φ、C分别为Mohr-Coulomb 准则对应的岩石内摩擦角(°)和岩石内聚力(MPa)。

1.2 导向翼肋与井壁的处理

单柱塞铰接式导向翼肋和井壁的几何模型见图1。考虑到所研究问题的对称性，选用一半井壁进行分析。以Ø216 mm 井眼为例，参照国内在研的旋转导向钻井工具，导向翼肋的曲率半径(工作面曲率半径)、弹性模量和泊松比分别取为107 mm、210 GPa 和0.3。导向翼肋和井壁的整体网格尺寸设为5 mm，井壁与翼肋的接触部分设为2 mm。

1.3 井壁接触应力分布规律

地层的弹性模量和泊松比分别取为1.5 GPa 和0.3，Mohr-Coulomb 准则下内摩擦角和内聚力分别为20°和1.5 MPa；导向翼肋与井壁之间的摩擦系数取0.3；在导向翼肋的凹面上施加20 kN 的垂直向下的推靠力，在销钉孔上施加固定约束(见图1b)。

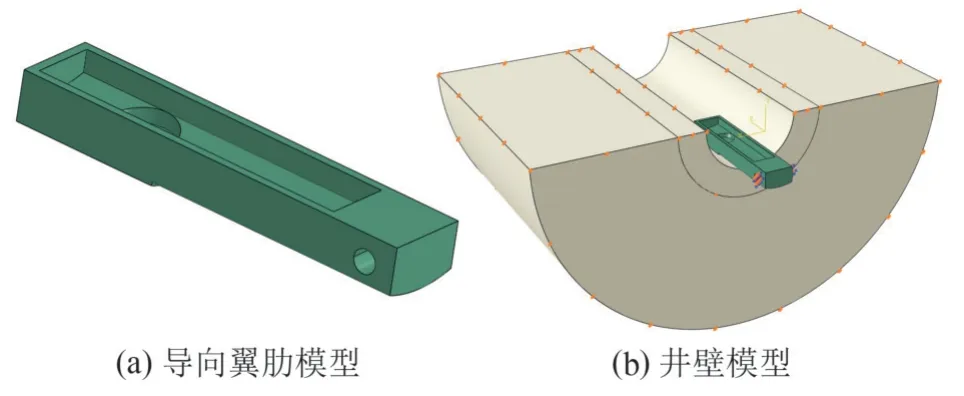
图 1 导向翼肋模型和井壁几何模型Fig. 1 Steering rib model and well wall geometric model

导向翼肋与井壁接触应力分布见图2，可以看出，单柱塞铰接式导向翼肋与井壁之间表现为角接触，接触应力分布不均匀；最大应力位于翼肋上端，在翼肋凹坑处接触应力也较大。

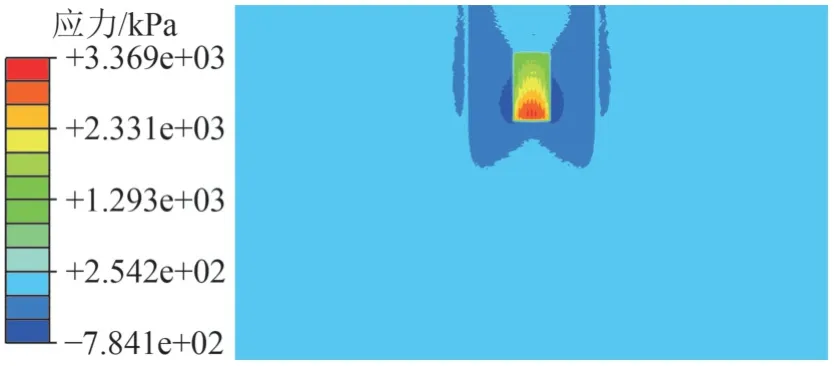
图 2 接触应力分布图Fig. 2 Distribution of contact stress

2 导向翼肋陷入井壁模拟分析方法

考虑导向翼肋有可能陷入井壁的情况，以疏松砂岩地层为例。通过查阅相关文献［19-20］，取井壁弹性模量1.5 GPa，泊松比0.3，内摩擦角20°，内聚力1.5 MPa，岩石屈服准则采用线性Drucker-Prager准则。导向翼肋与井壁间的摩擦系数取0.3。考虑到翼肋的运动状态，设置以下2 个载荷步：其中，第1 个分析步在翼肋的凹坑处施加竖直向下的30 kN的推靠力，时间为10 s；第2 个分析步对翼肋施加平行于井眼轴线的0.002 8 m/s 的线速度(相当于导向翼肋保持10 m/h 速度沿井壁向下滑动)，时间为30 s。当分析步加载完成时，井壁和导向翼肋整体变形及井壁的等效塑性应变如图3 所示。可以看出，井壁已经发生了塑性变形。

提取各时间点井壁的最大变形量和Mises 应力，绘制出井壁变形和Mises 应力随时间变化曲线，从图4 可以看出，在当前模拟计算条件下，推靠力加载完成后，井壁变形量很小；随着导向翼肋沿井眼轴线方向移动，井壁变形量随时间延长逐渐增大，导向翼肋逐渐开始陷入地层；之后，导向翼肋的陷入深度近似呈线性增加。

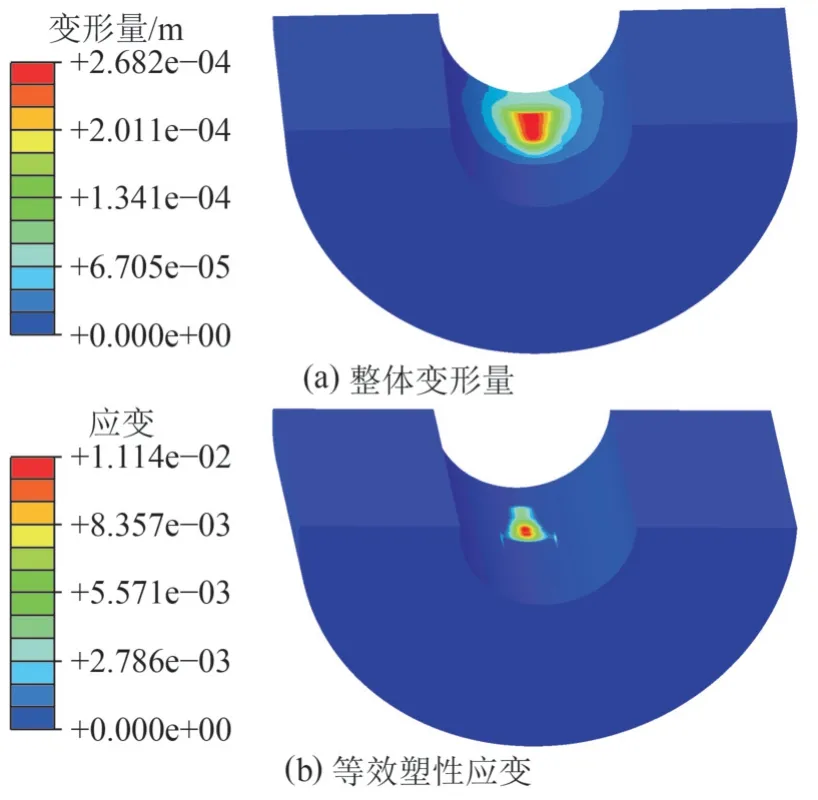
图 3 井壁变形和等效塑性应变Fig. 3 well wall deformation and equivalent plastic strain

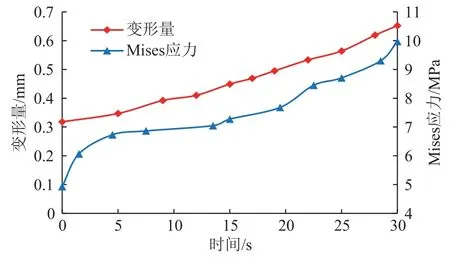
图 4 井壁变形量和Mises 应力随时间变化曲线Fig. 4 Variation of well deformation and Mises stress over time

3 导向翼肋陷入井壁的影响因素分析

理论与实践表明，在较软地层(如软泥岩、松散砂岩等)钻进时，导向翼肋有陷入井壁的可能。根据参考文献［19-20］，取软地层的弹性模量为0.5~2.5 GPa，内聚力为1~2 MPa，内摩擦角为15°~25°。对于导向翼肋的结构和工作参数，取翼肋的曲率半径为106~108 mm、推靠力为10~30 kN。根据以上参数范围，采用单因素轮换法，依次改变井壁岩石的弹性模量、内聚力、内摩擦角、推靠力和翼肋曲率半径的大小，分别研究井壁的破坏过程与各个因素之间的关系及其各自的影响规律。

3.1 岩石弹性模量的影响

取井壁岩石的内聚力为1.5 MPa，内摩擦角为20°，翼肋的曲率半径为107 mm、推靠力为30 kN，井壁岩石的弹性模量分别取0.5、1.5、3 GPa，得到井壁变形量随时间变化曲线如图5 所示，可以看出，井壁岩石的弹性模量对井壁变形有很大影响。当井壁岩石的弹性模量减小时，井壁初始变形(推靠力加载完成时的变形)会大大增加，井壁变形率也会增加，导向翼肋会陷入井壁中；当弹性模量增大到一定程度时，井壁变形并不随导向翼肋的移动时间而增大，证明此时导向翼肋不会陷入井壁。由此可见，在岩石弹性模量较小的地层中钻进时，导向翼肋会陷入井壁。

图 5 不同弹性模量下井壁变形量变化曲线Fig. 5 Variation curve of well wall deformation under different elastic moduli

3.2 岩石内聚力的影响

取井壁岩石的弹性模量1.5 GPa，内摩擦角20°，翼肋的曲率半径为107 mm、推靠力30 kN，分别取井壁岩石的内聚力为1、1.5、2 MPa，得到井壁变形量随时间变化曲线，如图6 所示。

图 6 不同内聚力下井壁变形量变化曲线Fig. 6 Variation curve of well wall deformation underdifferent internal cohesions

由图6 可以看出，井壁岩石的内聚力对井壁的破坏速率具有较大影响。在翼肋陷入井壁的情况下，改变井壁岩石的内聚力对井壁初始变形量并无影响，但当内聚力降低时，井壁变形速率会明显增加，翼肋将会更快地陷入井壁。当井壁岩石的内聚力增大到一定程度时，翼肋不会再陷入井壁。

3.3 岩石内摩擦角的影响

取井壁岩石的弹性模量1.5 GPa，内聚力1.5 MPa，导向翼肋的曲率半径107 mm、推靠力30 kN，分别取井壁岩石的内摩擦角为15°、20°和25°，得到井壁变形量随时间变化曲线，如图7 所示。

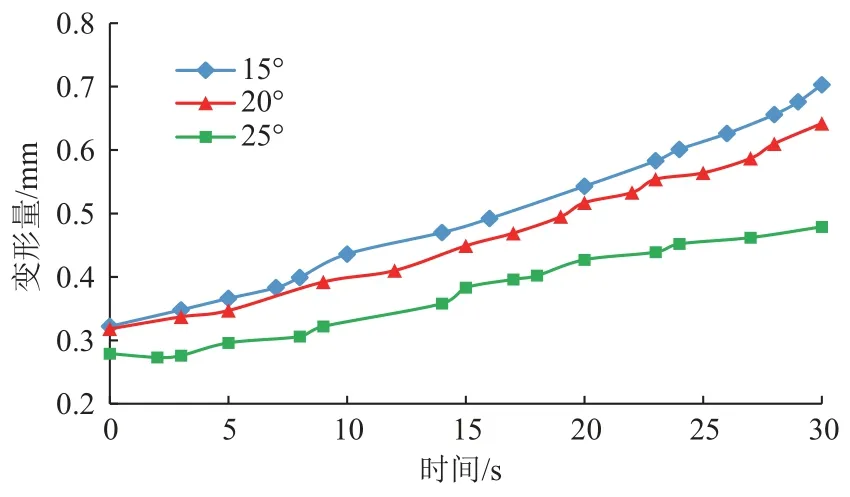
图 7 不同内摩擦角时井壁变形量变化曲线Fig. 7 Variation curve of well wall deformation underdifferent internal friction angles

由图7 可以看出，井壁岩石的内摩擦角对导向翼肋陷入井壁影响与内聚力影响大致相同。由于内聚力和内摩擦角都是通过影响岩石的屈服应力来影响井壁变形量，二者对井壁变形的影响规律基本相同，但是岩石的屈服应力受内聚力的影响更大一些，内摩擦角的影响程度要小得多。

3.4 推靠力的影响

根据现场经验和之前的研究成果，推靠力对导向翼肋与井壁间的接触应力、导向翼肋是否陷入井壁有明显影响［7］。取井壁岩石的弹性模量1.5 GPa，内聚力1.5 MPa，内摩擦角20°，翼肋曲率半径107 mm，分别取推靠力10、20、30 kN，得到井壁变形量随时间变化曲线，如图8 所示。

图 8 不同推靠力下井壁变形量变化曲线Fig. 8 Variation curve of well wall deformation under different thrust forces

由图8 可以看出，当推靠力减小到20 kN 时，井壁变形量基本上不再随运动时间增加而增大，即导向翼肋不再会陷入井壁。因此，当推靠力减小到一定程度时，导向翼肋将不再陷入地层。

3.5 导向翼肋曲率半径的影响

取井壁弹性模量1.5 GPa，内聚力1.5 MPa，内摩擦角20°，推靠力30 kN，分别取导向翼肋曲率半径106、107、108 mm，得到井壁变形量随时间变化曲线如图9 所示，可以看出，当导向翼肋的曲率半径减小时，翼肋与井壁的接触面积将减小，井壁变形率将大大增加，导向翼肋将更快地陷入井壁；当导向翼肋的曲率半径增大到一定程度时，翼肋便不会吃入地层。另外，当导向翼肋的曲率半径超过井筒半径时，井壁的变形会不断增大，一段时间后井壁会出现破裂现象。因此，若要降低翼肋陷入井壁的风险，应使翼肋的曲率半径尽可能地接近井眼半径。

图 9 不同翼肋曲率半径下井壁变形量的变化曲线Fig. 9 Variation curve of well wall deformation under different rib curvature radii

4 避免导向翼肋陷入井壁对策分析

从上述分析可知，现有单柱塞铰接式导向翼肋在软地层中陷入井壁风险较高。现从以下3 个方面给出可避免导向翼肋陷入井壁的对策。

(1)改进导向翼肋结构，设法增大导向翼肋与井壁的接触面积。第1 种方法是优化导向翼肋的曲率半径，使翼肋的曲率半径尽可能地接近井眼半径。第2 种方法是采用双柱塞平推工作方式，将井壁与导向翼肋之间的接触类型从角接触改为平行接触。据文献报道，Baker Hughes 公司新型旋转导向钻井系统已采用双柱塞平推式导向翼肋，可有效防止导向翼肋陷入软地层，也有助于提高造斜率［21］。

(2)适当减小导向翼肋的推靠力。对于静态推靠式旋转导向钻井系统来说，整体增大或减小3 个导向翼肋的推靠力并不会降低导向力［6］。钻进软地层时，当对造斜率要求不高时可以适当减小推靠力。比如，66%和33%导向力情况下可以整体减小3 个推靠力，这样既保持导向合力的大小和方向不变，也有助于降低导向翼肋陷入井壁风险。

(3)做好地层适应性评价与筛选。上文模拟分析表明，导向翼肋的结构及工作参数确定之后，井壁岩石的力学性能决定了导向翼肋是否会陷入井壁。在钻前取全取准待钻地层的岩石力学参数，做好对不同结构导向翼肋的地层适应性评价，然后有针对性调整导向翼肋结构及工作参数，将能够大大降低导向翼肋陷入软地层风险。

5 结论

(1)现有的单柱塞铰接式导向翼肋与井壁为角接触，接触面积较小，导致接触应力分布不均匀，最大应力位于导向翼肋的上端，在导向翼肋的凹坑处接触应力也有明显的增大。

(2)在较软地层(如软泥岩、松散砂岩等) 中钻进时，随着导向翼肋的运动，井壁的变形量逐渐增大，导向翼肋会陷入地层中。

(3)井壁岩石的弹性模量和内聚力对井壁变形有很大影响。当井壁岩石的弹性模量增大到一定程度时，井壁变形不随导向翼肋运动时间而增大；推靠力对导向翼肋是否陷入井壁有很大影响，适当降低推靠力可以降低导向翼肋陷入井壁风险。

(4)改进导向翼肋结构(采用双柱塞平推工作方式、使导向翼肋的曲率半径尽量接近井筒半径)、适当减小导向翼肋的推靠力、做好地层适应性评价与筛选等，均有助于降低导向翼肋陷入井壁风险。