一种改进的无线传感器网络节点定位算法研究*

（中国人民解放军91388部队 湛江 524022）

1 引言

文献［7］提出了一种基于移动锚节点的定位方法，该方法根据距离未知节点最近的位置RSSI值信号最强，通过锚节点的直线轨迹与未知节点的圆形通信区域相交所得的两弦，由两弦的中垂线交点实现未知节点坐标求解，但是实际使用中未知节点的通信区域不一定呈理想圆形，引入加权因子求解得到弦的中点不一定是距离未知节点最近的点，从而导致误差的产生。

文献［8］提出了一种基于RSSI值的锚节点测量方法，该方法通过构建RSSI值与相对距离的多项式方程实现未知节点最近处的坐标位置求解，能较好避免文献［7］算法的缺陷。该算法不足之处是只采用运动轨迹上两个点的坐标值实现对锚节点直线轨迹方程的求解，将轨迹上某一位置点作为参考节点实现RSSI值方程的拟合求解，忽视了位置数据中的异常值［9］及GNSS系统的定位偏差［10］对求解的影响，该方法极有可能对未知节点坐标的解算带来极大的误差。

本文在文献［8］的基础上提出了一种改进的无线传感器节点定位算法。该算法中，锚节点在未知节点的通信区域内做折线运动，处于静止状态的未知节点获取到锚节点广播的位置数据和该点位的RSSI值，通过3σ准则，对位置数据中的异常值进行剔除；采用一元线性回归对经过异常值处理的位置数据集进行拟合处理，构建了基于折线交点的RSSI多项式模型，通过解算确定未知点在锚节点轨迹上的垂线，由两条垂线的交点求解出未知节点的位置。

2 系统模型

2.1 RSSI值模型

本文采用无线传感器网络中应用较为广泛的Shanowing模型［11～12］，即发射点距离d处的 RSSI值由下面的式（1）和（2）得出：

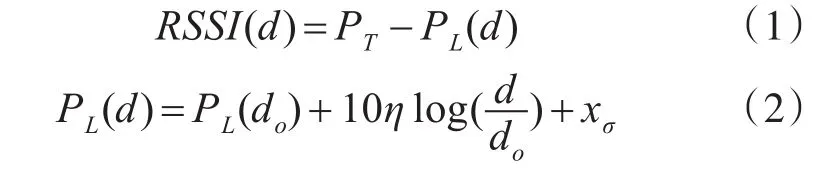
PT是信号发射功率；PL(do)是信号在参考距离(do)处的路径传播损失，do通常取值为1m；η是路径衰减因子，取值范围为2～5；xσ是服从高斯分布的随机变量，其均值为0，标准差的取值范围为4～10。

2.2 折线运动模型

为了便于未知节点坐标的求解，本文制定了锚节点的折线运动模型，具体叙述如下。

论做人地道，香娭毑在白家湾几十年，还真是没留话柄让人说。平日里，不管是谁，你从她家屋门口过，她总是热情地同你打招呼，你进来糯（坐）啦！呷拿（茶）啦！一口家乡话十分悦耳动听。她泡的姜盐茶和芝麻豆子茶还真是好呷，让人呷了一盅又一盅，舍不得放下盅哩。只可惜生不逢时，若放在当年乾隆爷下江南，呷了她的茶，这茶一定会成为贡品。大伢细崽去了她家，更讨她喜欢，她会变戏法似的，一会儿给你拿颗糖，一会儿抓把炸得透香的红薯片放到你手上，让你觉得像过年。白家湾无论大人还是细伢子，有事冇事都喜欢往她家拱。

如图1所示，未知节点U处于静止状态，虚线为U的通信半径，K为具备定位功能（即安装有GNSS系统）的锚节点，其接到未知节点的定位需求以后规划路径，在U的通信区域内做折线运动，并周期性地广播位置信息。未知节点接收到其广播的位置信息并获取其在该位置的RSSI值。

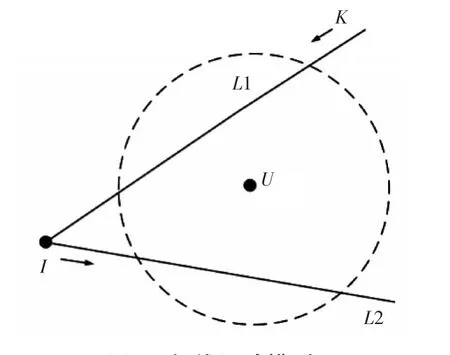
图1 折线运动模型

2.3 基于一元线性回归的直线轨迹方程求解模型

如图1示，锚节点在直线轨迹L1和L2上运动时，未知节点将会分别获得一组具有线性关系的位置数据集 (xi，yi)(i=1，2，...，n)，设直线轨迹方程为

为获得该组数据的最佳线性关系，一元线性回归中常采用最小二乘准则对数据进行处理，即参数a和b的值可以由式（4）和式（5）［13］得出：

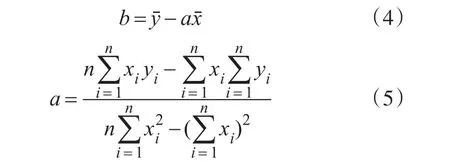
当测量数据中存在有异常值时，由于异常值会对回归效果产生扭曲，采用最小二乘准则并不能获得最佳线性关系。为减小测量数据中异常值对回归效果的影响，本文采用3σ准则对异常值进行检测和剔除［14～15］，具体步骤如下：

1）对位置数据值进行线性回归处理，由式（4）和式（5）计算得到a和b。

2）使用贝塞尔公式，即式（6）计算该组数据的标准差s：

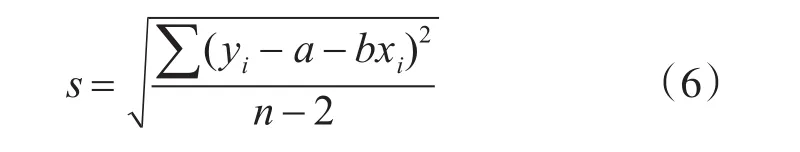
3）使用3σ准则，即式（7）对每组位置数据进行判断。如式（7）成立，则待检测的yi为异常值予以剔除。

4）对余下的位置数据重复步骤1）、2）和3），直至剔除所有异常值，最后由式（4）和式（5）求解得到直线的轨迹方程。

2.4 基于折线交点的RSSI值多项式模型

如图2所示，I点为直线轨迹L1和L2的交点，A点和B点为L1与未知节点通信区域的交点，C点为未知节点U在直线L1上的垂点。将交点I作为参考节点，直线轨迹上的其他点与交点间的距离作为相对距离。由RSSI值模型可知，距离未知节点越近的地方，信号强度越强，锚节点从A点经C点运动至B点的过程中时，未知节点获取到的RSSI值变化趋势如图3示。

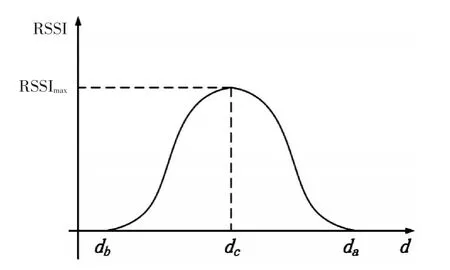
图3 RSSI与相对距离d的关系图

为求解出轨迹L1最大值RSSI值点处的相对距离dC，本文采用文献［8］的方法，分别对轨迹AC和轨迹CB段的RSSI值和相对距离d进行曲线拟合，可以得到以相对距离d为自变量的拟合方程（8）和式（9）［8］：

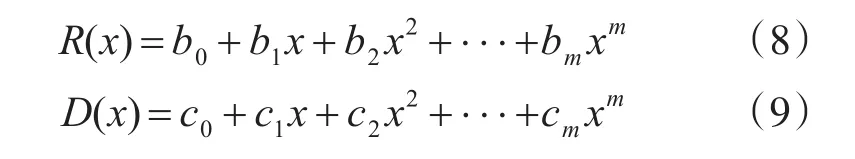
其中，R（x）和D（x）分别直线段轨迹AC和CB段的RSSI值多项式方程，联立式（10）和式（11）求交点，由式（12）可求解得到L1直线段轨迹上最大RSSI值处的相对距离dC：

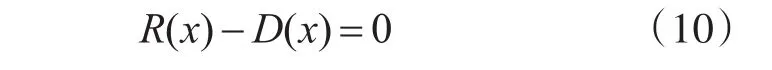
同理可以求解得到直线轨迹L2上最大RSSI值处的相对距离。

2.5 基于最大RSSI值的定位模型

同一平面内，过直线上或直线外的一点，有且只有一条直线和已知直线垂直。未知节点获得两条不同直线轨迹上的最大RSSI值点的位置坐标，求解得到过该点且垂直于直线轨迹的垂线，两垂线的交点即为所求的未知节点。

如图 4所示，点C1(cx1，cy1)，C2(cx2，cy2)分别为锚节点直线轨迹L1和L2上的最大RSSI点；L3和L4分别U在L1和L2上的垂线。分别对直线轨迹L1和L2进行线性回归处理得到对应的方程式（11）和式（12）：

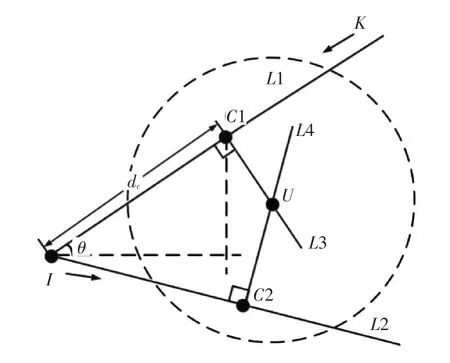
图4 最大RSSI值的定位模型图

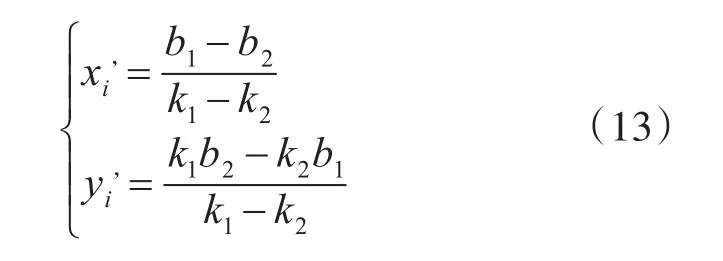
直线L3，L4分别垂直L1，L2，由几何关系可得L3和L4的方程分别为

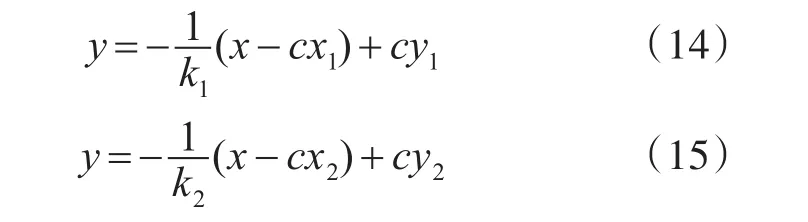
由式（14）和式（15）可求解得未知节点U的坐标：

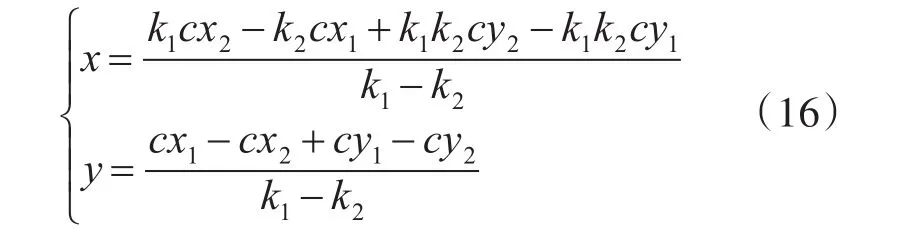
(cx1，cy1)和 (cx2，cy2)分别为垂点C1和C2的坐标，由图4可知垂点坐标：

其中，θ=arc(tank)，联立式（4）、式（5）、式（13）、式（16）和式（17）可解得未知节点的坐标。对未知节点的坐标公式分析可以得知：

1）由式（4）、式（5）、式（13）、式（16）和式（17）的推导过程可知，未知节点坐标的解算精度最终受到锚节点的位置误差和位置数据样本量n的影响。

2）k1≠k2，即执行折线运动过程中，两条直线段不能重合或者平行，否则将导致算法无解。

3 仿真实验

为验证GNSS系统的定位误差和位置数据集的样本量n对未知节点坐标解算的影响，本文采用Matlab软件对算法进行了仿真分析，仿真参数设置如下：Pt=1W，η取值为1，Xσ的标准差取值为5。

无线传感器网络的场景设定如下：在40m*40m的矩形监测区域内，随机布放10个固定节点，锚节点规划路径在监测区域内运动。为保证仿真结果的准确性，将10次独立仿真结果的平均值作为最终结果。分别采用本文的算法、文献［7］和文献［8］的算法进行比较。相关的仿真结果如图5和图6所示。

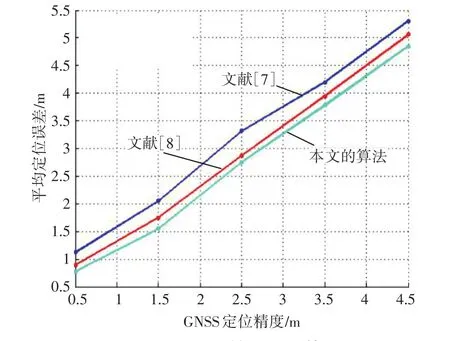
图5 GNSS定位精度对解算影响

图6 位置数据样本量n对解算精度影响

从图5可以看出，在相同的GNSS定位误差下，本文的算法明显高于其他两种算法，这是因为首先本文的算法引入了3σ准则对位置数据集中的异常值进行剔除，其次，构建了直线轨迹方程求解模型和RSSI值多项式模型有效降低了GNSS定位误差对后续求解的影响。第三，与原方法简单的采用轨迹上某一位置点作为参考节点相比，本文采用折线交点作为参考节点较原算法更为精确，拟合得到的RSSI方程也较原算法更符合理论值。因此本文算法的定位精度较其他两种算法得到了明显的提升。

由图6可知，样本量n的增加，三种算法的定位误差呈现出逐渐减小的趋势。这是因为在相同的测量条件下，测量次数越多，越能减小随机误差对测量数据的影响［13］。在相同的位置数据集样本量n下，本文的算法误差明显小于其他两种算法，证明本文采用的异常值剔除方法和两次回归拟合运算有效减小了异常值和GNSS定位偏差对未知节点坐标解算的影响。

4 结语

本文提出了一种改进的无线传感器网络节点定位算法，该算法最低只需要一个锚节点就能实现未知节点的定位，算法无需附加额外的硬件设备，使用成本低廉；构建的直线轨迹求解模型和RSSI值多项式模型简单易于实现；仿真实验表明：与原算法相比本文的方法有效减小了锚节点GNSS系统的定位数据误差对未知节点坐标解算的影响，具备较高的应用价值。